基于粒子群优化的同步风力发电机励磁系统的变论域模糊控制*

张 翔，董海鹰

(兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

0 引言

随着我国风电并网容量逐年增大，大规模风电场并网对电力系统稳定性有着直接影响［1］。电压控制对于提高电力系统的稳定性、维持系统电压平衡和传输损耗最小化具有重要意义［2］。当风电机组受到风速变化所带来的输入功率扰动以及电力系统发生故障时，会对风电机组的输出电压造成影响，为了保持风力发电机输出电压稳定，维持电力系统电压平衡，需要进行电压控制。

常规的双馈异步风力发电机和永磁直驱同步风力发电机采用后端恒频技术控制其输出电压［3］。双馈发电机通过双向励磁变频器调节转子绕组励磁电流来实现变速恒频控制［4］，而永磁同步发电机通过变流器对输出电压进行变频变压之后并网［5］，以上两种机组存在低电压穿越能力差、无功输出能力不足、电能质量等问题，很难满足我国对大规模风电并网越来越高的并网要求。前端调速式风电机组采用液力变矩前端调速系统实现了电励磁同步发电机的直接并网，其输出电压的控制通过励磁控制实现，因此具有低电压穿越和无功输出能力强、电能品质好等优点，从根本上提高了风电机组机并网运行的稳定性和可靠性［6］。

由于励磁系统的非线性、时变性，常规的励磁控制器已经难以满足越来越高的控制要求。变论域模糊控制具有不依赖于控制对象的精确数学模型，模糊论域可调等特点，将其应用于同步风力发电机励磁控制可获得良好动静态品质和鲁棒性。本文针对励磁系统的结构建立了机组励磁控制模型，设计了基于粒子群优化的变论域模糊励磁控制器。

1 系统模型的建立

1．1 同步风力发电机励磁系统结构

本文研究的同步风力发电机采用的无刷励磁系统如图1所示。

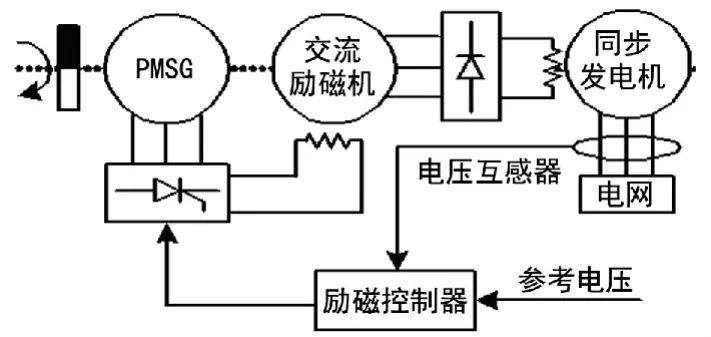
图1 励磁系统结构图

该励磁系统采用三级无刷励磁技术，由发电机、主励磁机、副励磁机组成。主励磁机是旋转电枢式同步发电机，副励磁机是永磁同步三相交流发电机。由于结构上省去了电刷和滑环，有效提高了励磁系统运行的可靠性。

励磁机的输出经不可控整流器供电给发电机励磁绕组，而励磁机的励磁由副励磁机经可控整流器提供，通过励磁控制器控制主励磁机励磁电流大小，调节发电机输出电压。

1．2 励磁系统数学模型

为了简化数学模型，采用IEEE AC－1型无刷励磁系统模型［7］，该模型考虑了励磁机的去磁反应、饱和效应以及不可控整流桥的换相压降等因素的影响，可以反映出励磁系统的动态过程。AC－1型无刷励磁系统结构框图如图2所示。

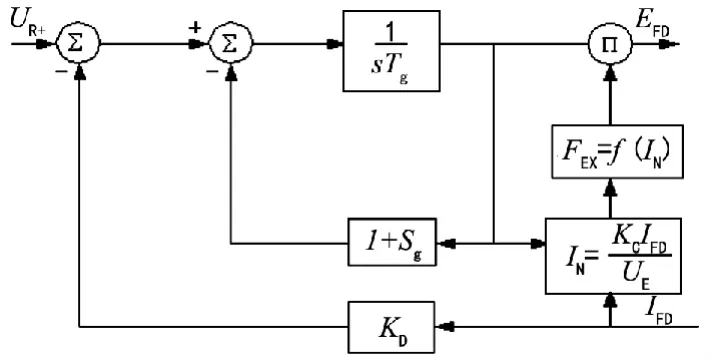
图2 无刷励磁系统结构框图

无刷励磁系统的数学模型为:

式中:UFD为发电机的励磁绕组电压;UE为励磁机的电枢电压;FEX为整流器的整流系数;SE为励磁机空载饱和系数;KD为励磁机的电枢反应系数。

2 励磁控制结构

本文设计的同步风力发电机励磁控制系统如图3所示。

图3 同步风力发电机励磁系统控制框图

无刷励磁系统采用双闭环控制，外环为电压环，电压的反馈是发电机的电压通过电压传感器测量得到的，该环的控制器是基于粒子群优化的变论域模糊控制器。通过控制器之后，得到电流环的给定值，通过限制器之后进入电流控制内环，电流内环的反馈是通过传感器将交流励磁机的励磁绕组电流测量得到的。通过电流环的控制作用，最终获得对交流励磁机的控制作用，同时，电流环的反馈也将交流励磁机的时间常数得以补偿。

3 变论域模糊控制

3．1 变论域理论

常规的模糊控制中，论域确定之后固定不变，无法根据输入误差的变化调整模糊论域，导致控制精度不高。文献［8］中首次提出了变论域思想:在模糊控制规则形式不变的前提下，通过选取合适的论域伸缩因子，使得模糊控制器的初始论域随着误差变小而收缩，或随着误差增大而扩展。局部地看，论域收缩相当于论域中的模糊集合的划分更加细密，相对性的增加模糊语言变量值及控制规则，能够更精确地逼近理想控制函数，从而达到提高控制精度的目的。

设输入变量xi(i=1，2，···，n)的基本论域为Xi=［－E，E］(i=1，2，···，n)，输出变量y的基本论域为Y=［－U，U］，{Aij}(1≤j≤m)为论域Xi上的模糊划分，{Bj}(1≤j≤n)为论域Y上的模糊划分，则有模糊规则:

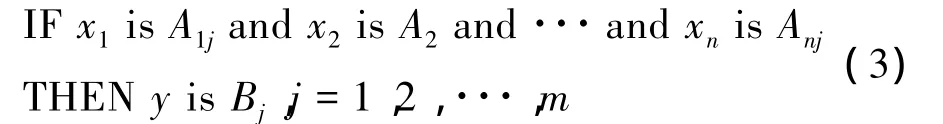
设xi，yj分别为Aij，Bj的峰点值。变论域理论是指论域Xi与Y可以分别随着变量xi与y的变化而变化。记为:

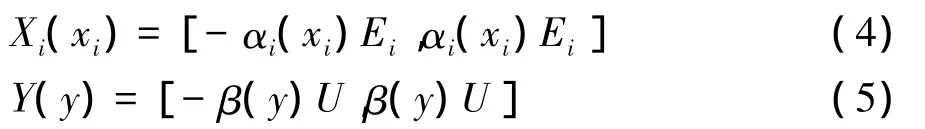
式中:αi(xi)(i=1，2，···，n)与β(y)为相应论域的伸缩因子。变论域示意图如图4所示。

图4 变论域示意图

3．2 变论域伸缩因子

在变论域模糊控制器的设计过程中，因为系统需要根据伸缩因子的变化来提高控制的精度。伸缩因子可定义为根据当前控制指标值实现对各语言控制变量论域的调整。对于伸缩因子α(x)函数，应该满足如下条件。

(1)α(0)=0

(2)α在［0，E］范围上严格单调递增。

(3)∀x∈X，满足 α(x)= α(－x)。

(4)α(±E)=1

(5)∀x∈X，有|x|≤α(x)E 成立。

对于本文的双输入单输出模糊控制系统，输入变量X与Y通常是互相关联的，一般取X为误差e的论域，Y为误差变化率ec的论域。因此，β(y)应定义在X×Y上，即β=β(x，y)。本文选择构造比例指数型伸缩因子结构［13］如下:

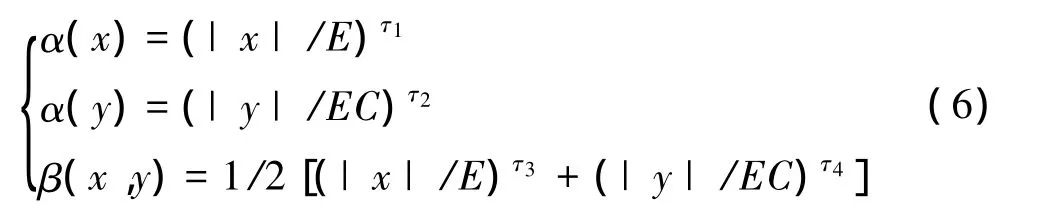
式中:τ1，τ2，τ3，τ4为待优化参数。

3．3 基于粒子群优化的变论域模糊控制器设计

为了便于变论域模糊控制器的实现，基于粒子群算法的变论域模糊控制器将采用以输入伸缩因子α1(e，ec)和α2(e，ec)分别除以输入变量 e、ec，输出伸缩因子β(e，ec)乘以输出变量u的方式实现控制器结构。基于粒子群优化的变论域模糊控制结构如图5所示。

图5 粒子群优化的变论域模糊控制结构

数学表达式为:

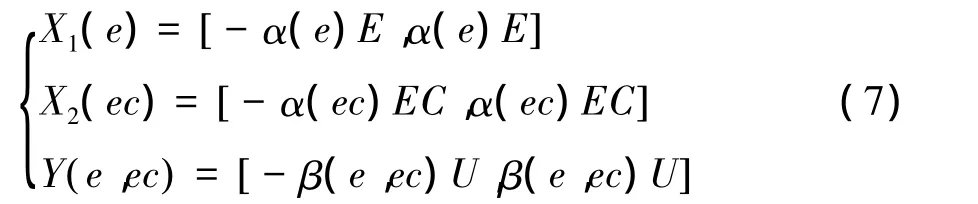
式中:α(e)、α(ec)和 β(e，ec)为论域的伸缩因子，e、ec是时间函数。

将 PSO 算法作为伸缩因子结构参数 τ1，τ2，τ3，τ4的寻优算法，以此构成变论域模糊控制器。

算法流程:

(1)设粒子的维数 D=4，待寻优参数 θ=［τ1，τ2，τ3，τ4］，参数变化范围(0，1)，种群规模 N=20，迭代次数100次，进行粒子的位置和速度初始化，赋值给伸缩因子。

(2)根据ITAE最佳性能指标，以电压误差和时间乘积的积分建立PSO算法的适应度函数，用J表示粒子当前的适应度，J越小适应度越高。

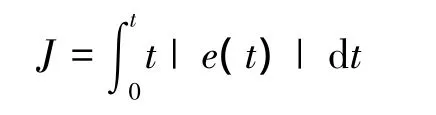
(3)计算每个粒子的适应度值，进行粒子的状态更新，根据式(8)进行粒子的速度和位置更新。

(4)PSO算法基于此适应度函数，更新粒子状态在每个采样周期内对伸缩因子的参数进行寻优，寻优求得最优解后，将其输出作为下个采样时刻变论域模糊控制器的伸缩因子的参数。

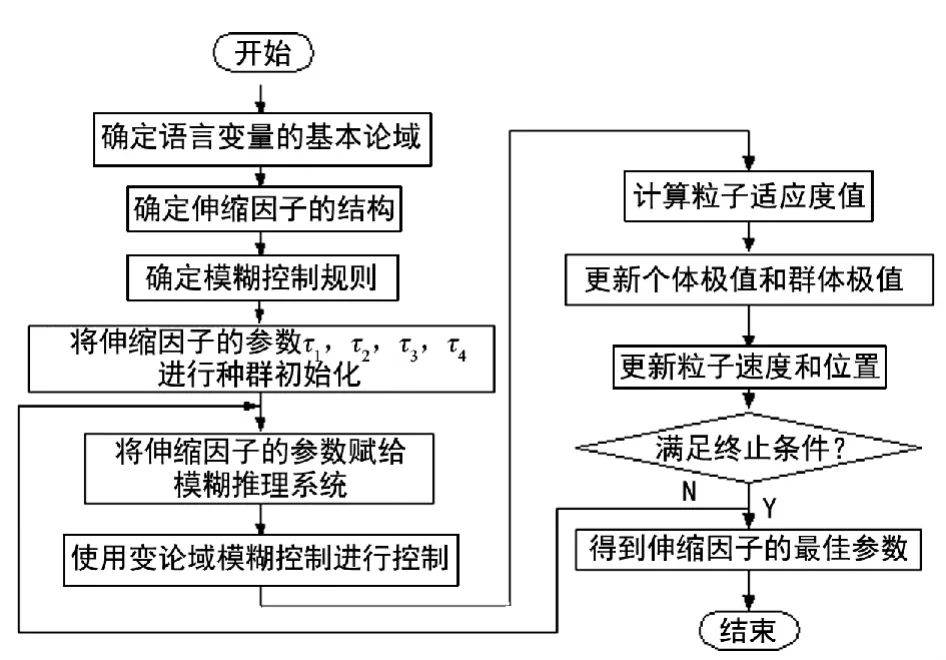
图6 基于粒子群优化的变论域模糊控制流程图

(5)经过设定的迭代次数后，算法收敛于最优解，输出最优解作为伸缩因子最优参数，从而实现粒子群优化的变论域模糊励磁控制。粒子群优化伸缩因子参数的算法流程如图6所示。

4 仿真分析

基于matlab/simulink仿真软件，建立单机无穷大系统仿真模型。

同步发电机参数为:额定功率2 MW，额定电压690 V，额定转速1 500 r/min。结构参数如表1所示。

表1 同步发电机参数表

励磁系统参数为:C1=0．158，C2=0．00248，TE=1．15，KE=1．15，KD=0．96，Kc=0．215。

4．1 输入功率扰动

额定风速以下，发电机保持稳定运行，在1 s时，风速达到额定风速，发电机输入功率上调20%达到额定功率时，系统有关状态量U、P和ω的响应曲线如图7所示。

图7 输入功率变化时发电机各状态量响应曲线

表2 两种控制方法性能指标对照表

图7(a)表明当输入功率扰动时，采用粒子群优化的变论域模糊励磁控制的同步发电机输出电压能迅速恢复稳定，而常规的模糊控制振荡次数多，恢复时间长。图7(b)表明本文的励磁控制方法与常规模糊控制相比，振荡次数少，收敛速度快，使得发电机有功功率具有良好的跟踪特性。图7(c)表明发电机转子转速只发生了轻微的超调。表2给出了两种不同控制方法下，对于电压的控制性能指标。

4．2 三相短路扰动

在1s时，发电机输出线变压器高压侧设置三相短路故障，持续时间0．1 s，系统有关状态量U、P和ω的响应曲线如图8所示。

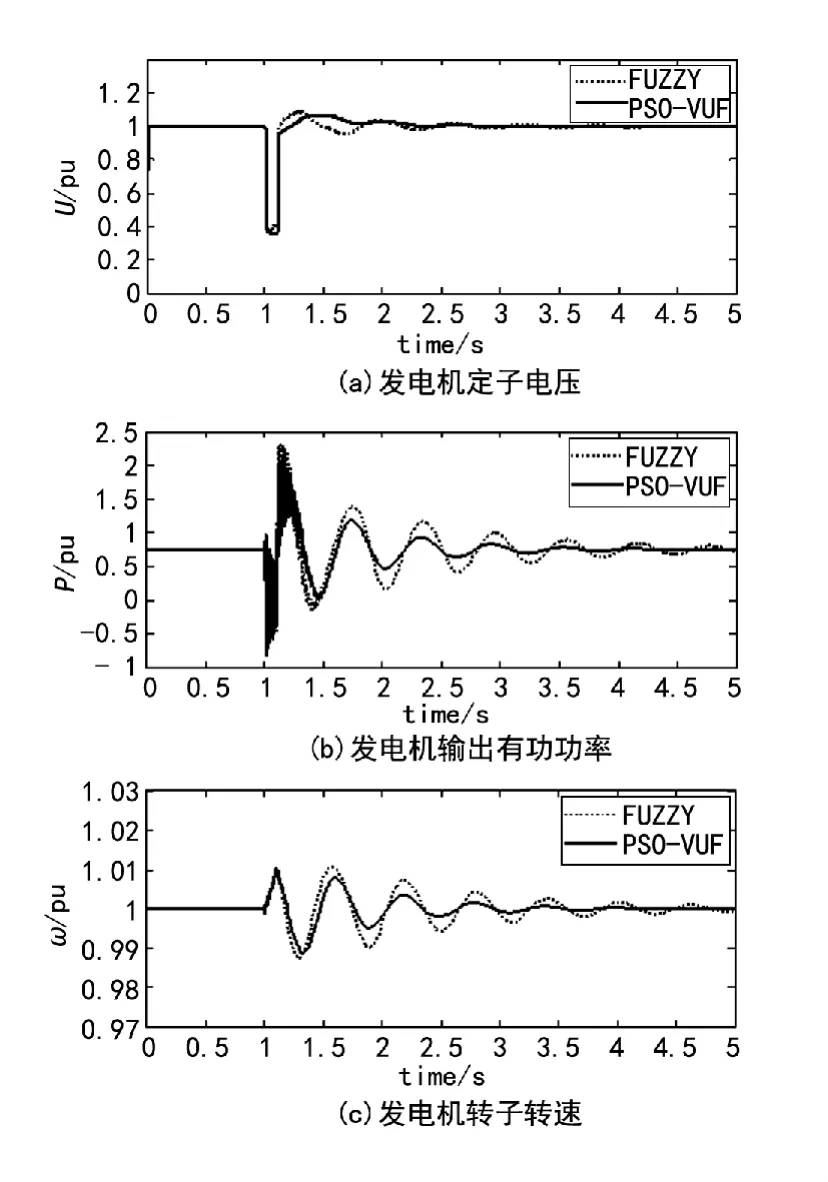
图8 三相短路故障时发电机各状态量的响应曲线

表3 两种控制方法性能指标对照表

图8表明，当电力系统发生三相短路故障时，两种控制方法均能使系统返回初始平衡运行点，但采用粒子群优化的变论域模糊励磁控制能较好的抑制暂态过程中的机械振荡，使发电机具有良好的动、静态性能。从图8(a)可以看出，当短路故障切除后，本文的励磁控制方法可以迅速将电压恢复到给定值，满足了电压调节精度的要求。图8(b)表明在系统发生故障时，发电机输出有功功率振荡小，可以迅速恢复到稳定状态。图8(c)表明该方法可以有效的抑制发电机的转子振荡。表3给出了两种不同控制方法下，对于电压的控制性能指标。

5 结论

针对同步风力发电机励磁系统的精确模型难以获取、励磁参数时变的特点，设计了基于粒子群优化的变论域模糊励磁控制器，该控制器将粒子群优化算法与变论域模糊控制相结合，实现了模糊论域的自调整，以满足不同工况对控制参数的不同要求，改善了传统控制方法在系统运行状态改变或系统结构变化时适应性较差的不足。仿真结果表明，与常规的模糊控制相比，当风电机组运行工况发生改变时，该控制器可以有效的提高发电机端电压的调节精度，抑制发电机转子低频振荡，迅速将发电机从暂态过程中恢复至稳定运行平衡点，在稳定运行时具有较高的电压调节精度，动态过程中又能明显的提高系统阻尼特性，有效地解决了系统的暂态稳定性和发电机的端电压调节精度之间的矛盾。验证了该方法的有效性。

［1］ 刘 取．电力系统稳定及发电机励磁［M］．北京:中国电力出版社，2007．

［2］ Prabha Kundur，Neal J．Balu．Power System Stability and Control［M］．New York:McGraw－Hill Professional，Inc．．1994．

［3］ 曹 娜，赵海翔，戴慧珠．常用风电机组并网运行时的无功与电压分析［J］．电网技术，2006，30(22):91－94．

［4］ 林成武，王凤翔，姚兴佳．变速恒频双馈风力发电机励磁控制技术研究［J］．中国电机工程学报，2003(11):126－129．

［5］ 姚 骏，廖 勇，庄 凯．永磁直驱风电机组的双PWM变换器协调控制策略［J］．电力系统自动化，2008(20):88－92．

［6］ Andreas Besteck．WinDrive－variable Speed Wind Turbines without Converterwith Synchronous Generator［R］．2009．

［7］ 李基成．现代同步发电机励磁系统设计及应用［M］．北京:中国电力出版社，2009

［8］ 李洪兴．Fuzzy的本质与一类高精度Fuzzy控制器的设计［J］．控制理论与应用，1997，14(6):868－872．

［9］ Liu X Y，Li L F，Chen W F．A Variable Universe Fuzzy Control Algorithm Based on Fuzzy Inference［J］．Proceedingsof the International Conference on Wavelet Analysis and Pattern Recognition，2007，20(5):453－457．

［10］ Li H X．Fuzzy variable structure control［J］．IEEE Trans on System，Man，and Cybernetics，1997，27(2):306－312．

［11］ 李洪兴，苗志宏，王加银．四级倒立摆的变论域自适应模糊控制［J］．中国科学(E 辑)，2002，32(1):65－75．

［12］ 李洪兴，苗志宏，王加银．非线性系统的变论域稳定自适应模糊控制［J］．中国科学，2002，32(2):211－223．

［13］ 李洪兴．变论域自适应模糊控制器［J］．中国科学(E辑)，1999，29(1):32－42．

［14］ 李洪兴．模糊控制的插值机理［J］．中国科学(E辑)，1998，28(3):259－267．

［15］ 潘湘飞，宋立忠．几种变论域模糊控制收缩因子有效性研究［J］．控制工程，2008，15(1):106－108．

［16］ 彭灵志，贺建军．基于粒子群算法的变论域模糊控制策略［J］．控制工程，2012(S1):116－118．