基于费效模型的单元重构及优化*

周建伟，李 翔，张雪丽

(兰州交通大学机电工程学院，甘肃兰州 730070)

0 引言

当产品的品种和批量发生变化时，如何在原有的制造环境中通过适当的调整和规划形成一个新的制造系统，来满足产品多样化的要求，是当今制造企业所面临的一个重要问题。可重构制造系统正是在这种需求下应运而生的，Koren Y教授首先较全面的提出了可重构制造系统的概念［1］。国内外学者先后对可重构制造系统的组成、特点、功能等方面进行了一定的研究。Tang Li进行了基于零件族的可重构制造系统组态设计与重构方面的研究。Faisal Hasan等对涉及多个零件族的可重构制造系统服务水平的性能指标进行了研究，窦建平等依据图论的方法对单件产品单生产线下的可重构制造系统进行了研究，Deif Ahmed从可重构能力和重构成本的角度对可重构制造系统组态布局进行了相关研究，Paolo Renna对可重构制造系统的产能重新配置与管理进行了研究［2-6］。可重构制造单元作为可重构制造系统的重要组成部分，它的性能好坏对制造生产有着极其重要的影响。

目前有许多制造单元构建规划模型被提出，但大多都是针对单一品种或单一路径下规划模型［7-9］，而实际生产中可能会面临多品种、多加工路径的问题，因此具有可实施性的制造单元应该考虑多种因素共同作用的结果，笔者综合考虑多个工件的加工批量、单位加工时间、单位加工成本、单位运输时间;不同路径下工件的加工工艺流程、单元间的运输成本等因素，以加工成本和运输成本最小化为目标，研究多制造单元构成的制造系统在多品种多路径制造环境下制造单元的优化组合问题。

1 费效模型构建

1．1 基本参数说明

P:设备总数;i:设备 i=1，2，…P;M:工件种类总数;Nn:工件n的数量;Nnr:工件n在路径r上的数量;Rn:工件n可能采用的加工路径数;r:路径;Cmax:单元总数;c:单元;Snr:工件n选用r加工路径时所采用的设备集合;Nc:单元内允许的最大设备数;AnrSnri:工件n采用第r条加工路径时在制造设备Snri上的单位加工成本;QnrSnri:工件n采用第r条加工路径时在制造设备Snri、Snr(i+1)间的单位运输成本;γ:单元间的单位运输费用;EnrSnri:工件n采用第r条加工路径时在制造设备Snri上的单位加工时间;GnrSnri:件n采用第r条加工路径时在制造设备Snri、Snr(i+1)间的单位运输时间;YnrSnri:设备Snri是否在单元c内，若在为1，否则为0;Dcl:单元 c与 l的单位运输时间;α(YSniic，YSnr(i+1)l):当 c=l时，说明设备 Snri、Snr(i+1)在同一制造单元内其值为0，否则为1;Vnr:零件n选择路径r其值为1，否则为0;Znc:零件n在单元c内其值为1，否则为0;Vic:设备i在单元c内其值为1，否则为0。

1．2 数学模型构建

目标函数:

min Z=αF1+βF2+γF3

其中，零件的加工成本为:

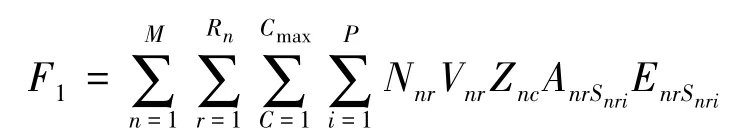
单元内运输成本:

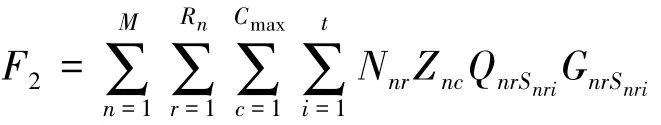
单元间运输成本:

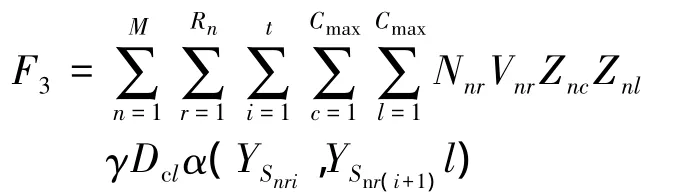
其中:α+β+γ=1

约束条件:

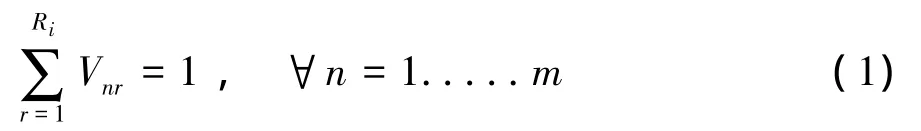
零件n只能选择一条加工路径。

判断零件n是否在单元c内，是为1否则为0。

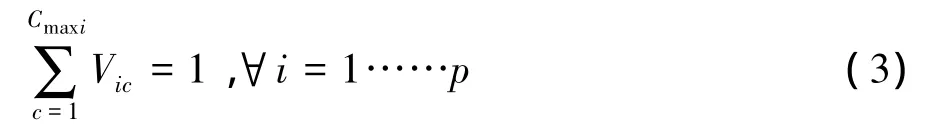
设备i只能分配到一个单元内。

单元c内的设备数不能超过总的设备数。

零件n在路径r上的数量不能超过零件n的总数。

浅议消费主义视阈下的大众传播效果——以电视节目《女神的新衣》为例 ………………………………………… 叶翰宸（1/61）

上述模型综合考虑单元构建和工件路径选择情况下，使得总加工成本和运输成本最低。

2 自适应遗传算法

目前有许多求解单元构建模型的方法，如粒子群优化算法、模拟退火算法、神经网络算法等［9-11］。遗传算法(Genetic Algorithm，GA)是一种基于自然进化和自然遗传原理的全局优化算法，相比于传统的优化算法，遗传算法具有较好的全局搜索性能，它能同时对多个可行解进行检查，使得搜索向更有可能找到全局最优解的方向进行。采用精英保留策略以及自适应算法来求解，即加快了求解速度，又保证求解不容易陷入局部最优解。

2．1 染色体编码

采用实数编码可以消除基因因编码精度不够，使得搜索空间中具有较优适应值的可能解未能表示出来的隐患［12］。遗传算法用实数编码的基因，具备了利用连续变量函数具有的渐变性的能力。因此，变量Vnr、Vic采用整数编码方式，如图1所示。

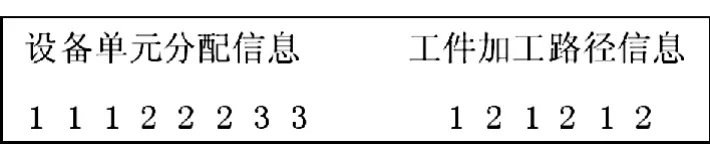
图1 染色体编码

设备单元分配的编码中数字表示所隶属的单元编号，比如第二个1表示设备2在第1个单元;工件加工路径编码表示每个工件有两条可选路径，比如第3个1表示工件3选择第一条加工路径。

2．2 适应度函数

通常优化问题中一般求目标函数f(X)的最小值，而不是最大值。遗传算法中要对个体适应度比较排序确定选择概率，所以适应度函数的值要求取正。一般将目标函数映射成求最大值形式且函数值非负的适应度函数。

一般情况下将一个最小化问题转化为最大化问题只需要把费用函数乘以-1即可。然而在遗传算法中这种方法还不足以保证适应度函数F(X)的非负性。通过以下方法进行转换:，若，其他式中:Cmax可以是一个合适的输入值，也可以是f(X)的最大值。

2．3 算子设计

(1)选择算子 选择算子是根据群体中对个体的适应度评估，按照优胜劣汰的选择方式，选取个体并遗传到下一代中的操作，适应度较高的被选中的概率大，适应度较小的被选中的概率小。通过选择操作可以避免基因缺失，提高全局收敛性和计算效率。选用赌轮选择的方法对选择算子进行操作。赌轮选择也叫适应度比例选择法或者蒙特卡罗选择。赌轮选择个体被选中的概率与其适应度的大小成正比。

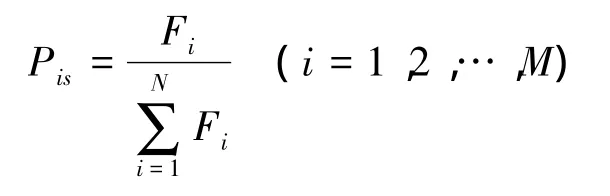
(2)交叉算子 交叉算子是遗传算法中产生新个体的主要方法，它的操作是对两个相互配对的染色体按照某种方式相互交换其部分基因，从而形成两个新个体。采用两点交叉对染色体进行操作。如图2。

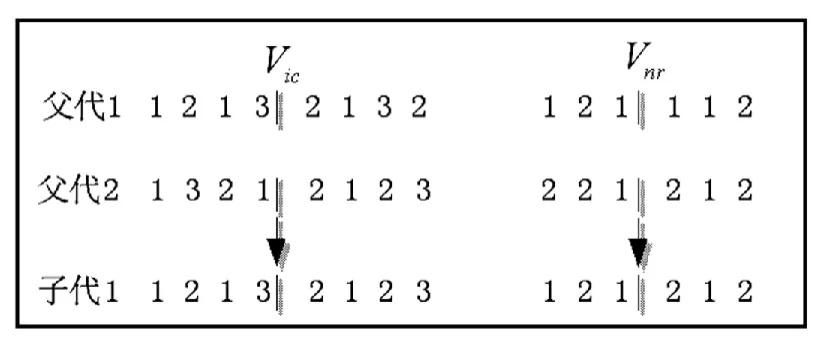
图2 染色体交叉

(3)变异算子 变异算子的基本操作是对群体中的个体编码串的某些基因位置上的基因值作变动。采用单点随机点变异方式进行变异。

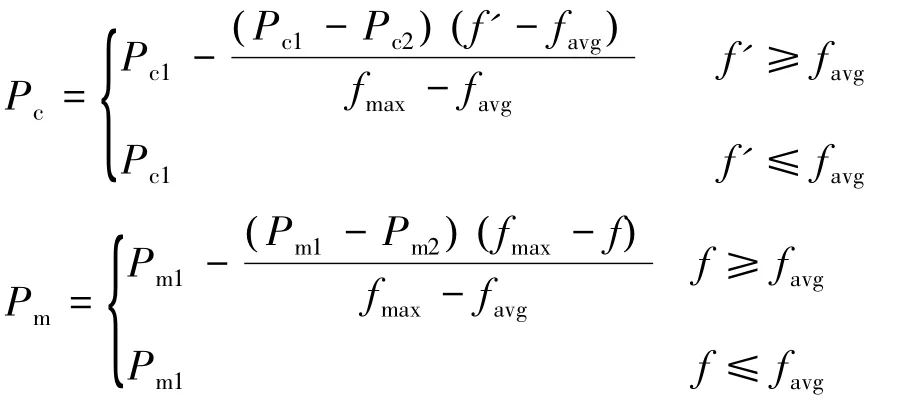
(4)自适应算法 交叉和变异概率的自适应选择方法就是随着个体适应值的变化，适当的调整交叉和变异概率，交叉概率Pc和变异概率Pm按照以下公式自适应调整:式中:fmax为群体中的最大适应度值;favg为每代群体的平均适应度值;f'为待交叉两个个体中较大的适应度值;f为要变异个体的适应度值;Pc1=0．9;Pc2=0．6;Pm1=0．1;Pm2=0．01。

2．4 精英保留策略

精英策略就是从每次迭代完成后的父代个体和子代个体中选取适应度高的个体作为下一次迭代的父代。也就是将父代个体和子代个体进行适应度大小的排列，从中选取适应度高的个体，从而保证每次迭代完成后的群体均为最优群体，并将最优群体最为后代复制的基础。

3 算例分析

假设同一单元内机床间的运输成本不计。机床［m1，m2］、［m3，m4，m5］以及［m6，m7，m8］分别位于不同的制造单元。工件在它们之间的单位运输成本分别为30、40、60(见表1)。工件在机床间的运输时间如表2。各工件在不同路径下在各个机床的加工时间以及加工成本如表5。

上述问题是一个多品种、多加工路径问题。通过自适应遗传算法对该问题求解得出各工件选择的路径分别为2 2 1 1 2 1，存在4次跨单元加工，工件—设备单元划分如表4所列。经过加工运输成本的优化，制造单元间的加工成本和运输成本得到了明显的改善(见表3)，相比于完全在第一条路径加工下，优化后的加工成本降低了 13．9%，运输成本降低了31．9%，总成本降低了20．9%。

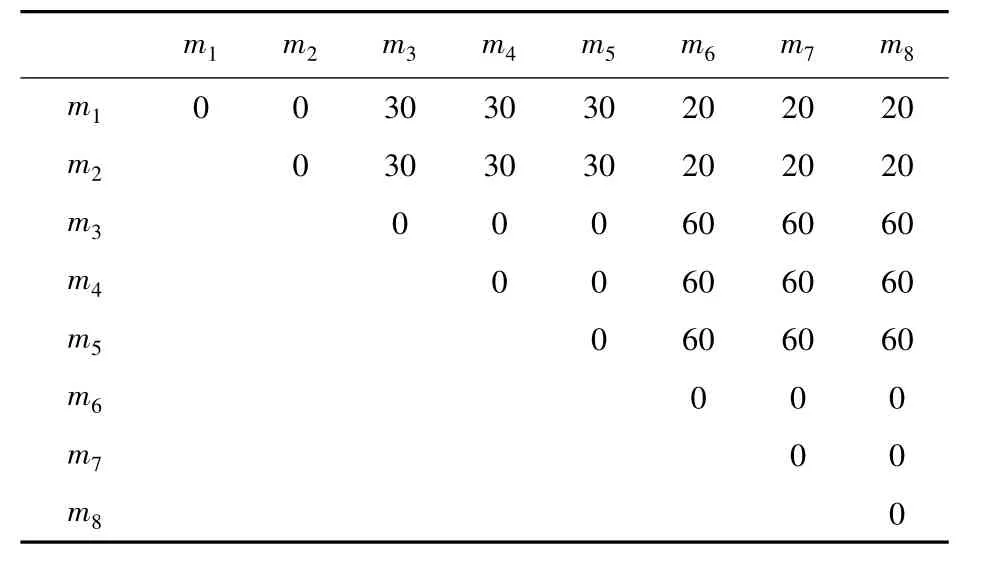
表1 工件在机床间的单位运输成本

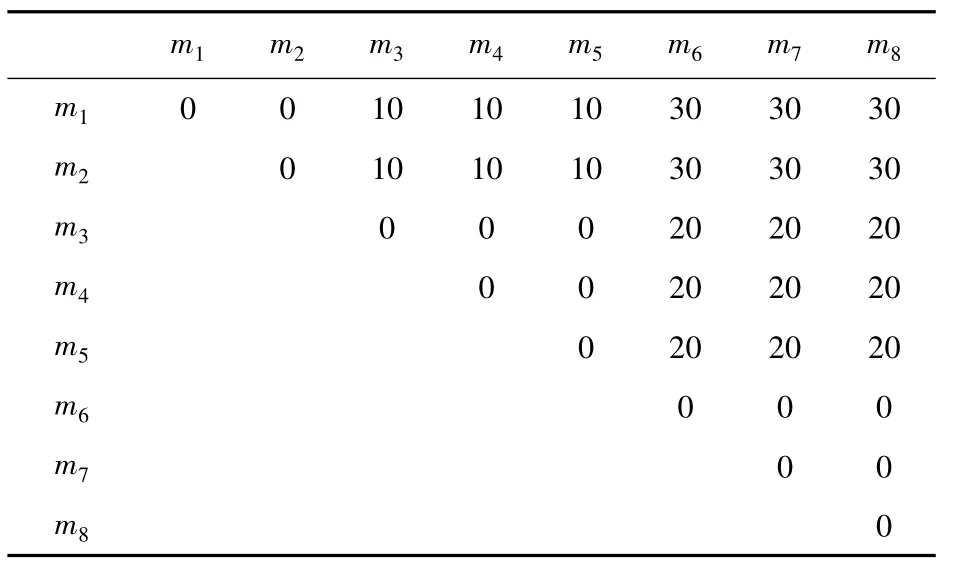
表2 工件在机床间的运输成本

表3 优化前后加工数据对比

表4 工件—设备单元划分

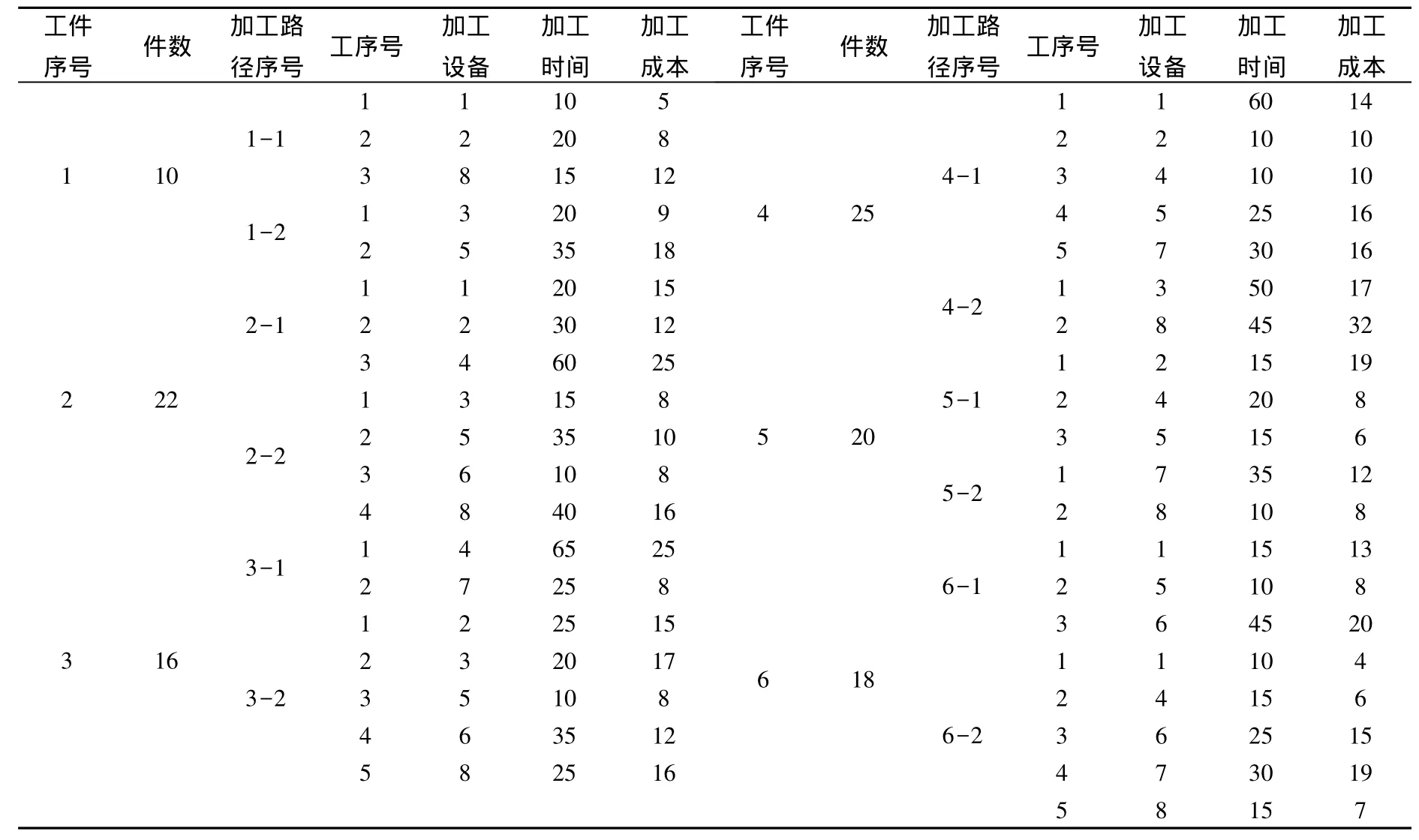
表5 加工数据

4 结语

随着客户对产品多样化、个性化需求的提高，许多企业必须由传统的大批量生产方式像小批量、多品种的生产方式转变。在此背景下，越来越多的生产制造系统以及生产制造方式被提出，并运用在生产实际中。可重构制造单元作为制造系统的重要组成部分，它的快速重组不仅能够快速响应市场需求的变化，而且兼顾了大批量生产的成本优势。

笔者主要考虑存在多条加工路径和操作顺序的情况下，使其加工和运输成本最低为目标的单元构建模型，为企业合理安排机器零件加工提供了一定的数学依据。没有考虑每台设备的加工能力以及机床间的运输成本，且是单周期下需求已知的情况下的数学模型，随着市场需求变化的复杂性，接下来的研究将进一步扩大到考虑设备加工能力以及多周期情况下需求变化的单元制造问题。

［1］ Koren Y，Heisel U，Jovane F，etal．Reconfigurable Manufacturing Systems［J］．Annals of CIRP，1999，48(2):527-540．

［2］ Tang li．Design and Reconfiguration of RMS for Part Family［D］．Michigan，USA:University of Michigan，2005．

［3］ Faisal Hasan，Pramod Kumar Jain，Dinesh Kumar．Service Level as Performance Index for Reconfigurable Manufacturing System Involving Multiple Part Families［J］．Procedia Engineering，2014(66):814-821．

［4］ Jianping Dou，Xianzhong Dai，Zhengda Meng．Graph Theory-based Approach to Optimize Single-product Flow-line Configurations of RMS［J］．The International Journal of Advanced Manufacturing Technology，2009(41):916-931．

［5］ Deif Ahmed，EIMaraghy Waguih．Investigating Optimal Capacity Scalability Scheduling in a Reconfigurable Manufacturing System［J］．International Journal of Advanced Manufacturing Technology，2007(32):557-562．

［6］ Paolo Renna．Capacity Reconfiguration Management in Reconfigurable Manufacturing Systems［J］．The International Journal of Advanced Manufacturing Technology，2010(46):395-404．

［7］ 付宜利，石旭东，何 霆，等．基于遗传算法的制造单元重组技术研究［J］．计算机工程与设计，2002，23(4):1-9．

［8］ 陈雄兵．可重构单元的构建及其评价研究［D］．重庆:重庆大学，2012．

［9］ 徐立云，荣 巨，郭昆吾，等．基于粒子群改进算法的制造单元构建方法研究［J］．制造技术与机床，2014(3):32-37．

［10］ F．Musharavati，A．M．S．Hamouda．Stimulated Annealing with Auxiliary knowledge for Process Planning Optimization in Reconfigurable Manufacturing［J］．Robotics and Computer-Integrated Manufacturing，2012(28):113-131．

［11］ 王国新，阎 艳，宁汝新，等．模糊神经网络与启发式算法相结合的制造单元构建方法［J］．计算机集成制造系统，2008(11):2175-2183．

［12］ 陈伦军．机械优化设计遗传算法［M］．北京:机械工业出版社，2005．