基于排队理论的制造单元构建与加工路径选择*

李 翔，周建伟，张雪丽，李忠学

(兰州交通大学机电工程学院，甘肃兰州 730070)

0 引言

单元制造是成组技术(GT)在制造领域中的一个重要应用。单元制造系统在减少加工成本与物料搬运成本、缩短任务期、实现集中管理等方面体现出很大的优势。目前单元制造系统的研究主要包括:单元构建、单元布局设计与单元管理三方面［1］。

设备组与零件族是单元构建的两个重要因素，针对单元构建问题，国内外学者提出了很多数学模型。用于构建单元的目标规划模型主要是基于成本最优原则［2-4］，划分的单元块与选定的工件加工路径能够保证较低的加工成本与物料搬运成本，但由于在建立模型时并没有考虑加工系统中存在的排队现象，会导致某种设备前有排队而某种设备却一直闲置的问题，这不仅会增加后续的设备维修费用，而且设备负荷强度不均衡则不能保证相近的零件加工进度，不但对企业是一种资源的浪费，也会增加生产管理难度。Buzacott等［5］提出用排队理论将具有相似加工时间的零件分配到同一单元，使单元便于生产管理。Arghis等［6］运用排队理论建立了减少闲置成本与等待成本的单目标规划数学模型。

笔者借鉴Buzacott和Arghis运用排队理论的建模方法，将每台设备看作是一个M/M/1排队系统，整个系统等效为一个开环排队网络模型。模型中的工件具有多种加工路径，优化加工成本与等待成本的同时，削弱排队影响、均衡设备服务强度与单元服务强度，最终实现单元构建与工件加工路径选择。

1 理论基础

1．1 排队基本原理

排队在生产实际中是一种常见的现象，例如车间中在机床边等待加工的零件。在排队理论中，把要求服务的对象统称为“顾客”，把提供服务的人或机构称为“服务台”。一个排队系统有3个基本组成部分:输入过程、排队规则和服务机构，本文中的排队系统采用M/M/1形式，即到达过程是泊松过程，服务时间服从负指数分布的单服务台排队系统［7］。在构建单元前，首先将多种设备组成的整个加工系统看作一个服务台，如图1所示，则整个系统构成一个M/M/1排队模型。假设存在i种零件，每种零件的到达率是λi，则对整个加工系统而言，零件的到达率是:

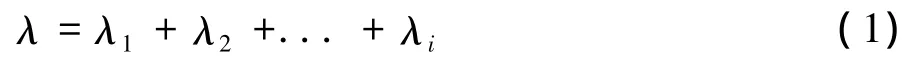
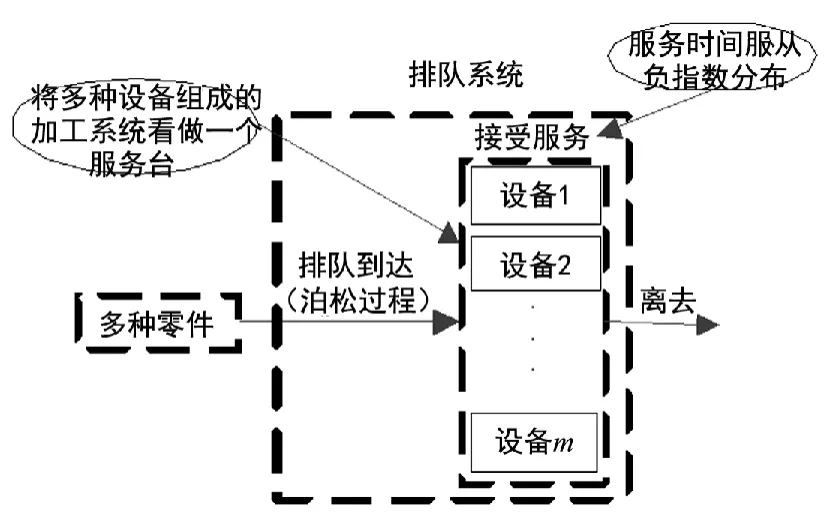
图1 系统排队模型

1．2 排队网络

一个排队网络是一些节点的集合，作业在这些节点间移动并接受服务。每一个节点从其本身而言都是一个排队系统。开环排队网络是指既有到达网络的顾客流又有向网络外部输出的顾客流。当把每一台设备看作是一个节点时，工件在一个节点接受服务后，可以离开网络或者去下一个节点继续接受服务，整个系统就构成一个Jackson开环网络模型［8］。

每个节点n的总体到达率λn是外部到达率λn'和网络内部到达率之和。对任意节点m=1，2，．．．，M，作业在节点m接受服务后到节点n继续接受服务的概率是pmn。根据定理:M/M/1队列的离去过程也是泊松过程，这个过程与到达过程相同［］。即离开节点m的离开率与到达率λm相等。因此有:

1．3 排队系统的经济分析

排队现象在加工制造系统中的存在是必然的，但以完全消除排队现象为研究目标是不合理的，这会造成设施的严重浪费。从经济成本角度考虑，排队系统中的费用包括服务费用与等待费用。前者是服务水平的递增函数，后者是服务水平的递减函数，如图2所示。文中优化的目标之一是使两者的费用之和最小，即:

式中:Cm是服务费用;Cw是等待费用。

图2 排队系统经济模型

2 数学模型

基于排队理论的单元构建模型满足下述假设条件:①工件与设备满足M/M/1排队模型的要求;②每种工件至少存在一种加工路径即r≥1，加工之前须指定特定的加工路径;③加工工序先后顺序不会对构建单元产生影响;④零件种类与设备种类已知;⑤在同一设备上完成不同工件的加工所需时间相同，且每种设备的服务率与单位时间运行费用已知;⑥设备前的单位时间等待费用有两种，分别是本单元内的工件排队时的单位时间等待费用与其它单元内的工件排队时的单位时间等待费用，两种费用均不受单元内与单元间布局形式的影响。

模型具体形式如下:

令:i为工件编号，i=1，2，．．．，P;j为设备编号，j=1，2，．．．，M;k 为单元编号，k=1，2，．．．，C;r为加工路径编号，r=1，2，．．．R;vj为设备 j的单位时间运转费用;μj为设备j单位时间内可完成的同类操作数目，即设备j的服务率;λj为工件到达设备j的到达率;λi为工件 i的到达率;ρj为设备 j的服务强度;ρk为单元k的服务强度;Wj为设备j前的平均等待时间;Wj'为工件在设备j的排队系统中的逗留时间;ν，ν'为设备前的两种单位时间等待费用，且 ν＜ν';αirj为工件i在路径r下是否需要设备j上加工，如果需要则αirj=1，反之为零;Mmax为一个单元内的最大设备数目;Mmin为一个单元内的最小设备数目;Pmax为一个单元内可加工的最多工件数;Pmin为一个单元内可加工的最少工件数;ρjmax为设备j的最大服务强度;ρjmin为设备j的最小服务强度;ρkmax为单元k的最大服务强度;ρkmin为单元k的最小服务强度。

决策变量:

xik:如果工件分配到单元k内，则xik=1，其它等于0。

yik:如果设备分配到单元k内，则yik=1，其它等于0。

zir:如果工件i选择路径r加工，则zir=1，其它等于0。

目标函数有:

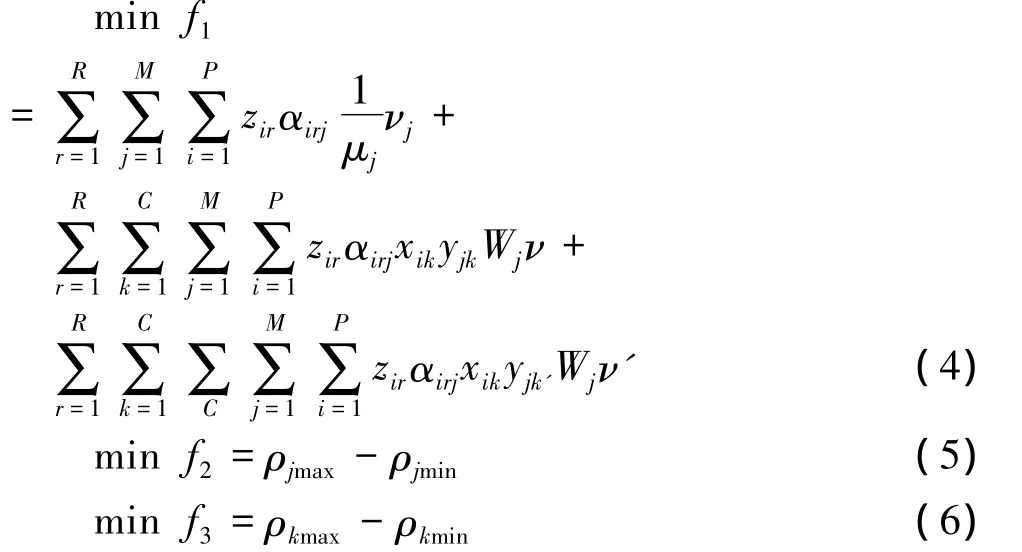
式(4)中，第一部分是工件的加工成本，第二部分与第三部分是排队费用，其中zirαirjxikyjk表示工件i与在加工路径r下需要的设备j在同一单元内，zirαirjxikyjk'表示工件i与在加工路径r下需要的设备j不在同一单元内。式(5)表示最小化设备服务强度范围，式(6)表示最小化单元服务强度范围。

约束:

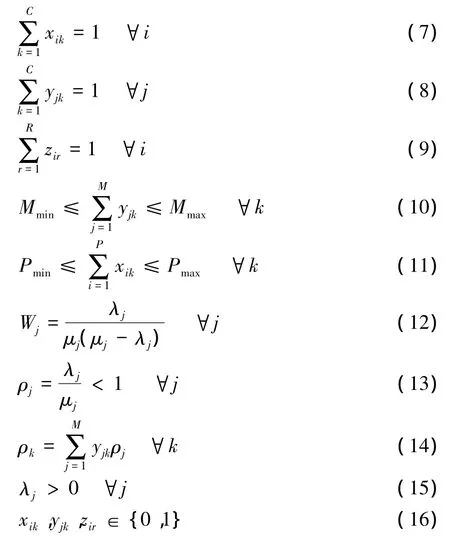
在上列约束中，式(7)和式(8)限制每种工件和设备只能属于唯一的单元;式(9)保证每种工件只能选择一种加工路径;式(10)表示单元大小限制;式(11)表示单元加工能力限制;式(12)计算任意设备前的排队时间，其中根据式(1)、(2)和假设(2)可得:

式(13)表示设备负荷强度约束;式(14)计算单元负荷强度;式(15)表示不能有设备始终闲置;式(16)决策变量域约束。

将三个目标函数利用线性加权和法构造成一个评价函数，多目标函数转化为单目标优化问题。加权因子分别为 ω1、ω2、ω3，构造的评价函数如下:

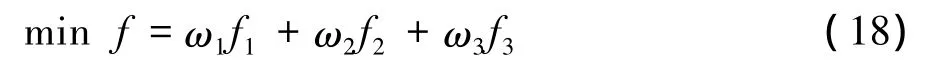
3 算例

为了检验上述模型的有效性，随机选择如下数据:有10种分别有两种加工路径的工件与10种设备，工件-设备原始矩阵如表1所列，表中前一列数据表示加工路径1，后一列数据表示加工路径2;工件的到达率如表2所列;设备服务率及单位时间运行费用如表3所列;设备前的两种单位时间等待费用分别取 ν=0．3，ν'=0．7。

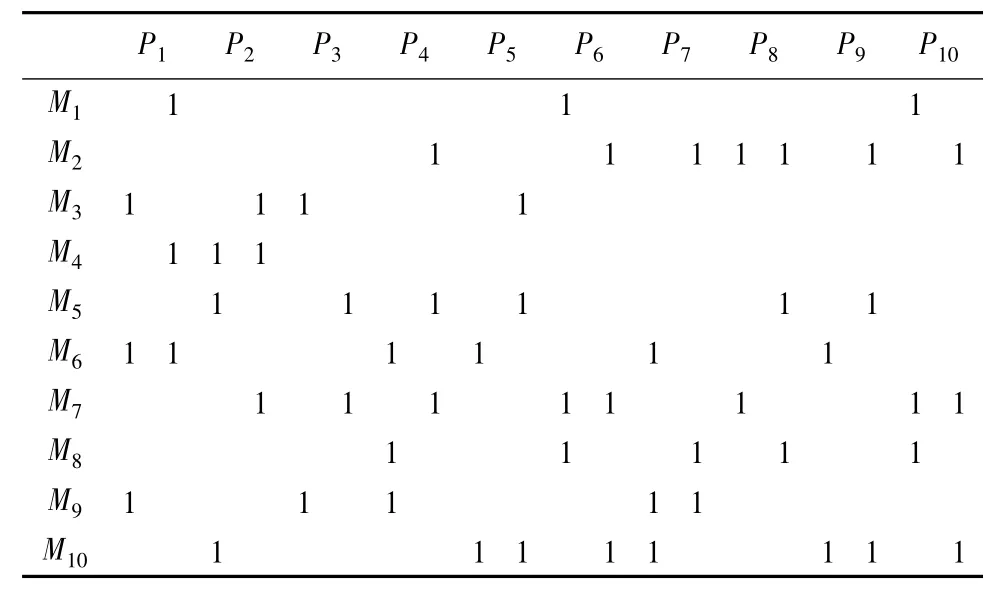
表1 设备-工件原始矩阵

表2 工件到达率

表3 设备服务率以及单位时间运转费用

参数设置:构建3个单元;单元大小限制为:Mmin=2，Mmax=4;单元加工能力限制为:Pmin=2，Pmax=4;加权因子分别取 ω1=0．5，ω2=0．4，ω3=0．1。笔者采用分枝定界法，在Lingo软件环境里对其编程仿真，可以得到一个Pareto解。

实验结果:评价函数值是3．451815;每台设备的 Wj、Wj'λj以及 ρj值如表 4;单元构建结果与路径选择结果如表5 所列，工件1、2、3、5、6、8、9 选择加工路径1，工件4、7、10选择加工路径2;单元服务强度如表6所列。

表 4 设备的 ρj、W j'、W j和 λj值

从图表4～6可看出，通过该模型能够较好的构建单元并选出加工路径。通过优化设备服务强度范围，工件通过系统的时间也得到了优化。单元服务强度与单元内的设备种类、设备服务率、工件种类、工件到达率等息息相关，通过模型优化，三个单元的服务强度也处于相近的范围内。针对这个算例，笔者通过改变单元数等相关等参数进行了多次求解，结果表明划分三个单元时评价函数值最小。

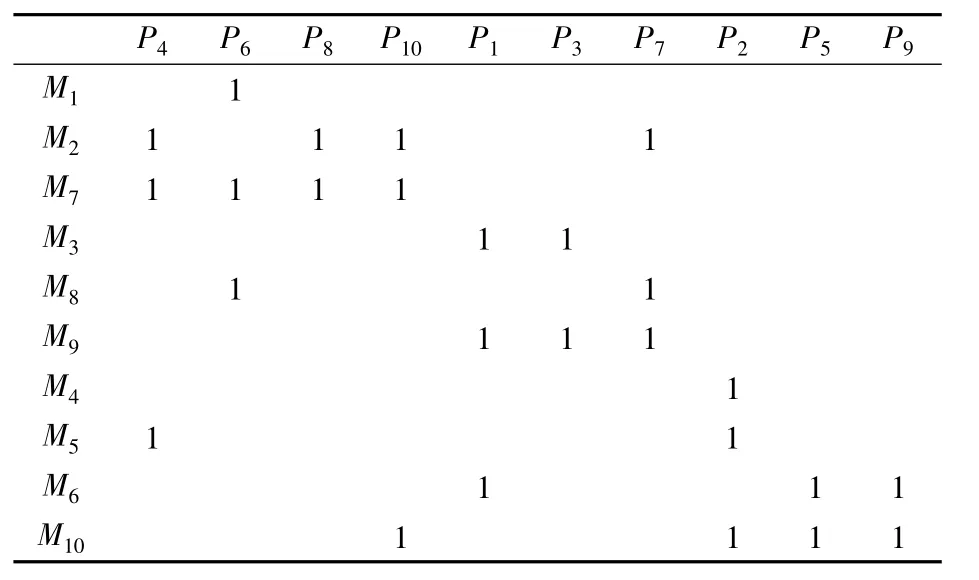
表5 单元构建结果矩阵

表6 单元服务强度

4 结语

研究了如何利用排队理论解决单元制造系统的单元构建与工件加工路径选择问题。构造了以最小化加工成本与等待成本、最小化设备与单元服务强度范围(设备、单元负荷均衡)为目标的多目标非线性0-1整数规划模型，采用线性加权和法将多目标问题转换为一个评价函数，模型求解用分枝定界法。最后在Lingo12平台上验证了一个随机算例，实验结果证明该模型能够实现单元构建、工件加工路径选择、优化设备服务强度与单元服务强度的目标，达到了预期效果。

笔者采用的排队基本模型是M/M/1形式，实际上当工件到达分布与设备服务时间分布是一般情形时，文中所建模型也同样适用。但是所建模型是基于不受单元内与单元间布局方式的影响假设，针对这个问题，如何完善模型并应用启发式算法求解大规模问题还有待深入。

［1］ 吴晓丹，王云峰，朱昭杰，等．单元制造系统集成建模研究［J］．计算机集成制造系统，2000，6(2):36-40．

［2］ Jabal AmeliM S，Moshref JavadiM．Concurrent Cell Formation and layout Design using Scatter ssearch［J］．International Journal of Advanced Technology，2014，71(1/4):1-22．

［3］ Raminfar R，Zulkifli N，Vasili M，etal．An Integrated Model of Production Planning and Cell Formation in Cellular Manufacturing Systems［J］．Journal of Applied Mathematics，2013:1-10．

［4］ Asgharpour M J，Javadian N．Solving a Stochastic Cellular Manufacturing Model by Using Genetic Algorithms［J］．International Journal of Engineering，Transactions A:Basics，2004，17(2):145-155．

［5］ Buzacott JA，Shanthikumar JG．Design of Manufacturing Systems using Queuing Models［J］．Queuing Systems:Theory and Applications，1992，12(1/2):135-213．

［6］ Arghish O，AzadiS，Anvari A，etal．Cellular Manufacturing System design with Queuing Approach［J］．Journal of Basic and Applied Scientific Research，2012，2(11):11884-11890．

［7］ 熊 伟．运筹学［M］．北京:机械工业出版社，2005．

［8］ Salvendy G(著)．郑 立，李从东(译)．工业工程手册［M］．北京:清华大学出版社，2005．

［9］ 曾 勇，董丽华，马建峰．排队现象的建模、解析与模拟［M］．西安:西安电子科技大学出版社，2011．