微通道内交变电场电渗流有限元分析*

张 磊

(青海大学机械工程学院，青海西宁 810016)

0 引言

随着微机电系统(MEMS)的迅速发展，诸如微通道散热器、微混合器、微生物芯片等微流体器件应用越来越广［1］。与宏观系统不同，微通道特征尺度小，流体比表面积增加，流动雷诺数低，并且流体流动的伯克利数较大，这些特点都使得微流体的驱动和控制较为困难［2］。深入研究微流体流动特性，对微流体器件的设计具有重要意义。电渗驱动微流体具有结构简单、控制方便等优点，是微流体器件中广泛应用的一种驱动控制方式。国内外学者对稳定电场作用下的电渗流进行了大量研究，取得了众多成果。而交变电场由于随时间周期性变化，使得其电渗流也随之周期性变化而不稳定，正是这种不稳定流动成为了提高流体输运速度和混合效率的有效方法［3］，近年来也受到了众多学者的关注。

1998 年，Ramos等［4－5］首次运用交变电场驱动微通道中的流体，并且通过计算和实验研究了对交变电场电渗流动产生影响的各种作用力，建立了一种描述交变电场电渗流的频率相关性模型。Luo［6］等通过比较研究矩形弯道中交变与稳定两种电场瞬时电渗流，阐述了外加电场与横向流场变化关系。Yang等［7］和 Marcos等［8］通过研究两种不同矩形微通道中交变电场电渗流，发现主流区内流体流速在外加电场的频率足够大时变化缓慢。Oddy［9］等人的研究则证明了利用交变电场驱动电渗流造成流动混乱，可以有效地提高流体的混合效率。Sasaki［10］等人针对某种特定交流电渗微混合器，进行了理论和实验研究，经过对比两者结果，分析了流体混合与电场频率、电压以及电解液粘度的关系。

笔者在之前已深入研究了电场频率对交变电场电渗流的影响［11］，研究发现，交变电场电渗流瞬态速度呈“波浪状”分布，微通道主流区域流体速度落后于双电层流体速度，流体越靠近通道中心，流速的滞后量越大;随着电场频率的增大双电层滑移速度减小。笔者在之前研究基础上，基于有限元法，数值模拟二维微通道内交变电场电渗流，进一步研究溶液浓度、电场强度和微通道高度等对交变电场电渗流的影响，为精确控制交变电场电渗流提供更多理论依据。

1 交变电场电渗流模型

1．1 物理模型

采用2D平行板微通道，其高度为2 H，长度为L，如图1所示。

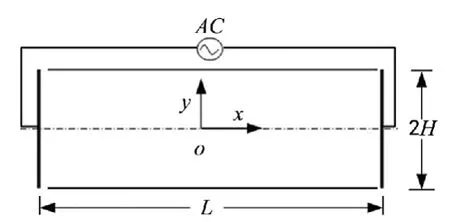
图1 2D平行板微通道示意图

1．2 数学模型

1．2．1 双电层场

由静电学理论可知，单位体积内净电荷密度ρe与双电层电势ψ之间关系可由Poisson方程得:

式中:ε0为真空介电常数;εr为电解质溶液相对介电常数。

假设电解质溶液中单位体积内离子浓度服从Boltzmann分布为:

式中:n0为电解质溶液的离子浓度;e为电子所带电荷量;zi为第i种离子的离子价;T为电解质溶液热力学温度;kb为波尔兹曼常数;ni为单位体积内正、负离子浓度。

单位体积内净电荷密度ρe为:

对于包含两种化学价相等、极性相反离子的电解质溶液，式(3)可变为:

将式(4)与式(1)合并，可得Poisson－Boltzmann方程为:

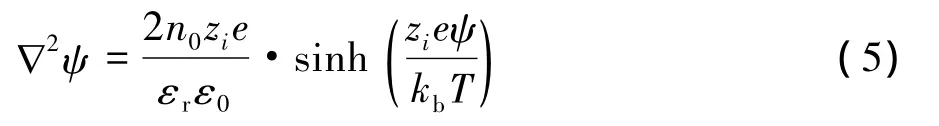
由于双电层厚度远远小于微通道高度，因此可视为微通道壁面处的双电层电位ψ等于zeta电势，由此，边界条件为:

1．2．2 电渗流场

假设微通道中电解质溶液为粘性、不可压缩牛顿流体，考虑双电层场和外加切向电场共同作用下引起的电场力，微通道内流场的描述方程Navier－Stokes方程可修正为:

式中:ρ为微通道中电解质溶液密度;u为流体速度矢量;P为微通道外部压力;μ为电解质溶液的动力粘度系数;FE为外加切向电场作用于双电层所产生的体积力。

式中:ρe为单位体积内净电荷密度，可由式(4)确定;E为外加切向电场的电场强度，文中E为正弦交变电场。

式中:E0为正弦电场的电场强度振幅，ω为角频率。

式中:f为正弦电场频率。

根据微通道壁面处无滑移条件和通道中心对称性要求，边界条件为:

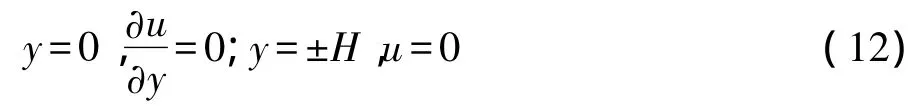
2 数值模拟与分析

对上述2D平行微通道交变电场电渗流数值模拟中，微通道高度为2 H=10～50μm，长度为L=100 μm，微通道两端外加正弦电场 E(t)=E0sin(ωt)，E0=100～500 V/cm，微通道内电解质溶液NaCl的浓度n=10－6～10－2mol/L。其它参数为电子所带电荷量为溶液相对介电常数为εr=80，真空介电常数为ε0=8．854×10－12C2/J·m，e=1．6×10－19C，溶液密度为 ρ=1．0×103kg/m3，溶液动力粘度为 μ=0．9×10－3N·s/m2，波尔兹曼常数为kb=1．38×10－23J/K，热力学温度为T=298 K。

2．1 电场强度的影响

当溶液浓度为10－6mol/L，对应壁面zeta电势为－200 mV，f=10 000 Hz，2H=10 μm，时，电场强度振幅值 E0分别取 100、200、300、400 和 500 V/cm，研究交变电场电渗流与电场强度之间的关系。图2所示为交变电场电渗流在不同电场强度时的瞬态速度分布，图3为双电层滑移速度与电场强度的关系图。

图2中显示，交变电场电渗流的“波浪状”速度流型随电场强度增大波浪的起伏更为显著，同时电渗流速度也随之增大。速度最大值出现在微通道中双电层与主流区域交界处，被定义为双电层滑移速度［12］。图3说明电场频率与双电层滑移速度成正比关系。

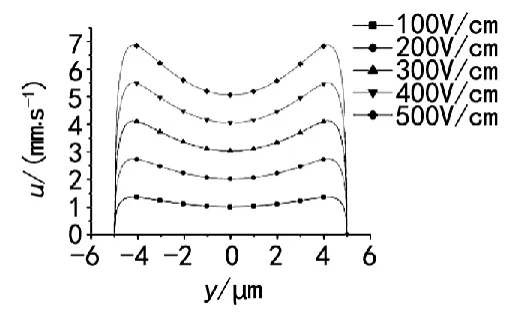
图2 不同电场强度微通道内电渗流速度分布(ωt=π/2)

图3 双电层滑移速度与电场强度的关系

2．2 溶液浓度的影响

由Poisson－Boltzmann方程和修正后的 Navier－Stokes方程可知，zeta电势和溶液浓度等电渗流有着重要的影响。Li等［13］实验研究发现了zeta电势与溶液浓度之间的一一对应关系。即:当溶液浓度分别为10－6、10－5、10－4、10－3和 10－2mol/L 时，对应微通道壁面 zeta 电势为－0．2、－0．15、－0．1、－0．08 和－0．06 V，研究 E0=100 V/cm，f=10 000 Hz，2H=10 μm 时，交变电场电渗流和溶液浓度的关系。

微通道内双电层电势分布与溶液浓度的关系，如图4所示，随着溶液的浓度增大，双电层电势分布由“塞形”逐渐趋向于“矩形”。这是由于双电层厚度受溶液浓度的影响，溶液浓度越大则双电层越薄，因此当溶液浓度增大时双电层电势的变化就会集中在很薄的双电层内部，导致“矩形”电势分布，并且使得电场力作用区域减小。

图5所示为交变电场电渗流在不同溶液浓度时瞬态速度分布。由于电渗流速度受zeta电势的影响，而zeta电势与溶液浓度之间一一对应，且为非线性的对应关系，因此电渗流速度大小受溶液浓度的影响，交变电场电渗流双电层滑移速度随着溶液的增大呈现出非线性下降的趋势，如图6所示。并且，正如前文所述，双电层由于溶液的浓度增大而变薄，所以受到外加交变电场作用的双电层区域减小，使得交变电场电渗流瞬时速度流型具有更为尖锐的波峰。

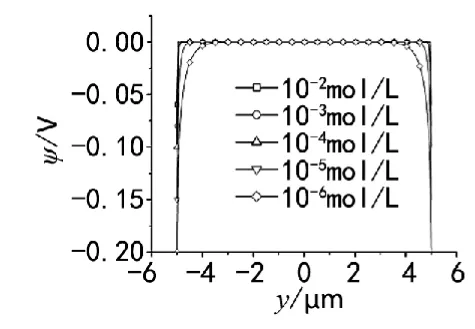
图4 不同溶液浓度微通道内双电层电势分布

图5 不同溶液浓度微通道内电渗流速度分布(ωt=π/2)

2．3 微通道高度的影响

当 E0=100 V/cm，f=10 000 Hz，溶液浓度为10－6mol/L，对应壁面zeta电势为－200 mV时，取微通道高度2 H分别为10、20、30、40和50μm时，研究交变电场电渗流与微通道高度的关系。从图7中容易发现，微通道高度增大时，虽然电解质溶液的浓度不发生改变，双电层的厚度就不会发生变化，但是双电层相对厚度(双电层厚度与微通道高度比值)却在减小，因此，与溶液浓度对双电层电势分布的影响相似，双电层电势分布同样会随着微通道高度的增加逐渐由“塞形”向“矩形”过渡。

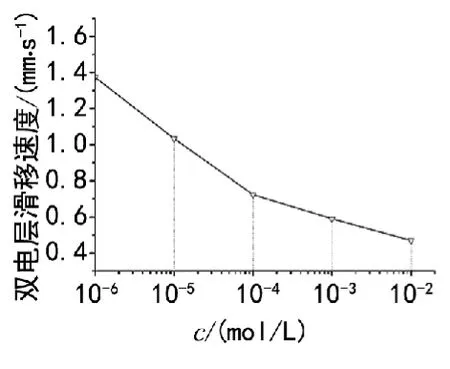
图6 双电层滑移速度和溶液浓度的关系

图7 不同微通道高度微通道内双电层电势分布

交变电场电渗流在不同微通道高度时的瞬态速度分布如图8所示，由于微通道高度的不断增加，造成微通道中心距离壁面或双电层区域越来越远，中心区流体速度落后于壁面的现象更为严重，甚至出现微通道中心区域部分流体仍然保持静止的情况。这主要是因为，微通道中受切向电场作用而产生运动的流体集中在双电层内部(壁面附近)，这部分流体运动后通过流体间粘性力的作用“拖动”中心区域的流体产生运动。而当微通道高度增大后，这种运动的传递需要更多的时间才能够到达通道中心区域，因此，对于高度较大的微通道，只有通过减小交变电场频率或增大交变电场强度的方法，才能够完全驱动微通道内所有区域的流体产生运动。

图8 不同微通道高度微通道内电渗流速度分布(ωt=π/2)

3 结论

基于有限元法，应用COMSOL Multiphysics软件对交变电场驱动微通道内电渗流进行了数值模拟，研究了溶液浓度、电场强度和微通道高度等对交变电场电渗流的影响，得出如下结论:

(1)微通道内交变电场电渗流速度随着电场强度的增大而增大，并且电场强度与双电层滑移速度成正比。

(2)微通道内电渗流速度和双电层滑移速度均随溶液浓度的增大而非线性减小，并且双电层相对厚度会随着溶液浓度和微通道高度增大而减小，使得交变电场电渗流瞬态速度流型中的波峰更加尖锐。

结论表明，准确把握以上因素可实现对交变电场电渗流的精确控制，并为微流控技术提供理论参考。

［1］ 谭德坤．微流道内表面效应对流体流动及传热特性的影响［D］．南昌:南昌大学，2014．

［2］ 李宇杰，霍 曜，李 迪，等．微流控技术及其应用与发展［J］．河北科技大学学报，2014，35(1):11－19．

［3］ 张 凯．微器件中流体的流动与混合研究［D］．杭州:浙江大学，2007．

［4］ Ramos A，Morgan H，Green NG，etal．ACElectrokinetics:a Review of Forces in Microelectrode Structures［J］．Journal of Physics D，1998，31(18):2338－2353．

［5］ Ramos A，Morgan H，Green N G，et al．AC Electric－Field－Induced Fluid Flow in Microelectrodes［J］．Journal of Colloid and Interface Science，1999，217(2):420－422．

［6］ WinJet Luo，YuJen Pan，RueyJen Yang．Transient Analysis of E-lectro－osmotic Secondary Flow Induced by Electric Field in a curved rectangularmicrochannel［J］．J．Micromech．Microeng，2005，15(3):463－473．

［7］ Yang J，Bhattacharyya A ，Masliyah JH，etal．Oscillating laminar electrokinetic flow in infinitely extended rectangular microchannels［J］．Journal of Colloid and Interface Science，2003，261(1):21－31．

［8］ Marcos，Yang C，Ooi T K，et al．Frequency－dependent laminar Electroosmotic Flow in a Closed－end RectangularMicrochannel［J］．Journal of Colloid and Interface Science，2004，275(2):679－698．

［9］ Oddy M H，Santiago JG，Mikkelsen JC．Electrokinetic instability micromixing［J］．Analytical Chemistry，2001，73(24):5822 －5832．

［10］ Sasaki N，Kitamori T，Kim HB．Experimental and Theoretical Characterization ofan ACElectroosmotic Micromixer［J］．Analytical Sicences，2010，26(7):815－819．

［11］ 张 磊，刘 莹．微通道内电场频率对电渗流影响的数值模拟［J］．机械设计与研究，2011，27(3):35－38．

［12］ 吴健康，王贤明．生物芯片微通道周期性电渗流特性［J］．力学学报，2006，38(3):309－315．

［13］ Arulanandam S，Li D．Liquid transport in Rectangular Microchannels by Electroosmotic Pumping［J］．Colloids and Surfaces A:Physicochemical and Engineering Aspects，2000，161(1):89－102．