黏土颗粒扩散双电层影响因素分析
2022-06-14杨成松张莲海周成林韩大伟石亚军
尚 飞, 杨成松, 张莲海, 周成林, 韩大伟, 石亚军
(1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,甘肃兰州730000; 2.中国科学院大学,北京100049; 3.磁共振冻土成冰过程动态分析联合实验室,甘肃兰州730000)
0 引言
土体颗粒的双电层结构与土的物理力学性质关系密切[1-2]。土体颗粒中的黏土矿物因同晶型替换、离解以及吸附等作用而使颗粒表面带有负电荷,在电场作用下,土体中的阳离子(如钠离子、钾离子等)和极性水分子会受到静电吸引作用而吸附在颗粒表面附近,在静电作用和分子热运动的共同作用下,颗粒表面的负电荷和受到静电吸引作用的阳离子以及极性水分子共同形成了黏土颗粒的扩散双电层结构[1-3]。扩散双电层之外的孔隙水被视为自由水,而双电层之内的结合水,依据所受电场力的强弱,将结合水划分为强结合水和弱结合水,这也将会导致二者的相对介电常数存在差异,使得颗粒表面附近的水表现出较为复杂的物理性质,对土的物理力学性质、热力学性质造成影响。
扩散双电层理论最早由Helmholtz 于1890 年提出,Helmholtz认为带电体的表面电荷与反离子构成平行的两层,将之称为双电子层,双电层之间的距离约等于离子半径,类似于一个平行板电容器,在双电层内部电势随距表面距离的增加呈直线下降[4-7]。该模型的缺陷[7]在于忽略了离子的热运动,在低电解质浓度条件下并不适用。随后,Gouy 与Chapman 等进一步修正Helmholtz 模型并提出了考虑静电吸引作用和分子热运动的Gouy-Chapman(GC)模型[4,8],同时阴阳离子分布满足Boltzmann 分布[9-10],但GC 模型关于将离子视为点电荷的假设并不符合物理实际,因此该模型只适用于溶液浓度较低和表面电势较低的计算中。针对上述理论模型的缺陷,Stern等[5-6,10]对GC模型作了进一步改进,考虑了吸附在颗粒表面上离子的尺寸大小,吸附离子的电性中心构成了Stern 面,Stern 面与颗粒表面之间的区域则为Stern 层(双电层内层)。在Stern 层内部,电势的变化规律与Helmholtz 模型一致[6,10];而在Stern 层之外,离子在扩散层中呈扩散分布,电势的变化规律按照GC 模型计算,从而避免了GC 理论只适用于低浓度计算的缺陷。后续逐渐发展的模型包括Grahame理论模型[11]和BDM模型[10],二者分别考虑了离子水合和离子溶剂化对双电层的影响,将双电层的内层细化分为内Helmholtz 层和外Helmholtz 层,但Grahame 模型主要用于解释汞-水界面的双电层电势分布[3],BDM 模型存在电荷不连续效应。
土体中粒径小于5 μm的微粒被称为黏粒,黏粒具有明显的胶体化学特性。土体黏粒的双电层结构与土的物理力学性质的关联主要体现在三个方面:(1)利用双电层理论研究黏土的可压缩性[12-16];(2)基于双电层排斥力推导土壤吸附势[17-20];(3)利用GCS 双电层理论分析冻土中的未冻水含量和水分迁移[21-24]。以上研究均基于扩散双电层理论进行,因而一个合理且能反应各影响因素作用的扩散双电层理论模型显得尤为重要。除此之外,随着双电层研究的不断深入,黏土颗粒的双电层结构与土的物理力学性质的联系将更加清晰地展现出来[1]。
针对于颗粒扩散双电层的影响因素分析,众多学者开展了双电层理论验证与数值模拟计算工作。Bolt[25]推导了介电饱和、离子间相互作用以及离子极化对双电层结构影响的表达式,发现GC 理论的计算结果与试验结果吻合较好。Iglič 等[26]通过改进后的Gongadze-Iglič 模型考虑了阴阳离子尺寸不对称性和Stern 层厚度以及水分子的定向排列对双电层结构的影响,证明了高场强作用下水偶极子的定向顺序会导致电解质溶液的相对介电常数降低,而Stern层厚度将会对颗粒表面电容产生明显影响。Alizadeh 等[27]通过在扩散层和Stern 层之间引入缓冲层和表面络合模型研究了温度对双电层结构的影响。Chang 等[28]通过求解考虑离子半径、电解质浓度等参数的Poisson-Boltzmann 方程得到电解质种类以及表面电荷密度对扩散层的影响。Nishiyama等[29]结合三电层模型以及双电层重合的影响,通过对Poisson-Boltzmann 方程进行数值求解研究了离子强度、pH值以及矿物类型等对多孔介质中水膜厚度的影响。Christian 等[9]通过证明双电层中的弱电解质中离子分布同样满足Boltzmann 平衡方程,将强电解质的双电层理论进一步扩展应用至弱电解质。Conway 等[30]研究了变相对介电常数对扩散层电势和Stern 理论的影响。Shang 等[31]利用Stern模型分析了表面电势、Stern 电势以及颗粒比表面积等因素对于扩散双电层电势分布的影响,证明了Stern-Gouy理论模型在岩土工程和环境工程实践中应用的可行性。
本文基于Gouy-Chapman-Stern(GCS)双电层理论,首先考虑双电层中质量守恒和电荷守恒,建立Nerns-Planck 方程和泊松方程的耦合方程,通过COMSOL Multiphysics软件中内嵌的Nernst-Planck-Poisson 方程对双电层理论模型进行建模,实现电势场和浓度场的耦合求解。然后,基于Shang 等[31]中数据进行模型验证,并结合文献[32]对计算结果进行修正,定量分析不同影响因素对扩散双电层计算结果的影响。
1 双电层模型在COMSOL中的实现
1.1 Gouy-Chapman-Stern理论数值化
扩散双电层GCS理论在GC理论的基础上进一步作如下基本假定[4,8,33]:
(1)与阳离子尺寸相比,固体分散相表面可视为平面,电荷密度均匀分布;
(2)扩散层带电离子近似为点电荷,且服从Boltzmann分布;
(3)溶剂通过相对介电常数影响双电层的电势分布,且在双电层范围内假定为常数;
(4)溶液中电解质由简单对称型盐组成;
(5)黏土颗粒与双电层之间不发生离子交换。
根据GCS 理论,扩散双电层为Nernst-Planck 方程与泊松方程的多物理场耦合[33-34]。其中,Nernst-Planck 方程描述系统中所有离子的质量传递;泊松方程描述电荷密度和电场;且认为带电表面附近的离子分布满足Boltzmann 分布。在COMSOL Multiphysics 数值软件中内置的Nernst-Planck-Poisson 物理场控制方程与扩散双电层的控制方程完全相同,因此可以基于COMSOL 软件对黏土颗粒双电层进行模拟分析。
扩散双电层控制方程由稀物质传递方程和静电平衡方程共同组成,稀物质传递和静电平衡方程分别以离子浓度和电势为自变量,相应的控制方程分别如下:
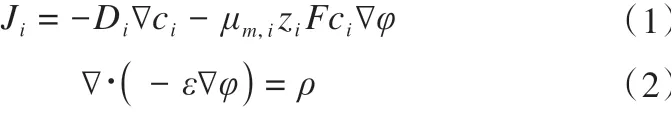
式(1)和式(2)分别为Nernst-Planck 方程和泊松方程。式中:Ji为离子通量,mol·m-2·s-1;Di为扩散系数,m2·s-1;μm,i为迁移率;F为法拉第常数,F=9.6487 × 104C·mol-1;ci为离子浓度,mol·m-3;φ为电解质相中的电位,V;ε为电解质的介电常数,C2·J-1·m-1;ρ为空间电荷密度,C·m-3。
黏土颗粒表面电荷与黏土类型以及颗粒形成环境有关,由于整个体系是电中性的,根据GCS 理论,对空间电荷密度进一步计算得到表面电荷密度。总电荷密度σ与Stern 层电荷密度σ1与扩散层电荷密度σ2之和大小相等,符号相反[31-32],满足:

式中:σ为总电荷密度,C·m-2;σ1为Stern 层电荷密度,C·m-2;σ2为扩散层电荷密度,C·m-2。根据GCS理论[3,31-32],有:
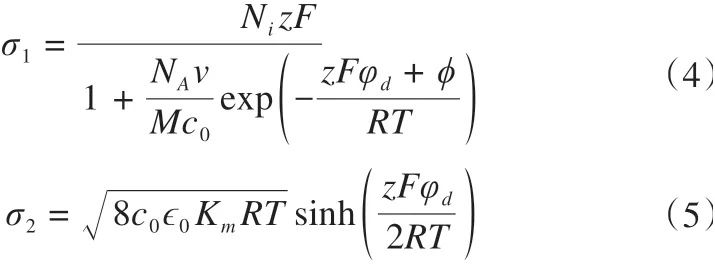
式中:Ni为单位面积上可吸附的离子点位数[3],与阳离子种类有关,1·m-2;z为离子价态;F为Faraday 常数,F= 9.6487 × 104C·mol-1;NA为阿伏伽德罗常数,NA= 6.02 × 1023;v为电解质溶液密度,kg·m-3;M为溶剂的摩尔质量,kg·mol-1;c0为电解质中离子的摩尔浓度,mol·m-3;φd为Stern 电势,V;ϕ为比吸附势,一般可简化为ϕ= 0;R为气体常数,R=8.314 J·mol-1·K-1;T为绝对温度,K;ϵ0为真空介电常数,ϵ0= 8.854 × 10-12C2·J-1·m-1;Km为扩散层电解质的相对介电常数。
表面电荷密度σ可通过阳离子交换量CEC和比表面积S求出,三者之间满足[31-32]:

式中阳离子交换量CEC和比表面积S均可由实验测出。几种常见黏土矿物的阳离子交换量和比表面积值如表1所示。

表1 常见黏土矿物的阳离子交换量和比表面积[31]Table 1 Cation exchange capacity and specific surface area of common clay minerals[31]
联立公式(3)、(4)、(5),即可解得Stern电势φd,当φd已知时,代入σ1与σ2表达式中利用Poisson 方程可进一步求得双电层的电势分布。定义扩散双电层的有效厚度κ-1为[2,24,31]:
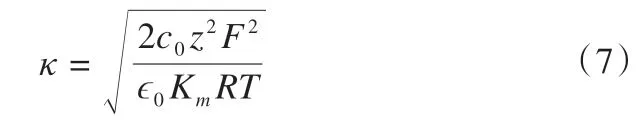
式中:ϵ0为真空相对介电常数,Km为扩散层的平均相对介电常数;T为土体热力学温度,K;c0为本体溶液的摩尔浓度,mol·m-3。为了避免单位混淆,模型中所有参数的单位均采用国际单位制。
1.2 模型验证与分析
为验证COMSOL 软件计算扩散双电层模型的有效性和可靠性,对文献[31]中采用GCS 双电层理论计算温度、浓度对双电层电势分布影响的结果进行对比验证。
1.2.1 模型条件
文献[31]中采用的黏土矿物为伊利石,Stern 层厚度为0.5 nm,溶液温度为273 K 和298 K,求解过程中温度保持不变,溶液初始浓度为1 mol·m-3和10 mol·m-3,电解质为简单对称型盐,离子价态为±1价,矿物颗粒表面为零通量界面,颗粒与双电层之间不发生离子交换,在距离颗粒表面足够远处电解质浓度达到平衡。基于表2 的黏土矿物及溶液,建立扩散双电层几何模型(如图1 所示),将计算得到的电荷密度σ1与σ2分别赋值在颗粒表面和Stern面,利用COMSOL 软件数值模拟温度、浓度对扩散双电层电势分布的影响,进而进行模型验证。
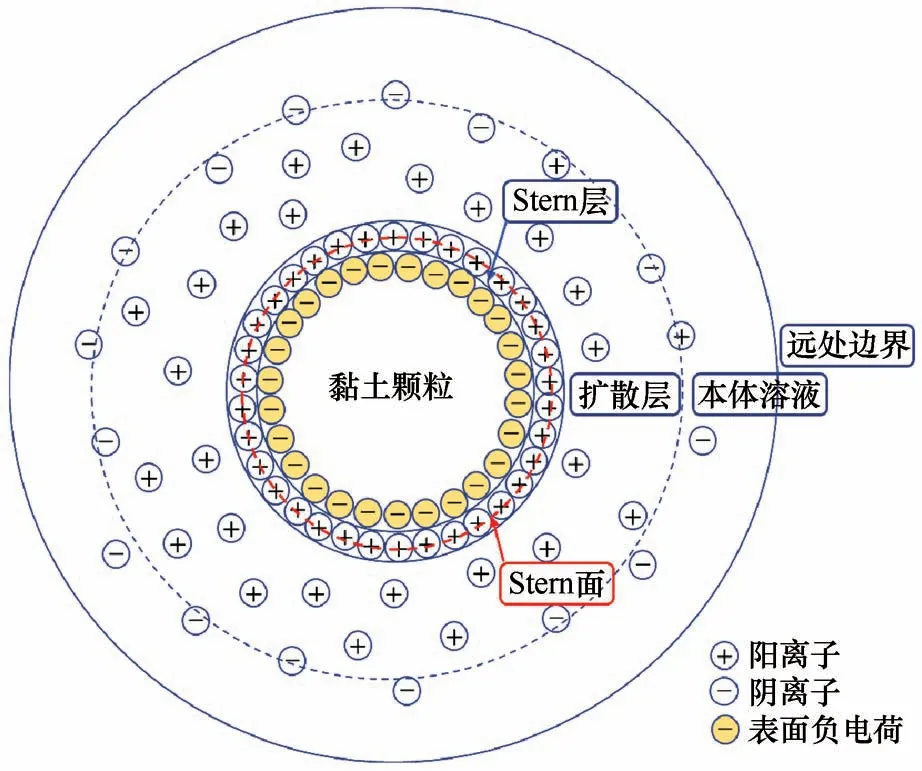
图1 扩散双电层结构几何示意图Fig.1 Geometric schematic diagram of diffused electric double layer structure

表2 扩散双电层模型参数取值Table 2 The parameter values of the diffused electric double layer model
1.2.2 模型验证
图2是不同温度不同浓度情况下模拟计算的电势与颗粒表面距离之间的变化。从图2 可以看出,模型计算结果与文献[31]中电势变化曲线差异较小,仅在Stern 电势数值上存在一定偏差,整体电势变化趋势保持一致。在Stern层内,电势从颗粒表面电势φ0线性下降至Stern 电势φd;在Gouy 扩散层至本体溶液中,电势由Stern 电势呈指数形式下降至0。模拟数值和变化趋势与文献[31]中保持一致,验证了COMSOL 软件计算的有效性和可靠性。因此,可利用该软件进行扩散双电子层影响因素的研究分析。

图2 扩散双电层模型验证:温度为273 K时电势分布(a);浓度为1 mol·m-3和10 mol·m-3时电势分布(b)(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig. 2 Validation of the diffusion electric double layer model:Potential distribution at 273 K(a);Potential distribution at 1 mol·m-3 and 10 mol·m-3 concentrations(b)(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
但由于文献[31]中在表面电荷密度计算过程中M取为电解质的摩尔质量,实际上M应为溶剂的摩尔质量[3,32,35],故在进行模型有效性验证时将M取为电解质的摩尔质量,在后续双电层影响因素分析过程中将M更正为溶剂的摩尔质量。
2 双电层影响因素分析
为研究不同影响因素对扩散双电层电势分布的影响,在上述模型的基础上分别设置不同的条件模拟不同影响因素对颗粒表面电势分布的影响,其中黏土矿物选用伊利石,电解质为氯化钠。当考虑浓度对电势分布的影响时,设置溶液浓度分别为:1 mol·m-3、10 mol·m-3和100 mol·m-3;考虑矿物成分的影响时,黏土矿物分别为伊利石、高岭石以及蒙脱石。
2.1 温度的影响
当溶液温度发生变化时,其相对介电常数也会随之发生改变。因此在考虑温度对扩散双电层电势分布的影响时,必须考虑溶液的相对介电常数随温度的变化。
假定溶液的初始浓度为10 mol·m-3,分别设置温度条件为273 K、293 K以及343 K进行数值分析,相应的扩散层溶液相对介电常数分别为90、80 和63.8,其具体模拟结果如表3 和图3 所示。温度增加时,溶液的相对介电常数减小,在二者的共同作用下颗粒的表面电势和Stern电势略有增加,而扩散层厚度略有降低;表面电势的数值约为Stern电势的5~6倍,这与文献[36]所得试验结果较为接近。

图3 温度对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.3 Effect of temperature on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
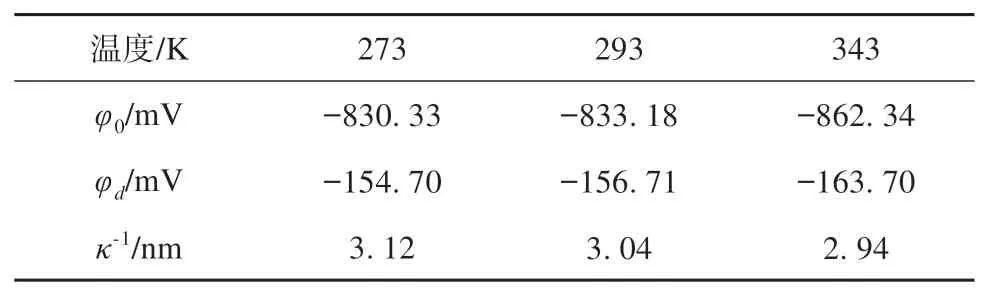
表3 温度对电势分布的影响Table 3 Effect of temperature on potential distribution
而当温度低于273 K 时,土中部分水会冻结成冰,由于冰和水之间的相对介电常数存在明显差异,因而需要考虑冻结相变的影响。根据双电层理论,土中水依据受到的电场作用力强弱可以分为强结合水和弱结合水[1,21,24]。而当土体发生冻结时,一般认为只有弱结合水发生冻结而强结合水不发生冻结,因此当土壤发生冻结时,需将扩散层中已冻结区域与未冻区进行区分。其中未冻水膜的厚度x与温度T之间的关系式[21]为:

式中:κ-1为扩散层的有效厚度为环境温度,K。
因此,若要计算负温条件下温度对扩散双电层电势分布的影响,则需要考虑土中水冻结相变对相对介电常数以及未冻吸附水膜厚度造成的影响。由于负温条件下黏土颗粒表面附近水的赋存状态较为复杂,本文暂不考虑负温对于扩散双电层电势分布的影响,后续将进行进一步的理论分析逐步探讨负温条件下的颗粒扩散双电层的电势分布。
2.2 浓度的影响
当土中水含有电解质浓度不同时,浓度对扩散双电层电势分布有一定影响。因此,设置温度条件为293 K,初 始 溶 液 浓 度 分 别 为1 mol·m-3、10 mol·m-3和100 mol·m-3进行模拟,结果如表4 和图4所示。由表4和图4可知,随着初始溶液浓度的增加,颗粒的表面电势和Stern 电势均减小,Stern 电势变化趋势则更为明显;同时扩散层厚度也随着溶液浓度的增加而明显减小。
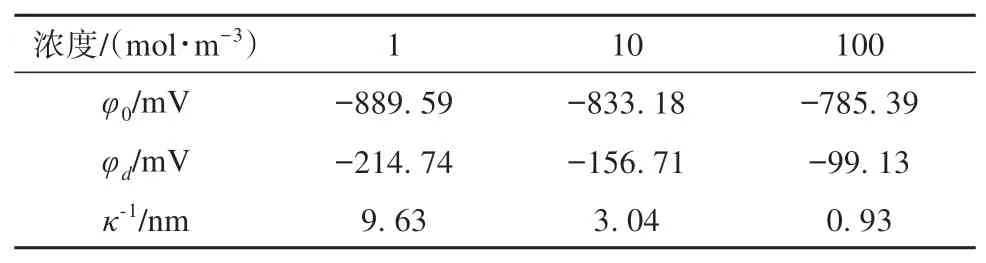
表4 浓度对电势分布的影响Table 4 Effect of concentration on potential distribution
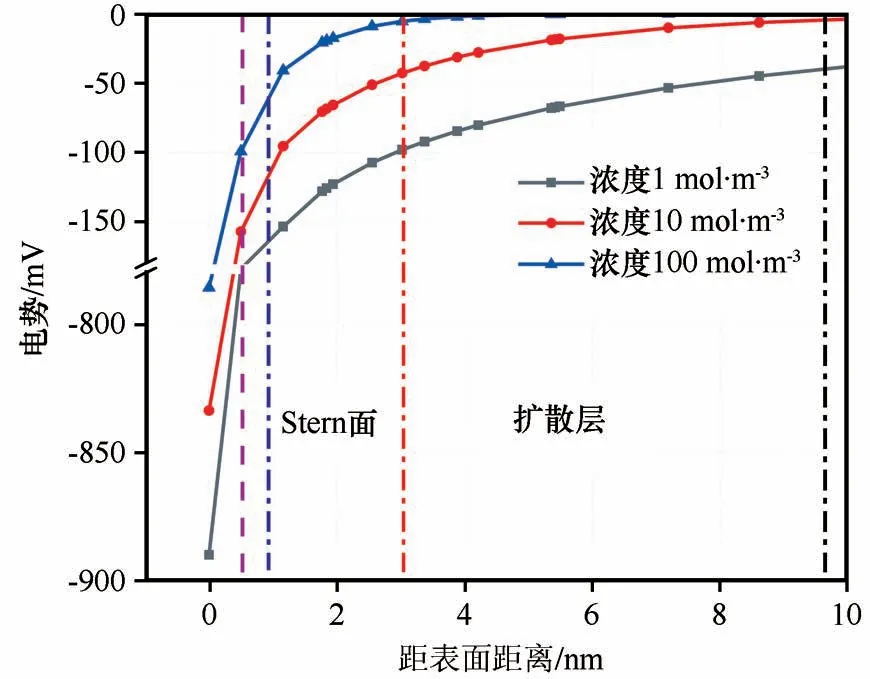
图4 浓度对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.4 Effect of concentration on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
2.3 Stern层厚度的影响
扩散双电层中Stern 层厚度近似等于颗粒表面吸附阳离子的半径,与阳离子种类密切相关[32]。为分析阳离子种类对电势分布的影响,对Stern层厚度分别为0.3 nm、0.5 nm 和0.7 nm 的黏土颗粒进行数值模拟分析,对比分析发现:3 种Stern 层厚度获得的结果的电势变化趋势一致,都随着距颗粒表面距离的增加而减小。由表5 和图5 可知,随着Stern层厚度增加,表面电势φ0明显增加,而Stern 电势φd变化不明显。
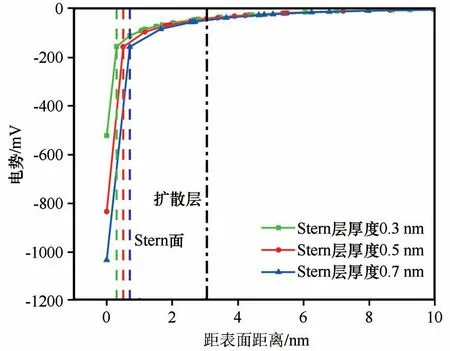
图5 Stern层厚度对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.5 Effect of Stern layer thickness on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
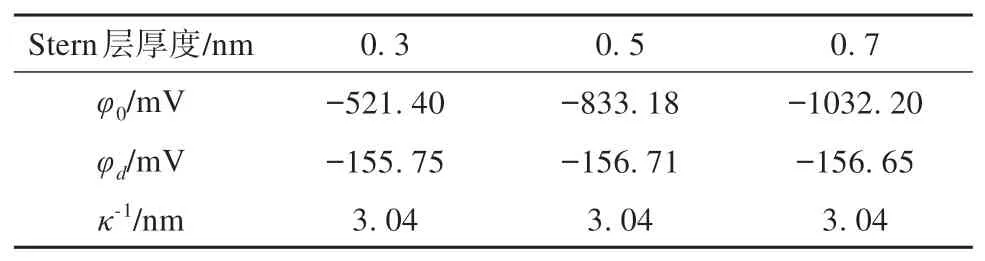
表5 Stern层厚度对电势分布的影响Table 5 Effect of Stern layer thickness on potential distribution
2.4 颗粒尺寸的影响
土实际上是不同粒度成分土颗粒的混合物,其黏土颗粒尺寸大小对电势分布具有一定的影响,分别取颗粒粒径为2 000 nm、1 000 nm、400 nm 以及100 nm 的黏土颗粒进行数值模拟分析。模拟要求除颗粒粒径外,其他条件参数均保持相同,模拟结果如表6 和图6 所示。结果表明,颗粒尺寸对于黏土颗粒表面扩散双电层的电势分布影响较小,随着颗粒粒径增大,Stern 电势几乎不发生任何变化,同时表面电势的变化幅度也较小。这与常规认知存在一定偏差,推断其可能的原因为:在进行电荷密度求解时,已经规定了颗粒的比表面积,而实际上颗粒的比表面积随粒径减小而逐渐增大,与计算采用的恒比表面积存在差异,因而导致模拟结果与常规认知存在差异,后续将依据实验数据对模拟数据再次验证。
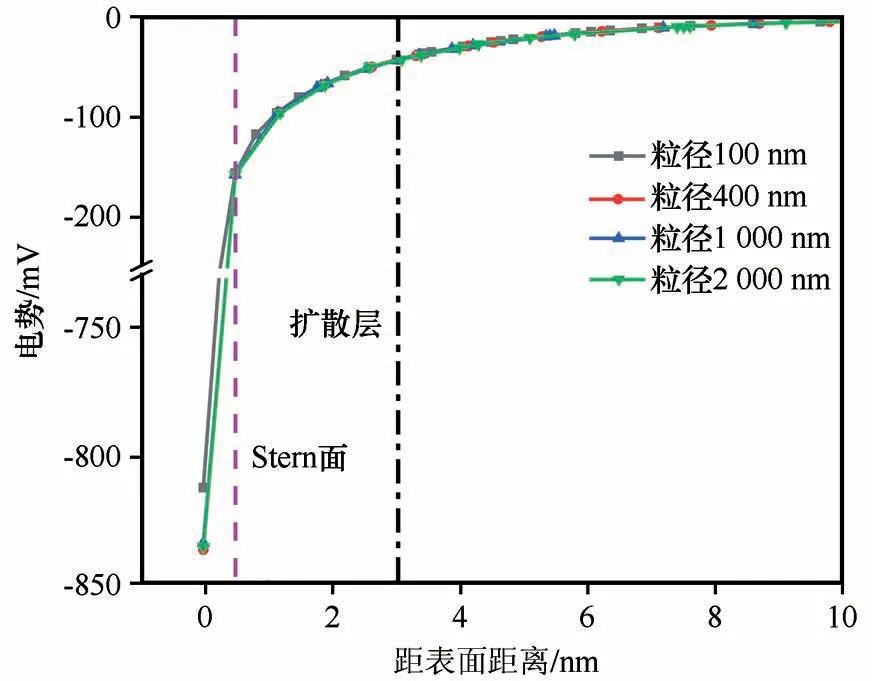
图6 颗粒粒径对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.6 Effect of particle size on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
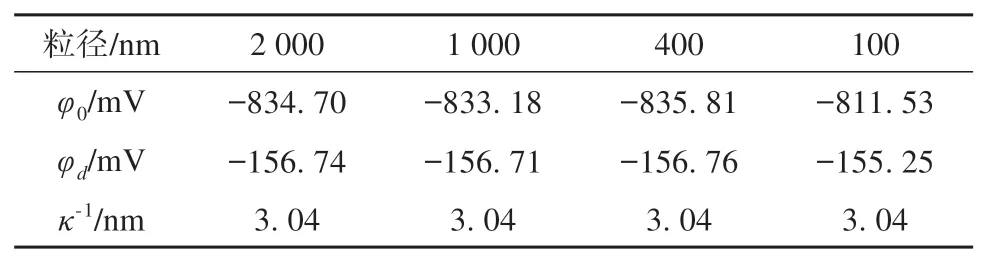
表6 颗粒粒径对电势分布的影响Table 6 Effect of particle size on potential distribution
2.5 矿物成分的影响
土中黏土颗粒的矿物成分往往并不单一,通常是由多种矿物成分共同组成。为研究不同矿物成分对颗粒表面扩散双电层电势分布的影响,分别选取不同的黏土矿物成分进行模拟分析。由表7和图7可知,黏土矿物成分对颗粒表面电势有较为明显的影响,高岭石的表面电势约为蒙脱石表面电势的4倍;而矿物成分对Stern电势的影响小于表面电势;且矿物成分的改变不会造成扩散层厚度发生变化。
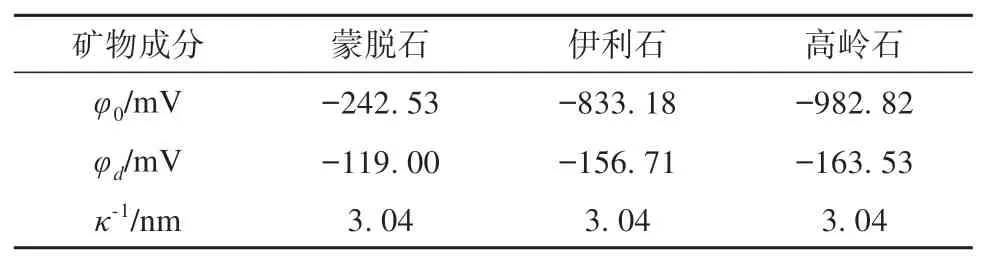
表7 矿物成分对电势分布的影响Table 7 Effect of mineral composition on potential distribution

图7 矿物成分对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.7 Effect of mineral composition on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
2.6 颗粒形状的影响
已知颗粒尺寸对电势分布影响较小,但不同矿物组分具有不同的颗粒形状,比如:一般黏土成分多是次生矿物,形状多为针片状。考虑黏土颗粒间相互接触以及颗粒的不规则形状对双电层电势分布的影响,分别选取圆形、条形和折线形模拟不同颗粒形状对双电层电势分布的影响,其中折线形是为研究颗粒不规则表面处的夹角对电势分布的影响。圆形颗粒(截面)尺寸为半径500 nm,条形颗粒(截面)尺寸为50 nm×500 nm,折线形夹角为120°,其中条形可视为折线形夹角为180°时的特殊情形。分别取圆形任意位置、条形长边中点处、折线角平分线处的电势-距离变化结果,如表8 和图9 所示。
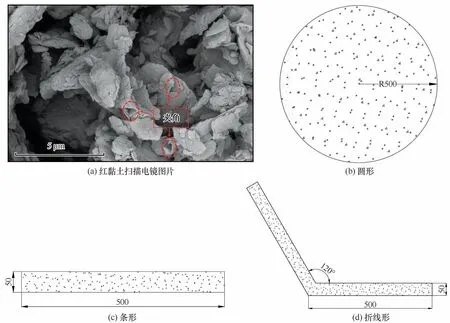
图8 模拟用颗粒形状示意图Fig.8 Schematic diagram of particle shape for simulation:red clay SEM image(a);circle(b);bar(c);broken line(d)
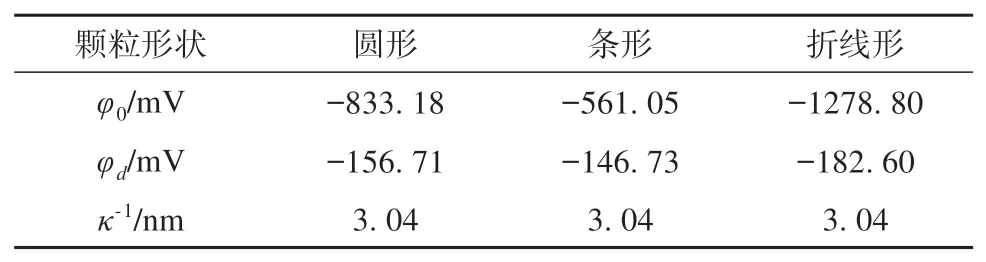
表8 黏土颗粒形状对电势分布的影响Table 8 Effect of clay particle shape on potential distribution
由表8 和图9 可知,黏土颗粒形状对于颗粒表面电势分布影响较为明显。随后,取折线形夹角分别为45°、60°、90°以及150°再次进行模拟分析,结果如表9所示。
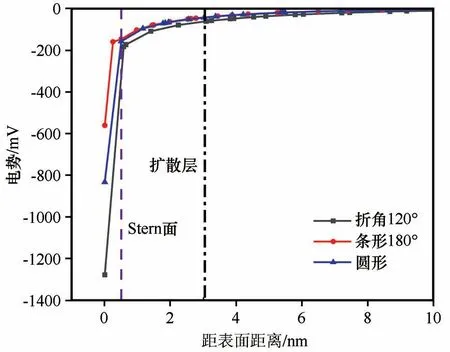
图9 颗粒形状对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.9 Effect of particle shape on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
由表9 和图10 可知,当夹角在45°~90°范围内时,随着角度逐渐增加,表面电势逐渐减小,趋势较为明显;而在90°~180°范围内,随着夹角逐渐增加,表面电势值仍保持减小的趋势,但趋势较为缓慢。而Stern 电势与夹角变化无明显规律。随后分别选取夹角平分线上距颗粒表面0.5 nm 和2 nm 处电势值绘图如图11 所示。由图10 和图11,可以发现,随着夹角逐渐增加,相同位置的电势值逐渐减小,且随着距夹角距离的增加,这种变化影响逐渐减小。

表9 折线夹角对电势分布的影响Table 9 Effect of the angle of the broken line on the potential distribution
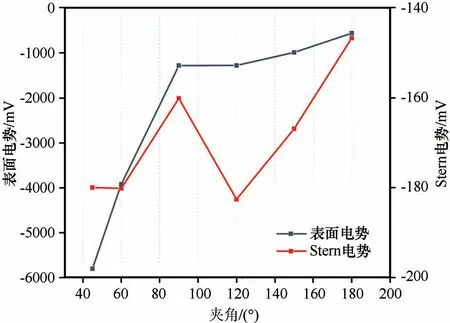
图10 折线夹角对电势分布的影响Fig.10 Effect of the angle of the broken line on the potential distribution
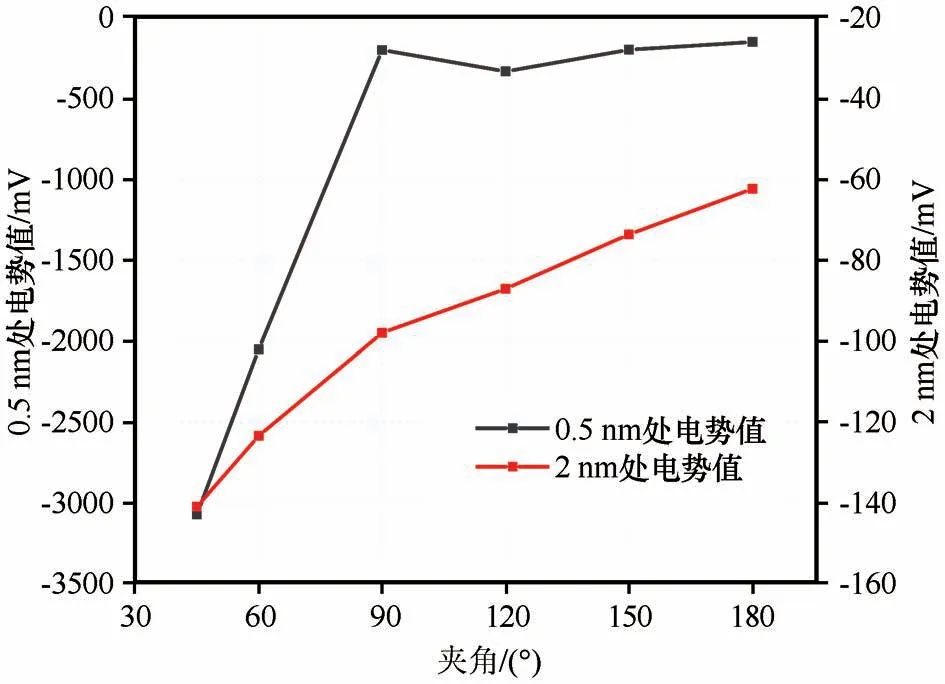
图11 折线夹角对不同位置处电势分布的影响Fig.11 Effect of the angle of the broken line on the potential distribution at different positions
2.7 相对介电常数的影响
在特殊土(如生活垃圾填土)研究中,液体中可能含有低介电常数的液体,比如一些非极性流体。但对于天然黏土来说,可以认为包裹在黏土颗粒周围Stern 层和扩散层的液体介质均为水。对于水来说,由于受到颗粒表面静电作用,Stern 层的相对介电常数远小于扩散层和溶液中的相对介电常数[30-31],因此一般假设Stern 层中液体的相对介电常数为Kd=6,而扩散层和溶液中为Km=80。而对于极性有机流体,一般可假设Kd=3,Km=20。
表10和图12 是溶液相对介电常数对电势分布造成的影响。从图12中可以看出,溶液的相对介电常数对于颗粒的表面电势影响明显,相对介电常数减小时,颗粒的表面电势和Stern 电势均明显增加;但相对介电常数变化对于扩散层厚度的影响较小。

表10 相对介电常数对电势分布的影响Table 10 Effect of relative permittivity on potential distribution
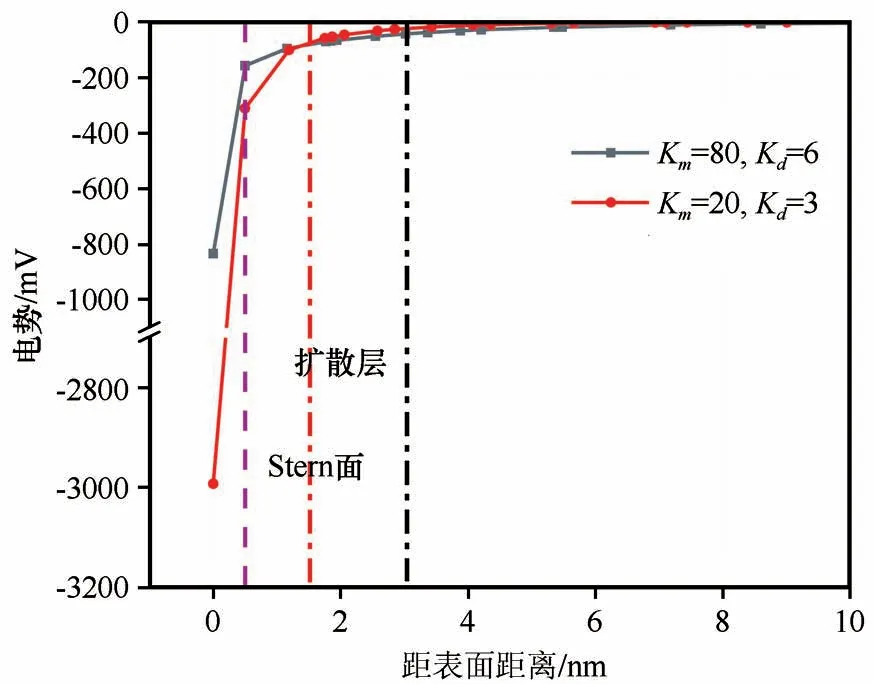
图12 相对介电常数对电势分布的影响(虚线表示Stern面,点划线表示扩散层与溶液的分界面)Fig.12 Effect of relative permittivity on potential distribution(The dotted line represents the Stern surface,and the dashed line represents the interface between the diffusion layer and the solution)
3 结论
基于GCS 扩散双电层理论及其基本假定,将扩散层中的带电离子视为服从Boltzmann 分布的点电荷,建立Nernst-Planck 方程和泊松方程的耦合方程,通过COMSOL Multiphysics 软件模拟了黏土颗粒扩散双电层在不同影响因素下的电势分布,同时结合已有研究结果,验证了COMSOL Multiphysics在求解扩散双电层过程中的有效性,获得的主要结论如下:
(1)在273~343 K 范围内,温度对于黏土颗粒表面电势分布的影响小于Stern 电势;随着温度增加,表面电势和Stern 电势均略有增加,但变化幅度不明显。
(2)在一定的浓度范围(1~100 mol·m-3)内,随着溶液浓度逐渐增加,颗粒表面电势和Stern电势均减小。
(3)吸附阳离子不同,造成Stern层厚度不同,不同的Stern 层厚度对于扩散双电层电势分布影响明显。随着Stern 层厚度的增加,表面电势明显增加,但Stern电势几乎不发生变化。
(4)当规定了颗粒矿物成分时,颗粒尺寸对于扩散双电层电势分布的影响很小,当尺寸在100~2 000 nm 范围内,尺寸变化对电势分布的影响可以忽略不计;但颗粒形状对电势分布的影响极为明显,当颗粒存在夹角时,夹角处的电势远大于其他位置,且夹角越小,颗粒的表面电势越高。
(5)黏土矿物成分对于颗粒电势分布的影响较为明显,其原因是矿物成分通过阳离子交换量和比表面积控制电荷密度,进而影响颗粒表面附近的电势分布。
(6)溶液的相对介电常数对电势分布影响明显。当相对介电常数减小时,颗粒的表面电势和Stern电势增加,且表面电势的变化量远大于Stern电势。
