长寿互换的运行机制与定价模型

谢世清

(北京大学经济学院，北京 100871)

引言

近半个世纪以来，科技进步和经济发展使得人们的生活水平日益提高，世界人口的年龄分布正发生着深刻变化，死亡率持续下降，逐步走向人口老龄化，并导致了系统性的长寿风险。对个体而言，可通过社会养老保险或年金来减轻生存期延长带来的财务压力。但对提供此类服务的年金保险公司而言，在投保群体中系统性存在的长寿风险难以通过大数法则进行分散。为吸收长寿风险的最终损失，年金保险公司需保证一定数量的经济资本，但经济资本占用将损害保险公司的盈利能力。因此，系统性长寿风险仍是年金保险公司亟待解决的问题。

近年来，长寿风险证券化已成为长寿风险管理领域中的重要创新，是寿险证券化中颇为活跃的领域。尤其是2008年国际金融危机后，在国际市场上不断涌现出一些新产品，如长寿债券、长寿互换和q远期合约等衍生品。其中，长寿互换是指一种交易双方基于目标人群未来实际生存率和预期生存率之间的差异定期交换现金流的合约，是一种重要的长寿风险证券化产品。与长寿债券相比，长寿互换有着交易成本低、操作简捷、灵活性高等优势，因此在金融市场具有较强的吸引力。

目前国外对长寿互换的研究主要集中在两个方面：首先，在运行机制上，Lin and Cox (2005)[8]对触发型长寿债券现金流进行了调整，率先设计出带触发机制的长寿互换。在其基础上，Dowd et al.(2006)[7]进行了设计上的改进，提出了普通长寿互换；其次，在定价方法上，Dowd et al.(2006)[7]、Dawson et al.(2010)[5]和Chang et al.(2010)[4]提出了对长寿风险进行Wang转换的定价解析式。国内关于长寿互换的研究甚少，本文旨在对长寿互换的运行机制和定价模型进行分析，以填补这一领域的缺失。

长寿互换的市场发展

一、长寿互换的市场发展情况

2008年7月，J.P.摩根向加拿大寿险公司发行了第一笔长寿互换合约。该长寿互换合约的面值为5亿英镑，有效期40年。该长寿互换与q远期合约相比有三点显著区别：(1)不与市场公开发布的死亡率指数挂钩，转移的是加拿大寿险公司英国年金业务中12万5千人以上年金受益人实际的长寿风险；(2)不是风险价值的对冲工具，而是每年的现金流对冲工具；(3)长寿风险通过J.P.摩根直接转移到资本市场投资者(Blake et al., 2013)[2]。

与长寿债券市场相比，长寿互换的市场发展非常迅速。继2008年加拿大寿险公司和J.P.摩根签订了第一笔长寿互换合约以后，全球又进行了多笔长寿互换交易。其中，仅在英国市场上就有6笔发行到资本市场。如表1所示，2008～2012年，英国市场上长寿互换发行面值总额达到76亿英镑。其中，最大规模面值的长寿互换发行金额高达30亿英镑，是劳斯莱斯公司2011年11月针对英国分公司养老计划的长寿互换。

值得注意的是，长寿互换还有另一种再保险性质的长寿互换。第一笔再保险性质长寿互换于2007年4月发行，交易双方为瑞士再保险和英国寿险公司Friends Provident，其长寿风险来自于Friends Provident在2001～2006年间签订的包含7万余人、总额为17亿英镑的养老金合约。再保险性质的长寿互换并非真正的资本市场工具，其风险转移也仅限于再保险公司。限于篇幅，本文只讨论将长寿风险转移到资本市场的非再保险性质的长寿互换。

与长寿债券相比，长寿互换具备一些显著优势：(1)长寿互换的发行成本较低，且相对更易取消；(2)作为柜台交易的产品，长寿互换能按照投资者特殊的长寿风险管理需求为其“量身定做”，比债券更能适宜多变的市场环境；(3)长寿互换的发行并不依赖于有较强流动性的市场，其发展的动力来源于承受死亡率风险的交易双方的相对优势，或交易双方对未来死亡率不同的看法(Dowdet al., 2006)[7]。

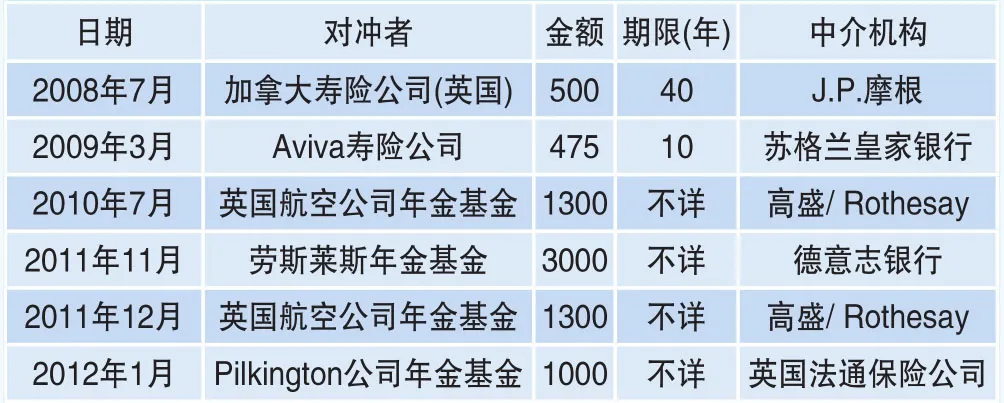
表1 2008～2012年发行到资本市场的长寿互换 (单位：百万英镑)

二、市场发展的推动与障碍因素

长寿互换市场发展的推动因素主要有以下三个方面：首先，长寿互换能够为年金保险公司提供多种风险管理手段：(1)不同国家或地域人群的死亡率之间的相关性较低，跨境的长寿互换能够实现对不同人群的长寿风险进行多元化经营管理；(2)不同年龄段人群对年金产品的需求不同，通过长寿互换可使年金保险公司获得不同年龄段的长寿风险暴露，对其死亡率期限结构进行调整；(3)长寿互换还包括死亡率差额互换、跨币种长寿互换、以非死亡率指数为标的的长寿互换以及内含期权的长寿互换等(Dowd et al., 2006)[7]。

第二，长寿互换也受到投资银行等金融机构的青睐。首先，长寿互换是基于年金保险公司承受的长寿风险发展而来的金融衍生品，而目标群体的死亡率与宏观经济运行并无显著联系(Beta较低)，所以金融机构会利用长寿互换来分散风险。与此同时，投资银行通过与保险公司进行长寿互换并同时发行死亡率债券，可获得较高的中间利润。所以，长寿互换受到市场金融机构的广泛关注。

第三，长寿互换等非标准化合约与债券等传统场内工具能相互匹配并充分管理长寿风险。首先，场内市场交易具有流动性、交易机制设计等方面的优势。场内市场可设计标准化合约、设置死亡率指数，以增加合约最终使用者数量和类型，从而将各种信息和预期迅速反映到市场竞争中，提高市场透明度和风险配置效率。而场外市场可为投资者量身设计用以对冲系统性死亡率风险的非标准化合约，从而有效降低“基差风险”。

另一方面，长寿互换市场发展还存在三点障碍因素：(1)长寿互换交易属于场外市场交易，其交易成本相比标准化的场内交易合约而言更高；(2)长寿互换也容易产生一定的违约的信用风险；(3)由于长寿风险目前还难以用模型精确地刻画，很难保证对长寿互换进行精准的建模定价，难以使互换双方的损失与收益互惠对等。

长寿互换的运行机制

长寿互换(longevity swaps)是针对目标人群潜在长寿风险的双方协议。互换双方约定在协议到期前，基于目标人群未来实际生存率和预期生存率之间的差异而定期交换现金流。Dowd et al.(2006)[7]首先提出了普通生存互换(vanilla survivor swaps)概念，通常简称为长寿互换(longevity swaps)，即互换一方以固定现金流交换另一方根据实际生存率水平决定的浮动现金流。此外，Sweeting(2007)[9]、Biffis and Blake(2009)[1]和Chang et al.(2010)[4]等也对长寿互换进行过研究。

Lin and Cox(2005)[8]对触发型长寿债券现金流进行了调整，率先设计出带触发机制的长寿互换。他们首先将长寿债券中年金保险公司期初支付的费用平摊为有效期内的一系列固定现金流，投资银行每年依据实际生存率和触发阈值来确定支付给年金保险公司的实际浮动现金流。这样便构成了由固定支付与浮动支付组成的长寿互换。

在Lin and Cox(2005)[8]的研究基础上，Dowd et al.(2006)[7]提出了长寿互换，其运行机制如图1所示：每年，年金保险公司(长寿风险对冲机构)从投资银行(长寿互换提供商)处获得浮动现金流Bt，即根据年金保险公司保单池真实死亡率或市场公开死亡率指数计算出来的支付额。相应地，年金保险公司每年向投资银行支付固定额(1+π)Ht，其中，Ht为根据生命表中目标人群的预期生存率，π为互换价格。

假设年金保险公司保单池内被保人年龄为X，人数为lx，则t年后保单池内被保人数为lx+t，每人每年收到的年金金额为h。因此，年金保险公司在保险市场上每年给付给保单受益人的年金总额为lx+t×h。假设互换合约不存在基差风险，则有Bt=lx+t×h。

一般而言，互换双方每年只交换净现金流，即如果(1+π)Ht大于Bt，则年金保险公司将向投资银行支付净现金流((1+π)Ht-Bt)；若(1+π)Ht小于Bt，则投资银行将向年金保险公司支付净现金流(Bt-(1+π)Ht)；当(1+π)Ht等于Bt时，该互换在t时刻净现金流为零。综合考虑年金保险公司在保险市场和长寿互换中的各现金流，可得每年总净现金流出为：lx+t×h+(1+π)Ht-Bt=(1+π)Ht。

图1 长寿互换的运行机制

上式中，(1+π)Ht在期初互换协议签订时便已确定。由此可见年金保险公司通过长寿互换可使每年的总净现金流出确定，避免了随机风险，从而能够对长寿风险进行对冲。若在一定时期内目标人群的寿命大于预期水平，年金保险公司虽然因原始保险市场上的年金支付金额增加遭受损失，但可被与此同时在长寿互换上的收益所对冲。因此，该长寿互换可以使年金保险公司对其所面临的长寿风险实现长期而又“量身定做”的对冲。

然而，长寿互换中年金保险公司承担着基差风险。如果浮动现金流与市场指数挂钩，而不是由保单池真实生存率决定，即Bt往往不等于lx+t×h。若保单池真实生存率高于市场同期水平，年金保险公司则不能对冲所有长寿风险。因此，如何对基差风险进行有效的测量和控制对长寿互换市场的发展十分重要。Sweeting(2007)[9]在给互换定价时考虑了基差风险，并认为当标的保单的被保人寿命不小于市场指数相关人群的寿命时，基差风险将很小。

值得注意的是，长寿互换与金融市场上的利率互换类似，两者都是固定现金流和浮动现金流进行交换，但两者存在着以下三点差异：(1)利率互换的固定现金流数额在到期日前通常保持不变，但长寿互换的固定现金流数额通常随着时间推移由于预期年金支付额的减少而下降(见图2)；(2)与利率互换浮动现金流挂钩的市场指数一般是市场利率指数(如LIBOR)，而与长寿互换浮动现金流挂钩的市场指数一般是死亡率指数；(3)由于货币市场流动性高、利率期限结构完整，所以可用无套利方法对利率互换进行定价，而长寿互换市场是不完整的，基本不用该法对其进行定价(Dowd et al., 2006)[7]。

图2 长寿互换现金流示意图 (单位：百万美元)

长寿互换的定价模型

金融市场中的利率互换可以采用资本资产定价模型(CAPM)和无套利方法进行定价。但由于长寿互换市场的不完全性，这两种定价方法并不适用于长寿互换。目前，国外学者主要采用Wang转换定价法(Lin and Cox,2005; Dowd et al., 2006; Chang et al., 2010)[8][7][4]和风险中性定价法(Cairns et al., 2006; Dawson et al., 2010; Deng et al., 2012)[3][5][6]对长寿互换和长寿q远期合约进行定价。本文采用单因子Wang转换定价法推导长寿互换的具体定价解析式。

一、Wang转换方法

首先，阐述单因子Wang转换定价方法。Wang(2000)[10]假设FX(x)=Pr(X≤x)是随机变量的累积概率分布函数，0≤FX(x)≤1，λ为风险的市场价值，Φ(x)为标准正态分布的累积概率分布函数，则单因子Wang转换算子为：

其中，λ能够根据市场上可交易的金融资产的价格进行计算。假设寿险年金市场中第t年的生存率的随机分布为pt，记F(pt)为其累积概率分布函数，则通过Wang转换后的生存率累积概率分布函数为：

二、服从OU过程的生存指数模型

其次，采用带Ornstein-Uhlenbeck(OU)跳过程的死亡率序列来刻画生存指数(尚勤，2008)[11]。假设随机计数过程N是双随机的，强度为λ(与前文中的风险市场价值不同)，则Ns-Nt服从参数为的泊松分布。假设期初寿命为x的人群的未来寿命Tx服从强度为λx的双随机停时，即强度为λx的随机计数过程N的首次跳跃时刻为Tx，且当时Tx＞t,Nt=0，当Tx≤t,时，Nt＞0，则生存函数可写为：

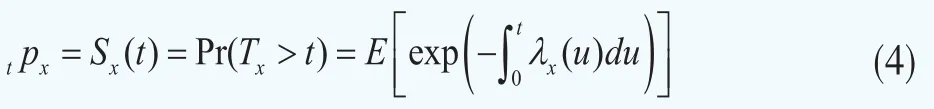
再设λx服从带跳的OU过程，即：

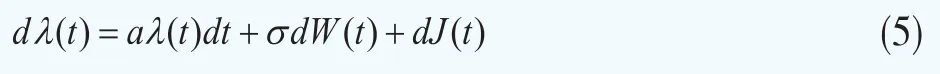
其中，W(t)是标准布朗运动；J(t)是纯复合泊松跳跃过程，泊松到达强度为l＞0，跳跃幅度服从均值为μ＜0的指数分布，且布朗运动、泊松过程以及指数分布彼此相互独立。

在λx服从具有上述特征的分布的基础上，根据式(4)，生存概率t Px可以表述为：

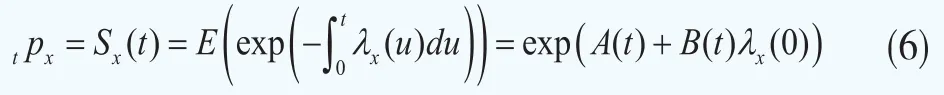
其中，A(t)和B(t)需要通过解下列常微分方程组得出：

当边界条件为A(0)=0，B(0)=0时，求解可得：

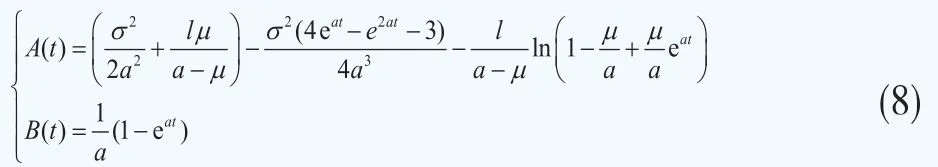
这样，生存概率t px可以进一步表述为：

三、长寿互换定价解析式

最后，根据年金保险公司在长寿互换中的现金流特征来计算长寿互换的价格。借鉴Dowd et al.(2006)[7]的研究，年金保险公司对投资银行每年支付固定金额(1+π)Ht，其现值为年金保险公司从投资银行每年获得浮动金额Bt，其现值为为第t年的贴现因子。互换协议在签订之初对互换双方的价值均为零，所以固定现金流现值必须与浮动现金流现值相等，即因此，可得到长寿互换的价格π为：

不难看出，通过式(10)求解互换价格π的关键在于推导出经过Wang转换后的浮动现金流的期望值E*(Bt)，以下借鉴Lin and Cox(2005)[8]的研究，在长寿互换的现金流交换机制中加入生存率阈值这一触发条件，对E*(Bt)进行推导：

假设lx+1为x岁的目标人群第t年的实际随机生存概率；Xt为第t年生存率阈值，并假定有一个确定的生存率上限C。同时，假设年金保险公司出售的n份年金保单每份的年支付额m相同，所以当前所有年金支付总额为I=m×n，则可知年金保险公司在第t年的年金支付额为I×lx+1。当第t年的实际生存率lx+1大于阈值Xt时，年金保险公司根据互换协议从投资银行获得超出触发条件的年金支付额；当第t年的实际生存率lx+1达到并超过上限C时，年金保险公司可以获得一个固定的数额。

借鉴Lin and Cox(2005)[8]的研究，年金保险公司第t年从投资银行获得的浮动现金流Bt可表达为：

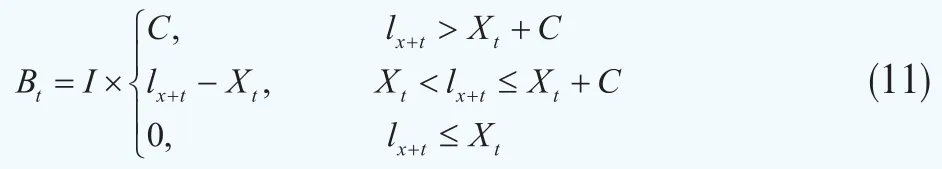
将上式右边的I移到左边，即可得到：

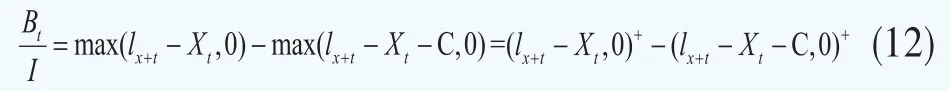
对上式两边求期望可得：

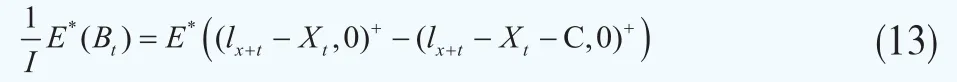
其中，lx+t为随机数，服从初始生存率lx与未来生存率t px的二项分布，由于lx是确定数值，因此lx+t的随机性来自于式(10)的t px。因此式(13)中的结果取决于经过Wang转换后的生存率即根据中心极限定理可知，当lx很大时lx+t的随机分布无限趋近正态分布。因此，当lx很大时，

由于给定随机变量X，且E(X)＜+∞，则有：

其中，F(x)=Pr(X≤x)。假设X服从标准正态分布，则式(14)可改写为：

φ(k)和Φ(k)很容易计算，并且由于lx+t近似服从正态分布近似服从标准正态分布。因此，利用式(16)和经过Wang转换后的参数μ*和σ*便能计算出

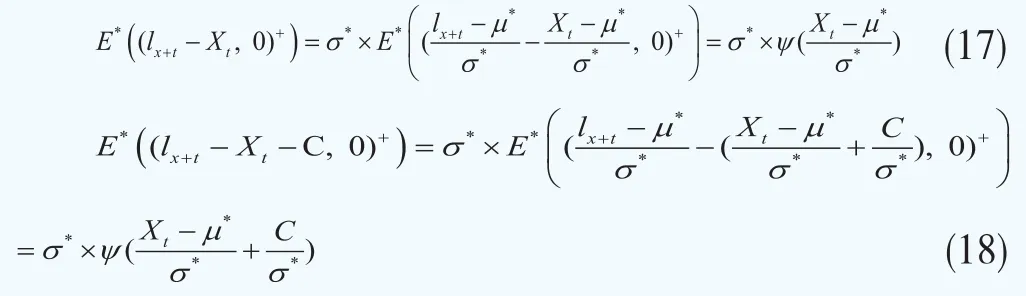
因此，将式(17)和式(18)代入式(13)整理可得第t年浮动现金流Bt经过Wang转换后的期望值为：

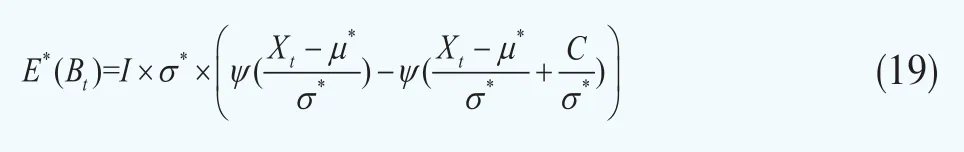
最后，将式(19)代入式(10)可得到长寿互换的价格为：

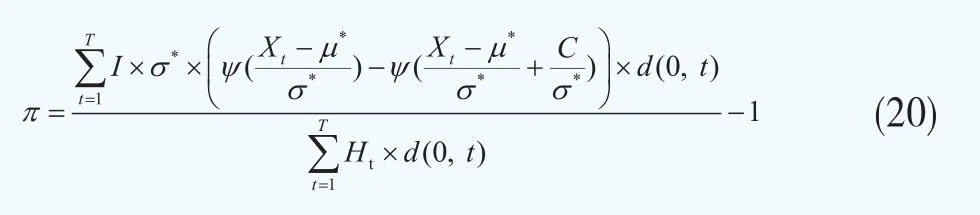
结语

长寿互换是一种双方协议，互换双方针对未来长寿风险规定一次性或定期交换现金流，并且至少有一方的现金支付额是变动的。通过触发机制，年金保险公司采用长寿互换可以有效地对冲所面临的长寿风险，从而能提高年金保险公司的承保能力。对长寿互换进行准确的定价，对长寿互换市场的发展至关重要。由于长寿互换市场的不完全性，不能采用传统金融工具的资本资产模型和无套利方法进行定价。目前国际上对长寿互换定价研究集中于不完全市场定价法——Wang转换定价法和风险中性定价法。

目前我国人口的平均寿命不断延长，人口老龄化问题日益严重。我国社保基金已出现大规模的亏空，延迟退休年龄或成为必然的选择。而寿险公司也将面临养老年金产品支付期大大延长的长寿风险。如何提高寿险公司的长寿风险管理能力，成为了亟待解决的重要问题。与长寿债券相比，长寿互换有一定的独特优势。因此如何开发适合我国国情的长寿互换产品，对于我国具有重大现实意义。本文系统分析了长寿互换的运行机制与定价方法，希望能够引起国内业界和学术界对长寿互换的关注与研究。