A NEW PROOF OF THE DELTA INEQUALITY∗

Yi QI（漆毅）Fei SONG（宋飞）

School of Mathematics and Systems Science，Beihang University，Beijing 100191，China

A NEW PROOF OF THE DELTA INEQUALITY∗

Yi QI（漆毅）Fei SONG（宋飞）

School of Mathematics and Systems Science，Beihang University，Beijing 100191，China

E-mail：yiqi@buaa.edu.cn；songfei19860810@163.com

The purpose of this paper is to give a relatively elementary and direct proof of the Delta Inequality，which plays a very important role in the study of the extremal problem of quasiconformal mappings.

Delta Inequality；Teichm¨uller space；quasiconformal mappings

2010 MR Subject Classification 30F60；32G15

1 Introduction

Let X be a Riemann surface whose universal covering surface is conformally equivalent to the unit disc D=｛z:|z|＜1｝on the complex plane C.By Bel（X）we denote the Banach space of Beltrami differentialsµ=µ（z）dz/dz on X with L∞-norms.

Let M（X）be the open unit ball in Bel（X）.For everyµ∈M（X），there is a quasiconformal mapping fµof X onto fµ（X），such that its Beltrami coefficient isµ.

Two elementsµand ν in M（X）are said to be Teichm¨uller equivalent，denoted byµ～ν，if there is a conformal mapping ϕ of fµ（X）onto fν（X）such that（fν）-1◦ϕ◦fµis homotopic to the identity of X（Mod∂X）.

The Teichm¨uller space T（X）is defined as the quotient space M（X）/～，or equivalently，T（X）is the space of Teichm¨uller equivalence classes［µ］ofµ∈M（X）.

As usual，Q（X）stands for the Banach space of integrable holomorphic quadratic differentials φ=φ（z）dz2on X with L1-norms

In the study of the extremal problem of quasiconformal mappings，the delta inequality plays a very important role（［5］，［1］and［6］，or see［3］also）.

Theorem A （Delta inequality）［3］Ifµand ν∈M（X）are in the same Teichm¨uller equivalent class with‖ν‖∞≤‖µ‖∞，then

for all φ∈Q（X）with‖φ‖=1，where M is a constant depends only on‖µ‖∞andµ1and ν1are the Beltrami coefficients of（fµ）-1and（fν）-1，respectively.

The above form of delta inequality was first appeared in［1］，which was used to solve the famous uniqueness problem of quasiconformal mappings.Recently，a generalized delta inequality is given in［4］as an application of the generalized main inequality of Reich-Strebel，which implies the delta inequality（1.1）in case of‖µ‖∞=‖ν‖∞.

The goal of this paper is to give a new and simple proof of the delta inequality（1.1）in general case directly from the main inequality of Reich-Strebel［7-9］，which is inspired by［4］.

Theorem B（the main inequality）［3］Suppose bothµand ν are two elements of M（X）andµ～ν.Then for any φ∈Q（X）with‖φ‖=1，we have

where ν1is the Beltrami coefficient of（fν）-1and

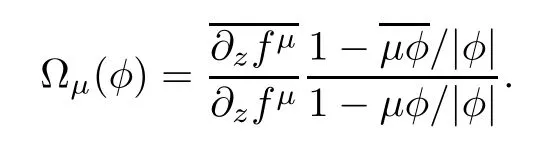
For the main inequality of Reich-Strebel we also refer［2］and［3］.

The paper is organized as follows.We give a lemma in§2 first and then we prove the Delta inequality in§3.

2 A Lemma

To prove Theorem A，we need the following lemma.

Lemma 2.1 has been appeared in［4］with constant 16 as the numerator in the right.For the sake of completeness and emphasizing the simplicity of our proof of the delta inequality，we give another proof of Lemma 2.1 here，which is more simple than the proof in［4］.

Proof A simple computation shows

which implies（2.1）directly.

3 Proof of the Delta Inequality

Since

it is clear that the delta inequality（1.1）is equivalent to the following inequality

Since‖ν‖∞≤‖µ‖∞，we have

So，in oder to get the delta inequality（1.1），we only need to prove

where C is a constant depending only on‖µ‖∞.

生：第一幅图旋转后得到图形是一个底面半径为6cm、高为12cm的圆柱挖去了一个底面半径6cm、高4cm的圆锥。

Proof Sinceµ～ν，by Theorem B，the main inequality（1.2）holds.

A simple computation shows

where Kµ=（1+‖µ‖∞）/（1-‖µ‖∞）.

Similarly，

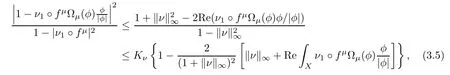
where Kν=（1+‖ν‖∞）/（1-‖ν‖∞）.

Then it follows from（1.2），（3.4）and（3.5）that

where

and

Noting the fact that both Lµand Λνare non-negative，it follows from（3.6）that

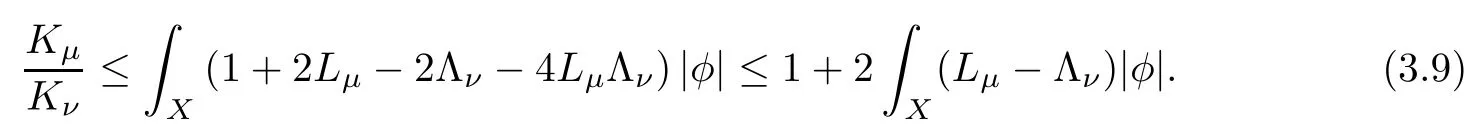
Putting（3.7）and（3.8）into（3.9），we have

and consequently，

Thus，

As‖ν‖∞≤‖µ‖∞，so it is easy to check that the algebraic sum of the first 3 tems in the right hand of（3.11）is nonpositive.Thus，by（3.11），we get

Since

so we have Z

By the definition of Ωµ，it is clear that

So

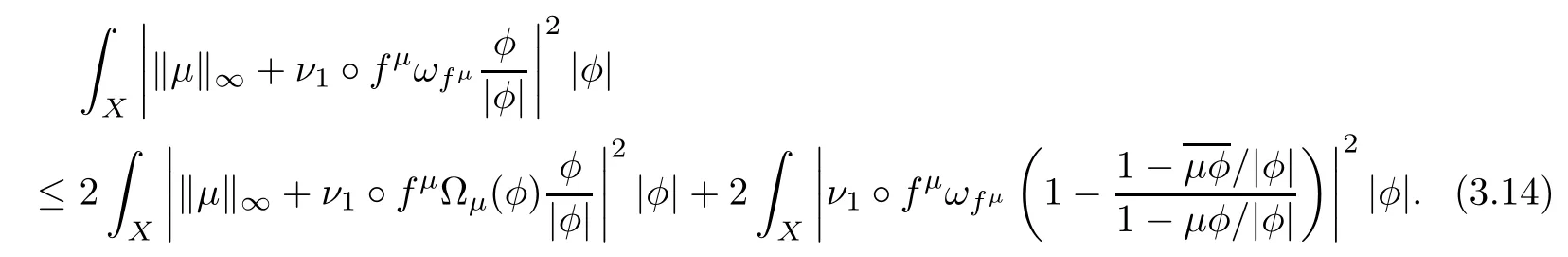
By Lemma 2.1，we have

As‖ν‖∞≤‖µ‖∞，

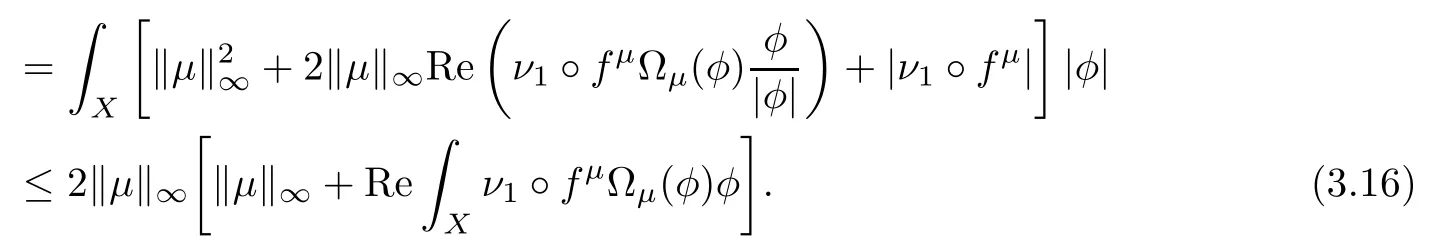
Therefore，（3.3）can be deduced from（3.13）-（3.16）and（3.12）.This completes the proof of the delta inequality.

［1］Boˇzin V，Lakic N，Markovi´c V，et al.Unique extremality.Journal d'Analyse Math´ematique，1998，75（1）: 299-338

［2］Gardiner F P.Teichm¨uller Theory and Quadratic Differentials.New York:John Wiley&Sons，1987

［3］Gardiner F P，Lakic N.Quasiconformal Teichm¨uller Theory.Amer Math Soc，2000

［4］Li Z，Qi Y.Fundamental inequalities of Reich-Strebel and triangles in a Teichm¨uller space.Contem Math，2012，575:283-297

［5］Reich E.On criteria for unique extremality of Teichm¨uller mappings.Ann Acad Sci Fenn Series A I Math，1981，（6）:289-301

［6］Reich E.The unique extremality counterexample.Journal d'Analyse Math´ematique，1998，75（1）:339-347

［7］Reich E，Strebel K.On quasiconformal mappings which keep the boundary points fixed.Trans Amer Math Soc，1969:211-222

［8］Reich E，Strebel K.Extremal plane quasiconformal mappings with given boundary values.Bull Amer Math Soc，1973，79（2）:488-490

［9］Strebel K.On quasiconformal mappings of open Riemann surfaces.Commentarii Mathematici Helvetici，1978，53（1）:301-321

∗Received November 18，2013.The research is partially supported by the National Natural Science Foundation of China（10971008 and 11371045）.