CONTROLLABILITY AND OPTIMALITY OF LINEAR TIME-INVARIANT NEUTRAL CONTROL SYSTEMS WITH DIFFERENT FRACTIONAL ORDERS∗
2015-11-21XiaoliDING丁小丽
Xiaoli DING(丁小丽)
Department of Mathematics,Xi'an Polytechnic University,Xi'an 710048,China
Juan J.NIETO
Departamento de An´alisis Matem´atico,Facultad de Matem´aticas,Universidad de Santiago de Compostela,15782,Santiago de Compostela,Spain Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia
CONTROLLABILITY AND OPTIMALITY OF LINEAR TIME-INVARIANT NEUTRAL CONTROL SYSTEMS WITH DIFFERENT FRACTIONAL ORDERS∗
Xiaoli DING(丁小丽)†
Department of Mathematics,Xi'an Polytechnic University,Xi'an 710048,China
E-mail:dingding0605@126.com
Juan J.NIETO
Departamento de An´alisis Matem´atico,Facultad de Matem´aticas,Universidad de Santiago de Compostela,15782,Santiago de Compostela,Spain Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia
E-mail:juanjose.nieto.roig@usc.es
Control systems governed by linear time-invariant neutral equations with different fractional orders are considered.Sufficient and necessary conditions for the controllability of those systems are established.The existence of optimal controls for the systems is given. Finally,two examples are provided to show the application of our results.
controllability;optimality;neutral equations;different fractional orders
2010 MR Subject Classification 26A33;33E12
1 Introduction
Fractional calculus was proved to be useful tools in the investigation of many phenomena in engineering,physics,economy,chemistry,electrodynamics of complex medium and other fields,see for instance[1-5].Many authors investigated the problem for different types of fractional differential equations,including fractional ordinary differential equations,fractional functional differential equations,fractional partial differential equations,and so on.
As one of the important topics in mathematical control theory,controllability plays an important role in the analysis and design of control systems.In recent years,the problem of controllability for various kinds of fractional differential equations was extensively studied by many researchers[6-15].The main tool employed in the analysis of controllability is based onan application of the fixed point theorem.However,the controllability results obtained by the fixed point theorem are inconvenient for computation in practical problems.
Inspired by the above-mentioned works,in this article,we follow the ideas in[9]to investigate the controllability of linear time-invariant neutral control systems with different fractional orders,and then give the optimality of such control systems.More precisely,we consider the following linear time-invariant neutral control system:
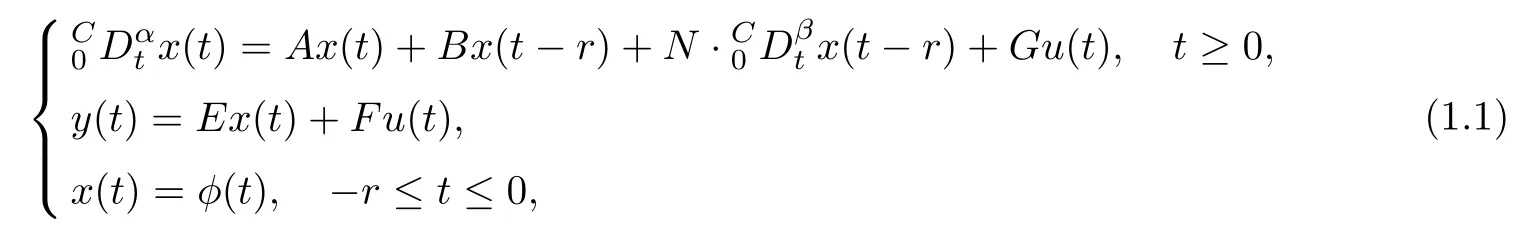
where A,B,N ∈Rn×n,G∈Rn×p,E ∈Rk×n,F∈Rk×p,0<β<α<1,state variable x(t)∈Rn,initial function φ(t)∈C([-r,0],Rn),and control input u(t)∈Rp.In fact,differential equations with different fractional orders often arise in many physical and engineering models,see[16-25].So it is necessary to study the controllability and optimality of the neutral control systems with different fractional orders.
This article is organized as follows.In Section 2,we briefly review the definitions of fractional calculus.We present the concept of controllability for the linear time-invariant neutral control systems with different fractional orders.In Section 3,we give the sufficient and necessary conditions for the controllability of the control systems.In Section 4,we discuss the existence of optimal control.In Section 5,the applicability of the presented theory is demonstrated with two examples,and Section 6 briefly summarizes the results of this article.
2 Preliminaries
In this section,we give some basic definitions and results that are used throughout this article.For more details,please see[26,27].
Definition 2.1 Let[a,b]be a finite interval on the real axis R.The fractional integral of order α>0 with the lower limit a for the function x is defined asprovided the right-hand side is pointwise defined on[a,b],where Γ(·)is the Gamma function.
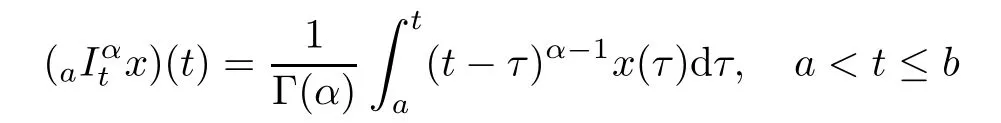
Definition 2.2 Let[a,b]be a finite interval on the real axis R,n-1<α≤n,n∈N+. And let the function x(t)have continuous derivatives up to order n such that x(n)(t)is absolutely continuous on[a,b].The Caputo fractional derivative(CaDαtx)(t)of order α is defined as
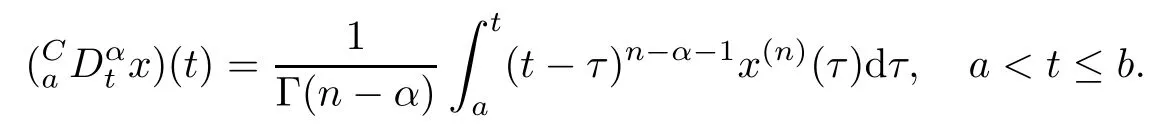
The Laplace transform of the Caputo's fractional derivative)is
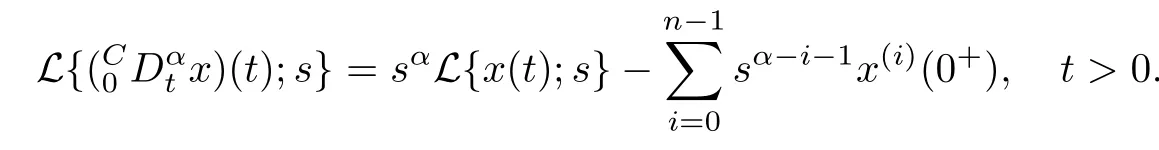
Definition 2.3 The two-parameter Mittag-Leffler function is defined as
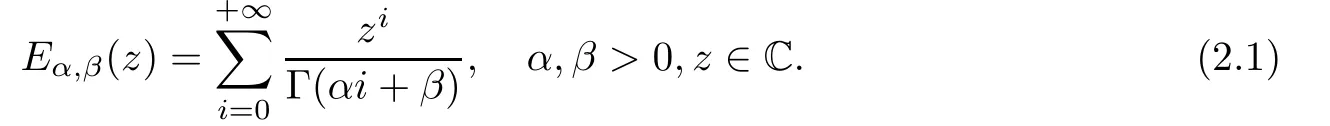
The Laplace transform of the two-parameter Mittag-Leffler function is
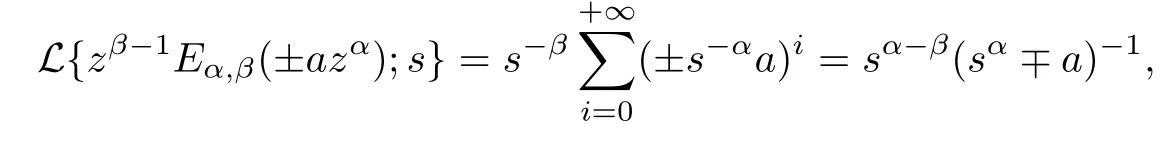
provided that|s-βa|<1.
In addition,the Laplace transform of tα-1is

Lemma 2.1 Let 0<β<α<1.Then it holds
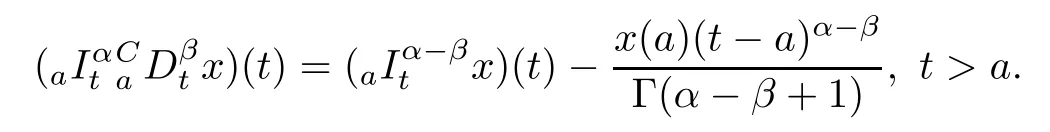
Proof According to the definitions of the operatorsand,we have
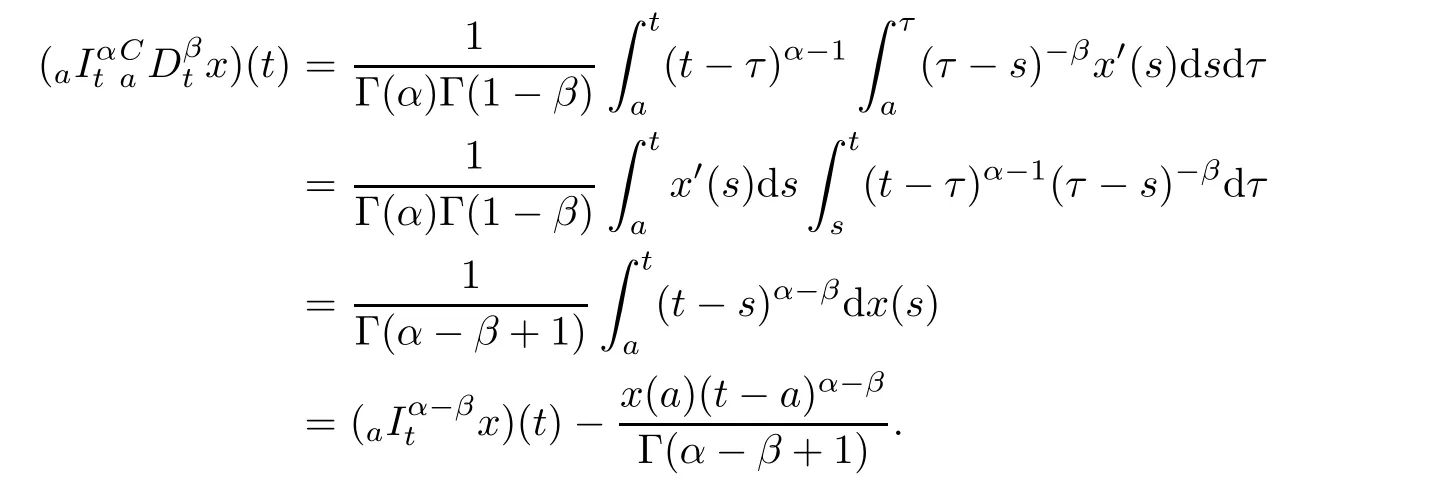
The proof is completed.
3 Controllability
Definition 3.1 System (1.1)is said to be controllable if for every continuous initial function φ,there exists a control u∈C([0,T])such that the solution x(t)of system(1.1)satisfies x(t1)=0,for some t1>0.
First,we give a useful lemma.
Lemma 3.1 If x(t)is a solution of system(1.1),then x(t)satisfies the following integral equation
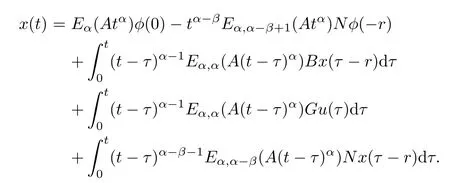
Proof By Lemma 2.1,system(1.1)is equivalent to the integral equation
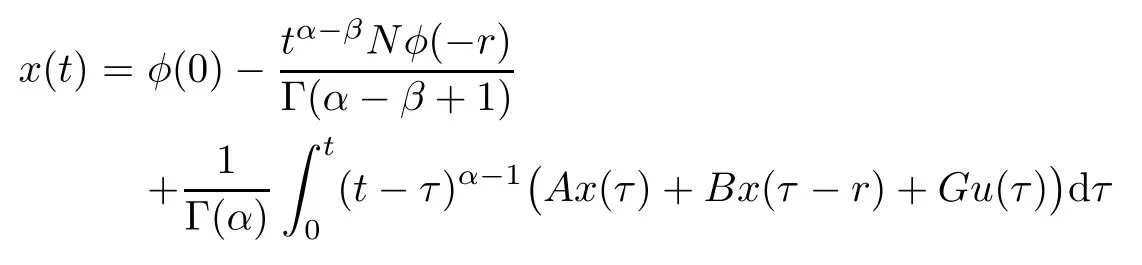
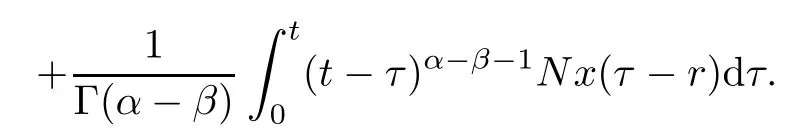
Taking the Laplace transform on the both-side of the above equality,we obtain
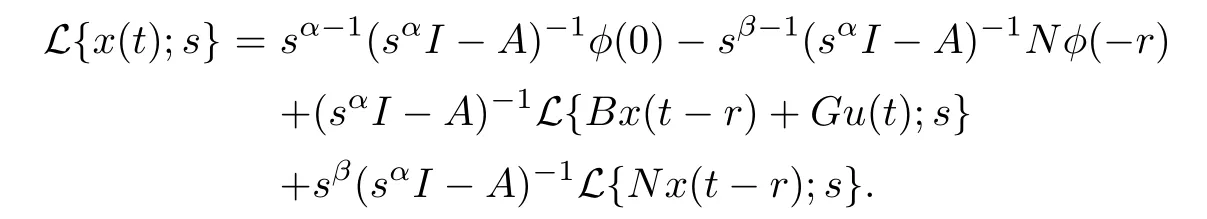
Applying the Laplace inverse transform and convolution theorem leads to
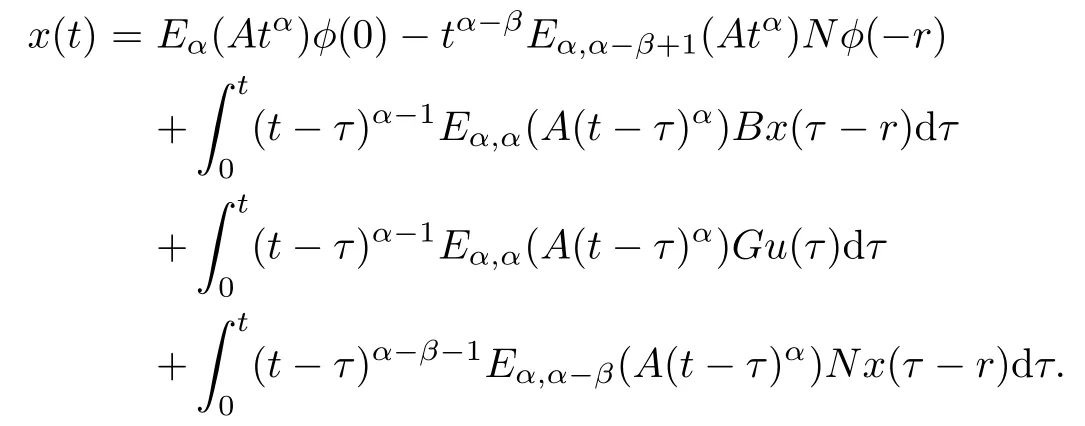
The proof is completed.is nonsingular for some tf∈(0,+∞),where·Tdenotes the matrix transpose.
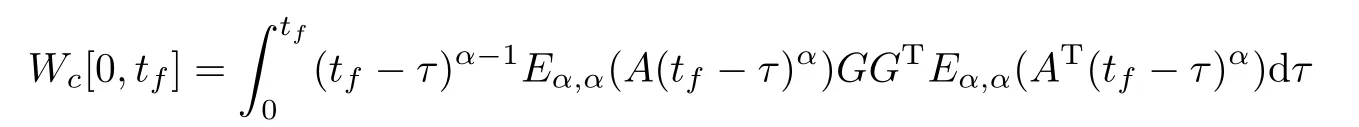
Proof Sufficiency.Suppose that the matrix Wc[0,tf]is nonsingular,then W-1c[0,tf]exists.For any φ(t)∈C([-r,0],Rn),we take the control input u(t)as
Now we state the sufficient and necessary condition for the controllability.
Theorem 3.1 System(1.1)is controllable on[0,tf]if and only if the Gramian matrixBy Lemma 3.1,it is elementary to verify that x(tf)=0.Thus,system(1.1)is controllable on[0,tf].

Necessity.Suppose system(1.1)is controllable.Now we prove that the matrix Wc[0,tf]is nonsingular.In fact,if Wc[0,tf]is singular,there exists a nonzero vector z0such that

That is
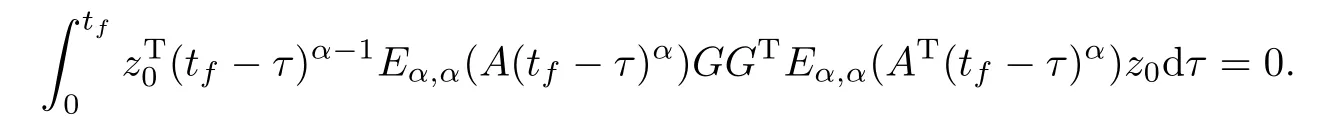
This implies that,for all τ∈[0,tf],it has

Since system(1.1)is controllable,there exist control inputs u1(t)and u2(t)such that
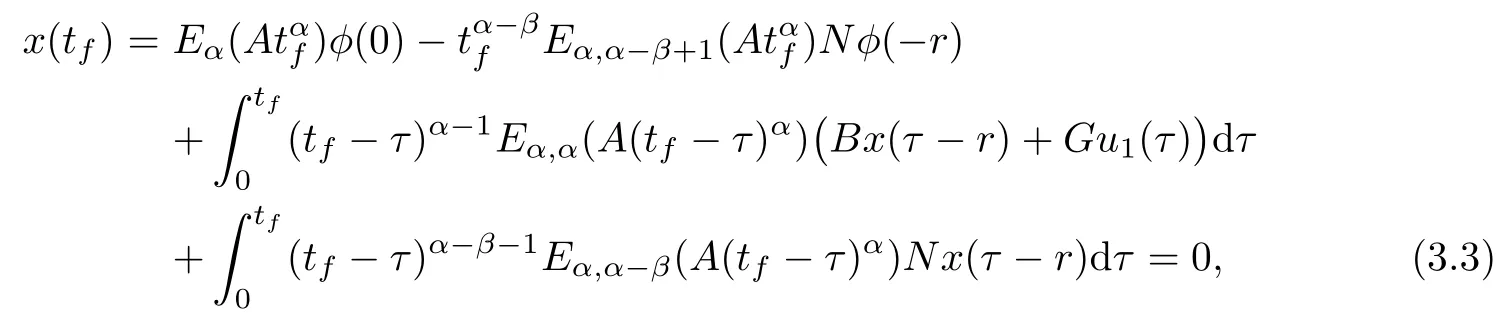
and
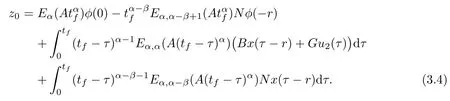
Subtracting(3.3)from(3.4)leads to

Furthermore,multiplying zT0on the both sides of(3.5)we have

Combining(3.2),we get zT0z0=0.Thus z0=0,which contradicts z0/=0.The proof is completed. □
Based on Theorem 3.1,we can obtain another characterization of the controllability.
Theorem 3.2 System(1.1)is controllable on[0,tf]if and only if

Proof By the Cayley-Hamilton theorem,there exist constants a0,a1,···,an-1such that
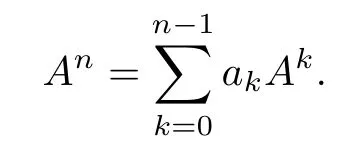
So there exist polynomials ck(t)(k=0,1,···,n-1)with respect to t such that
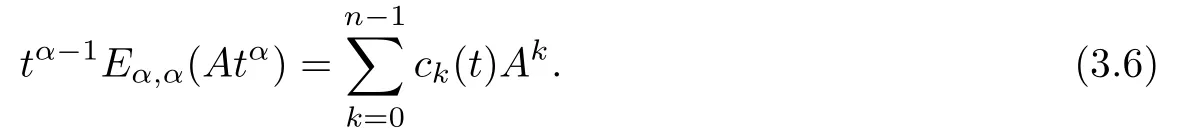
It follows that
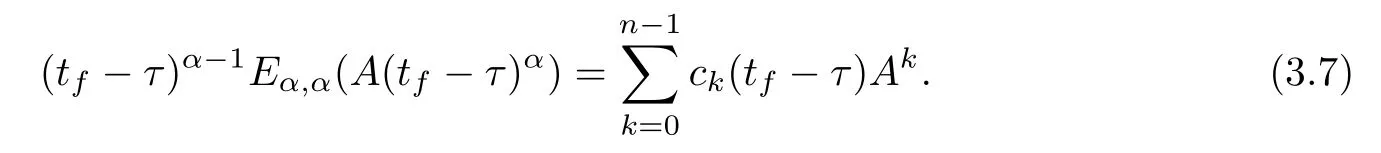
We denote Q as
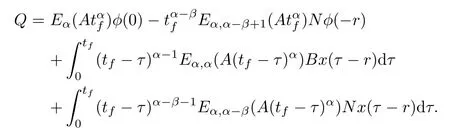
Then,by Lemma 3.1,we have
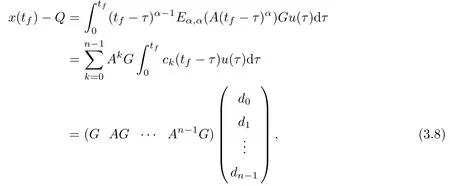
4 Existence of Optimal Controls
In this section,we discuss the existence of optimal controls of system(1.1).
According to Lemma 3.1,we can prove the following theorem.
Theorem 4.1 System(1.1)has a unique solution x(t)corresponding to u given by
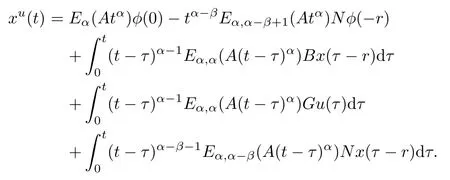
Proof It is trivial to demonstrate the fact since we may explicitly calculate the solution by the method of steps.In fact,on the interval[0,r],xu(t)is uniquely determined by

Once xu(t)is known on[0,r]and since it is continuous on this interval,one can use the solution xu(t)on[0,r]to obtain xu(t)on[r,2r].The process can be continued to prove this theorem.
We suppose that Y is another separable reflexive Banach space from which the controls u take the value.We denote a class of nonempty closed and convex subsets of Y by W(Y).Themultifunction ω:[0,+∞)→W(Y)is continuous and ω(·)⊂V,where V is a bounded set of Y,the admissible control set Uad={u∈C(V)|u(t)∈ω(t)}.Then Uadis nonempty.
We consider the Bolza Problem(P):
Find u0∈Uadsuch that

where the performance function J is defined as

As usual,if u0exists,then(x0,u0)is called an optimal pair,where x0is the solution of system(1.1)corresponding to u0.
To study the existence of optimal controls,we require the following assumptions:
(HL1)The functional l:[0,+∞)×C([0,+∞))×Y→R∪{∞}is Borel measurable.
(HL2)The functional l(t,·,·)is sequentially lower semicontinuous on C([0,+∞))×Y for almost all t∈[0,+∞).
(HL3)The functional l(t,x,·)is convex on Y for each x∈C([0,+∞))and almost all t∈[0,+∞).
(HL4)There exist constants b≥0,c>0,and a nonnegative function g(t)∈C([0,+∞))such that
l(t,x,u)≥g(t)+b‖x‖+c‖u‖for all x∈C([0,+∞)),u∈Uad.
Now we state the existence result of optimal controls for system(1.1).
Theorem 4.2 Suppose that assumptions(HL1)-(HL4)are fulfilled.Then system(1.1)has at least one optimal pair.
Proof If inf{J(u)|u∈Uad}=+∞,then there is nothing to prove. Assume that inf{J(u)|u∈Uad}=ρ<+∞.By assumption(HL4),we have ρ>-∞.Therefore there exists a sequence{um}⊂Uadsuch that J(um)→ρ as m→+∞.Since{um}is bounded in the space Uad,there exists a subsequence,relabeled as{um},and u0∈C([0,+∞),Y)such that um⇀u0in C([0,+∞),Y),where the symbol‘⇀'stands for weakly convergence.Moreover,since Uadis closed and convex,by Marzur lemma,u0∈Uad.
Suppose that xmis the solution of system(1.1)corresponding to um,and x0is the solution of system(1.1)corresponding to u0.Then xmand x0satisfy the following equation,respectively,
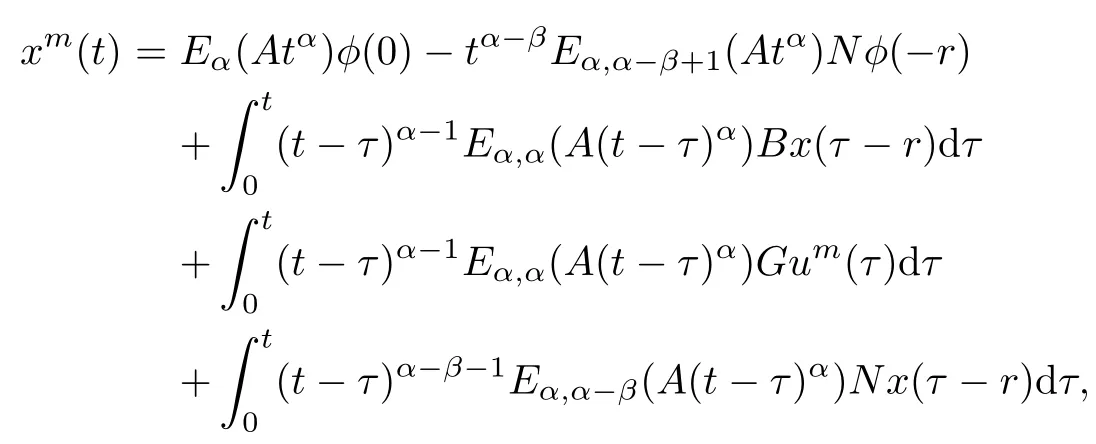
and
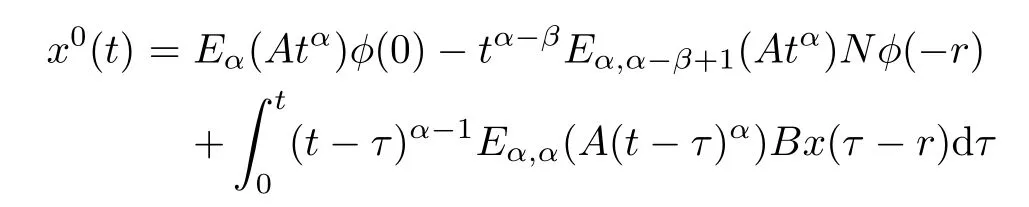
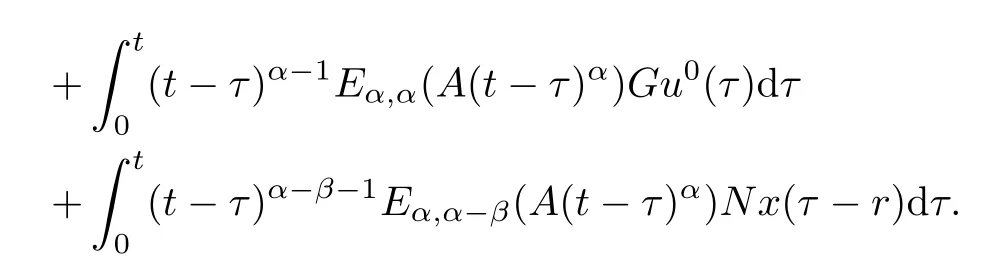
First,we consider the case t∈[0,r].Note that,in this case,xm(t)=x0(t)=φ(t).Then

Since um⇀u0,and the operator R is compact(see Property 2.1 of[28]),we have

For the case t∈[r,2r],we have

On the other hand,combining(4.1),we get
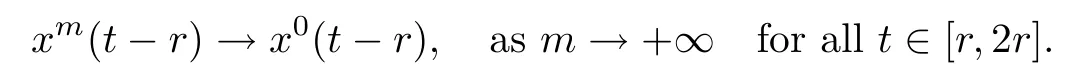
Also since um⇀u0,and the operator R is compact,we obtain that

By the method of steps,we deduce that
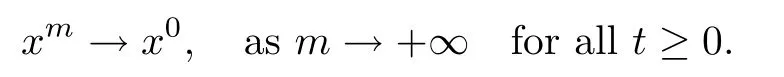
Using the assumption and the Balder's theorem,we can obtain that

which implies that J reaches its minimum atThe proof is completed.
5 Applications
In this section,we consider two examples of linear time-invariant neutral control systems with different fractional orders.
Example 5.1 Consider system(1.1).We choose α=12,β=13,and
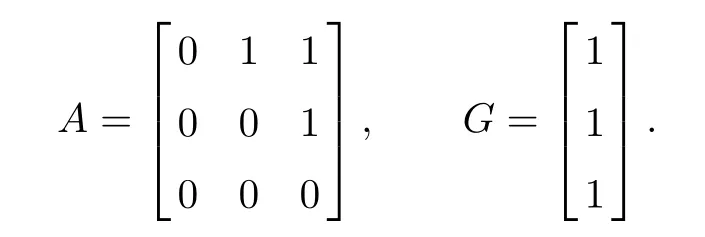
Now we apply Theorem 3.1 to prove system(1.1)is controllable.First,
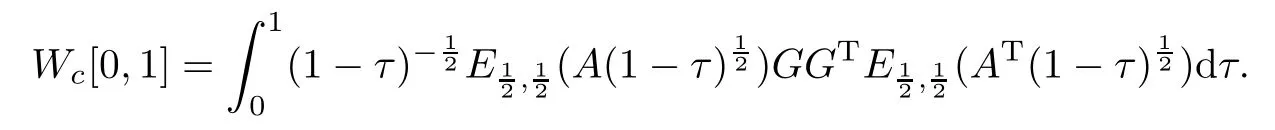
By computation,we obtain
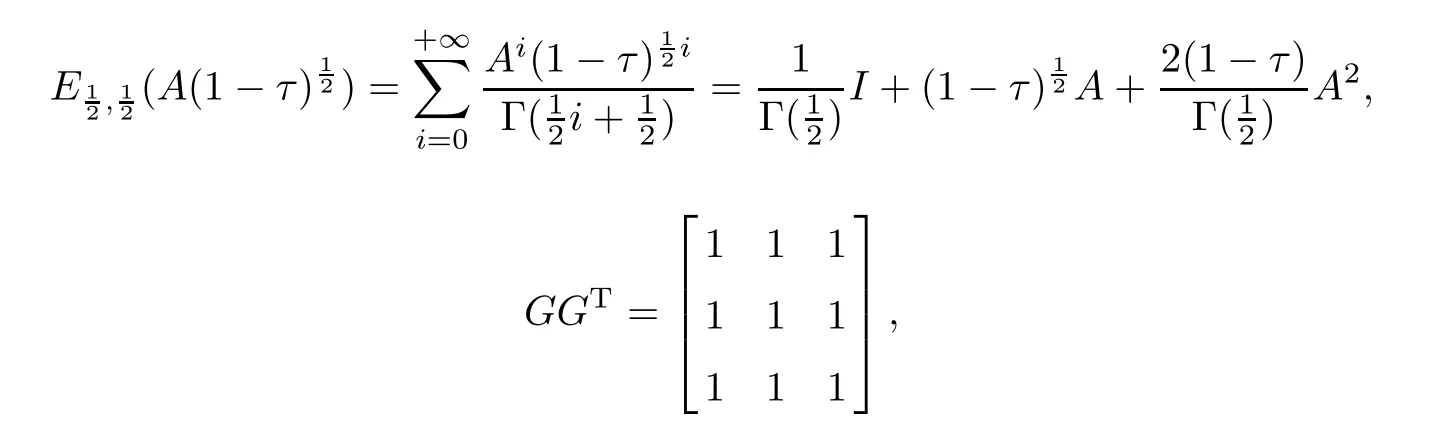
and

One can see that the matrix Wc[0,1]is nonsingular.Thus,system(1.1)is controllable.
Example 5.2 Consider system(1.1).We choose α=12,β=13,and
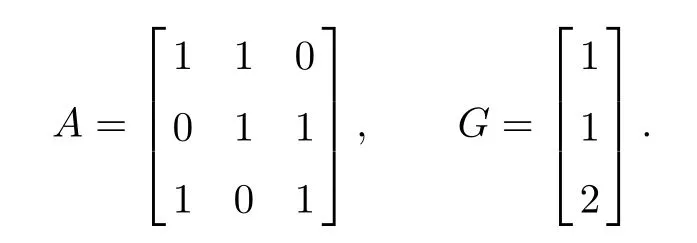
Now we apply Theorem 3.2 to prove system(1.1)is controllable.By computation,we obtain
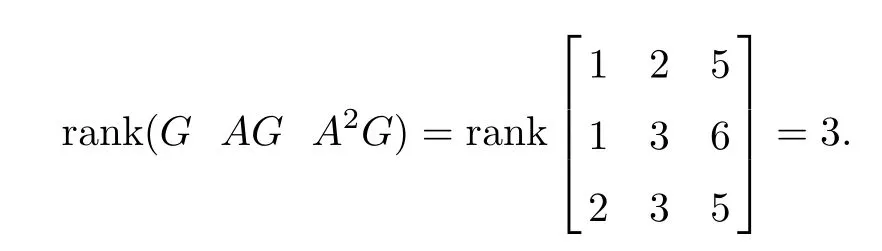
Thus,by Theorem 3.2,system(1.1)is controllable.
For the above two examples,original systems have optimal control pairs.In fact,we can define the performance function J as
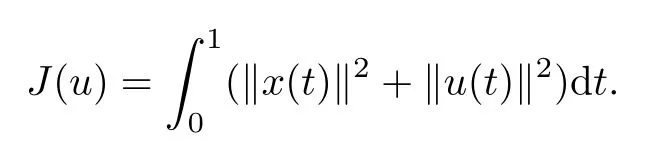
It is obvious to check that J(u)satisfies the assumptions in Theorem 4.1.Thus,the two systems have optimal control pairs.
6 Conclusions
Sufficient and necessary conditions for the controllability of linear time-invariant neutral control systems with different fractional orders have been presented.The existence of optimalcontrols for such systems has been proved.The presented theory has been applied to two examples.
[1]Hilfer R.Applications of Fractional Calculus in Physics.Singapore:World Scientific,2000
[2]Vasilyeva O,Lutscher F.Competition of three species in an advective environment.Nonlinear Anal RWA,2012,13:1730-1748
[3]Cesbron L,Mellet A,Trivisa K.Anomalous transport of particles in plasma physics.Appl Math Lett,2012,25:2344-2348
[4]Metzler R,Klafter J.The random walk's guide to anomalous diffusion:a fractional dynamics approach. Phys Rep,2000,339:1-77
[5]Postnikov E B,Sokolov I M.Model of lateral diffusion in ultrathin layered films.Phys A,2012,391: 5095-5101
[6]Agarwal R P,Baghli S,Benchohra M.Controllability for semilinear functional and neutral functional evolution equations with infinite delay in Fr´echet spaces.Appl Math Optim,2009,60:253-274
[7]Wang J R,Zhou Y.Existence and controllability results for fractional semilinear differential inclusions. Nonlinear Anal RWA,2011,12:3642-3653
[8]Wang J R,Zhou Y.A class of fractional evolution equations and optimal controls.Nonlinear Anal RWA,2011,12:262-272
[9]Zhou X F,Wei J,Hu L G.Controllability of a fractional linear time-invariant neutral dynamical system. Appl Math Lett,2013,26:418-424
[10]Sakthivel R,Mahmudov N I,Nieto J J.Controllability for a class of fractional-order neutral evolution control systems.Appl Math Comput,2012,218:10334-10340
[11]Balachandran K,Zhou Y,Kokila J.Relative controllability of fractional dynamical systems with delays in control.Commun Nonlinear Sci Numer Simul,2012,17:3508-3520
[12]Tai Z,Lun S.On controllability of fractional implulsive neutral infinite delay evolution integrodifferential systems in Banach spaces.Appl Math Lett,2012,25:104-110
[13]Butkovskii A G,Postnov S S,Postnova E A.Fractional integro-differential calculus and its controltheoretical applications,II,fractional dynamic systems:modeling and hardware implementation.Autom Remote Control,2013,5:725-749
[14]Balachandran K,Govindaraj V,Rodr´ıguez-Germ´a L,Trujillo J J.Controllability of nonlinear higher order fractional dynamical systems.Nonlinear Dynam,2013,1:33-43
[15]Debbouche A,Baleanu D.Controllability of fractional evolution nonlocal impulsive quasilinear delay integro-differential systems.Comput Math Appl,2011,62:1442-1450
[16]¨Ozdemir N,Karadeniz D,˙Iskender B B.Fractional optimal control problem of a distributed system in cylindrical coordinates.Phys Lett A,2009,373:221-226
[17]Vinagre B M,Monje C A,Calderon A J.Fractional order systems and fractional order control actions. 41th IEEE Conf Decision Control,Las Vegas,NV,Dec.2002
[18]Cai X,Liu F.Numerical simulation of the fractional-order control system.J Appl Math Comput,2007,23: 229-241
[19]Deng W H,Li C P,Guo Q.Analysis of fractional differential equations with multi-orders.Fractals,2007,15:173-182
[20]Zhang L H,Ahmad B,Wang G T.The existence of an extremal solution to a nonlinear system with the right-handed Riemann-Liouville fractional derivative.Appl Math Lett,2014,31:1-6
[21]Bashir A,Nieto J J,Ahmed A.Existence and uniqueness of solutions for nonlinear fractional differential equations with non-separated type integral boundary conditions.Acta Math Sci,2011,31B:2122-2130
[22]Li N,Wang C Y.New existence results of positive solution for a class of nonlinear fractional differential equations.Acta Mathematica Scientia,2013,33B:847-854
[23]Wang G T,Liu S Y,Zhang L H.Neutral fractional integro-differential equation with nonlinear term depending on lower order derivative.J Comput Appl Math,2014,260:167-172
[24]Kaczorek T.Positive linear systems consisting of n subsystems with different fractional orders.IEEE Trans Circuits Syst I,2011,58:1203-1210
[25]Ahmad B,Nieto J J,Alsaedi A,El-Shahed M.A study of nonlinear Langevin equation involving two fractional orders in different intervals.Nonlinear Anal RWA,2012,13:599-606
[26]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies,204.Amsterdam:Elsevier Science BV,2006
[27]Podlubny I.Fractional Differential Equations.New York:Academic Press,1999
[28]Ding X L,Jiang Y L.Semilinear fractional differential equations based on a new integral operator approach. Commun Nonlinear Sci Numer Simul,2012,17:5143-5150
[29]Balder E J.Necessary and sufficient conditions for L1-strong-weak lower semicontinuity of integral functionals.Nonlinear Anal TMA,1987,11:1399-1404
Appendix
In this section,we give the Balder's theorem(Theorem 2.1,[29]),which is used in Section 4.
Let(T,J,µ)be a finite nonatomic measure space,(X,‖‖)a separable Banach space,and(V,|·|)a reflexive separable Banach space,whose dual we denote by V′.Let f:T×X×V→(-∞,+∞]be a given J×B(X×V)-measurable function.The associated integral functional If:L1X×L1V→[-∞,+∞]is defined by

Theorem A.1(Balder's theorem)The following three conditions
f(t,·,·)is sequentially l.s.c.on X×Vµ-a.e.,
f(t,·,·)is convex on V for every on x∈Xµ-a.e.,there exits M>0 and ψ∈L1Rsuch that
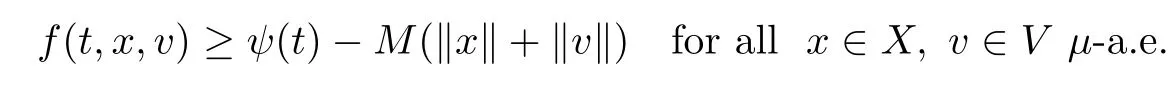
are sufficient for sequential strong-weak lower semicontinuity of Ifon L1X×L1V.Moreover,they are also necessary,provided that If(x,v)<+∞for some x∈L1X,v∈L1V.
∗Received May 13,2014;revised July 27,2014.The first author is supported by the Science and Technology Planning Project(2014JQ1041)of Shaanxi Province and the Scientic Research Program Funded by Shaanxi Provincial Education Department(14JK1300)and the Research Fund for the Doctoral Program(BS1342)of Xi'an Polytechnic University.The second author is partially supported by Ministerio de Econom´ıay Competitividad and EC fund FEDER,Project no.MTM2010-15314,Spain.
†Corresponding author:Xiaoli DING.
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ALL MEROMORPHIC SOLUTIONS OF AN AUXILIARY ORDINARY DIFFERENTIAL EQUATION AND ITS APPLICATIONS∗
- APPROXIMATION OF COMMON FIXED POINT OF FAMILIES OF NONLINEAR MAPPINGS WITH APPLICATIONS∗
- SOME COMPLETELY MONOTONIC FUNCTIONS ASSOCIATED WITH THE q-GAMMA AND THE q-POLYGAMMA FUNCTIONS∗
- SUB-ADDITIVE PRESSURE ON A BOREL SET∗
- AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
- ORBITAL INSTABILITY OF STANDING WAVES FOR THE GENERALIZED 3D NONLOCAL NONLINEAR SCHR¨ODINGER EQUATIONS∗
