Lp-CONTINUITY OF NONCOMMUTATIVE CONDITIONAL EXPECTATIONS∗

Jian HU（胡建）Congbian MA（马聪变）Youliang HOU（侯友良）

School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China

Lp-CONTINUITY OF NONCOMMUTATIVE CONDITIONAL EXPECTATIONS∗

Jian HU（胡建）Congbian MA（马聪变）†Youliang HOU（侯友良）

School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China

E-mail:hujian279@163.com；macongbian@126.com；ylhou323@whu.edu.cn

Let（M，τ）be a noncommutative probability space，（Mn）n≥1a sequence of von Neumann subalgebras of M and N a von Neumann subalgebra of M.We introduce the notions ofµ-approach and orthogonal approach for（Mn）n≥1and prove that E（x|Mn）Lp--→E（x|N）for any x∈Lp（M）（1≤p＜∞）if and only if（Mn）n≥1τ-approaches and orthogonally approaches N.

von Neumann algebra；trace；conditional expectation；orthogonal approach

2010 MR Subject Classification 46L51；46L52

1 Introduction

The theory of noncommutative Lp-spaces has a long history going back to pioneering works by von Neumann and Schatten［9］，Dixmier［7］and Segal［6］.Replacing the the integral of a function by the trace of a matrix or an operator，the noncommutative Lp-spaces are composed of the elements whose p-th power has finite trace.On the one hand，noncommutative Lp-spaces share many properties with usual Lp-spaces（commutative Lp-spaces），on the other hand，they are very different from the later.Some tools in the study of usual commutative Lp-spaces still work in the noncommutative setting.However，most of the time，we need new techniques. Since the nineties of the last century，some new theories such as those of operator spaces and free probability stimulate the new developments.In particular，noncommutative Khintchine and martingale inequalities［5］opened new perspectives.It is well known nowadays that the theory of noncommutative Lp-spaces is intimately related with many other fields such as Banach spaces，operator algebras，operator spaces，quantum probability and noncommutative harmonic analysis.

In this paper，we focus on the Lp-continnuity of noncommutative conditional expectations. To ease its understanding we recall the classical setting.Let（Ω，F，µ）be a probability space andan increasing filtration of σ-subalgebras ofBy Levi's theorem，for anyand 1≤p＜∞we have.In otherwords，if G is a σ-subalgebras of F，then a sufficient condition for）is thatis increasing andSome examples given by Alonso［1，2］showed the conditions is not necessary.In seeking for the necessary and sufficient conditions，Alonso introduced the notions ofµ-approach and orthogonal approach for（Fn）n≥1and proved that E（f|Fn）-L-→pE（f|G）if and only if（Fn）n≥1µ-approaches and orthogonally approaches G.By the result，we can deduce Levi's theorem.We turn to noncommutative setting.Let（M，τ）be a noncommutative probability.We know that if（Mn）n≥1is an increasing sequence and N is the von Neumann algebra generated，thenfor any x∈Lp（M），where 1≤p＜∞（see［10］）.Similarly，the conditions of the result is not necessary.Inspired by Alonso［1，2］，we introduce the τ-approach and orthogonal approach for（Mn）n≥1and prove that ε（x|Mn）Lp--→ε（x|N）if and only if（Mn）n≥1τ-approaches and orthogonally approaches N.

2 Preliminaries

We recall some necessary preliminaries on non-commutative Lp-spaces.The readers are referred to［5］for details.

Given a（complex）Hilbert space H we denote by B（H）the space of all bounded linear operators on H equipped with the operator norm.The identity operator on H is denoted by 1.Recall that a von Neumann algebra M is a C∗-subalgebra of B（H）which contains 1 and is closed with respect to the weak operator topology.The positive cone of M is denoted by M+. A trace on M is a map τ:M+→［0，∞］satisfying

（i）τ（x+y）=τ（x）+τ（y），∀x，y∈M+；

（ii）τ（λx）=λτ（x），∀λ∈［0，∞），x∈M+；

（iii）τ（u∗u）=τ（uu∗），∀u∈M.

τ is said to be normal if τ（supαxα）=supατ（xα）for any bounded increasing net｛xα｝in M+，and faithful if for any x∈M+，τ（x）=0 implies x=0.If τ（1）＜∞，τ is said to be finite. In the sequel，unless explicitly stated otherwise τ will always denote a normal faithful finite trace.We will always assume that τ is normalized，that is，τ（1）=1.In this case we think of τ as a non-commutative probability and call（M，τ）a non-commutative probability space.Let L0（M）denote the topological∗-algebra of all measurable operators with respect to（M，τ）. The trace τ can be extended to the positive cone L+0（M）of L0（M）.For 1≤p≤∞，let Lp（M）be the associated noncommutative Lp-space.Recall that for 1≤p＜∞，the norm on Lp（M）is defined by

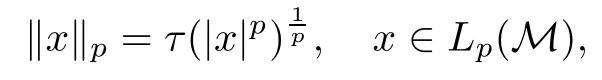
（i）τ（ε（x））=τ（x），x∈Lp（M）；

（ii）εN（axb）=aεN（x）b，a∈Lp（N），x∈Lq（M），b∈Lr（N），

where 1≤p，q，r≤∞，p-1+q-1+r-1≤1.We call εNthe conditional expectation of N and denoted by ε（·|N）.

In this paper（Mn）n≥1will always denote a sequence of von Neumann subalgebras of M and N a von Neumann subalgebra of M.For any x∈L1（M），let εn（x）be the conditional expectation of x with respect to Mnand εN（x）be the conditional expectation of x with respect to N.We use P（M）to denote the lattice of projections in M.

3 Main Results and Proofs

The first result of this section asserts that if we restrict ourselves to x∈Lp（N），then the conditional expectations εn（x）converge in Lp（M）if and only if（Mn）n≥1τ-approaches N.We start by introducing the definition of τ-approach.

Definition 3.1 We will say that（Mn）n≥1τ-approaches N（denoted as Mnτ-→N），if for each e∈P（N），there existsuch that

Proof The proof of Theorem 3.2 is divided into three steps.

Consider first the case p=2.By the traciality of τ，we get that

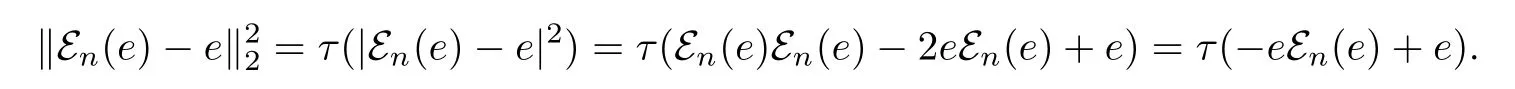
We need to extend this result to 1≤p＜∞.If 2＜p＜∞，using the inequality‖|εn（e）-we get

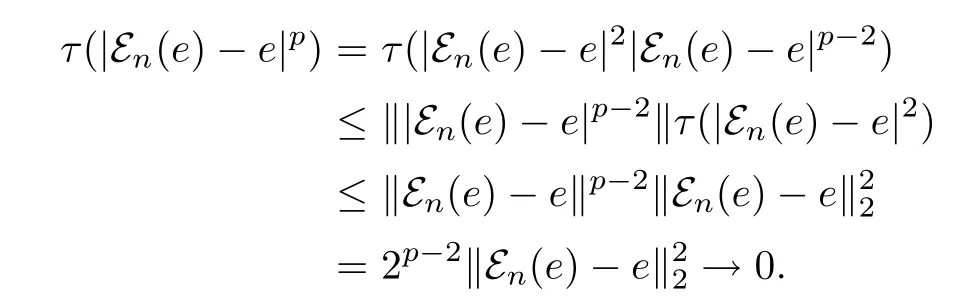
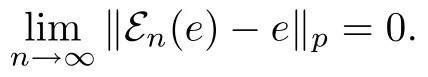
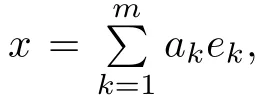
By hypothesis，for any e∈P（N）we have thatthen en∈P（Mn）.Note that τ（1）=1，we have

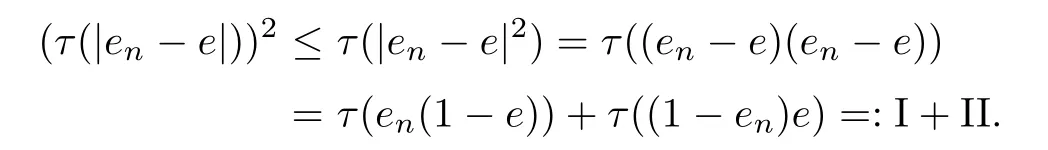
Combining the preceding estimates，we obtain τ（|en-e|）→ 0.Therefore，The theorem is proved.

Proof Let x∈Lp（M∞）and xn=εn（x），then the sequence（xn）n≥1is a martingale.By the convergence theorem for noncommutative martingales，we have that εn（x）Lp（M）----→x，where 1≤p＜∞.By Theorem 3.2.we get that Mnτ-→M∞.This completes the proof. □

Let N be a von Neumann subalgebra of M.Set ε⊥N=1-εN.We call ε⊥Nthe orthogonal conditional expectation induced by N.The name arises since，for p=2，ε⊥Nis the orthogonal projection from L2（M）to L2（N）⊥.

Definition 3.4 We will say that（Mn）n≥1approaches orthogonally to N （denoted as Mn

⊥-→N），if for any sequence｛en｝n≥1，where en∈P（Mn），it holds that ε⊥N（en）w-→0 in L2（M）（i.e.for any x∈L2（M），<ε⊥N（en），x>→0）.

Given a sequence（Mn）n≥1of von Neumann subalgebras of M，there can be many different von Neumann subalgebras of M such that（Mn）n≥1orthogonally approaches them.For example，any sequence（Mn）n≥1orthogonally approaches M.We will be interested in the minimum of such von Neumann subalgebras.

Definition 3.5 Define M⊥as the set of elements x∈L2（M）such that there is a subsequence（Mnk）of（Mn）and enk∈P（Mnk）（k≥1）with the property that

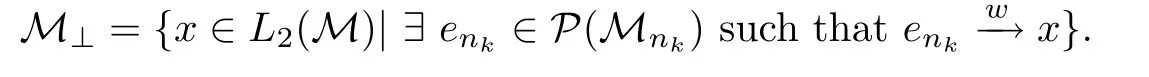
We now state the main result of this paper.

For the proof of the theorem we need to prove several lemmas first.

Lemma 3.7 Mn⊥-→N iff M⊥⊂L2（N）.

It is clear that f is a continuous linear functional on L2（M）.Thus we deduce

Combining（3.1），（3.2），we obtain

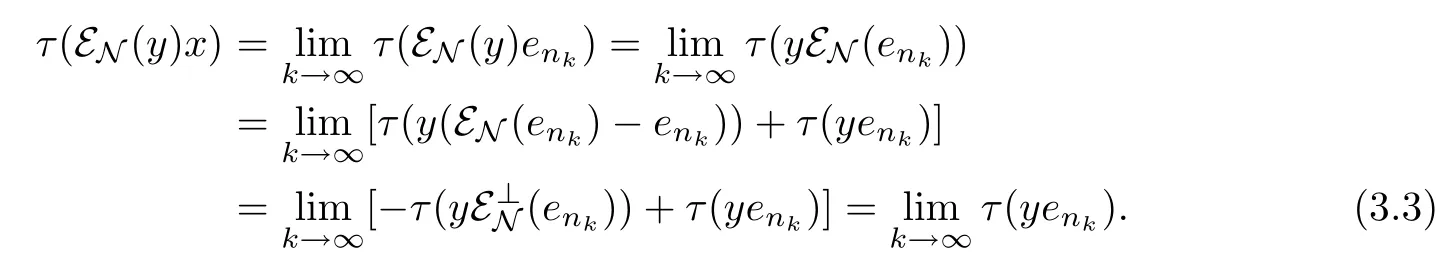
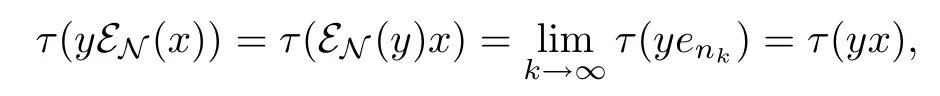
whence τ（y（εN（x）-x））=0（y∈L2（M））.Set y=（εN（x）-x）∗，we get τ（|εN（x）-x|2）=0. Therefore，x=εN（x）∈L2（N）.Thus M⊥⊂L2（N）.

Conversely，assume that M⊥⊂L2（N）and suppose that Mndoes not approaches orthogonally to N.Then there exists en∈P（Mn）such that ε⊥N（en）does not converges weakly to 0. By duality，there exists x∈L2（M）such that τ（x∗ε⊥N（en））→0.Thus there exist a constant ε0＞0 and a subsequence｛enk｝of｛en｝such that

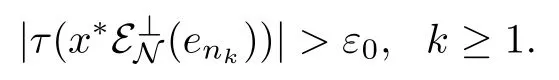
Since｛enk｝is bounded in L2（M）and L2（M）is reflexive，it has a subsequence，which we will also denote by｛enk｝，converges weakly to a element y in L2（M）.This means y∈M⊥by the definition of M⊥.By hypothesis M⊥⊂L2（N），we know that y∈L2（N）and hence εN（y）=y. Because that，we have that

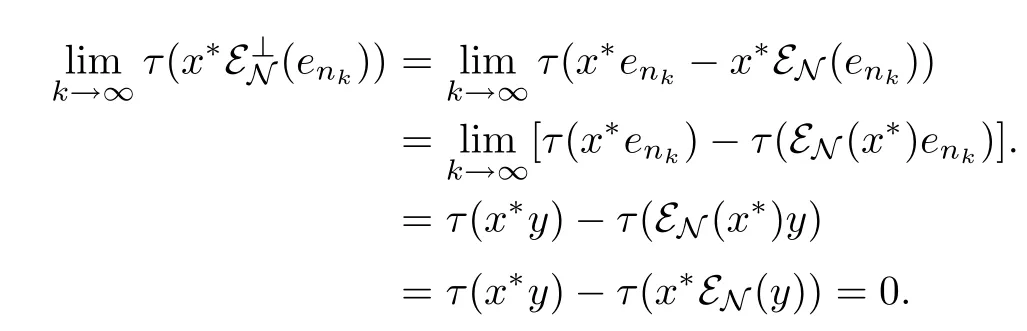
Proof Let x∈M+such that 0≤x≤1.It follows that 0≤εn（x）≤1.For any positive integer N，define

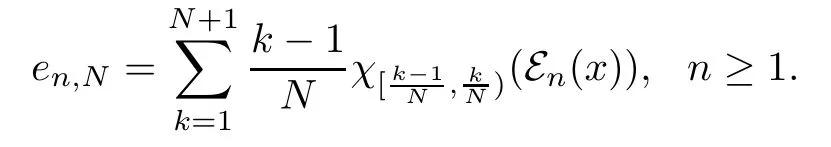
Therefore，

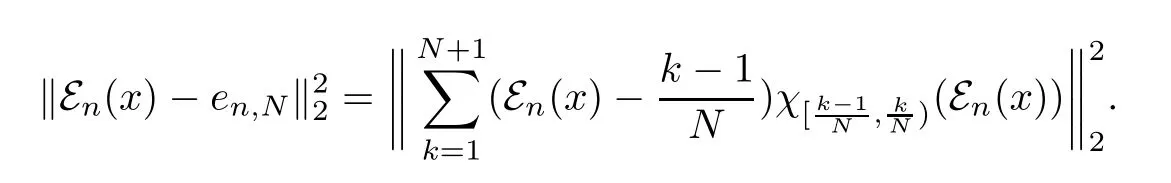
For any 1≤i＜j≤N+1 we have

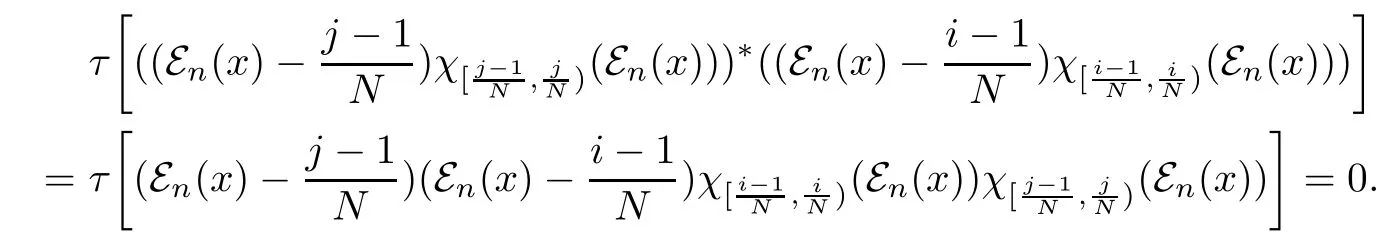
Thus

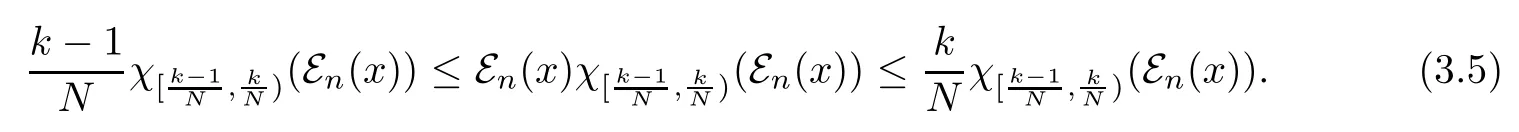
By（3.4）and（3.5），we deduce that

Since en，Nis a linear combination of projections，by hypothesisin L2（M）as n→∞.Therefore，for any y∈L2（M），

Combining（3.6）and（3.7），we deduce that

Since N is arbitrary，we deduce that ε⊥N（εn（x））w-→0 in L2（M）as n→∞.For any x∈M+，by considering~x=‖x‖-1x，we also have ε⊥N（εn（x））w-→0 in L2（M）as n→∞.This result willalso hold for x∈M.To prove this，we only need to decompose x into a sum of four positive operators:x=a+-a-+i（b+-b-）and apply the above result to them.Finally，for x∈L2（M）and ε＞0，there exists x′∈M such that‖x-x′‖2＜ε.For any y∈L2（M）we have that

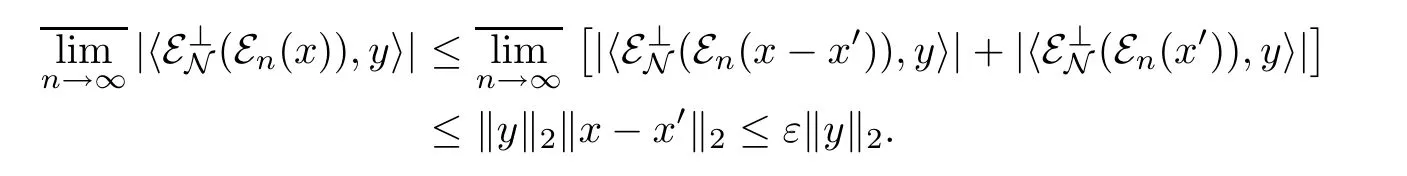
Thus ε⊥N（εn（x））w-→0 in L2（M）as n→∞（x∈L2（M））.The proof is completed. □

Corollary 3.9 If Mn⊥-→N，then εn（x）L2（M）----→0 for any x∈L2（N）⊥.

Proof Let x∈L2（N）⊥.Because ε⊥N（x）=x，we have

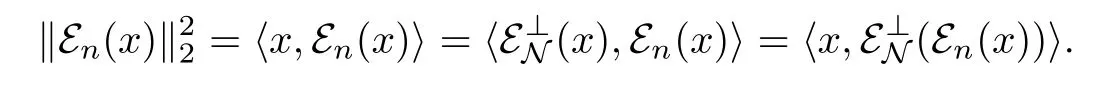
Since Mn

⊥-→N，we have ε⊥N（εn（x））w-→0 by Lemma 3.8.ThereforeWe have proved the corollary.

Proof Let x，y∈L2（M），then

For the first term of（3.8）we have

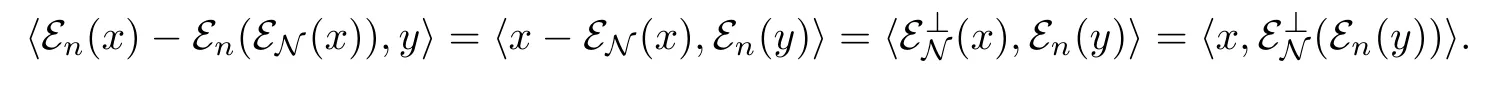
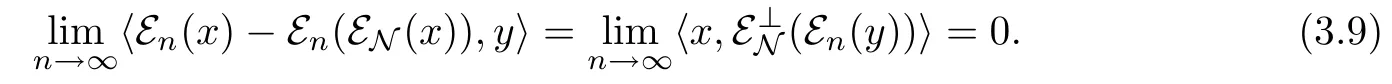
For the second term of（3.8），sincewe haveby

Theorem 3.2.Therefore，

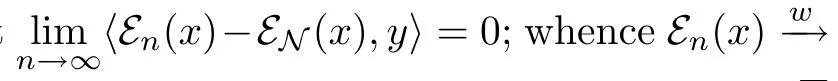
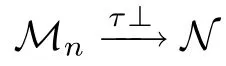
by Lemmas 3.8 and 3.10，we have

so‖εn（x）-εN（x）‖2→0.If 1≤p＜2，since‖εn（x）-εN（x）‖p≤‖εn（x）-εN（x）‖2，we have that‖εn（x）-εN（x）‖p→0.If 2＜p＜∞，we assume first that x∈M，then

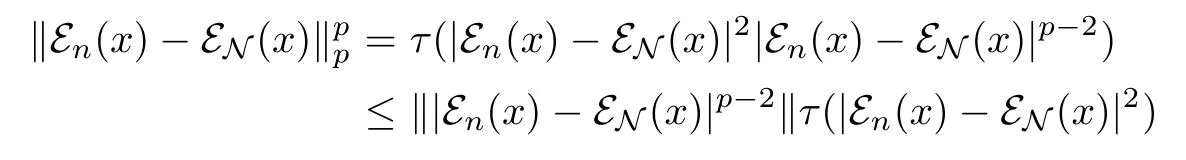
Since M is dense in Lp（M），we deduce that‖εn（x）-εN（x）‖p→0 for any Lp（M）.

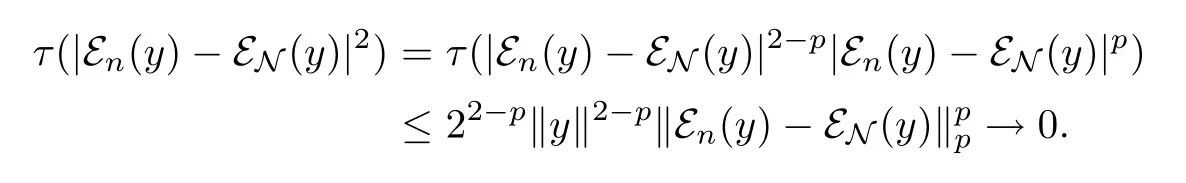
This is also true for y∈L2（M）Since M is dense in L2（M）.

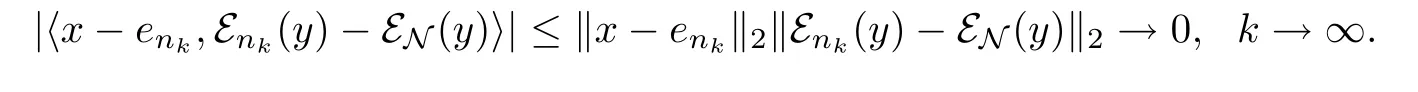
Then

［1］Alonso A.Lp-continuity of conditional expectations.J Math Anal Appl，1998，221:161-176

［2］Alonso A.A counterexample on the continuity of conditional expectations.J Math Anal Appl，1988，129（1）: 1-5

［3］Bekjan T N，Chen Z Q.Interpolation and Φ-moment inequalities of noncommutative martingales.Probab Theory Related Fields，2012，152:179-206

［4］Pisier G，Xu Q.Non-commutative Lp-spaces//Johnson W B，Lindenstrauss J.Handbook of the Geometry of Banach Spaces Vol II:North Holland:Elsevier，2003:1459-1517

［5］Pisier G，Xu Q.Non-commutative martingale inequalities.Comm Math Phys，1997，189:667-698

［6］Segal I E.A non-commutative extension of abstract integration.Ann of Math，1953，57（2）:401-457

［7］Dixmier J.Formes lineaires sur un anneau d′op´erateurs.Bull Soc Math France，1953，81:9-39

［8］Jiao Y.Noncommutative martingale inequalities in symmetric operators spaces.Arch Math，2012，29:1-11

［9］Schatten R.A Theory of Cross-Spaces.Princeton，NJ:Princeton University Press，1950

［10］Dang-Ngoc N.Pointwise convergence of martingales in von Neumnatn algebras.Israel J.Math，1979，34: 273-280

［11］Zhang C，Hou Y L.Convergence of weighted averages of martingales in noncommutative Banach function spaces.Acta Math Sci，2012，32B（2）:735-744

∗Received July，25，2014；revised January 26，2015.This work was supported by National Natural Science Foundation of China（11271293，11471251）and the Research Fund for the Doctoral Program of Higher Education of China（2014201020205）.

†Corresponding author:Congbian MA.