教在儿童学的起点处
——以“三角形的面积计算”教学为例
2015-11-21江苏太仓市实验小学215400查人韵
江苏太仓市实验小学(215400) 查人韵
教在儿童学的起点处
——以“三角形的面积计算”教学为例
江苏太仓市实验小学(215400) 查人韵
教学是有起点的,这个起点不只在教材,更在儿童。随着家庭启蒙教育、学前教育、社会生活等多种因素的影响,儿童的学习起点越来越个性化和多元化,学习起点的研究得到普遍重视。教在学的起点处,就是要从儿童的“现实起点”出发,把儿童的问题、困惑、经验、感受等作为材料,在数学学习活动中实现儿童知识、能力、思维、智慧的生长。
儿童经验 教学起点 三角形面积
“教学起点”、“学的起点”如今已是教师在各级研修活动中的常用词之一。“从学的起点出发”的理念,尊重了学习规律,体现了真正的儿童立场。但是学生学习的起点到底在哪,往往需要教师用心“捕捉”,而不是“想当然”。
曾经听过一节二年级“角的认识”的课。课始,教师让学生看三个坡度不一的滑梯,让学生聊一聊最喜欢玩哪个。学生有的说喜欢玩比较“陡”的,刺激,滑得快;有的说比较喜欢玩“平”一点的,安全、平稳。然后教师让学生思考这三个滑梯里藏着什么数学知识,学生很踊跃地回答,但就是没人提到“角”。最后教师在画面上沿着底面画出一条线,沿着滑梯再画出一条线,由此引出“角”。
这个案例中,滑梯是生活中常见的玩具,儿童大多也有玩的经验,滑梯的坡度跟角度有直接的关联。可是,为什么这个看起来“很生活”“很儿童”“很数学”的东西却没能产生很好的学习效果呢?原因很简单,那就是学生所积累的玩滑梯的经验并不是和“角”联系在一起,更多的是活动中的速度、快感、刺激。加上滑梯本身是个物体,而角是一个平面图形,二者之间的“粘合度”并不是很好,加上教者画出的角的一条边是地面,地面并不是滑梯的一个部分。两个原因叠加,就很容易看出,滑梯未必是学生学习“角”十分恰当的起点。
故而,在教学中,教在儿童学的起点处,不仅很有必要,而且大有文章可做,尤其还要关注不同个体在面对同一学习内容时客观存在的不同起点。下面以“三角形的面积计算”一课为例,谈谈我是如何把握学生的学习起点,引领学生一步步完成学习任务的。
一、尝试探究,找寻起点
课始,让学生自己想办法研究图1中三角形的面积,有困难可以看书。

图1
原以为学生会像课本编排的那样用数格子、转化成平行四边形的方法,可结果大大超乎我的想象,仅有少数人用了数格子、转化成平行四边形的方法,更多的学生想到了长方形(如图2)
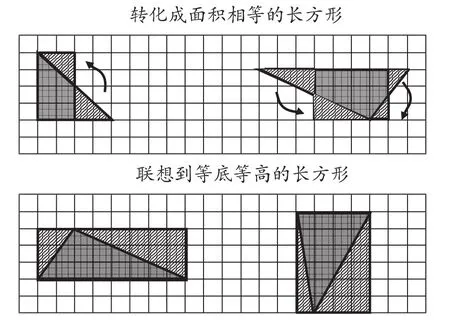
图2
细细想来,出现这样的情况是必然的。首先,数格子最大的麻烦就是有很多地方既不是一整格,也不正好是半格,难以产生精确的数据。此外,从知识的角度看,学生的起点是平行四边形的面积计算,其方法是转化成面积相等的长方形,因此设法转化成面积相等的长方形的确是学生的最近发展区。而从三角形联想到等底等高的长方形,跳出了“等积变形”的局限,具有一定的开拓创新性。
当学生学习的“现实起点”呈现在我面前时,我开始思考:如果从方法的优劣性、普适性的角度,可按数格子、转化成面积相等的长方形、转化成等底等高的长方形、转化成等底等高的平行四边形的顺序,组织学生交流,这样的学习虽能打开学生的研究视野,但恐怕如蜻蜓点水,学生只是表面理解。我又思考:如果每一种方法都很好,为什么教材只介绍转化成等底等高的平行四边形的方法?教师该如何处理好教材与儿童的关系?最终,我决定从儿童的现实起点出发,从多样化走向最优化。
二、基于起点,展开交流
教材的转化为平行四边形的方法是各种方法最优化的结果,也是为后续学习做铺垫的最重要方法。基于大部分学生都没有采用转化成等底等高的平行四边形面积来算,我认为仅仅停留在个别学生的方法介绍层面是不够的,必须要让每个学生亲身经历、积累体验,使体验、方法真正转化成自身的经验。
生1出示图3。
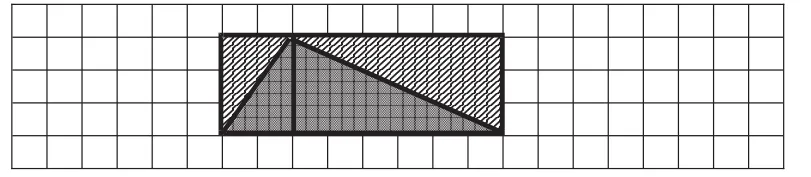
图3
师:能介绍一下你的方法吗?
生1:我是把三角形分成两个小三角形,左边的小三角形面积是长为3厘米、宽为2厘米的长方形面积的一半,3×2÷2=3(平方厘米),右边的小三角形面积是长为6厘米、宽为3厘米的长方形面积的一半,6×3÷2=9(平方厘米),9+3=12(平方厘米)。
生2:我也是这样画图的,可是我和他算得不一样,我是先算出大长方形的面积,然后用大长方形的面积除以2。8×3÷2=12(平方厘米)。
师:看来,计算三角形的面积可以先算算它所在的长方形面积。你能用生3的方法计算下面三角形的面积吗?(出示图4)

图4
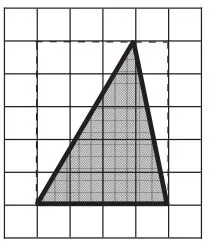
图5
(学生自主尝试转化成等底等高的长方形的方法。为了进一步引导学生掌握这种思路,教师可出示图5。)
师:观察两组图形和算法,你有什么发现?
生3:算三角形的面积,可以先看成长方形来算,然后除以2就行了,4×5÷2=10(平方厘米)。
师:看成怎样的长方形来算?
生4:长和宽相当于三角形的底和高。
师:也就是说,每个三角形都可以看成是一个长方形的一半。
三、想象比较,沟通联系
师(出示图6):请大家大胆想象,这个三角形,还可以看成是什么图形的一半呢?
(学生交流自己的想法后,教师出示图7)

图6

图7
生1:这时的三角形面积是平行四边形的一半。
师:能借助平行四边形面积的计算推算出这个三角形面积吗?
生2:4×5÷2=10(平方厘米)。生3:跟刚才的算式一样呢。
师:比较图5和图7,有什么发现?
生4:三角形的面积都占了一半。生5:长方形面积和平行四边形面积相等,都是用4×5。师:也就是说,把三角形转化成等底等高的平行四边形或长方形,三角形的面积是平行四边形或长方形面积的——一半。
师(再次出示图3):如果将这个三角形也看成是一个平行四边形的一半,这个平行四边形是什么样子呢?你能用两个同样的三角形来演示一下吗?
学生操作演示多种不同的拼法,但是,不管怎么拼,三角形的面积都是平行四边形面积的一半,计算面积也可以用8×3÷2=12(平方厘米)计算。
从学生比较容易理解的方法出发,让学生在讲述和交流中逐步感受到每个三角形都可以看成是它所在的长方形或平行四边形的一半,只要算出长方形或平行四边形面积即可。
让学生独立填写表格。

三角形 与它等底等高的平行四边形底 高 面积 面积4 4 4 5 8 3
我发现:__________________________________。
这一环节,让学生离开直观图形,进入纯运算阶段(也可以结合想象),让学生牢固掌握之前研究出的三角形面积计算的方法(底×高÷2)。
四、科学解释,提升认识
师(出示图8):我发现有的同学也由三角形想到了长方形,但并不是我们刚才研究的方法。这样的转化可以算出三角形面积吗?先看左边的三角形。

生1:左边三角形的面积是4×2=8(平方厘米)。
师:4是三角形的——底,2是三角形的——高的一半。也就是用底乘以——
生2:底ד高÷2”。(板书“底×高÷2”)
师:右边三角形的面积呢?
生3:右边三角形的面积是4×3=8(平方厘米)。
师:如果用底和高来说呢?
生4:高×底÷2。(板书“高×底÷2”)
师:比较“底×高÷2”、“底×高÷2”、“高×底÷2”,有什么发现?
生5:其实是一样的,都是底和高相乘再除以2。
师:是啊,条条大路通罗马,看起来你们研究的方法不一样,但是经过研究,可以发现它们其实是相通的。数学就是这样神奇而有趣。
……
可见,“教在儿童学的起点处”,并不只是说学习的开始,也包括学习的全程。此外,教师的引导,不仅让学生感受到思维的多样化,还能让学生体会到多样性中的统一性和最优性。
(责编 金 铃)
G623.5
A
1007-9068(2015)11-003
