基于组稀疏多核统计学习的财务困境预测

张向荣，胡珑瑛

（1．哈尔滨工业大学 经济与管理学院，哈尔滨150001；2．黑龙江工程学院 经济管理学院，哈尔滨150008）

财务困境是企业所面临的内外部风险因素最终恶化后的综合和显著的表现。一般是指企业因遭受严重的外部挫折或内部财务活动失去控制而使得财务状况所处的危险或紧急状态，一般包括流动性不足、无力支付到期债务、拖欠优先股股利、盈利能力实质性或持续性削弱、甚至破产等情形。财务困境预测是以企业财务信息为基础，对企业在经营管理活动中的潜在财务困境风险进行监测、诊断与报警的一种技术。它贯穿企业经营活动的全过程，以企业的财务报表、经营计划及其他相关的财务材料为依据，利用会计、金融、企业管理、市场营销等理论，采用比率分析、数学模型等方法，发现企业存在的风险，并向利益相关者发出警示，以便采取相应对策的管理方法［1］。

自20世纪60年代以来，财务困境预测在欧美得到广泛发展，从多元判别分析等线性预测模型，到以神经网络模型为代表的各种非参数预测模型，相关的模型、方法层出不穷。在这些模型中，有一个共同的前提假设，就是可以对公司进行分组，其基本的思想即利用企业的各种财务指标，建立判别模型，从而根据企业的总体财务状况进行分类［2］～［8］。

纵观国内外现有的研究成果，财务困境预测方法主要分为两大类：传统统计方法和人工智能专家系统方法。以支持向量机（support vector machine，SVM）为代表的核方法，凭借其良好的非线性数据处理能力，已经在上市公司财务困境预测中得到了足够的重视和广泛的研究。作为机器学习的一个有效方法，SVM能够处理动态的、不稳定数据，具有参数少、保证唯一最优全局解、采用结构风险原则使得模型针对有限样本集合也具有较好的泛化性能等优点。在应用中，特征集和核函数参数的选择对SVM模型的预测性能具有重要的影响。因此，如何选择合适的特征集和核函数参数进一步提高SVM模型的预测性能是研究者关注的焦点。在标准SVM基础上，众多改进形式的SVM分类器被提出来应用于企业财务困境预测。其中一个类型是对SVM自身进行改进，提出了结合模糊理论的支持向量机算法，用于预测企业破产情况。第二类集中在SVM预测模型参数的搜索以及混合模型构建，都在一定程度上进一步提高了SVM的预测性能，如联合利用粒子群算法和人工蚁群克隆算法，对SVM进行参数优化处理，进而提高了财务困境趋势预测的准确性。该研究也代表了当前国内外企业财务困境预测研究的一种重要预测模型类型，即智能优化方法与机器学习、人工智能专家系统模型的结合。第三类则是将特征预处理、特征选择处理同SVM结合，构成相应的混合预测模型；此外，有学者分别将流形学习、偏最小二乘模型等同SVM进行结合，构建了特征提取与预测的联合模型。核方法在财务困境预测中的应用，如线性核与非线性核分类器、核局部Fisher判别分析用于特征提取、利用流形正则化改进SVM，提高了预测精度［6］～［9］。

近年来，多核学习（multiple kernel learning，MKL）理论和方法在分类和预测等应用体现出了相对于单核学习的显著优势。作为有效处理非线性问题的核方法，由单一核函数构成的核机器在学习和应用过程中，很容易遇到样本不平坦分布、数据不规则等实际问题。基于此，有必要将多个核函数进行有效组合，以期望获得更好的处理结果。这些不同的核函数可能是由不同的相似性度量方法得到的，也可能是利用多源数据信息得到的。为了突出这些核函数之间的相似性和差异性，越来越多的多核学习算法得到研究人员的重视与肯定。研究证明，MKL被认为是一项很有前景的技术，在解决实际问题的应用中表现出先进的性能，特别是利用多核来融合多源数据信息。尽管大家都在积极地研究多核，但是传统的多核方法仍然存在严重的局限性。尤其是现有的多核方法通常转化为复杂的优化任务，比较典型的是凸优化问题，例如半定规划，可以用现有的优化技术来解决。尽管凸优化的效果不错，但要解决这样复杂的优化任务往往具有很大的挑战性［10］～［13］。

本文提出了一种稀疏多核学习方法用于财务风险预测。首先，一个利用预定义的基核进行无监督学习。在此过程中，一个稀疏性约束条件被引入，用于限制基核的线性组合，进而改进学习性能和预测模型的可解译性。通过无监督学习可以得到一个“最优”的线性组合核。最终，这个“最优”组合核用于支持向量机中，进而得到具备稀疏学习能力的多核预测机。本文利用214对ST和非ST公司财务数据进行了仿真实验。实验结果证实，本文所提出的稀疏多核学习方法在全部数据集和不同产业数据集上均优于现有的主流预测方法。

一、基于核学习的预测方法

（一）支持向量机到多核学习

支持向量机（Support Vector Machine，SVM）是针对两类问题的判别分类器，给定N个独立同分布的样本｛（xi，yi）｝，xi是D维的输入向量，yi∈｛－1，＋1｝是其对应的类别标签。SVM的目的是在特征空间中寻找拥有最大分类间隔的线性判别准则，其中特征空间是由映射函数Φ：ℝD→ℝS对原始空间数据进行映射得到的。判别函数形式为：

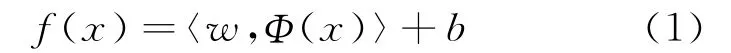
分类器可以通过求解以下二次优化问题来进行训练：

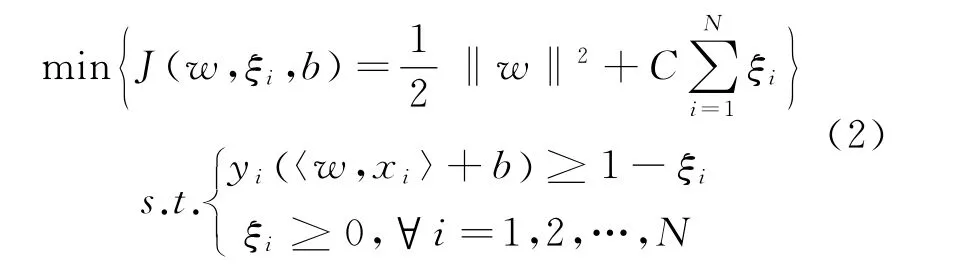
其中w是确定分类超平面的法向量，ξi为松弛变量，对应数据点xi允许偏离函数间隔的量，b为截距，C是惩罚因子，用于控制目标函数中两项之间的权重，实现对学习能力和泛化能力的折衷。

上述问题可通过拉格朗日对偶法变换到对偶变量的优化问题，进而得到一种更加有效的方法来进行求解。这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然地引入核函数。如此，给出原问题的对偶问题：

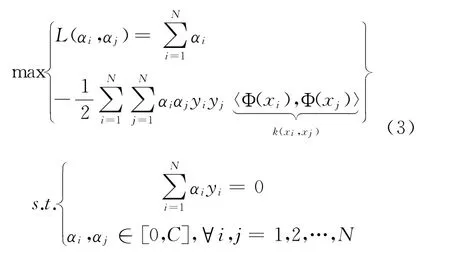
其中，k：ℝD×ℝD→ℝ为核函数（Kernel Function），α为对偶变量。通过求解这个问题，得到和判别函数：

在训练过程中，合理选取核函数k（·，·）及其参数（如q或σ）就显得尤为重要。近些年来提出的多核学习（Multiple kernel learning，MKL）方法替代了选取单一核函数的方法而得到了很大发展，其一般形式为：

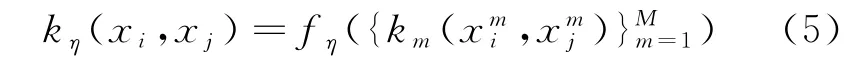
这里，fη：ℝP→ℝ为核函数的组合函数，它可以是线性的或非线性的函数。核函数为｛km：ℝDm×ℝDm→ℝ｝Mm＝1，其可以输入具有M个特征的数据样本xi＝xmi｛ ｝Mm＝1，其中xmi∈ℝDm，Dm为第m个特征的维数。η为组合函数的参数，其更一般的表达式为：

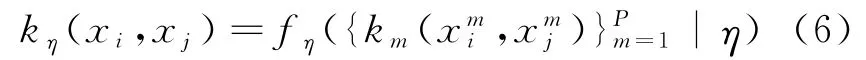
这个参数用于组合预先定义好的核函数（有时也称基核，即训练之前给定的核函数及其参数）。

（二）代表性多核学习方法

多数现有的多核学习方法都是从学习模型的目标函数出发，构造同时求解多核组合和目标极值的最优化问题。将多核特征空间嵌入公式（2）中，可以得到多核SVM的优化问题：

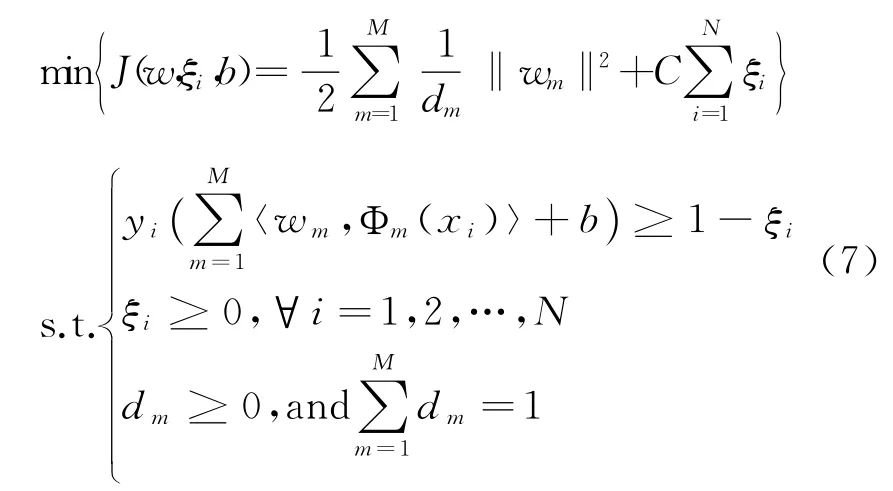
其中wm是第m个希尔伯特特征空间中的决策超平面的权向量，对应核Km的非线性映射函数为Φm（xi）。

多核SVM的对偶优化问题表示为：

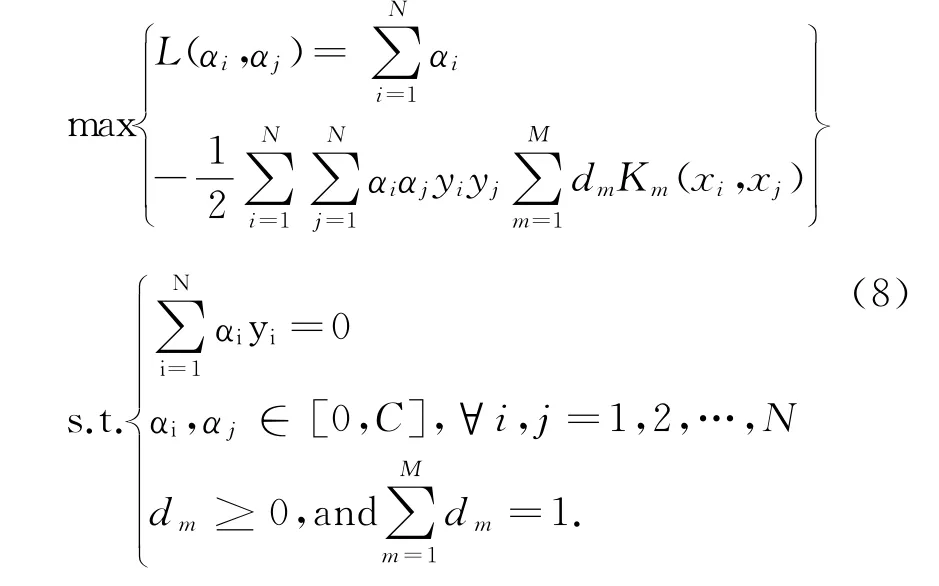
公式（3）中的目标函数L（αi，αj）是一个外凸且可微的函数，因此多核组合系数dm可以通过迭代更新L（αi，αj）的梯度下降方向求得最优解。在主流的多核学习算法中，SimpleMKL即利用梯度下降法迭代优化多核SVM决策函数。

目标函数的梯度表示如下：

沿着梯度下降的方向D更新组合系数：

其中γ是迭代更新步长，d＝［d1，d2，…，dM］T是多核组合系数向量。并不需要在每次迭代中都计算新的梯度，只有当目标函数的值下降时才需要更新梯度。梯度迭代更新的过程直到满足终止条件为止。终止条件可以根据对偶区间、KKT条件或者d的变化等。

二、组稀疏多核学习方法

（一）多核Boosting学习的基本形式基于对数组选择的稀疏多核学习

正如上一节所述，在进行多核学习之前，候选基核函数已经确定。一般的多核学习过程中会赋予每个基核函数一定的权值，以寻求最优的基核线性组合。不同于一般的多核学习，稀疏多核学习目的在于学习具有少量非零权值的组合核。通过这样的处理，去除在学习过程中存在冗余的基核，最终得到的权值在一定程度上代表了该基核学习能力的重要性。

上面公式（7）给出了多核学习的一般形式。由该公式我们可以看出，最大化边缘意味着来自不同Hilbert空间的基核构成一个加权距离形式。不同的基核之间存在一定的相关性，因此，借助于文献［13］提出的方法，我们引入组选择项（Group Selection Term，GST）来描述这种关系。通过引入对数组选择项到多核学习的线性组合中，稀疏多核学习问题可以表示为如下形式：

其中g（w）给出了罚函数项。

文献［13］给出了三种罚函数的具体形式。这样，方程（11）可以重新描述为如下形式：

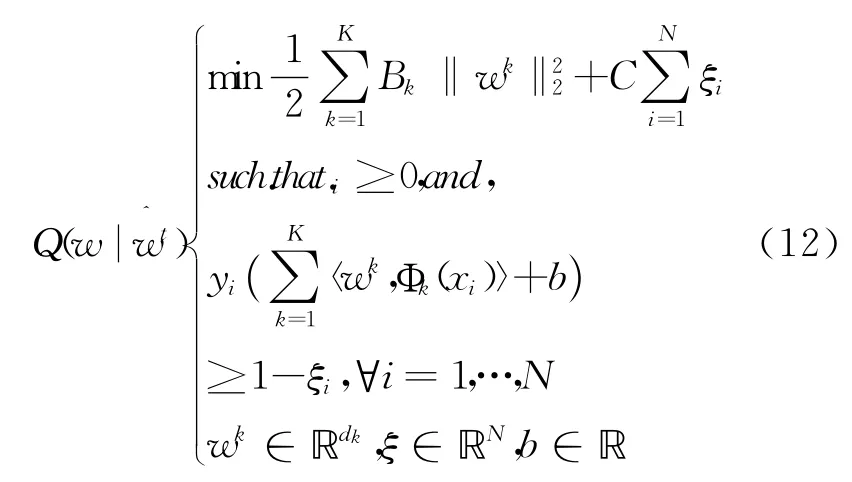
其中Bk是罚函数g（w）的上界。

进一步，方程（7）的对偶优化问题可以描述为：

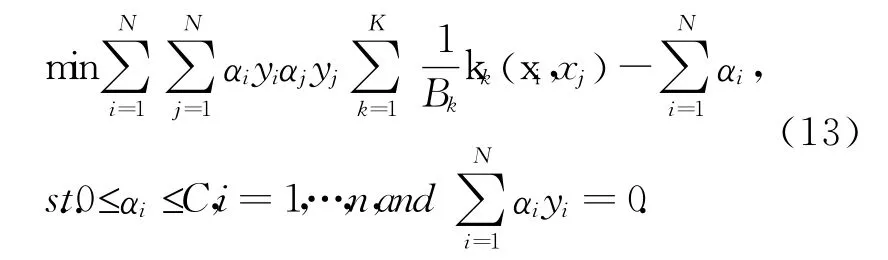
由此可见，上述形式具有同单核标准支持向量机一致的优化问题形势，只是引入了k另Ω为一个对角矩阵，有Ωjj＝Bk，j∈sk。方程（13）拉格朗日函数形式：

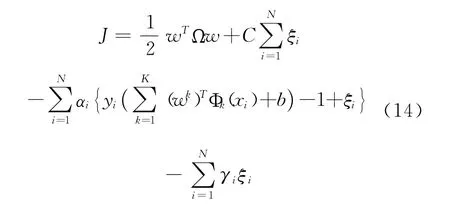
上述方程可利用标准支持向量机来进行求解，具体求解方法可见文献［12］。

（二）组稀疏多核学习财务预警过程

利用组稀疏多核学习进行财务预警的主要步骤可以描述如下：

（1）采集中国上市公司财务比率指标，并对其进行归一化；

（2）确定训练数据和测试数据集；

（3）确定基核形式和基核数目；

（4）利用组稀疏多核学习进行训练数据的学习，并计算得到稀疏多核中基核函数的权值，进而得到组稀疏多核学习预测模型；

（5）在测试数据集上，进行预测处理。

三、仿真实验

（一）数据描述

为了测试所提出方法用于财务困境预测的有效性，本文由中国上市公司中选择实际财务数据指标进行研究。财务数据采集原则主要考虑了公司的多样性、时间的连续性和每类样本的比例。实验选择了207家财务状况正常的公司和207家ST公司，财务指标周期涵盖了2006年至2012年。根据上述准则，44个不同的原始财务指标数据选用实验中。相关的实验数据见表1。

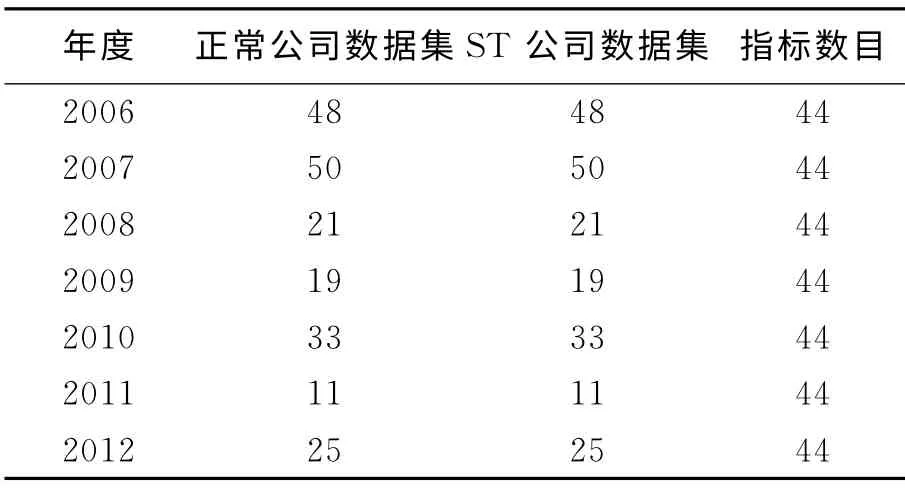
表1 实验数据

（二）实验结果

为了验证所提出方法的有效性和先进性，在仿真实验中本文选用了当前典型的财务困境预测方法作为对比。对于不同的方法，每组实验中选择相同的训练集和测试集。第一组实验主要用于测试不同预测方法的预测精度。这组实验数据包括全部年限数据预测精度和不同行业预测精度。对比的方法包括：经典的多线性分析MDA、Logit方法、k近邻（KNN）、神经网络NN和标准支持向量机。第二组实验主要用于测试不同方法进行财务指标特征提取的能力，即提取的特征用于最终预测的性能。选择对比方法包括：主成分分析＋支持向量机、线性判别分析＋支持向量机、ZETA＋支持向量机方法。

表2给出了六种不同方法的平均预测精度，这里选择了100个公司数据作为训练样本，时间模型为T－1、T－2和T－3。由表2可以看出，本文所提出的方法在平均预测精度方面，明显优于其他常用方法。进一步，为了评价不同方法在训练样本数目变化情况下的预测能力，我们在实验中改变训练样本数目，由10到100变化，间隔为10，并采用T－2模型。表3给出了预测精度测试结果。进一步，我们在实验中测试了不同方法用于不同行业公司财务困境预测能力。相应的行业数据预测结果列于表4中。其中，C1表示能源行业或矿业公司，C2表示电子工业公司，C3表示地产行业公司。由表4列出的实验结果可以看出，本文所提出的方法在不同行业数据中，大多数情况都要优于其他常用预测方法。

表2 全部数据集测试的预测精度（训练样本数为100）

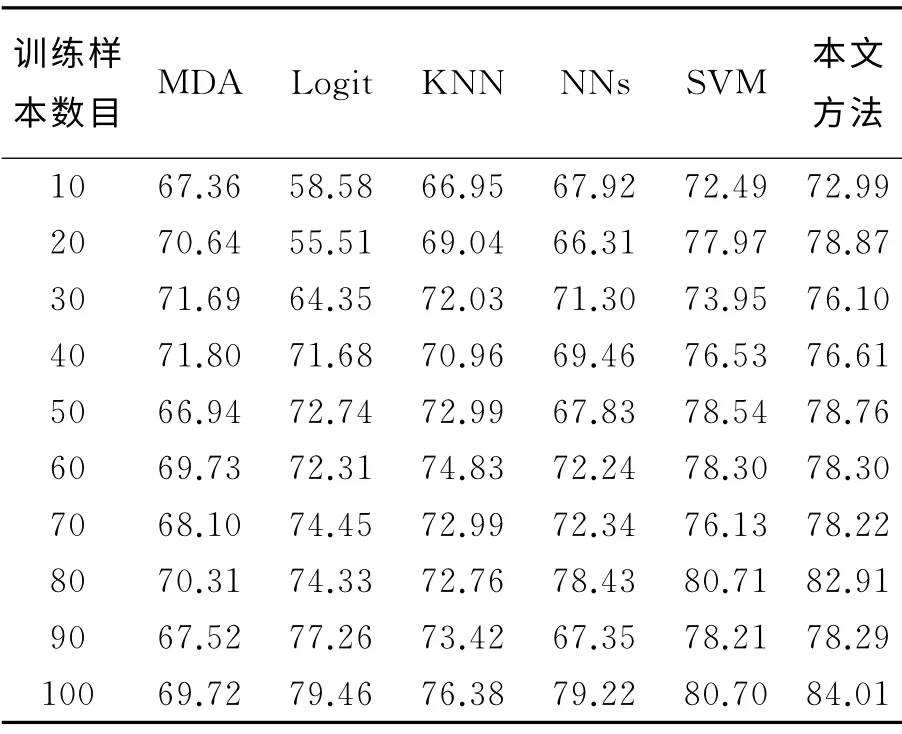
表3 T－2模式不同训练样本数目下预测精度

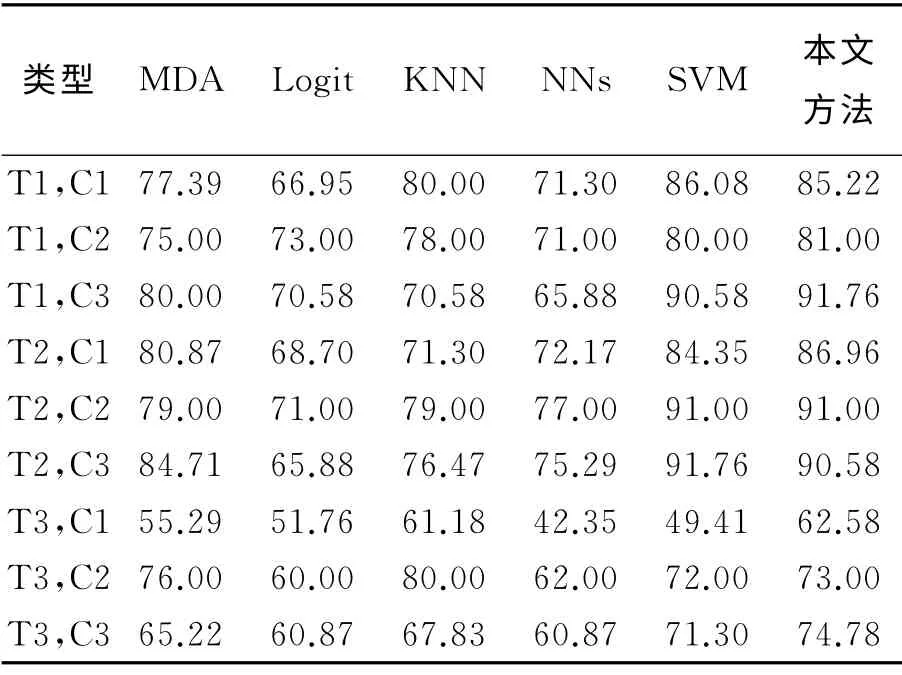
表4 三类不同行业预测结果

本文所提出的方法由于具备组稀疏特性，因此能够在预测的同时实现特征的选择，即财务指标的选择。换言之，通过将不同指标指定给不同的基核，在学习过程中通过控制基核权值的非零数目，会选择性地自动保留对于预测更为有效的指标，进而实现指标的自动筛选过程。表5给出了在进行特征选择下的预测精度实验结果。

表5 全部数据集测试的特征提取后预测精度（训练样本数为100）

结 论

针对上市公司财务困境预警问题，本文提出了一种基于组选择的稀疏多核学习方法。该方法的主要特点在于通过引入对数组选择项作为罚函数，达到去除大量基核之间预测能力冗余的目的，通过去除冗余的基核函数，实现更优性能的财务困境企业预测能力，与此同时对用于财务困境预测的企业财务数据指标具备良好的选择性能。利用中国上市公司真实数据进行的仿真实验结果表明，同现有预警方法相比，本文提出的方法能够取得良好的预测结果。

［1］BEAVER W．Financial Ratios as Predictors of Failure［J］．Journal of Accounting Research，1966，4：71–111．

［2］ALTMAN E I．Financial Ratios Discriminant Analysis and the Prediction of Corporate Bankruptcy［J］．Journal of Finance，1968，23：589－609．

［3］OHLSON J A．Financial Ratios and the Probabilistic Prediction of Bankruptcy［J］．Journal of Accounting Research，1980，18（1）：109－131．

［4］CARLOS S C．Self－organizing Neural Networks for Financial Diagnosis［J］．Decision Support Systems，1996，17：227－238．

［5］CHO S，KIM J，BAE J K．An Integrative Model with Subject Weight Based on Neural Network Learning for Bankruptcy Prediction［J］．Expert Systems with Applications，2009，36：403－410．

［6］CORTES C，VAPNIK V．Support－Vector Networks［M］．Machine Learning，1995，20：273－297．

［7］CHEN L H，HSIAO H D．Feature Selection to Diagnose a Business Crisis by Using a Real GA－based Support Vector Machine：An Empirical Study［J］．Expert Systems with Applications，2008，35：1145－1155．

［8］DING Y，SONG X，ZEN Y．Forecasting Financial Condition of Chinese Listed Companies Based on Support Vector Machine［J］．Expert Systems with Applications，2008，34：3081－3089．

［9］FRIENDMAN J H，HALL P．On Bagging and Nonlinear Estimation［J］．Journal of Statistical Planning and Inference，2007，137：669－683．

［10］GOENEN M，ALPAYDN E．Multiple Kernel Learning Algorithms［J］．Journal of Machine Learning Research，2011，12：2211－2268．

［11］RAKOTOMAMONJY A，et al．SimpleMKL［J］．Journal of Machine Learning Research，2008，9：2491－2521．

［12］SUBRAHMANYA N，SHIN Y C．Sparse Multiple Kernel Learning for Signal Pprocessing Applications［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（5）：788－798．

［13］BACH F R，et al．Multiple Kernel Learning，Conic Duality，and the SMO Algorithm［C］／／Proc．21st Int’l Conference on Machine Learning．2004：41－48．