线性规划在生产计划制定中的应用

陈利群

线性规划在生产计划制定中的应用

陈利群

确定合理的生产计划是企业生产管理的重要问题，关系到企业的生存和发展。文章利用数学模型解决万头猪场的计划制定问题。利用具体实例展示如何有效地将现实的生产计划问题转化为数学模型，然后定量地给出科学决策，体现线性规划解决实际问题的简捷性和方便性。

线性规划；计划制定；数学模型

在现代工农业生产、交通运输以及经营管理工作中，经常遇到在人力、物力、运输力等各种资源一定的前提下，如何调配才能获得最大经济效益的问题。线性规划是运筹学的一个重要分支，专门研究某个整体指标最优的问题，是进行科学管理的一种方法。

确定合理的生产计划是企业生产管理的重要问题，关系到企业的生存和发展。对大多数企业来说，都需要定量的而非定性的给出生产计划，数学在这个过程中发挥着举足轻重的地位。数学领域中线性规划这一分支的解法，到目前为止已经发展得比较完善，而且大多数企业的生产管理问题都可以转化为线性规划，所以在实际生产计划中线性规划的有效利用将会对企业的生产管理起到至关重要的作用。

一、线性规划数学模型

生产计划是一种典型的复杂系统，利用模型描述这类系统是一件非常困难的工作，为此建模和求解过程中对研究对象做出一些简化是非常必要的。甚至可以说，在如何求解的问题上可以不做要求，而最重要的是要善于针对本企业面临的内外具体实际情况，建立起实用的模型，并能从这些模型的模拟结果中，找出企业生产经营中存在问题的症结所在，从而制定出符合实际的高效益的企业生产战略和策略。由于生产计划问题分析完全符合线性规划建模的条件，因此可以运用线性规划来分析生产计划方案优化问题。

用线性规划解决生产计划问题的关键在于如何将实际问题进行简化、处理转化为数学问题，以及如何选取合适的变量。下文将通过具体实例展示如何将现实的生产计划问题转化为数学问题，对数学问题进行求解，最终用科学的方法指导实际的生产操作。

二、案例背景及相关数据

养猪业是关系国计民生的重要产业，它直接影响到社会稳定、经济发展的全局。猪肉是我国大多数城乡居民的主要副食品。我国既是养猪大国，也是猪肉的消费大国，生猪饲养量和猪肉消费量均占世界总量的一半左右。养猪业作为畜牧业中的一部分也是最早步入市场经济的一个产业，近十年来发生了翻天覆地的变化。尤其是近年来各级政府和业务部门纷纷把畜牧业产业结构调整作为农业产业结构的制高点和突破点，出台优惠政策，采取得力措施，使畜牧业摆脱了长期以来对农业的依附地位，转而成为发展农村经济的重要力量。

某养猪场最多能养10000头猪，该养猪场利用自己的种猪进行繁育。养猪的一般过程是：母猪配种后怀孕约114天产下乳猪，经过哺乳期后乳猪成为小猪。小猪的一部分将被选为种猪（其中公猪母猪的比例因配种方式而异），长大以后承担养猪场的繁殖任务；有时也会将一部分小猪作为猪苗出售以控制养殖规模；而大部分小猪经阉割后养成肉猪出栏，见图1。

1.假设生猪养殖成本及生猪价格保持不变，且不出售猪苗，小猪全部转为种猪与肉猪，要达到或超过盈亏平衡点，每头母猪每年平均产仔量要达到多少？

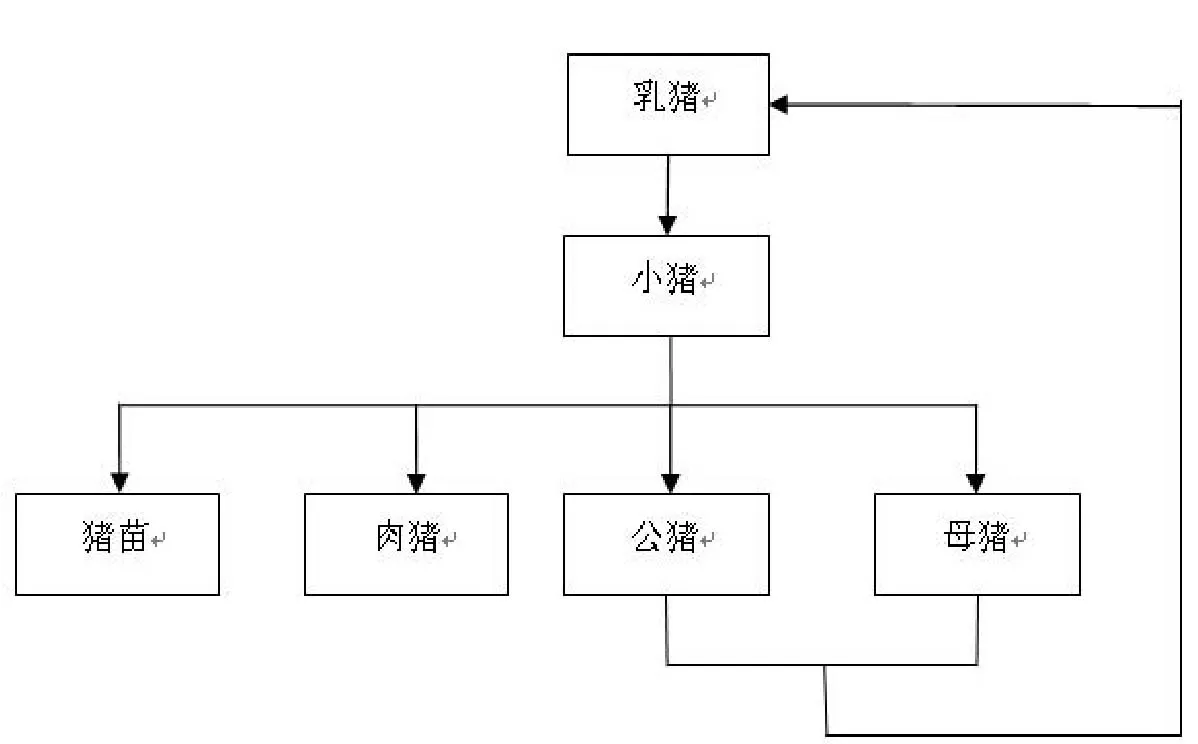
图1

2.生育期母猪每头年产2胎左右，每胎成活9头左右。求使得该养殖场养殖规模达到饱和时，小猪选为种猪的比例和母猪的存栏数，并结合所收集到的数据给出具体的结果。

三、相关假设及相关说明

（一）基本假设

公猪与母猪的比例为1∶25；

不考虑外部因素（包括天灾、疾病等情况下），猪的成长周期不变；

小猪的存活率为90%、哺乳仔猪成活率为90%、断奶仔猪成活率为95%，以及生长育肥成活率为98%；

种猪的年更新率为1/3；

养殖场养殖规模达到饱和为10000头猪；

在计算猪场成本时，假定猪场的各项固定成本都已分摊到每头猪的成本上。

（二）符号说明

P0：母猪的基数

I1：每头公猪的成本

I2：每头母猪的成本

I3：每头肉猪的成本

（三）猪场猪群结构说明

1.成年母猪数：P0

2.后备母猪数：

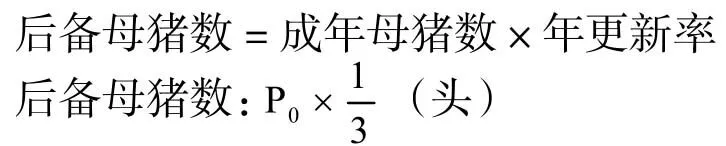
3.成年公猪数：

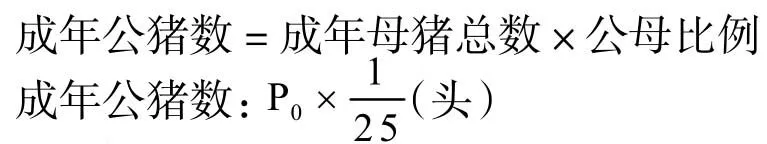
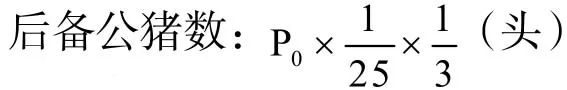
4.后备公猪数：5.哺乳仔猪头数：

哺乳仔猪头数：

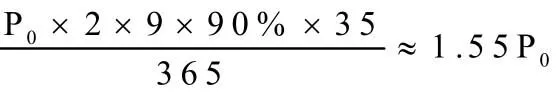
6.保育仔猪数：

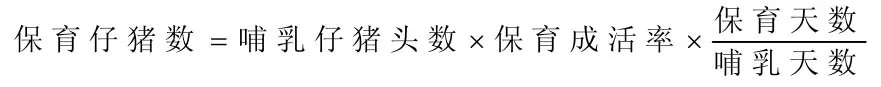
7.生长育肥猪数：

四、模型建立及求解

（一）问题一

1.问题分析

假设猪肉的价格变化趋势在短时间内只与时间有关系，在不考虑国家宏观调控和猪饲料价格变动以及疾病等其他因素的情况下，假设小猪的存活率为90%、哺乳仔猪成活率为90%、断奶仔猪成活率为95%、以及生长育肥成活率为98%，并结合以上几个假设，用代数式表示出公猪的基数、母猪的基数、公猪的成本、母猪的成本、肉猪的成本、肉猪的价格。

根据题意，如不出售猪苗，则猪场收入主要来源于出售的肉猪；另一方面，猪场的成本则主要来自公猪、母猪和肉猪的成本，肉猪包括哺乳仔猪、保育仔猪和生长仔猪。如果在生猪养殖成本及生猪价格保持不变，且不出售猪苗，小猪全部转化为种猪与肉猪的情况下，要达到或超过盈亏平衡点，那么猪场的收入至少必须等于猪场的成本。

2.建立模型

建立收支平衡方程，即

新增的肉猪数×肉猪价格=公猪的成本+母猪的成本+肉猪的成本

另一方面，结合生猪头数数量关系，有

母猪数×母猪平均年产仔量×小猪的存活率×哺乳仔猪成活率×断奶仔猪成活率=新增肉猪数+新增母猪数+新增公猪数

3.模型求解

设新增肉猪数为X0，肉猪价格为M0，每头公猪的饲养成本为I1，每头母猪的饲养成本为I2，肉猪的饲养成本为I3，每头母猪年平均产仔量，则有

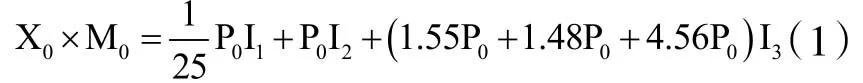
结合查阅到的统计资料，带入小猪的存活率、哺乳仔猪成活率和断奶仔猪成活率，得

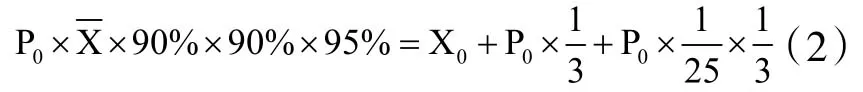
其中，M0、I1、I2、I3可参照当前市场价格视为已知参数，联立（2）、（3），容易求解

则每头母猪年平均产仔量为：

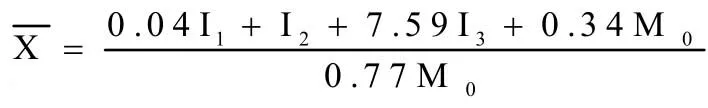
（二）问题二

1.问题分析

假定猪场猪结构呈稳定状态，结合假设用代数式分别表示出猪场中各类猪的数量，即成年母猪数、后备母猪数、成年公猪数、后备公猪数、哺乳仔猪数、保育仔猪数和生长育肥猪数。生育期母猪每头年产2胎左右，每胎成活9头左右，如果该养殖场规模达到饱和，则猪场猪总头数应该达到10000头，利用猪场猪头数便可得出数量关系式。

2.数学建模

猪场猪总头数=成年母猪数+后备母猪数+成年公猪数+后备公猪数+哺乳仔猪数+保育仔猪数+生长育肥猪数

3.模型求解

小猪选为种猪的比例：

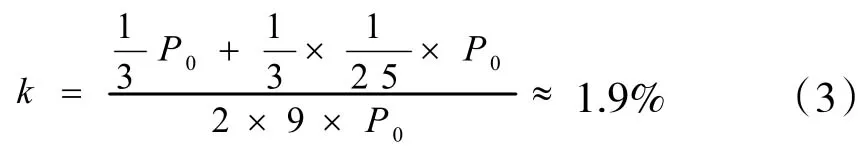
猪场猪的数量关系：

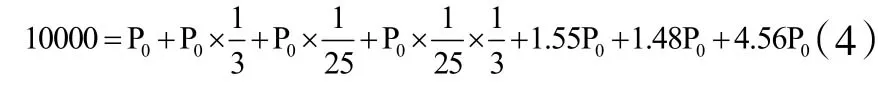
求解（4）式，则母猪的存栏头数

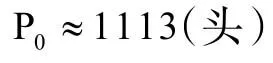
五、总结

随着改革开放和我国经济的高速发展，产业结构调整加快步伐，养殖业也在不断发展，传统的养殖业，逐渐地走向规模化、集团化、一体化和现代化。规模化养猪逐渐占据主导地位后，中国养猪业生猪市场必然会趋于长期的合理盈利的相对稳定，且规模化养猪有利于控制疫病及生产水平的提高，故研究规模化猪场的计划安排问题非常必要。

本文利用猪场的计划安排问题展示如何有效地将现实的生产计划问题转化为数学模型，然后定量地给出科学决策，体现了线性规划解决实际问题的简捷性和方便性。用线性规划解决生产计划问题的关键在于如何将实际问题进行简化、处理转化为数学问题，以及如何选取合适的变量，对数学问题进行求解，最终用科学的方法指导实际的生产操作。今后要继续研究的是如何快速地将实际问题进行简化，建立数学模型，并且能够将所建立的数学模型进行推广，解决相关领域的一系列问题，为企业的生产管理提供科学的依据。

［1］胡运权.运筹学基础及应用［M］.北京：清华大学出版社，2004.

［2］赵书广.中国养猪大成［M］.北京：中国农业出版社，2013.

陈利群，广东创新科技职业学院讲师，硕士，研究方向：模糊数学规划，广东东莞，523960

C934

A

1007-7723（2015）02-0020-0003