局部和稀疏保持无监督特征选择法

简彩仁，陈晓云

（福州大学 数学与计算机科学学院，福建 福州350116）

数据维数灾难普遍存在于模式识别的许多应用中.高维数据集不仅限制传统模式识别方法的应用，还会显著地增加内存和时间开销.特征选择是解决这些问题的有效手段之一［1］.特征选择旨在选择一些相关的特征代表原始的高维数据，而剔除一些不相关的特征.基于聚类的特征选择法［2］，利用聚类算法将数据聚类，用得到的类别信息指导特征选择.然而，由此获得的判别信息是不可靠的.近年来，随着流形学习的兴起，学者提出了新的无监督特征选择方法，如拉普拉斯得分［3］、多簇特征选择方法［4］等.利用L2，1范数的组稀疏性，学者提出了许多嵌入型的特征选择方法，如稀疏限制的无监督最大化边缘的特征选择法［5］、局部和相似保持嵌入特征选择法［6］.这些方法应用在高维小样本数据时，需要求解大规模的特征值问题，不利于问题的求解.而联合特征选择和子空间学习法［7］、联合局部保持投影和L2，1范数构造的特征选择，可以克服大规模特征值的问题.本文提出一种基于局部保持投影和稀疏保持投影的无监督特征选择方法，并利用L2，1范数的组稀疏性质，通过正则化L2，1范数来选择特征.

1 相关工作

局部和稀疏保持无监督特征选择法利用局部保持投影和稀疏保持投影来刻画数据的本质结构.

1.1 局部保持投影

给定数据集X∈Rm×n，局部保持投影（LPP）［8］的目标函数定义为

式（1）中：yi＝VTxi；W＝Wi，j为相似矩阵.

最小化目标函数可以使降维后的样本保持原空间的距离.常见的相似矩阵定义是热核函数.经过简单的代数运算，LPP求解如下优化问题，即

式（2）中：V为投影矩阵；D为对角矩阵，为图拉普拉斯矩阵，L＝D－W.

1.2 稀疏保持投影

稀疏保持投影（SPP）［9］用样本稀疏重构每一个样本xi∈X，得到求解稀疏表示系数的模型为

式（3）中：‖·‖1为1－范数；si＝［si，1，…，si，n］，si，j反映了xi和xj之间的关系.因此，将S＝（si，j）n×n视为仿射权矩阵是合理的.SPP旨在寻找保持稀疏关系的投影，SPP的目标函数为

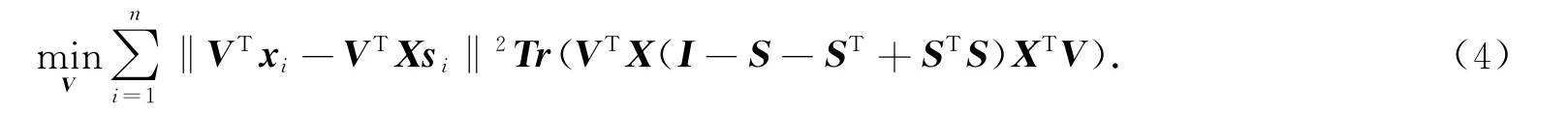
式（4）中：V为投影矩阵.为避免平凡解，通常引入正交约束VTXXTV，V可以通过求解广义特征值问题X（I－S－ST＋STS）XTv＝λXXTv得到.

2 局部和稀疏保持投影特征选择

2.1 目标函数

将式（2）的局部保持项和式（4）的稀疏保持项相结合，得到目标函数为

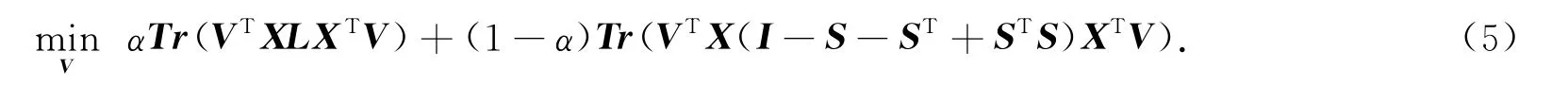
引入L2，1范数来选择有利于保持局部性和稀疏性的相关特征，且为避免平凡解，引入正交约束VTXXTV，得到局部和稀疏保持投影特征选择模型，即

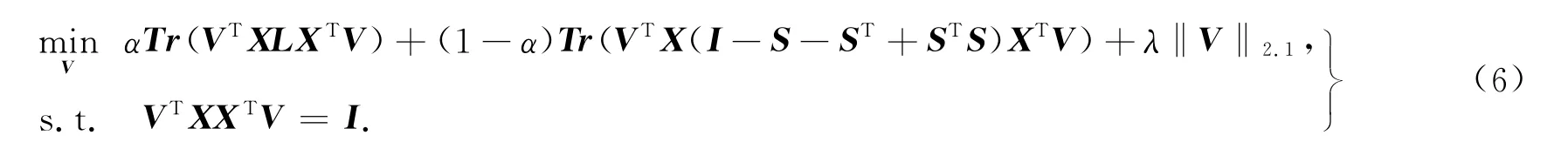
式（6）中：α为平衡参数，用于平衡局部性和稀疏性；λ为正则参数；‖V‖2.1定义为

当获得投影矩阵V后，可以利用vi的2范数，即‖vi‖2来选择特征，其值越大表示该特征越重要.

2.2 模型求解

式（6）可以写为

式（7）中：A＝αL＋（1－α）（I－S－ST＋STS）.式（7）可以利用广义特征值问题求解.但是，当X是高维小样本数据时，式（7）需要求解大规模的特征值问题，且会造成矩阵不可逆的问题.

类似于文献［7］，采用分步求解的方法避免上述困难.令Y＝XTV，有

式（8）的解为Y＊＝［y1，…，yd］，其为A的最小d个特征值对应的特征向量.求解如下的问题得到式（7）的解，即

该问题可用拉格朗日乘子法迭代求解［7］.拉格朗日函数为

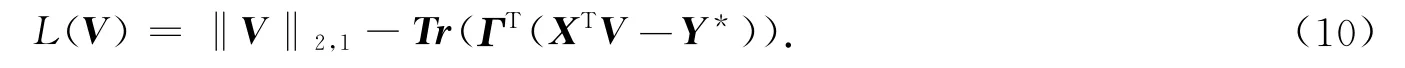
对V求导得

式（11）中：Di，i＝1／（2‖vi‖2），vi≠0，当Di，i＝0时，用一个较小的正数替代，确保D可逆［8］.不难求得

将式（12）代入式（11），可得

由式（12），（13）交替迭代直至收敛，可得投影矩阵V.通过上述讨论可以得到局部和稀疏保持投影无监督特征选择法（LSP）.Input：数据矩阵X；Output：特征子集.1）计算拉普拉斯矩阵L和稀疏表示矩阵S；2）通过式（8）计算最小d个广义特征值对应的特征向量Y＊；3）求解式（9）得到投影矩阵V；4）将‖vi‖2降序排列，选取前p个特征构成特征子集.

3 实验分析

相似矩阵通过W＝（|S|＋|ST|）／2计算.其中：S为稀疏矩阵，可以避免近邻数量的选择；平衡参数α＝0.8.选用数据方差（DV）、拉普拉斯得分（LS）［3］、多簇特征选择方法（MCFS）［4］、联合特征选择和子空间学习法（JFSSL）［7］作为对比方法.LS，MCFS和JFSSL的近邻数量取5，MCFS，JFSSL和LSP的降维维数d取类别个数.通过对选取的特征子集进行聚类分析，对比聚类准确率（ACC）来验证特征选择的有效性.实验环境为Windows 7系统，内存为2G，用Matlab 2010b编程实现.

对给定样本，令ri和si分别为聚类算法得到的类标签和样本自带的类标签，则聚类准确率［10］为

式（14）中：n为样本总数；δ（x，y）为函，当x＝y时，其值为1，否则，为0；map（ri）为正交函数，将每一个类标签ri映射成与样本自带的类标签等价的类标签.

3.1 数据集

选用6个公开数据集进行实验，如表1 所示.表1 中：DLBCL，LUNGCANCER，LEUKEMIA，TOX 为基因表达数据集；ORL，PIE为图像数据集.

3.2 实验结果与分析

应用每种方法选取特征子集，选取的特征个数依次设为｛5，10，15，…，95，100｝，采用K－means对选取的特征子集进行聚类分析，运行20次.各种方法的平均聚类准确率，如表2所示.聚类准确率与特征数量（n）的关系，如图1所示.

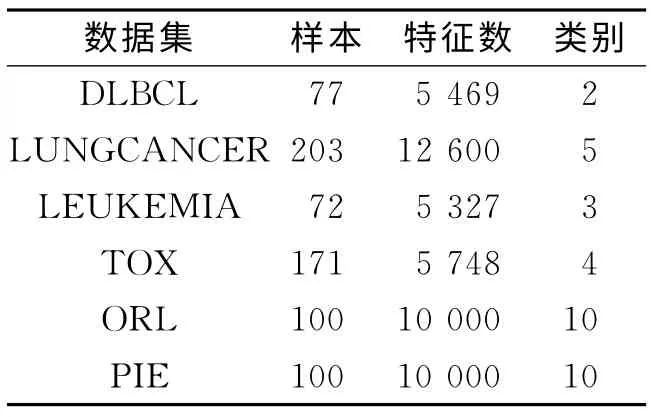
表1 数据集描述Tab.1 Summary of data sets

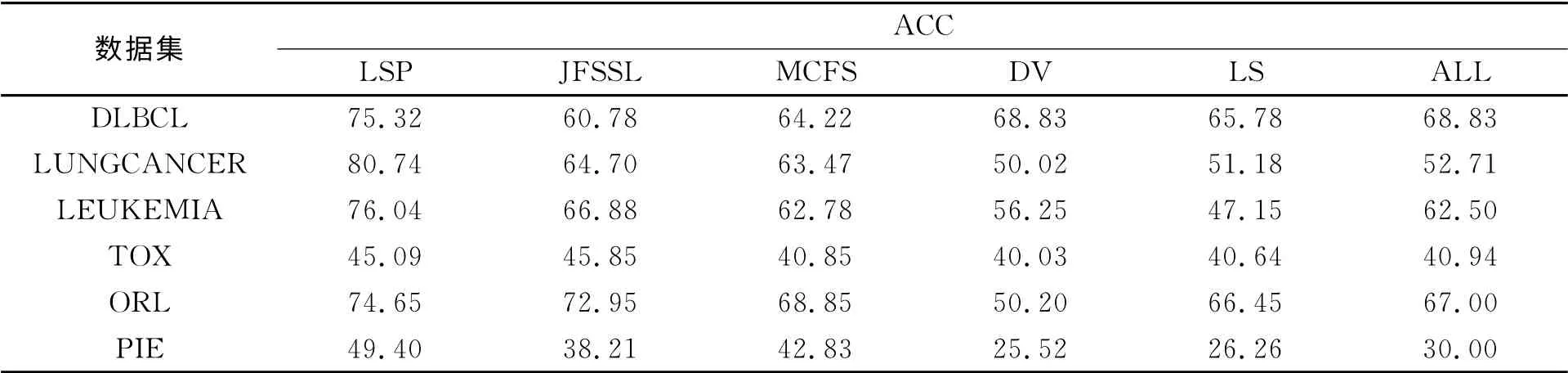
表2 平均聚类准确率Tab.2 Average clustering accuracy %

由表2，图1可知：局部和稀疏保持投影无监督特征选择法具有良好的特征选择能力，除TOX 数据集外，其聚类准确率的平均值最高.与MCFS和JFSSL相比，LSP的聚类效果更为理想，这说明稀疏保持性质也可以刻画数据的本质结构.与DV 和LS相比，因为DV 和LS只考虑独立的计算每个特征的得分，而忽略了特征之间的相互作用，所以考虑特征之间的关系可以提高聚类准确率.此外，用LSP进行特征选择与保留全部特征（ALL）可以明显地提高聚类的准确率.因此，利用局部和稀疏保持投影构造的无监督特征选择法是有效的.

3.3 参数讨论

平衡参数α在｛0，0.1，0.2，…，0.9，1.0｝变化时，平均聚类准确率的情况，如图2所示.由图2可知：总体上，平衡参数α对LSP的影响是明显的；当α为0.6～0.9时，LSP 的聚类准确率在较高的水平上保持相对稳定.在这一范围内稀疏保持项的比重较大，说明稀疏保持项可以提高特征选择的能力.

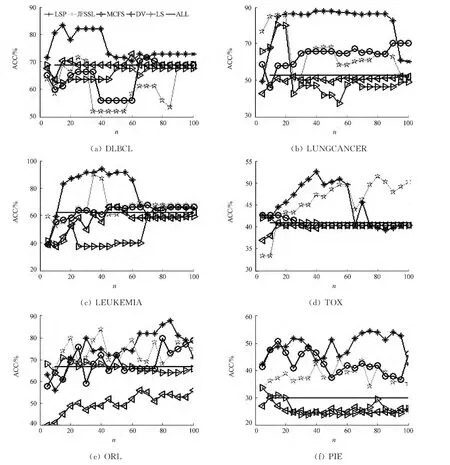
图1 聚类准确率与选择的特征数量关系Fig.1 Relation between clustering accuracy and the number of selected features

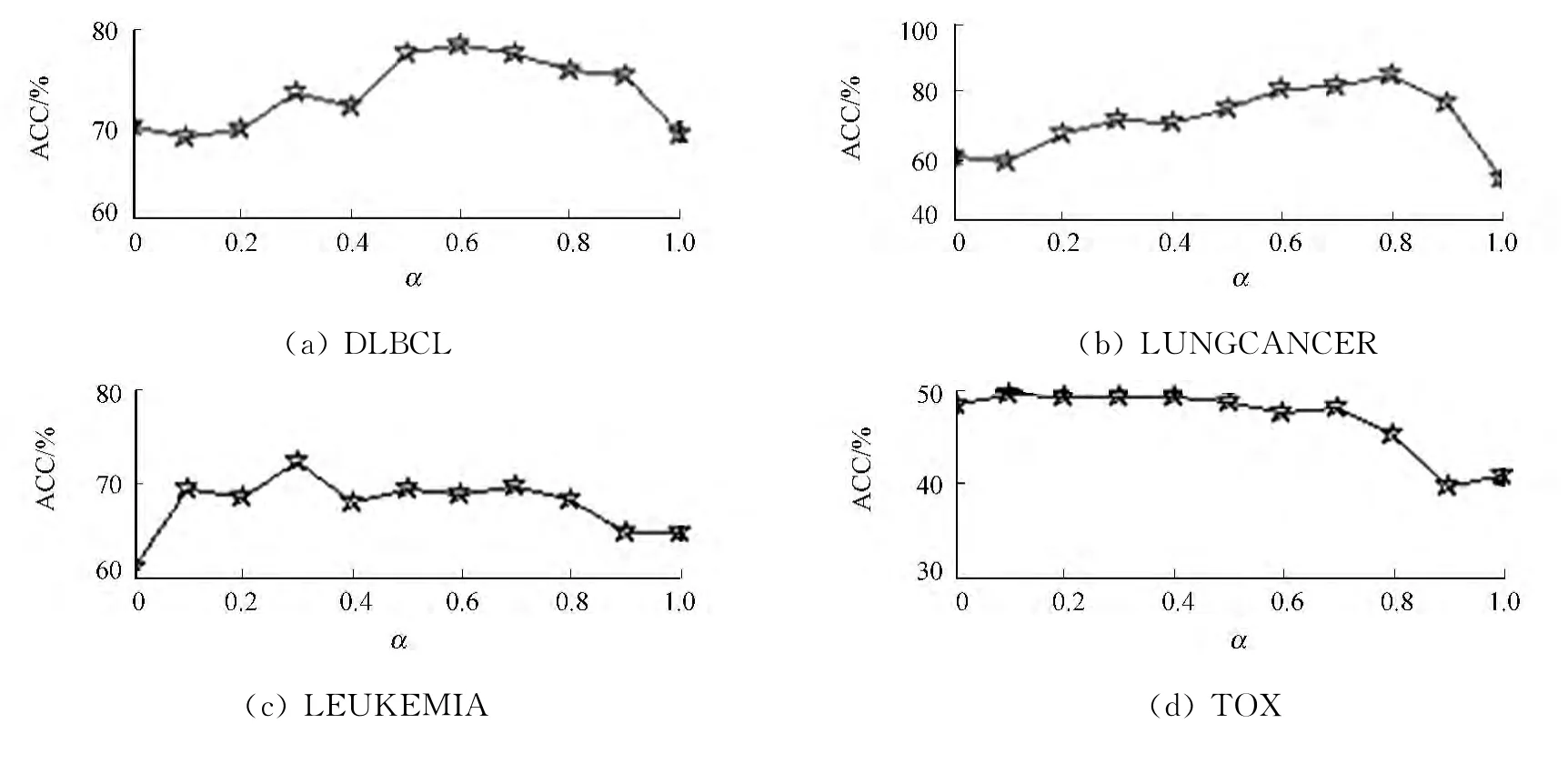
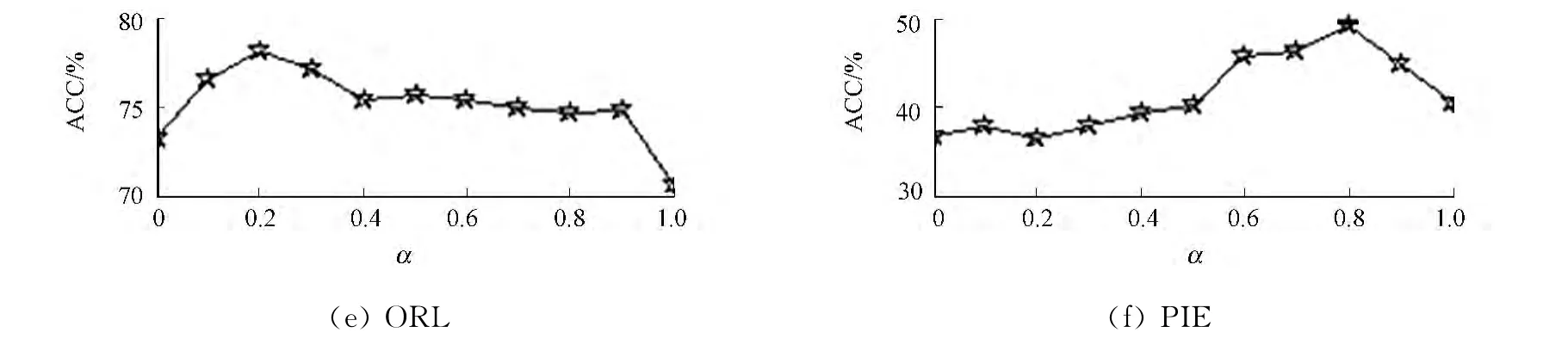
图2 不同α的聚类准确率Fig.2 Clustering accuracy of differentα

4 结束语

提出局部和稀疏保持无监督特征选择法，利用局部保持投影和稀疏保持投影来刻画数据的本质结构，利用L2，1范数的组稀疏性来筛选特征.实验结果表明：LSP是一种有效的无监督特征选择方法.LSP方法的平衡参数α对实验结果有较大的影响，如何自适应地选取该参数将在今后的研究中给出.

［1］徐峻岭，周毓明，陈林，等.基于互信息的无监督特征选择［J］.计算机研究与发展，2012，49（2）：372－382.

［2］张莉，孙钢，郭军.基于K－均值聚类的无监督的特征选择方法［J］.计算机应用研究，2005，22（3）：23－24.

［3］HE Xiao－fei，CAI Deng，NIYOGI P.Laplacian score for feature selection［C］∥Advances in Neural Information Processing Systems.Vancouver：［s.n.］，2005：507－514.

［4］CAI Deng，ZHANG Chi－yuan，HE Xiao－fei.Unsupervised feature selection for multi－cluster data［C］∥Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Washington DC：ACM，2010：333－342.

［5］YANG Shi－zhun，HOU Chen－ping，NIE Fei－ping，et al.Unsupervised maximum margin feature selection viaL2，1－norm minimization［J］.Neural Computing and Applications，2012，21（7）：1791－1799.

［6］FANG Xiao－zhao，XU Yong，LI Xue－long，et al.Locality and similarity preserving embedding for feature selection［J］.Neurocomputing，2014，128：304－315.

［7］GU Quan－quan，LI Zhen－hui，HAN Jia－wei.Joint feature selection and subspace learning［C］∥The 22nd International Joint Conference on Artificial Intelligence.Barcelona：［s.n.］，2011：1294－1299.

［8］HE Xiao－hui，NIYOGI P.Locality preserving projections［C］∥Proceedings of the 17th Annual Conference on Neural Information Processing Systems.Columbia：［s.n.］，2003：153－160.

［9］QIAO Li－shan，CHEN Song－can，TAN Xiao－yang.Sparsity preserving projections with applications to face recognition［J］.Pattern Recognition，2010，43（1）：331－341.

［10］CAI Deng，HE Xiao－fei，WU Xiao－yun，et al.Non－negative matrix factorization on manifold［C］∥Proceedings of International Conference on Data Mining.Pisa：IEEE Press，2008：63－72.