FPGA组合逻辑程序的Petri网建模方法

陈珑，黄颖坤，罗继亮

（华侨大学 信息科学与工程学院，福建 厦门361021）

现场可编程门阵列（field－programmable gate array，FPGA）是一种可编程使用的信号处理器件［1］.FPGA具有灵活性强、时序控制能力强、开发周期短和产品上市速度快等优势［2］，广泛应用于通信、军事、医疗和工业控制等重要领域.然而，FPGA数字系统的分析和设计复杂性随系统规模指数级增长，传统的测试方法难以保证程序的正确性和可靠性，而形式化验证能够枚举验证每一个状态，因此获得了广泛关注［3－5］，形式化验证的前提是形式化建模方法.FPGA系统可以抽象为离散事件系统，Petri网是一种描述离散事件系统的数学模型，较自动机而言，它能够刻画系统的结构信息，具有更高的建模效率.因此，FPGA的Petri网建模方法具有重要研究价值.FPGA的描述语言VHDL（very－high－speed integrated circuit hardware description language）的形式化建模分析主要分为两个方面：一是利用扩展Petri网［6－7］和有色Petri网［8－10］对FPGA系统进行建模，这些扩展是针对某一特定的应用，适用范围比较窄，不具有一般性，并且基于一种Petri网模型的分析方法不能应用到另一种模型上去；二是用变迁描述VHDL中的执行语句，库所表示语句的执行状态，通过托肯的迁移揭示语句的执行过程［11－13］，这些模型是对程序的整体概况描述，分析能力比较差而且无法揭示变量间的逻辑关系.为此，本文提出了一种将描述FPGA组合逻辑电路的VHDL程序转换为普通Petri网的算法.

1 基础知识

1.1 描述组合逻辑电路的VHDL程序

电路的VHDL描述由两大部分组成［14］：1）以关键字entity引导，end entity e＿name结尾的语句部分，称为VHDL的实体，实体描述了电路器件的外部情况及各信号端口的基本性质，如信号流动方向、流动在其上的数据类型等；2）以关键字architecture引导，end architecture a＿name结尾的语句部分，称为VHDL的结构体，结构体描述电路器件的内部逻辑功能和电路结构.

1.2 Petri网［15－16］

普通Petri网是三元组，即N＝（P，T，F），其中，P为状态库所集合，T为变迁集合，F⊆（P×T）∪（T×P）表示库所与变迁之间有向弧的集合.Petri网系统是（N，m0），其中，m0是初始标识.标识是一个向量m∶P→｛0，1，2，…｝，其中，第i维上的分量记作m（Pi），表示状态库所Pi的标识.

2 组合逻辑程序的Petri网设计

针对组合逻辑电路的VHDL程序，程序实体中是一系列逻辑表达式，输入量和输出量抽象为不同的系统状态.控制变量值的变化抽象为一个事件，以变量间的逻辑关系为研究对象，考虑电路零延迟情况下，FPGA组合逻辑程序的Petri网建模方法.

算法1从FPGA组合逻辑程序到普通Petri网的转换算法

输入：组合逻辑电路VHDL程序

输出：Petri网（N，m0）

步骤1在程序实体中找出输入量X1，X2，…，Xn（n∈N＋）和输出量Y1，Y2，…，Ym（m∈N＋），从结构体的描述语句中确定变量间的逻辑函数表达式为

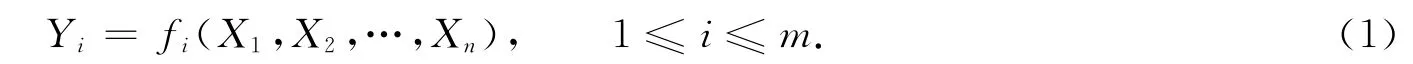
为了叙述简便，以下只以一个逻辑输出表达式进行说明，即

步骤2通过公式法或卡诺图法对式（2）进行化简得到

步骤3对式（3）进行逻辑运算得到

步骤4对式（3）两边同时取非得到

步骤5对式（5）进行化简得到

步骤6对式（6）进行逻辑运算得到

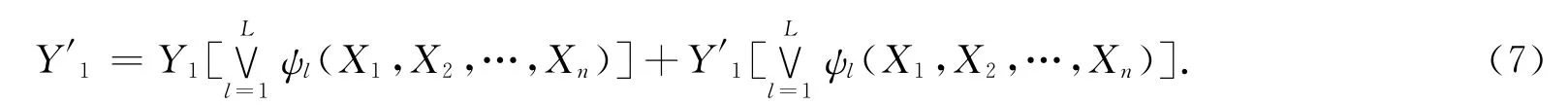
步骤7分别用一对库所表示每个输入量Xj（1≤j≤n）的“0”和“1”两种状态；并在每对库所（PXj0，PXj1）（1≤j≤n）之间分别加上两个变迁ts＋和ts－（1≤s≤n），有向弧集合F＝

步骤8用一对库所表示输出量Y1的“0”和“1”两种状态，并在库所之间加入两个变迁和，有向弧集合

步骤9根据式（4）得出：Y1从当前状态值“0”变为下一个状态值“1”（即当前托肯在状态库所中转移到库所中时）需要项，又存在G个变迁用双向弧把每项Φg（X1，X2，…，Xn）（1≤g≤G）中所涉及的输入量的状态库所与对应的变迁：相连.

步骤10根据式（7）得出：Y′1从当前状态值“0”变为下一个状态值“1”（即当前托肯在状态库所中转移到库所中时）需要项又存在L个变迁用双向弧把每项ψl（X1，X2，…，Xn）（1≤l≤L）中所涉及的输入量的库所与变迁相连接.

3 FPGA组合逻辑系统的状态可达图

系统程序的Petri网模型已经建立，Petri网的动态行为有效模拟了FPGA系统行为，揭示了变量间的逻辑关系.因此，利用Petri网的可达图分析法可以进一步分析程序的运行，便于计算机枚举验证每个状态.但是，Petri网描述的是一个比FPGA系统更复杂的并发系统，理论上只要变迁满足使能条件就能被激发，这样就会生成很多无关状态.为了避免这样的问题，算法2提出了一种可以等价描述FPGA组合逻辑系统运行过程的状态可达图的计算方法.

定义1假设Petri网系统（N，m0）是一个FPGA组合逻辑程序的Petri模型，其中，T＝Tin∪Tout，Te，in⊂Tin，Te，out⊂Tout，Tin和Tout分别是输入和输出变迁集合，Te，in和Te，out分别是可使能的输入和输出变迁集合.

定义2假设三元组GFPGA＝〈M，E，W〉是FPGA组合逻辑系统状态可达图，其中，M＝Min∪Mout，E＝Ein∪Eout.

集合M中的每个节点对应系统的一个状态.其中：Min是以实线圈表示节点的输入状态（由激发输入变迁得到的状态）集合；Mout是以虚线圈表示节点的门级输出状态（由激发输出变迁得到的状态）集合；E是状态节点间的有向边集合；Ein是标有输入变迁的实线有向边集合；Eout是标有输出变迁的虚线有向边集合；W是集合E到T的一个映射，即每条有向边上的变迁标记的集合.

算法2FPGA组合逻辑系统状态可达图生成算法如下.

输入：程序的Petri网系统

输出：GFPGA＝〈M，E，W〉，M＝Min∪Mout，E＝Ein∪Eout

步骤1令Mnew＝Ø，Mold＝Ø，E＝Ø，W＝Ø.

步骤2将初始状态m0标记为“new”，并将｛m0｝→Mnew.

步骤3若未计算的系统状态集合Mnew≠Ø，则继续以下操作；否则算法结束，输出GFPGA＝〈M，E，W〉.

综上所述，引导式护理能有效改善MHD患者疾病认知程度、自护能力、自我效能感、生活质量及管理能力，并减轻其照护家属心理负担，明显降低MHD相关并发症发生率。

步骤4从集合Mnew中任取一个标记为“new”的状态m.

步骤4.1若状态m与可达图已有的其他状态相同，将其标记为“old”，则已计算获得的系统状态集合Mold＝Mold∪｛m｝，然后转向步骤4；若状态m与可达图已有的其他状态不相同，则进行以下操作.

步骤4.2如果在状态m下，没有使能的输入变迁和输出变迁，则将m标记为“dead end”，然后转向步骤4.如果在状态m下存在使能变迁，此时会有两种情况：一种是存在使能的输入变迁且有使能的输出变迁，则跳转到步骤5；另一种是只存在使能的输入变迁，则跳转到步骤6.

步骤5只要可使能的输出变迁集合Te，out＝｛tout｜m［tout〉｝≠Ø，tout∈Tout，就要优先激发所有可使能的输出变迁，生成门级输出状态.

步骤5.1从集合Te，out中任取一个输出变迁tout，激发该变迁，生成输出状态m′out.

步骤5.2将｛m′out｝→Mout，如果输出状态m′out与可达图中已有的状态相同，则Mout＝Mout∪｛m′out｝；否则，从状态m到输出状态m′out之间画一条虚线有向边，则集合Eout＝Eout＋｛〈m，m′out〉｝；并在该虚线上标记输出变迁tout，则有向边上的变迁集合为｛W（〈m，m′out〉）＝tout｝→W，说明在状态m下通过激发输出变迁tout会生成输出状态m′out.

步骤5.4因为标记为“new”的状态m是从集合Mnew中取出的，所以集合Mnew＝Mnew－｛m｝，并返回步骤3.

步骤6当状态m下只存在使能的输入变迁，即Te，in＝｛tin｜m［tin〉｝≠Ø，tin∈Tin，则继续激发一个使能的输入变迁，来改变输入状态.

步骤6.1从集合Te，in中任取一个输入变迁tin，激发该变迁，生成输入状态m′in.

步骤6.2将｛m′in｝→Min，如果m′in与可达图中已有的状态相同，则集合Mold＝Mold∪｛m′in｝；否则从状态m到m′in之间画一条实线有向边，则集合为Ein＝Ein＋｛〈m，m′in〉｝；在该实线上标记输入变迁tin，则有向边上的变迁集合为｛W（〈m，m′in〉）＝tin｝→W，说明在状态m下，通过激发输入变迁tin会生成输入状态m′in.

步骤6.2.1判断输入状态m′in下是否存在可使能的输出变迁，如果m′in下存在可使能的输出变迁，则跳转到步骤6.2.2；否则，跳转到步骤6.2.5.

步骤6.2.2在集合Te，out＝｛tout｜m′out［tout〉｝≠Ø，tout∈Tout中任取一个输出变迁tout，激发该变迁，生成输出状态m″out.

步骤6.2.3将｛m″out｝→Mout，如果m″out与可达图中已有的状态相同，则集合Mold＝Mold∪｛m″out｝；否则，从状态m′in到m″out之间画一条虚线有向边，则集合为Eout＝Eout＋｛〈m′in，m″out〉｝；在该虚线上标记输出变迁tout，则集合为｛W（〈m′in，m″out〉）＝tout｝→W，说明在输入状态m′in下，通过激发输出变迁tout会生成输出状态m″out.

步骤6.2.4集合Te，out＝Te，out－｛tout｝.判断输入状态m′in下的集合Te，out是否为空集，如果可集合Te，out≠Ø，即存在使能的输出变迁，那么返回步骤6.2.2；如果集合Te，out＝Ø，即不存在使能的输出变迁，则继续以下操作.

步骤6.2.5因为在状态m下从集合Te，in中取走了一个使能输入变迁tin，所以Te，in＝Te，in－｛tin｝.判断集合Te，in是否为空集，如果集合Te，in≠Ø，即存在使能的输入变迁，那么返回步骤6.1；如果集合Te，in＝Ø，即不存在使能的输入变迁，则继续以下操作.

步骤6.3未计算的系统状态集合Mnew＝Mnew－｛m｝，并返回步骤3.

在算法2中，〈m，m′out〉表示从状态m指向m′out的一条有向边，W（〈m，m′out〉）＝tout表示在状态m下通过激发变迁tout得到m′out.Mnew是未计算的状态集合，Mold是已计算获得的状态集合.当Mnew中某个可达状态被计算获得，则将其从Mnew中剔除并添加到Mold中，直至Mnew为空集，算法结束.

根据算法2可知：在某个电路状态下，如果同时存在使能的输入变迁和输出变迁，应当优先激发该电路状态下所有的输出变迁，得到一个稳定的门级输出状态；如果在某个电路状态下，只存在使能的输入变迁，则激发一个输入变迁，得到一个稳定的输入状态，通过改变输入量的取值，再判断该输入状态下是否存在使能的输出变迁.

4 实例分析

某化工原料生产反应釜，如图1所示.系统启动后，当液位低于S1，V1打开，注入原料A；当液位到达S1，V1关闭，同时打开V2阀，注入原料B；当液位到达S2，V2关闭，启动M加热；当温度值到达S3，M停止加热，同时打开V3阀，并且L启动计时；一段时间后，定时器L关闭，V3关闭，系统回到最初状态.根据系统要求，某程序员给出图1所示反应釜控制系统的部分VHDL程序，如图2所示.

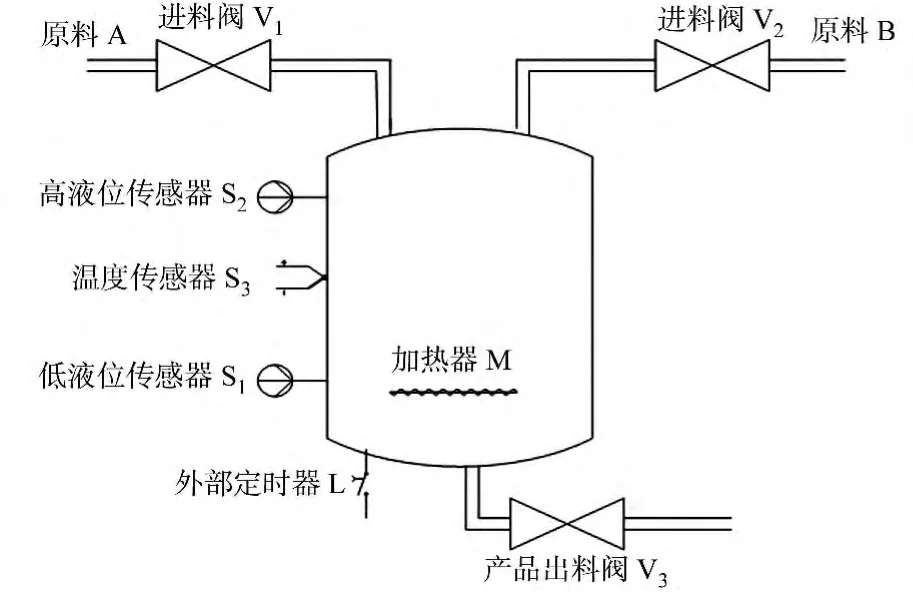
图1 某化工原料生产反应釜 Fig.1 A chemical raw materials production reactor

图2 反应釜控制系统的部分VHDL程序Fig.2 A part of VHDL program of the reactor

根据算法1，针对图2的反应釜控制系统程序，首先将程序中的每个变量分别用一对库所表示，抽象为运行（on）和休息（off）状态，即逻辑上表示“1”和“0”两个状态；其次在输入变量的库所间加上输入变迁，在输出变量的库所间加上输出变迁；然后根据逻辑表达式所描述的输出量与输入量间的逻辑关系，描述出输入量库所与输出变迁间的控制关系；最后由算法1，将图2的系统程序转换为图3的Petri网模型.根据算法2，由反应釜控制系统的Petri网模型，从某个初始状态开始，分别计算出每个输入状态下所对应的稳定的输出状态，得到如图4所示的系统状态可达图.由图4分析可知：系统具有可逆性和活性，其中每个状态的表现形式为

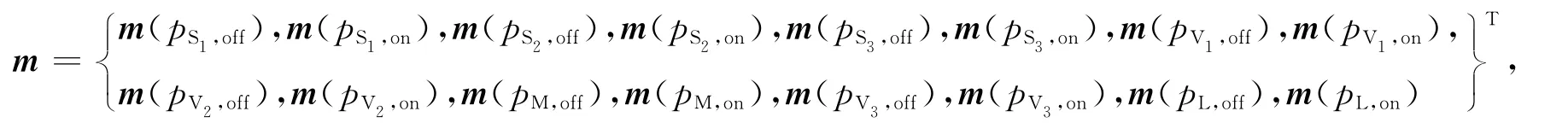
部分状态标识为

图3 反应釜控制系统的Petri模型 Fig.3 Petri net model of the reactor control system

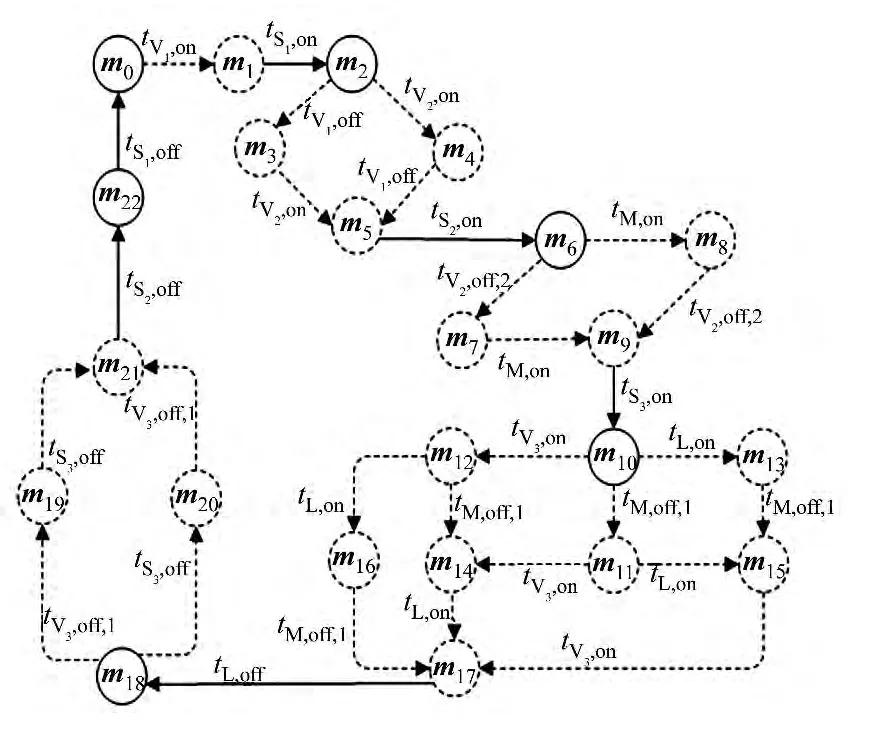
图4 反应釜控制系统的Petri网模型的状态可达图Fig.4 State reachable graph of Petri net model for the reactor control system

5 结束语

提出了一个完整的将FPGA组合逻辑程序自动转换为普通Petri网的方法，与现有基于扩展Petri网的建模方法相比，文中基于普通Petri网的建模方法更具一般性，应用范围更广，对于系统变量间的逻辑功能关系有更强的分析能力.另外，在考虑电路零延迟的情况下，根据已建好的程序Petri网模型，通过定义新的变迁激发规则，建立一个可以等价描述FPGA组合逻辑系统运行过程的状态空间，去掉一些无关的中间状态，指数级地压缩状态空间，为后续的形式化验证［17－18］提高效率.后续工作将利用计算机通过系统状态可达图对程序进行形式化验证，检测存在逻辑错误的系统程序.

［1］王芯，孙富明，李磊，等.FPGA设计安全性综述［J］.小型微型计算机系统，2010，31（7）：1333－1335.

［2］杨海钢，孙嘉斌，王慰.FPGA器件设计技术发展综述［J］.电子与信息学报，2010，32（3）：716－718.

［3］王彦本.集成电路形式化验证方法研究［J］.电子科技，2008，21（8）：4－7.

［4］GHARBI A，KHALGUI M，BEN A S，et al.Optimal model checking of safe control embedded software components［C］∥15th Conference on Emerging Technologies and Factory Automation.Bilbao：IEEE Press，2010：1－8.

［5］PATIL S，VYATKIN V，SOROURI M，et al.Formal verification of intelligent mechatronic systems with decentralized control logic［C］∥17th Conference on ETFA.Krakow：IEEE Press，2012：1－7.

［6］古天龙.组合逻辑电路的Petri网仿真分析［J］.系统仿真学报，1994，6（2）：32－36.

［7］TSAI J I，TENG C C，LEE C H.Test generation and site of fault for combinational circuits using logic Petri－nets［C］∥International Conference on Systems Man and Cybernetics.Taipei：IEEE Press，2006：8－11.

［8］欧阳星明，胡青海.基于有色Petri网的逻辑电路仿真模型设计［J］.华中科技大学学报：自然科学版，2006，34（3）：18－20.

［9］BUKOWIEC A，ADAMSKI M.Synthesis of Petri nets into FPGA with operation flexible memories［C］∥15th International Symposium on Design and Diagnostics of Electronic Circuits and Systems.Tallinn：IEEE Press，2012：16－21.

［10］KOKASH N，ARBAB F.Formal design and verification of long－running transactions with extensible coordination tools［J］.IEEE Transactions on Services Computing，2013，6（2）：186－200.

［11］OLCOZ S，COLOM J M.A Petri net approach for the analysis of VHDL descriptions［M］.Berlin Heidelberg：Springer，1993：15－26.

［12］WALTER D，LITTLE S，SEEGMILLER N，et al.Symbolic model checking of analog／mixed－signal circuits［C］∥Asia and South Pacific Design Automation Conference.Yokohama：IEEE Press，2007：316－323.

［13］MOUTINHO F，GOMES L.State space generation algorithm for gals systems modeled by IOPT Petri nets［C］∥37th Annual Conference on Industrial Electronics Society.Melbourne，VIC：IEEE Press，2011：7－10.

［14］藩松，黄继业.EDA技术与VHDL［M］.北京：清华大学出版社，2009：42－47.

［15］LUO Ji－liang，NONAMI K.Approach for transforming linear constraints on Petri nets［J］.IEEE Transactions on Automatic Control，2011，56（11）：2751－2765.

［16］DAVID R，ALIA H.Discrete continuous and hybrid Petri nets［M］.Berlin Heidelberg：Springer，2005：24－40.

［17］SCHWARICK M，ROHR C，HEINER M.MARCIE－model checking and reachability analysis done efficiently［C］∥8th Conference on Quantitative Evaluation of Systems.Aachen：IEEE Press，2011：91－100.

［18］KHALGUI M，MOSBAHI O，LI Z W，et al.Reconfigurable multiagent embedded control systems：From modeling to implementation［J］.IEEE Transactions on Computers，2011，60（4）：538－551.