采用线性预测模型的语音篡改检测

林晓丹

（华侨大学 信息科学与工程学院，福建 厦门361021）

近年来，由于数字录音设备的广泛应用和音频编辑处理技术的发展，编辑数字录音变得非常容易.非专业人士也可以轻而易举地修改音频内容而不留下痕迹.数字录音作为法庭举证中一项非常重要的证据，可能被非法篡改.如果这些伪造音频被利用，将严重影响司法判决的公正.尽管数字签名和数字水印技术也能为音频的真实性和完整性提供保障，但现有的录音设备大多无法预先嵌入水印或签名信息，因此，数字语音盲取证技术变得迫在眉睫［1］.现有的音频盲取证主要着眼于以下4个方面：1）基于电网频率的分析［2］，这是目前最有效的音频盲取证方法，但对使用电池供电的录音设备，例如MP3、录音笔、手机等，这种检测方法失去了其有效性；2）基于录音环境的分析［3－4］；3）针对特定类型篡改的检测［5－7］；4）分析音频统计特性的变化［8］.目前，多数录音设备直接录制的音频都是wav格式的数字音频文件，以原始的波形文件作为检测对象，由于插入、替换、删除、拼接操作，导致音频前后样点相关性减弱，线性预测残差与原始音频的残差相比出现明显差异.因此，本文通过分析原始音频和篡改音频的线性预测残差，在对残差信号进行统计分析的基础上，提出一种能够检测并定位篡改位置的语音盲取证方法.

1 线性预测残差分析

1.1 线性预测模型

线性预测的基本思想是用若干个过去的语音取样的线性组合来预测当前的语音样值.1个p阶的线性预测模型可表示为

式（1）中：p为预测阶数；s（n）对应n时刻输入的语音样点；ai为线性预测系数（LPC）；（n）为线性预测方法对s（n）的估值.线性预测误差（n）为

线性预测模型的关键在于预测系数ai的求解.通过使预测误差的均方值最小，即满足E［（n）］2最小，可解得ai.求取ai的过程中，采用Levinson－Durbin递推算法对Yule－Walker方程组求解，即

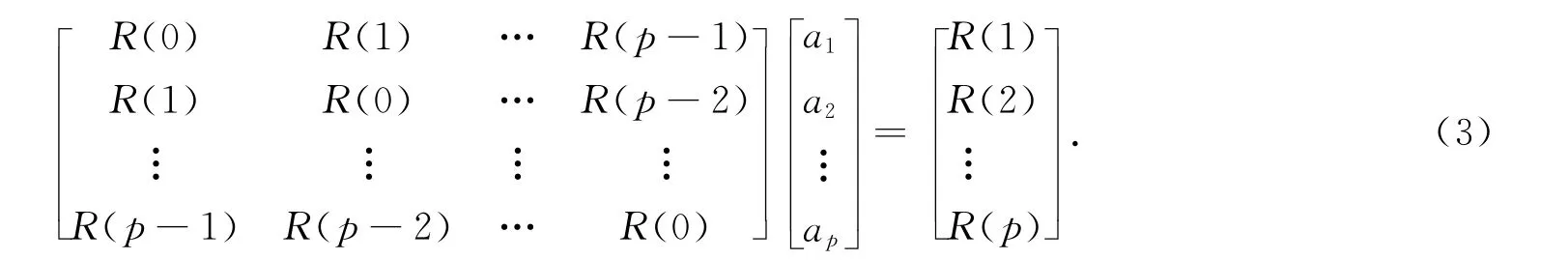
式（3）中：R（m）＝E［s（n＋m）s（n）］为s（n）的自相关序列.

预测系数ai可以准确捕获说话人的声道特征，对于录音信号的篡改痕迹，同样可以体现在预测系数上.语音信号在短时间内具有较大的相关性，对语音的篡改操作必然会破坏前后样点的相关性，篡改音频在频谱上也将出现明显的不连续性，最终导致在篡改位置预测系数无法准确表征语音的频谱幅度.线性预测阶数为13时，对一段语音的预测结果如图1所示.由图1可知：未发生篡改时，线性预测结果能够准确跟踪输入语音的变化；而对于篡改语音，预测结果则无法准确跟踪其变化情况，产生较大的预测误差.为了克服语音能量变化的影响，将线性预测残差信号归一化，即其中：Ep为求解线性预测系数ai时得到的最小均方误差.

图1 语音线性预测结果Fig.1 Linear prediction results of the speech

1.2 线性预测残差信号分析

对于原始的语音信号，在计算线性预测系数的过程中，语音信号的短时相关性已被大部分去除，可认为预测残差和语音信号无关.理论上，理想的残差信号应具有平坦的功率谱.然而，上述结论只有当残差信号为零均值，且预测阶数足够高的前提下才成立.采样率均为16kHz的原始语音和篡改语音LPC残差信号的频域解释，如图2所示.图2中：S（f）为功率谱.由图2（a）可知：即使语音未遭受篡改，其预测残差也不具有平坦的功率谱；残差信号包含的谐波分量非常明显，其频率ωm是语音基频ω0的整数倍，即ωm＝m·ω0.考虑到实际录音环境和录音设备可能存在噪声，原始语音的线性预测残差信号e（n）表示为.其中：am，θm分别为谐波幅度和相位；M为残差信号中的谐波数目；w（n）为环境噪声，其带宽为Bw.

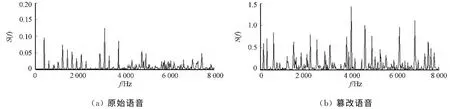
图2 语音线性预测残差信号功率谱对比Fig.2 Power spectrums of LPC residual of the speech

由图2（b）可知：篡改处的不连续性使预测残差出现了许多新的频率分量，这些频率分量可能包含新的基音频率，例如，拼接、替换、插入操作引入新的谐波分量.这时残差信号包含原语音的谐波分量、环境噪声及篡改引入的随机噪声c（n）.其中：c（n）包含的频率成分与原语音的基频无关.新的谐波分量不单独列出，也包含于c（n）中.因此，篡改语音的残差表示为θ′m）.其中：篡改语音中原语音残差的谐波数目、幅度和相位可能发生变化，分别记为N，a′m和θ′m.

2 篡改检测

2.1 残差信号的高阶统计特征

盲检测方法没有原始的语音信号作为参考，且可能存在录音环境和设备噪声，因此，仅从语音信号功率谱的变化情况很难判断是否出现了篡改.从信号的统计特性出发，对残差信号进行分析.

如果x（n）是零均值随机序列，其三阶和四阶累积量为γ3＝E｛x3（n）｝＝m3｛0，0｝，γ4＝E｛x4（n）｝－3E2｛x2（n）｝＝m4｛0，0，0｝－3m22（0）.x（n）的偏度和峰度分别用三阶和四阶累积量测定，即α＝

语音的谐波分量主要集中在中低频范围内.图2（a）中：原始语音的谐波主要集中在0～4 000Hz的频带内，这些谐波分量的高阶累积量不为零，将对检测产生干扰.因此，先对残差信号进行带通滤波.带通滤波器的冲激响应为h（n），带宽为Bm.残差信号e（n）通过带通滤波器后，谐波分量大部分被滤除.因此，原始语音e0（n）和篡改语音通过滤波器的残差信号et（n）分别表示为e0（n）＝BPF［w（n）］，et（n）＝BPF［w（n）＋c（n）］.其中：BPF为带通滤波.通常环境噪声w（n）具有较大的带宽，即Bw≫Bm.因此，残差信号e0（n）为具有高斯分布的窄带信号，e0（n）的高阶统计量为0.而篡改信号由于c（n）的存在，et（n）具有明显的高阶统计量.带通滤波后原始语音和篡改语音残差信号的分布直方图，如图3所示.图3中：N为频次.在对大量语音片段测试后发现：et（n）的直方图具有更尖锐的峰值和更长的拖尾，符合超高斯分布的特性，且e0（n）的分布直方图更接近高斯特性.

图3 残差信号分布直方图Fig.3 Histograms of residual LPC

2.2 语音篡改检测

将待检测的语音信号进行分帧，对语音帧进行预加重、加窗处理，计算各帧的归一化线性预测残差.第i帧残差信号通过上述带通滤波器的输出记为ei（n），对ei（n）进行高阶累积量分析.利用偏度和峰度联合特征作为是否篡改的判断依据.根据上述分析，若未经篡改，ei（n）的偏度和峰度应接近于零，而篡改语音由于明显的非高斯特性，其偏度和峰度均偏离零值.因此，计算第i帧ei（n）的偏度和峰度，分别记为α（i），β（i），设置合适的阈值λ1，λ2即可进行判断.若｜α（i）｜＞λ1，且β（i）＞λ2，则认为在该帧位置发生了篡改.

3 实验结果及分析

为检验算法的有效性，将文中算法性能与文献［7］进行比较.采用PC机（连接外置麦克风）、手机、录音笔、MP3，共录制了4种不同采样率的音频，各为44.1，32.0，16.0，8.0kHz，每种采样率男声和女声各25段.从TIMIT语音库选取100段语音（16kHz），将其采样率转换成44.1，32.0，8.0kHz，即每种采样率各100段.此外，从互联网下载了如上4种采样率的音频各50段.测试集中每种采样率的未篡改语音各200段，选取4种采样率的音频各100段分别进行随机删除、拼接、替换和插入，篡改后音频保持采样率不变，每种采样率的篡改音频各400段.将上述所有篡改和未篡改音频作为测试集（共2 400段语音）.虚警率（原始音频误判为篡改音频）和漏警率（篡改音频误判为原始音频）分别记为ηFP，ηFN.

实验中发现线性预测阶数越高，残差信号的相关性越小，检测准确率越高.然而，当预测阶数高达13时，随着预测阶数的增大，检测性能无明显提高.因此，选取线性预测阶数为13，帧长20ms，两帧之间有50%重叠.设置带通滤波器中心频率为fs／4＋500，其中：fs为音频采样频率，带宽Bm为1 000 Hz.实验中λ1，λ2越大，漏警率越高.若λ1，λ2过小，则虚警率也随之增大，实验选取检测阈值λ1＝0.03，λ2＝1.5.不同采样率下文中算法与文献［7］的检测性能，如表1所示.由表1可知：与文献［7］相比，文中的检测准确率有所提高.由于文中算法中各帧的时长相同，采样率越高，语音帧包含的样点数越多，残差信号的相关性越小.因此，检测准确率随采样率的增大而提高.

表1 不同采样率下检测性能比较Tab.1 Detection results under different sample rates compared with method in［7］

3.1 篡改定位结果

图4，5分别为两段不同的篡改语音.图6，7分别为对应于上述篡改语音的残差信号经带通滤波后的偏度和峰度.由图6可知：第99帧和第300帧的｜α（i）｜和β（i）均高于所设阈值.因此，可判断在该位置发生了篡改.由图7可知：在第300帧附近发生了篡改.

图4 原始语音与篡改语音1Fig.4 Original and tampered signal 1

图5 原始语音与篡改语音2Fig.5 Original and tampered signal 2

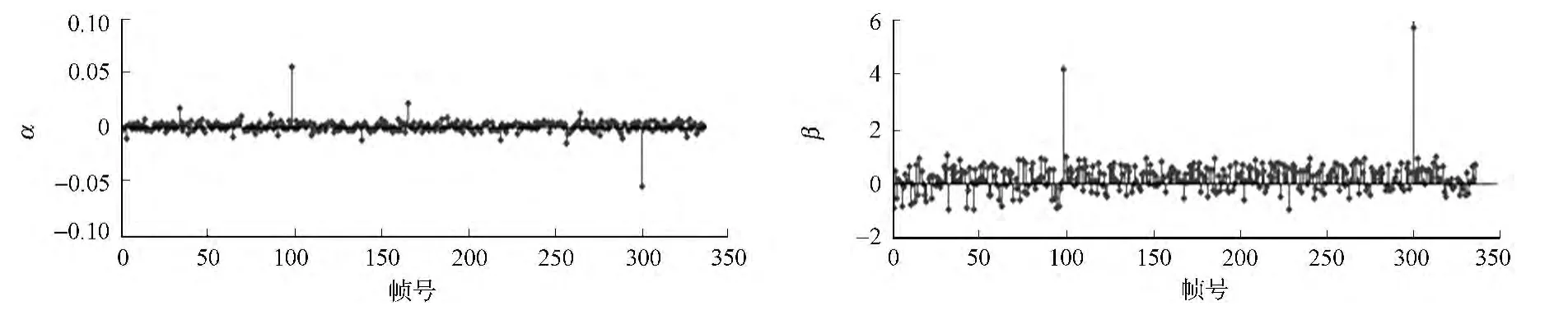
图6 篡改定位结果1Fig.6 Forgery detection result 1

图7 篡改定位结果2Fig.7 Forgery detection result 2

3.2 背景噪声对检测结果的影响

为了检验文中方法对噪声的鲁棒性，对上述音频添加不同强度的背景噪声.噪声由Adobe Audition软件生成，包含两类噪声（白噪声和粉色噪声），用于模拟环境噪声.调整噪声强度，从而得到不同信噪比的含噪语音.选取每种采样率下的含噪语音各100段，分别进行随机删除、插入、替换、拼接，检测结果如表2所示.表2中：RSN为信噪比.由表2可知：文中方法考虑了噪声的统计特性，因此，检测鲁棒性更高.

表2 不同信噪比时的检测性能比较Tab.2 Detection performance under different noise conditions compared with method in［7］

4 结束语

分析了语音信号的线性预测模型残差，并将残差信号的统计特性用于语音的被动取证.原始音频LPC残差信号的高阶累积量几乎为零，而篡改音频的预测残差体现出明显的超高斯特性，其高阶累积量偏离零值.实验结果表明：文中方法对于语音的插入、删除、替换、拼接具有较高的检测可靠性，而且可以准确定位出篡改位置；与现有算法比较，在噪声环境中，文中方法的检测鲁棒性更好.

［1］SWATI G，SEONGHO C，KUO C C J.Current developments and future trends in audio authentication［J］.IEEE Multimedia，2012，19（1）：50－59.

［2］LIU Yu－ming，YUAN Zhi－yong，MARKHAM P N，et al.Application of power system frequency for digital audio authentication［J］.IEEE Transactions on Power Delivery，2012，27（4）：1820－1828.

［3］MALIK H，FARID H.Audio forensics from acoustic reverberation［C］∥IEEE International Conference on Acoustics，Speech，and Signal Processing.Dallas：IEEE Press，2010：1710－1713.

［4］IKRAM S，MALIK H.Digital audio forensics using background noise［C］∥IEEE International Conference on Multimedia and Expo.Singapore：IEEE Press，2010：106－110.

［5］QIAN Shi，MA Xiao－hong.Detection of audio interpolation based on singular value decomposition［C］∥Awareness Science and Technology.Dalian：［s.n.］，2011：287－290.

［6］YANG Rui，QU Zhen－hua，HUANG Ji－wu.Exposing MP3audio forgeries using frame offsets［J］.ACM Transactions on Multimedia Computing，Communications，and Applications，2012，33（8）：1－20.

［7］CHEN Jiao－rong，XIANG Shi－jun.Exposing digital audio forgeries in time domain by using singularity analysis with wavelets［C］∥Proceedings of the First ACM Workshop on Information Hiding and Multimedia Security.New York：［s.n.］，2013：149－158.