1种航空发动机增广模型的建立方法

党 伟，王华威，王 曦，杨舒柏，张 耿

（北京航空航天大学能源与动力学院,北京100191）

0 引言

目前，航空发动机多变量控制系统的设计与故障诊断往往只针对发动机线性模型而忽略其执行机构，或者简单的用1阶惯性环节模拟，这种近似处理直接影响着控制器的设计品质和实际工程应用：一方面，执行机构对控制器输出的控制能量具有约束作用，忽略该作用设计的控制器往往没有工程实用价值[1]；另一方面，执行机构的很多特征信息如控制压力等也不能得到体现，损失了很多关键信息而无法对执行机构进行有效的故障诊断以实现容错控制。因此，建立精准的包含执行机构的增广发动机状态变量模型是十分必要的。当前线性模型的提取主要集中于发动机的小偏差状态变量模型，提取方法主要有小扰动法[2]和系统辨识法[3]。小扰动法方法简单但建模精度不高，系统辨识法则可以明显增加建模的精度，得到了不断发展。仇小杰[4]提出了基于变尺度法的混合求解方法；李秋国等[5]提出了基于遗传算法的发动机状态变量模型求解方法；王斌等[6]提出了1种基于粒子群算法建立小偏差状态变量模型的方法并以此为基础建立了分段线性模型。但这些方法都存在初值选取问题，并且容易陷入局部最优，在建立LPV模型时容易出现插值异常[7]等现象。而以航空发动机液压执行机构为对象的状态变量模型的提取鲜有研究，少数研究航空液压系统的文章主要使用理论推导的方法得到其传递函数，但其推导复杂，且缺少液压系统的状态变量，不适用于液压系统的故障诊断。

针对以上问题，提出了1种使用差分进化算法[8]提取包含发动机及其执行机构的增广发动机状态变量模型的方法，并建立了完整且具有一般性的发动机增广模型。

1 发动机状态变量模型的建立

精确的航空发动机小偏差状态变量模型可用于LPV模型[9]的建立及在其基础上进行增益调度控制器的设计。本文以某喷口可调的双轴涡扇发动机部件级非线性模型数据为基础，在稳态工作点上使用差分进化算法对非线性数据进行了最小二乘拟合，建立了精确的航空发动机的小偏差状态变量模型。

1.1 差分进化算法

差分进化算法计算效率高，对初值不敏感，具有很强的全局收敛性和鲁棒性[10]，是遗传算法的变种，其原理简单易实现、收敛速度快，是1种不需要初始信息就可以寻求全局最优解的高效的优化方法。其思想是基于种群内的个体差异度生成临时个体，然后随机重组实现种群进化，因此该算法具有很好的全局收敛性和鲁棒性。差分进化算法包括初始化、变异操作、交叉操作和选择操作几部分[11]。具体流程如图1所示。

图1 差分进化算法流程

差分进化算法中的设置参数如种群数量NP、变异算子F、交叉算子CR等的选取依据一些经验规则[12-13]，对差分进化算法的性能有重要影响。

1.2 提取发动机状态变量模型过程

由于发动机容腔中压力和温度的动态比转子转速快得多，因此可只以发动机转子转速作为状态量，由此建立的航空发动机小偏差状态变量模型为

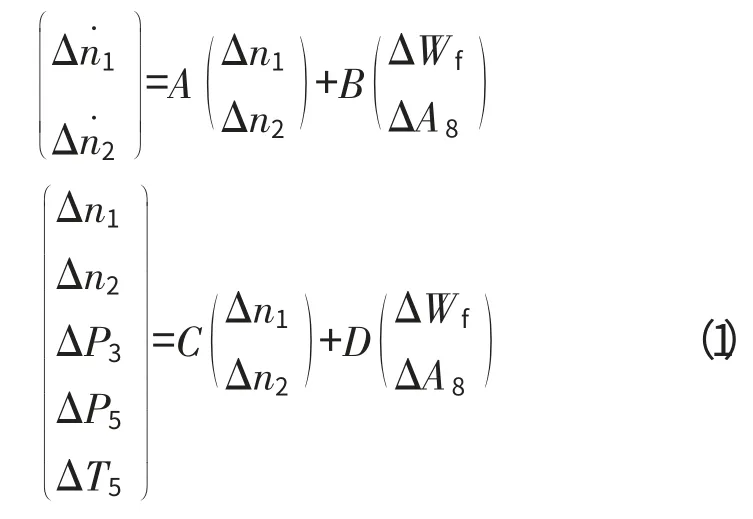
式中：n1为风扇转速，r/min；n2为高压转子转速，r/min；Wf为主燃油流量，kg/h；P3为高压压气机后总压，MPa；P5为低压涡轮后总压，MPa；T5为低压涡轮出口总温，K。

使用差分进化算法提取发动机小偏差状态变量模型的具体步骤如下：

（1）在发动机非线性系统稳态工作点上对控制输入Wf和A8分别作小阶跃，得到非线性模型动态响应的偏差信号

（2）用随机数程序选取初值A0、B0、C0、D0，矩阵中每个元素的范围取为[-10，10]。由于初值在范围内任意选取，优化前对初值进行稳定性判断，保证其特征值在复平面的左半平面。

在本例中，种群数量NP=80，变异因子F =0.95，交叉因子CR=0.9，最大迭代次数G=100，仿真步长δT=0.02s，仿真时间T=4s。

（3）对发动机线性模型控制输入Wf和A8作与非线性模型同样大小的阶跃响应，得到线性模型动态响应的偏差信号

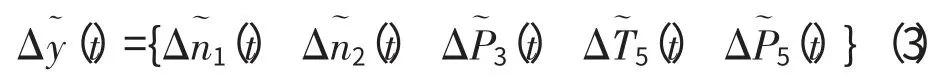
即计算与部件级非线性模型响应偏差平方和最小的线性模型系数矩阵。通过优化，得到满足要求的A、B、C、D。其中，n=T/δT=200。

发动机非线性模型与状态变量线性模型在H=0，Ma=0，Wf=1.046kg/s，A8=1883cm2的稳态点上油量和喷口面积分别向下作2%阶跃，使用差分进化算法进行辨识，结果检验差分进化算法提取的线性模型的精确度，并加入小扰动法提取的状态变量模型进行对比，喷口面积阶跃变化时输出变量曲线和主燃油阶跃变化时输出变量曲线的对比结果分别如图2、3所示。

从仿真结果来看，差分进化方法优化算出的线性模型不仅与非线性模型动态过程吻合良好，而且能保证发动机最终稳定值的一致性，具有很高的精度。而小扰动法不能保证终值的一致性，这是因为该方法对发动机某一控制量或者状态量作小扰动时强制保证其他状态量和控制量不发生变化，而实际上对任一状态量或控制量作小扰动时必会引起其他状态变量的变化。发动机中的2个状态量风扇转速和高压转子转速耦合性很强，小扰动法强行解耦造成了较大的建模误差。

图2 主燃油阶跃变化时输出变量曲线

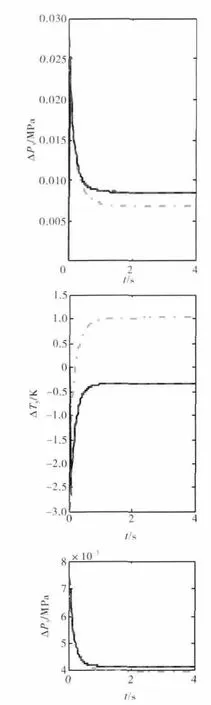
图3 喷口面积阶跃变化时输出变量曲线

2 执行机构状态变量模型的建立

通常在航空发动机控制器的设计过程中，往往忽略执行机构的影响，或者简单的将执行机构用惯性环节近似，实际上执行机构包含有非线性环节。在控制系统设计时主要体现在对控制输入的约束及位置、饱和速率等问题。这些饱和限制要求控制器具有抗饱和性能。

执行机构的线性模型有频域传递函数模型和时域状态变量模型2种。频域传递函数模型一般通过理论推导获得，适用于经典控制理论分析；而状态变量模型适用于多输入多输出系统，且包含了大量的中间变量，系统信息全面，适用于执行机构的故障诊断和容错控制。因此精确提取执行机构状态变量模型已成为目前液压执行机构系统研究的重点。传统建立发动机执行机构传递函数模型的方法为小偏差线性化法[14]，其推导过程复杂，工作量大。而利用差分进化算法对初值不敏感这个特点，对某双轴喷口可调涡扇发动机的2个主要的执行机构即主燃油计量机构和喷口面积调节机构进行系统辨识，得到其精确的状态变量模型。为了使执行机构模型适用于基于现代控制理论的如Kalman滤波器和未知输入观测法（UIO）等故障诊断方法，选取了较多的状态变量，建立了相对精确的高阶执行机构状态空间模型。

2.1 主燃油计量机构状态变量模型的建立

主燃油计量机构为液压机械系统包括随动活塞和计量活门2部分，如图4所示。占空比信号的变化使随动活塞的上腔压力发生变化，从而使随动活塞上下移动，进而控制计量活门的开度，以提供所需油量。占空比信号在50%时系统处于平衡状态，随动活塞位于整个滑阀的中间位置。

图4 主燃油计量执行机构原理

建立主燃油计量机构的AMESim[15]模型如图5所示。在平衡位置的基础上给控制输入占空比信号1个小阶跃，如图6（a）所示；伺服活塞上腔压力，伺服活塞的位移、速度的输出响应分别如图6（b）、（c）、（d）所示。

利用差分进化算法，对3条输出响应曲线进行拟合，每个矩阵元素的取值范围为[-1e61e6]，由于搜索范围变大，将差分进化算法的参数调整为：种群数量NP=150，变异因子F=1.2，交叉因子CR=0.9，最大迭代次数G=100。得到主燃油计量机构的状态变量模型

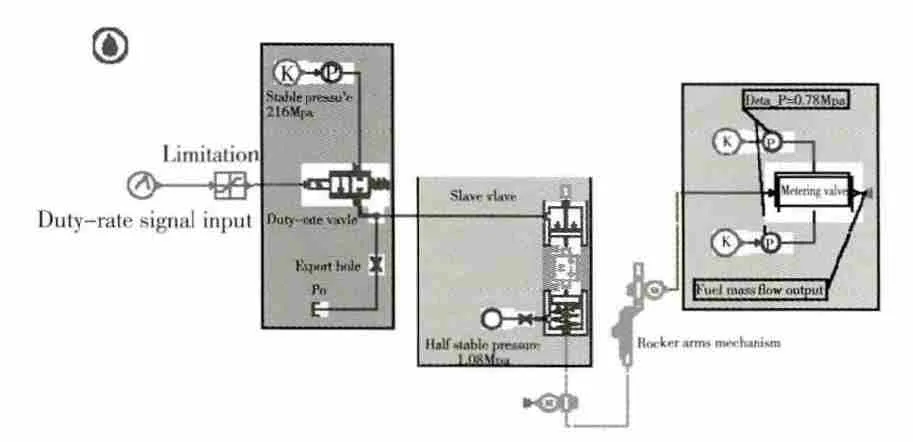
图5 主燃油计量执行机构AMEsim模型

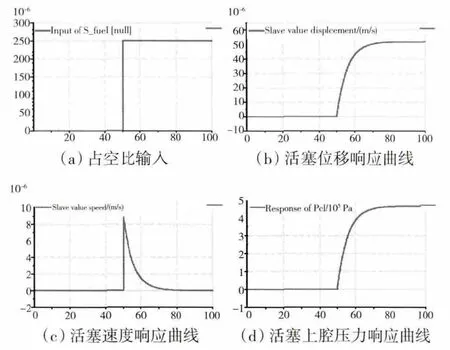
图6 SFuel变化时状态量的变化曲线

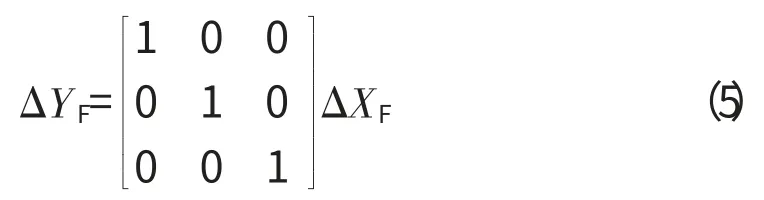
式中：状态变量XF=[x v Pcl]T；x 随动活塞的位移，m；v 为随动活塞的运动速度，m/s；Pcl为随动活塞控制腔即上腔压力，105Pa；SFuel为主燃油计量阀占空比信号的大小。

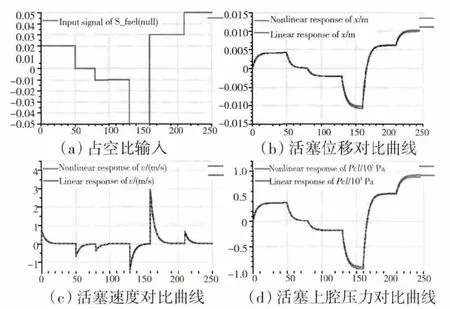
图7 滑阀在整个行程运动时各状态量的变化曲线

滑阀在整个行程运动时各状态量的变化曲线如图7所示。从图中可见，在平衡位置的基础上改变控制输入SFuel使随动活塞在整个行程内变化时，非线性模型与上述提取的状态变量模型在随动活塞位移、移动速度及控制腔压力等方面的变化对比。随动活塞在整个工作范围内，非线性模型与线性模型的偏差很小，因此可用式（5）的状态空间方程表示整个工作范围内主燃油计量机构的特性。另外，由于液压作动器模型的最一般形式为3阶，同时包括活塞惯性和流体压缩性效应[16]，因此所建立状态变量模型为全阶模型。

2.2 喷口面积作动器状态空间模型的建立

喷口面积调节机构由分油活门和模拟作动筒组成，结构原理如图8所示。占空比信号的变化使分油活门上腔的压力变化，进而使得分油活门滑阀移动；分油活门滑阀位移变化又使高低压油通往作动筒2腔的流通面积变化，在作动筒两端产生压力差使其移动，带动喷口面积大小变化。

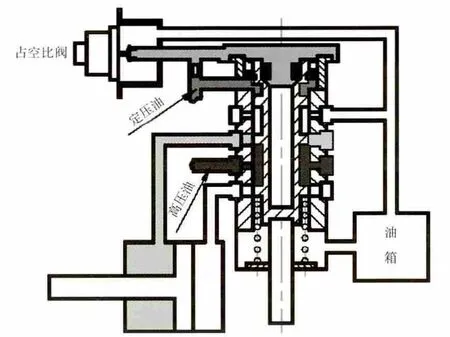
图8 喷口面积调节机构原理

根据其工作原理建立AMESim非线性模型如图9所示。注意，在上述模型中未包含施加在活塞连杆机构上的负载。在平衡位置的基础上给控制输入占空比信号1个小阶跃，如图10（a）所示；分油活门活塞的位移、速度、控制腔压力以及作动筒的移动速度、位移的输出响应如图10（b）~（f）所示。

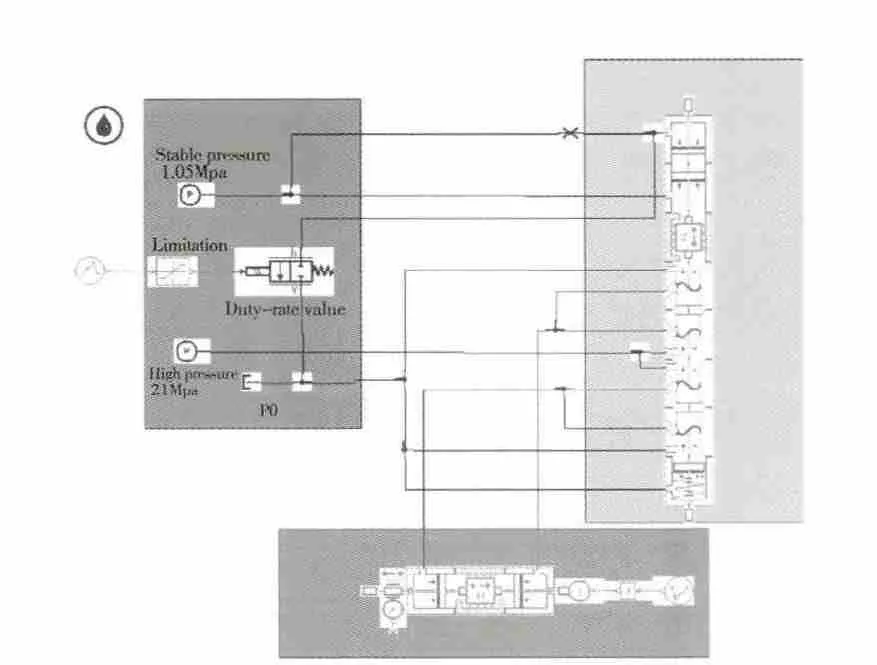
图9 喷口面积作动器AMESim模型

图10 SNozzle变化时状态量变化曲线

通过差分进化算法利用图10的输入输出非线性数据进行最小二乘拟合，差分进化算法参数同主燃油计量活门部分，可求出其状态空间方程为

式中：YN=XN=[x1v1Pc/lv2x2]T；x1为分油活门阀芯位移，m；v1为分油活门阀芯移动速度，m/s；Pc/l为分油活门控制腔压力，105Pa；v2为作动筒活塞移动速度，m/s；x2为作动筒活塞位移，m；SNozzle为喷口面积作动器占空比输入信号。

喷口作动筒在行程内变化时状态变量变化曲线如图11所示。从图中可见，在平衡位置的基础上改变控制输入SNozzle使作动筒活塞在整个行程内变化时，非线性模型与线性状态变量模型在分油活门位移、速度、控制腔压力及作动筒的速度、位移等方面的响应对比。提取的线性状态空间模型式（6）在全行程范围内与非线性模型完全一致，模型精度很高。

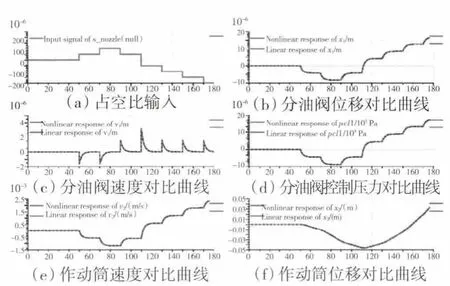
图11 喷口作动筒在行程内变化时状态变量变化曲线

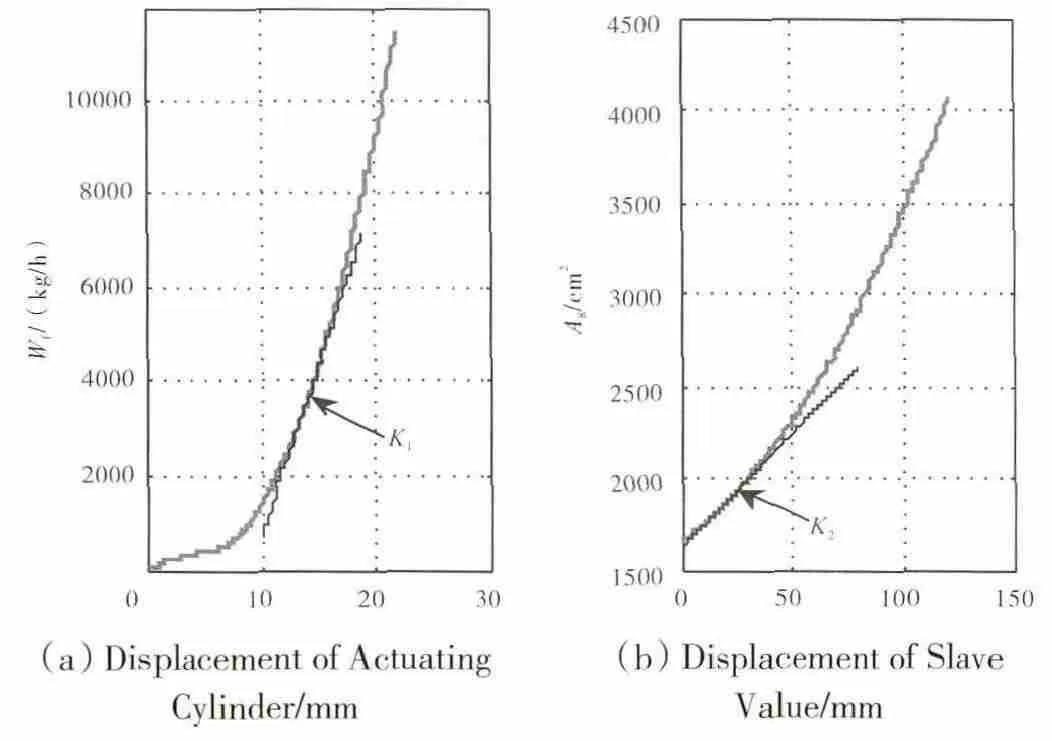
图12 主燃油量及喷口面积与活塞位移的关系

在图6、7、10、11中，主燃油计量执行机构和喷口调节机构的动态响应均为开环情况，因此动态响应时间较长。文中给出开环动态模型，目的是提供1个具有一般性的开环对象，有利于在本文研究基础上自行设计执行机构闭环控制器和发动机闭环控制器，进行执行机构的开环/闭环故障诊断。

3 增广发动机模型的验证与应用分析

由主燃油计量阀随动活塞位移与计量活门输出燃油量以及喷口面积作动器作动筒活塞位移与喷口面积为非线性关系如图12所示。从图中可见，变增益系数K1和K2为非线性曲线对应工作点处斜率，可用小偏差求导的方法求得。

在实际工程中，发动机在加减速大过渡态工作时将出现控制量的饱和，这种饱和效应将反映在执行机构的输出中。因此，为消除这种饱和效应，采用加减速控制器与主控制器输出低选的方式，并辅以执行机构的位置饱和与速率饱和限制的控制。带执行机构的发动机控制系统结构原理如图13所示，从图中可见，带灰色背景的点划线框内为带执行机构的增广发动机模型，即本文所完成的工作。其中，点线框左边的饱和环节为占空比信号本身的输入饱和特性（20%~80%），而这个输入限制直接导致了执行机构的速率饱和限制，ACT1和ACT2上的虚线箭头即为“导致”含义。在设计闭环控制器时，仅需要在ACT1和ACT2前加入占空比信号的输入饱和限制，速率限制即会自动出现，不需另外添加。点线框右侧的饱和环节为执行机构的位置饱和限制。点线框外侧表示在此增广模型的基础上可以开展的工作，包括执行机构小闭环的设计，带执行机构发动机大闭环多变量控制器设计等，以虚线框表示。仍取第2.1节中的稳态工作点为算例，其工作点参数为Wf=1.046kg/s，A8=1883cm2，该点处变增益系数K1和K2求解可得K1=717.6（kg/h）·mm-1，K2=12.32cm2/mm。

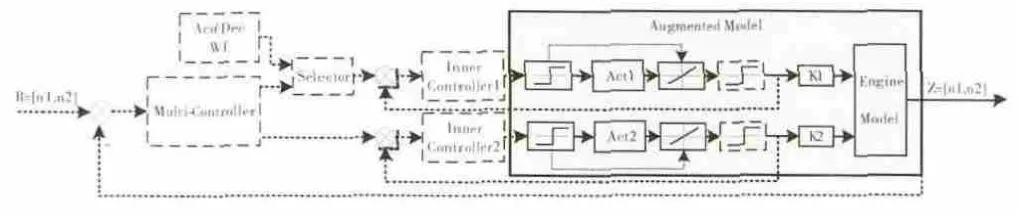
图13 带执行机构的发动机控制系统结构

从图6中可见，开环的主燃油调节执行机构本身是稳定的，当给定控制输入为阶跃信号时，可以得到稳定的计量活门位移，而确定的计量活门位移乘以该点处的增益系数K1即可得到稳定的燃油流量，因此控制输入SFuel给定为阶跃信号；从图10中可见，开环喷口执行机构是不稳定的，当给定控制输入为阶跃信号时，喷口作动筒的速度能达到稳定，而位移是速度的积分。因此为了保证喷口的截面积能进入稳定值，进而使发动机的输出能保持稳定，控制输入SNozzle给定为脉冲信号。控制输入阶跃信号SFuel和脉冲信号SNozzle如图14所示。用本文提出的差分进化算法提取包含发动机主要特征量及其执行机构状态变量的增广发动机状态变量模型输出响应与非线性模型输出响应对比曲线分别如图15、16所示。从图中可见，2种曲线具有较好的一致性。由于执行机构中往往只有线位移传感器LVDT和控制腔测压点，没有速度传感器，因此未加入对比。

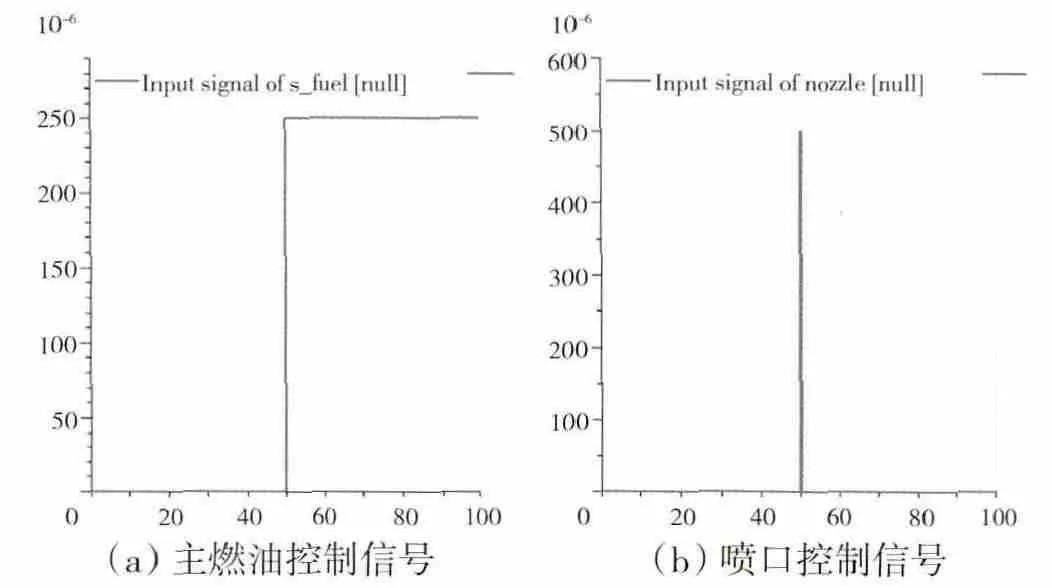
图14 控制输入阶跃信号SFuel和脉冲信号SNozzle

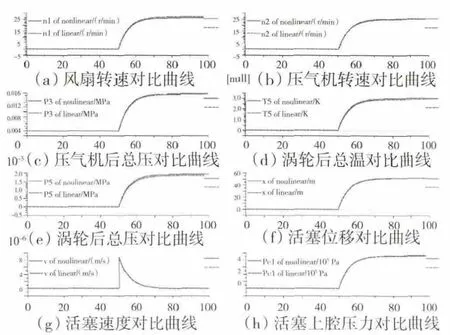
图15 SFule变化时的输出响应

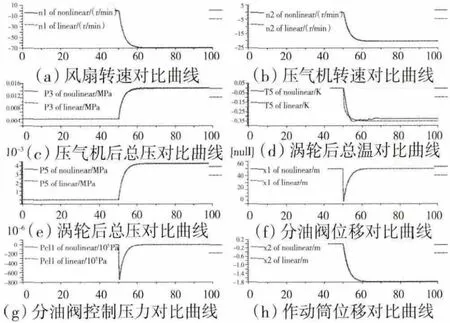
图16 SNozzle变化时的输出响应

4 结论

针对控制系统设计中往往忽略执行机构的问题，通过差分进化方法建立了包含执行机构和发动机模型的增广状态变量模型。通过与非线性模型的对比，表明该增广模型具有很高的精度。

该增广模型包含了执行机构的诸多状态变量，可以为故障诊断提供更多的信息便于故障的定位与隔离，以进行容错控制；考虑了执行机构对控制器输出能量的约束作用，因此针对该模型设计的控制器将具有实际工程价值；适用于执行机构小闭环控制器、带执行机构的发动机的大闭环控制器设计及带执行机构的故障诊断；便于实现过渡态与稳态的控制计划切换。

后续还将以该增广模型为基础，开展设计执行机构小闭环控制器及大闭环最优控制器研究。

[1]郑铁军，王曦，覃道亮，等.带执行机构的航空发动机控制系统设计仿真[J].推进技术，2005，26（4）：335-338.ZHENG Tiejun，WANG Xi，TAN Daoliang，et al.Design and simulation of control systems with actuators of aeroengine[J].Journal of Propulsion Technology，2005，26（4）：335-338.(in Chinese)

[2]Sugiyama N.Derivation of ABCD system matrices from nonlinear dynamic simulation of jet engine[R].AIAA-92-3391.

[3]Kulikov G G， Thompson H A.Dynamic modeling of gas turbines-identification，simulation，condition monitoring and optimal control[M].London：Springer-Verlag KG，2004：65-155.

[4]仇小杰.航空发动机多模态切换控制方法研究[D].南京：南京航空航天大学，2011.QIU Xiaojie.Muti-mode switching control for aircraft engines[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2011.(in Chinese)

[5]李秋红，孙健国.基于遗传算法的航空发动机状态变量模型建立方法[J].航空动力学报，2006，21（2）：427-431.LI Qiuhong，SUN Jiangguo.Aeroengine state variable modeling based on the genetic algorithm[J].Journal of Aerospace Power，2006，21（2）：427-431.(in Chinese)

[6]王斌，王曦，石玉麟，等.一种航空发动机分段实时线性动态模型[J].航空动力学报，2014，29（3）：697-701．WANG Bin，WANG Xi，SHI Yulin，et al.A real-time piecewise linear dynamic model of aeroengine[J].Journal of Aerospace Power，2014，29（3）：697-701.(in Chinese)

[7]Breikin T V，Arkov V Y，Kulikov G G.Regularization approach for real-time modeling of aero gas turbines[J].Control Engineering Practice，2004，12（4）：401-407.

[8]Storn R，Price K.Differential evolution a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkeley：International Computer Science Institute，1995.

[9]Giarre L，Bauso D，Falugi P，et al.LPV model identification for gain scheduling control an application to rotating stall and surge control problem[J].Control Engineering Practice，2006，14（4）：351-361.

[10]刘波，王凌，金以慧.差分进化算法研究进展[J].控制与决策，2007，22（7）：721-729.LIU Bo，WANG Ling，JIN Yihui.Advances in differential evolution[J].Control and Design，2007，22（7）：721-729.(in Chinese)

[11]刘金琨，沈晓蓉，赵龙.系统辨识理论及MATLAB仿真[M].北京：电子工业出版社，2003：233-254.LIU Jinkun，SHEN Xiaorong，ZHAO Long.System identification theory and MATLAB simulation [M].Beijing：Electronic Industry Press，2003：233-254.(in Chinese)

[12]Kaelo P，Ali M M．A numerical study of some modified differential evolution algorithms[J]．European Jof Operational Research.2006，169（3）：1176-1184．

[13]Wang SZ，Ma L X C，Sun D S.Hybrid differential evolution particle swarm optimization algorithm for reactive power optimization[C]//Chengdu：Asia-Pacific Power and Energy Engineering Conference(APPEEC)，2010.

[14]Manring N D.Hydraulic control systems[M].NewYork：John Wiley and Sons，2005：93-97.

[15]付永领，祁小野.LMS Imagine.Lab AMESim系统建模与仿真参考手册[M].北京：北京航空航天大学出版社，2011：1-97.FU Yongling，QI Xiaoye.LMS Imagine.Lab AMESim system modeling and simulation reference manual[M].Beijing：Beijing University of Aeronautics and Astronautics Press，2011：1-97.(in Chinese)

[16]赵连春，杰克·马丁利.飞机发动机控制-设计、系统分析和健康监视[M].北京：航空工业出版社，2011：17-21.ZHAO Lianchun，Mattingly J D.Aircraft engine controls：design，system analysis，and health monitoring[M].Beijing：Aviation Industry Press，2011：17-21.(in Chinese)