滚动轴承内圈故障的动力学模型建立及仿真

徐可君，任 帅，秦海勤，贾明明

（1.海军航空工程学院青岛校区，山东青岛266041；2.南昌航空大学测试与光电工程学院，南昌330063）

0 引言

滚动轴承是旋转机械中最常用也是最易损坏的部件之一，及时发现轴承早期故障，对预防事故的发生具有重要意义，因此有必要开展滚动轴承故障的动力学特性研究。

目前有关滚动轴承故障的分析更多是对整个转子系统的动力学分析，对局部损伤故障轴承的研究相对较少[1-4]。当滚动轴承存在单一点蚀故障时，故障区承载时会释放一定的变形而产生冲击振动，通过监测冲击振动的频率，即可判断故障是否存在[5-6]。基于该机理，研究人员建立了各种滚动轴承单一点蚀故障模型，例如东亚斌[7]假设滚动体滚过故障时突然释放压力，在离开故障时又瞬间恢复原受力状态；张亚洲[8]在Ho模型的基础上，引入滚动体的随机滑动和振动传递函数的影响；徐东[9]根据滚动体承受载荷的状况，引入分段函数来研究滚动轴承的故障。

本文在上述研究基础上，进一步考虑了滚动体通过故障时内圈释放变形量的影响，并基于接触变形量渐变释放的客观事实，通过将故障释放的接触变形量近似成1个线性函数，建立了滚动轴承内圈单一点蚀故障模型。该模型进一步真实揭示了内圈单一点蚀故障机理，解决了现有模型瞬间释放变形量导致冲击力和振动加速度过大的问题[10]，为滚动轴承状态监测和故障诊断提供了理论支持。

1 内圈单一点蚀故障的滚动轴承模型

在滚动轴承工作时，滚动体与滚道的接触可简化为用1组弹簧阻尼表示的模型。根据Hertz接触理论，在内外圈滚道接触角相等的情况下，滚动体与双侧滚道总的等效接触变形系数为[11]

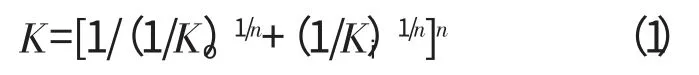
式中：Ko、Ki分别为滚动体与外、内圈的接触变形系数；对球轴承n=1.5，对圆柱滚子轴承，n≈1.11。

假设在内圈上某一点存在局部点蚀故障缺陷，其模型如图1所示。φspall为故障中心的初始位置角。考虑轴承间隙的影响，第j个滚动体与滚道总的接触变形量为

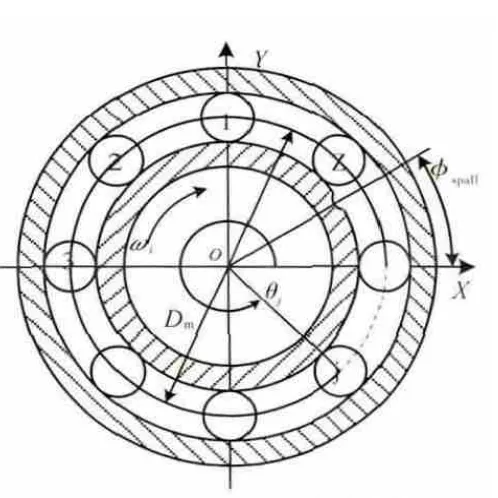
图1 内圈单点故障模型

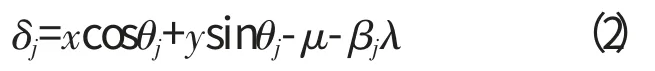
式中：j 为滚动体的序号；μ 为径向间隙；βj为开关量；λ 为滚动体滚过故障区释放的变形量；θj为第j个滚动体的位置角

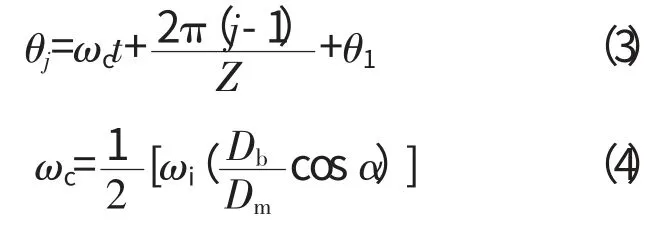
式中：ωc、ωi分别为保持架和内圈的旋转角速度；Z 为滚动体数目；θ1为1号滚动体的初始位置角；Db、α 为滚动体直径及其与滚道的接触角；Dm为节圆直径。根据图1中的几何关系，在内圈旋转过程中故障中心的位置角为

开关量βj表示滚动体是否与内圈缺陷相接触。当第j个滚动体的位置角θj处于故障中心的位置角之内时，则二者接触，存在接触释放变形量；反之亦然。因此βj可定义为

式中：Δφs为故障的跨度角。

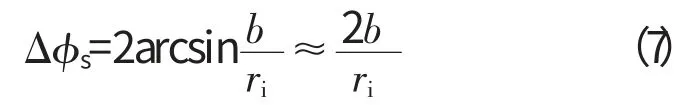
滚动轴承内圈局部点蚀故障如图2所示。从图中可见，故障宽度为2b，深度通常被定义为d'。由于实际的滚动轴承内圈不可能为完全意义上的刚性体，在与滚珠接触时，内圈本身也会变形。由于忽略了内圈的变形量，d'并不能完全表示内圈故障的严重程度。实际的故障深度应该是d'加上内圈的变形量Cdi，即如图2（b）所示的d。当滚动体通过内圈缺陷并且滚动体接触到缺陷底部时，释放的最大接触变形量λmax即为d；当滚动体通过内圈缺陷但并不能接触到缺陷底部时，释放的最大接触形变量λmax应该是滚动体的变形量Cdr和内圈的变形量Cdi之和，即

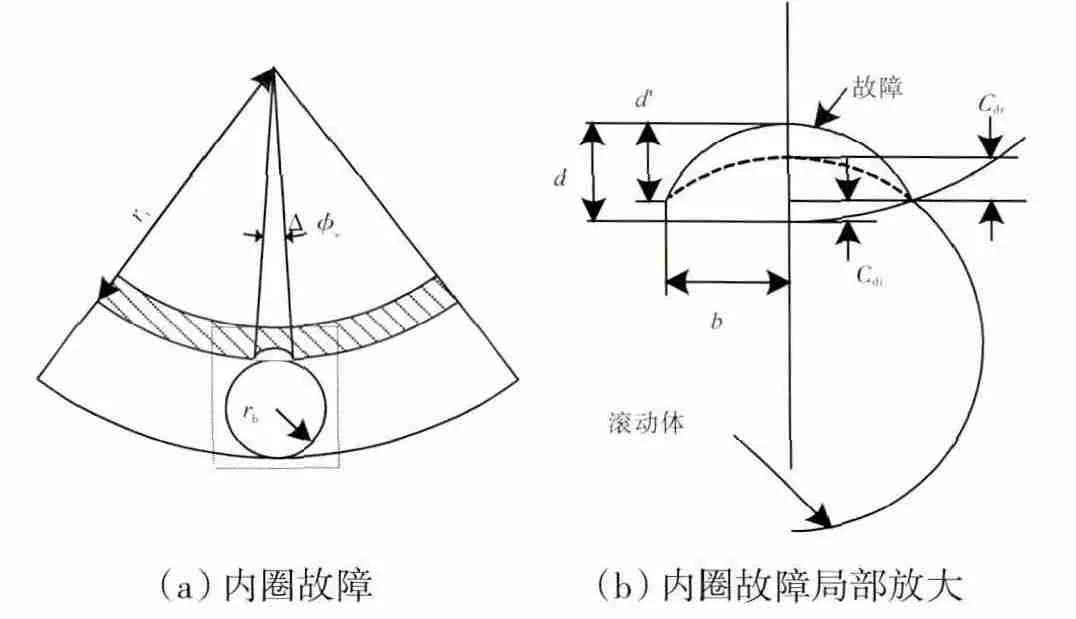
图2 内圈局部点蚀故障

由图2可得

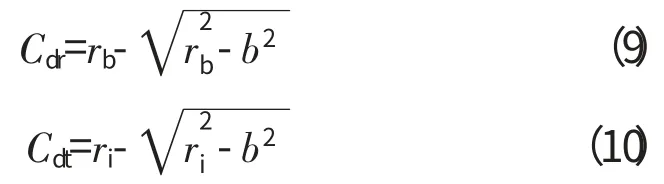
则滚动体通过内圈故障释放的最大变形量为

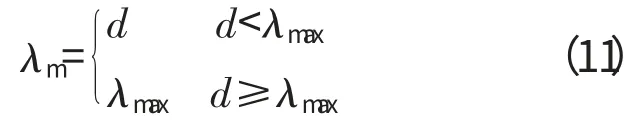
目前的内圈故障释放模型是如图3（a）所示的理想模型，即将点蚀缺陷理想化为矩形缺口，当滚动体一进入故障区就瞬间释放全部变形量，离开的瞬间又重新获得接触变形；而更多实际的点蚀缺陷如图3（b）所示的截面为一圆弧的缺口，变形的释放和重新获得是1个渐变的过程[10]。当在进入和离开缺陷的接触点A、C 点处时，|φs-θj|=Δφs/2，由故障释放的变形量为零；接触点靠近弧线最低点B 时变形量逐渐变大，并且在B 点|φs-θj|=0，释放的变形量达到最大。假设A、C 点相对于弧线最低点B 左右对称，由于实际的点蚀故障弧线长度相较于内圈半径很小，因此弧线AB 和BC 可近似当成直线。根据以上分析可知实际的释放形变量应该是在式（11）的基础上，考虑形变释放或重新获得的渐变过程所得

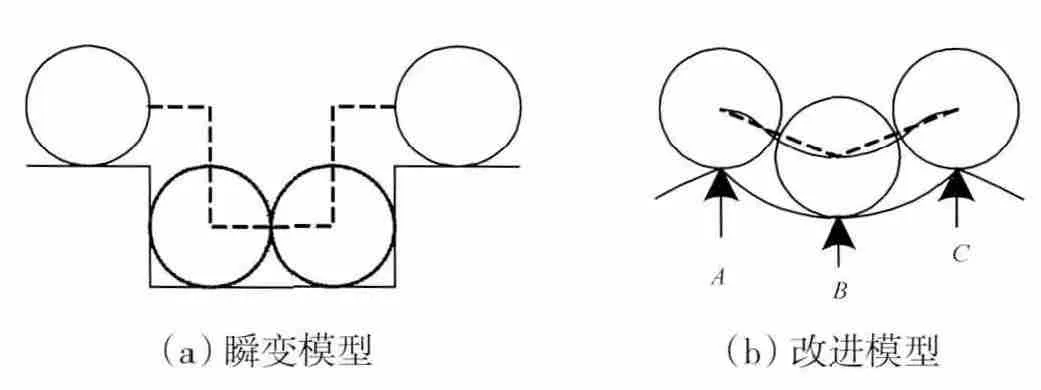
图3 内圈故障变形释放模型

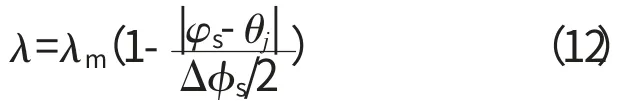
根据Hertz理论，第j个滚动体所承受的接触载荷为

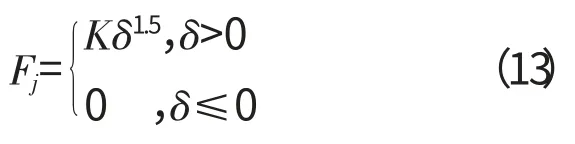
将Fj分别在X、Y 方向进行投影，可得单个滚动体对外圈的接触载荷为

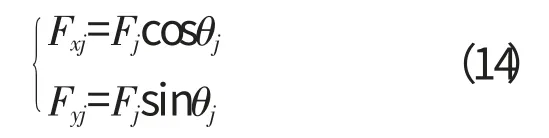
将所有滚动体的接触载荷相加，得到外圈在X、Y 方向总的接触载荷分别为

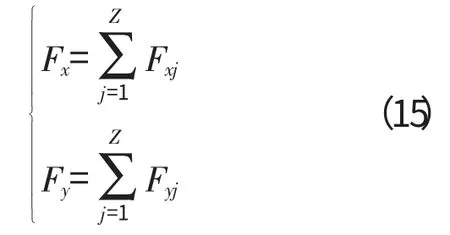
根据牛顿第2定律，滚动轴承外圈的非线性振动方程为

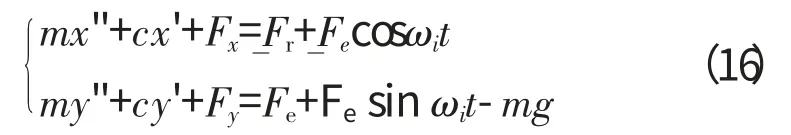
式中：m 为外圈质量；c 为系统的等效阻尼；Fe、Fr分别为转子偏心载荷和外加载荷。

2 含内圈单一点蚀故障的滚动轴承仿真与试验分析

2.1 仿真分析

以SKF6205型轴承为例，建立如式（16）的滚动轴承外圈的非线性振动方程。利用4阶5级龙格-库塔法求解该非线性方程。轴承的内、外径分别为25、52mm，最大壁厚为15mm，滚动体数为9，节径39.04 mm。假设故障深度为0.2mm，宽度为0.5mm，初始条件为x=y=0，x'=y'=0，初始、终止时间分别为0.2、0.3 s，等效阻尼c=200N·s/m，内圈转速n=1772r/min，偏心载荷，偏心距，外加载荷Fr=200N，滚动体通过内圈频率（即内圈故障特征频率）的理论值为159.93 Hz。内圈单点故障的振动速度加速度仿真曲线如图4所示。

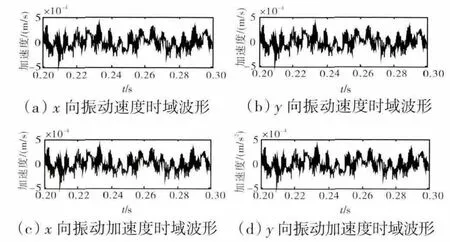
图4 内圈单点故障仿真结果

从图中可见，当滚动轴承内圈存在点蚀故障时，其速度信号在0.1s内约有16次冲击，特征频率约为160Hz，与滚动体通过内圈的频率相对应。由于受冲击载荷的作用，当滚动体通过故障缺陷时，导致振动加速度的响应量值明显大于振动速度的。

低频段的信号频谱如图5所示。从图中可见，速度和加速度信号频谱成分主要包括：内圈转动频率(29.3Hz)、滚动体通过内圈频率及其高次谐波(159.9、319.9Hz)以及内圈转频导致的边频(130.6、189.2Hz等)。而频率结构中高次谐波的出现可能主要是由式（13）的接触载荷与接触形变量之间的非线性关系所引起。振动速度信号的幅值为10-4m/s2量级，而振动加速度信号的幅值为10-1m/s2量级，并且在速度信号频谱结构中，滚动体通过内圈频率即内圈故障特征频率与转动频率的比值约为1.5，而相应加速信号频谱结构中对应的比值约为10，内圈故障特征频率及其倍频相对内圈转频的比值增大，有利于故障诊断。

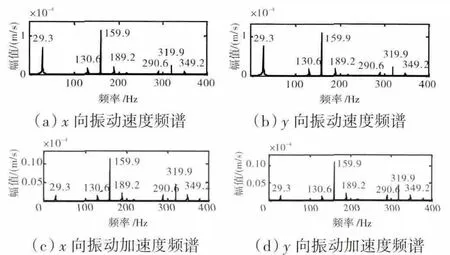
图5 内圈单点故障仿真频谱

2.2 试验分析

为验证该模型的准确性，采用美国西储大学标准轴承实验台的数据[12]，用电火花法在SKF6205型轴承内圈上加工1个深度为0.2mm，直径约0.53mm的点蚀故障。采样频率为48kHz，转速为1772r/min，其时域及低频段的波形如图6所示。

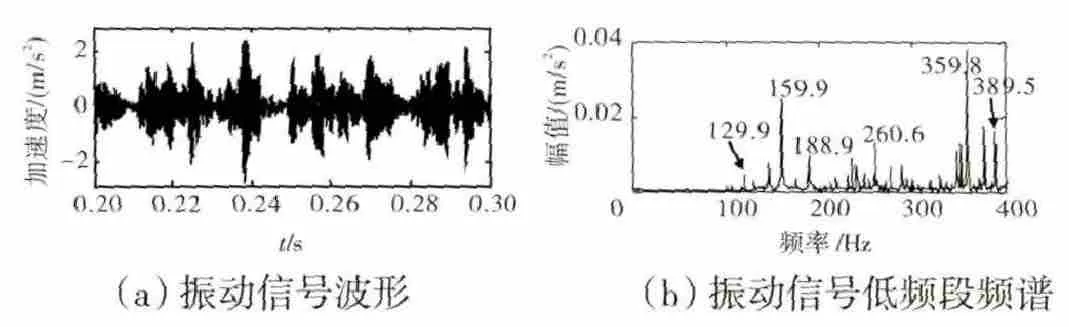
图6 内圈单一故障的试验结果

从图中可见，（a）时域波形很难得出任何故障信息，而（b）的频谱可以得出内圈故障特征频率（159.9 Hz）及内圈转动频率导致的边频（189.9Hz）、内圈转动频率的高次谐波（129.9、359.8、389.5Hz），与仿真信号的结果相一致。此外，还存在大量边频，应是由保持架转动频率、架相对内圈频率的调制作用以及背景噪声的干扰引起。另外，需指出的是由于受试验信号背景噪声的干扰，内圈转动频率（29.3Hz）被噪声所淹没，频谱结构中没有显现。

3 总结

基于Herz接触理论，建立了内圈单一点蚀故障的滚动轴承的动力学模型。模型考虑了内圈变形量的影响；同时基于变形量渐变释放的客观事实，给出了滚动体进入和离开故障区时释放形变量变化规律及计算方法，使模型更符合滚动轴承内圈故障的实际运行状态。通过仿真和试验，证明了该模型的正确性，为滚动轴承状态监测与故障诊断提供了理论支持。

[1]Harsha SP，Sandeep K，Prakash R.The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings[J].International Journal of Mechanical Sciences，2003（45）：725-740.

[2]Kankar P K，Harsha S P，Kumar P，et al.Fault diagnosis of a rotor bearing system using response surface method[J].European Journal of Mechanics A/Solids，2009（28）：841-857.

[3]李朝峰，孙伟，王得刚，等.两类转子－轴承系统模型非线性特性研究[J].中国机械工程，2009，20（2）：218-222.LI Chaofeng，SUN Wei，WANG Degang，et al.Study on nonlinear characteristics of two type rotor-bearing systems[J].China Mechanical Engineering，2009，20（2）：218-222.(in Chinese)

[4]曹登庆，杨洋，王德友，等.基于滞回碰摩力模型的转子系统碰摩托响应研究[J].航空发动机，2014，40（1）：1-9.CAO Dengqing，YANG Yang，WANG Deyou，et al.Study on rub responses of rotor systems based on hysteretic rub-impact force model[J].Aeroengine，2014，40（1）：1-9.(in Chinese)

[5]苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击，2010，29（3）：18-21.SU Wensheng，WANG Fengtao，ZHANG Zhixin，et al.Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J].Journal of Vibration and Shock，2010，29（3）：18-21.(in Chinese)

[6]韩磊，洪杰，王冬.基于小波包分析的航空发动机轴承故障诊断[J].推进技术，2009，30（3）：328-331.HAN Lei，HONG Jie，WANG Dong.Fault diagnosis of aero-engine bearings based on wavelet package analysis[J].Journal of Propulsion Technology，2009，30（3）：328-331.(in Chinese)

[7]东亚斌，廖明夫，张小龙.具有局部故障滚动轴承的振动分析(I)外圈具有单一局部故障[J].西安建筑科技大学学报，2012，44（1）：147-152.DONG Yabin，LIAO Mingfu，ZHANG Xiaolong.Virbration analysis of rolling elements bearing with localized defects（Part I-a single defect in outer race）[J].Journal of Xi’an University of Architecture and Technology，2012，44（1）：147-152.(in Chinese)

[8]张亚洲，石林锁.滚动轴承局部故障数学模型的建立与应用[J].振动与冲击，2010，29（4）：73-76.ZHANG Yazhou，SHI Linsuo.Establishment and application of mathematical models for rolling element bearings with localized faults[J].Journal of Vibration and Shock，2010，29（4）：73-76.(in Chinese)

[9]徐东，徐永成.单表面故障的滚动轴承系统非线性动力学研究[J].机械工程学报，2010，46（21）：61-68.XU Dong，XU Yongcheng.Research on nonlinear dynamics of a single surface defect in rolling element bearing systems[J].China Mechanical Engineering，2010，46（21）：61-68.(in Chinese)

[10]Sawalhi N，Randall R B.Simulating gear and bearing interactions in the presence of faults（Part I-the combined gear bearing dynamic model and the simulation of localized bearing faults[J].Mechanical Systems and Signal Processing，2008，22：1924-1951.

[11]邓四二，贾群义，王燕霜.滚动轴承设计原理[M].北京：中国标准出版社，2008：74-75.DEND Sier，JIA Qunyi，WANG Yanshuang.Design principles of roller bearing element[M].Beijing:：Standards Press of China，2008：74-75.(in Chinese)

[12]Ocak H，Loparo K A.HMM-based fault detection and diagnosis scheme for rolling element bearings[J].Journal of Vibration and Acoustics，2005，127：299-306.