PR状态方程在超临界喷射模型中的应用

范珍涔，范 玮，靳 乐

（1.中航工业燃气涡轮研究院，成都610500；2.西北工业大学动力与能源学院，西安710072）

0 引言

随着高超声速飞行器的发展，对高性能动力装置的需求越来越强烈。随着飞行速度的提高，发动机的工作参数将会发生一定改变，其燃烧室中燃烧的初始环境温度和压力有望超过航空煤油的临界值。另外，高超声速飞行器对冷却系统的要求不断提高，作为飞行器的惟一自带介质的燃油将作为首选的冷却介质，燃油在冷却机体和发动机热端部件的同时自身温度也被提升，逐渐达到并超过燃油的临界点温度。因此，未来高速飞行器动力装置的燃烧室中必定会出现超临界工况，而超临界喷射、蒸发和燃烧过程与常规亚临界工况差别极大。探索液态碳氢燃料的超临界喷射和燃烧机理成为高性能空天动力领域亟需解决的关键问题之一。

对超临界流体的基础研究表明[1]，当典型液态碳氢燃料——航空煤油处于超临界状态时，其既不属于液相也不属于气相，煤油的物性表现为既具有液态煤油的密度又具有气体的性质，具有等价的气相和液相密度值，兼具气体的低黏度和液体的高密度以及介于气体和液体之间的高扩散系数等特征，并且其物性参数随着温度和压力的改变而显得非常敏感。这些物性的特殊性是造成超临界喷射及其混合燃烧过程与亚临界情况下迥异的直接原因，国内外学者针对超临界碳氢燃料的喷射进行了相关研究并得到了一定成果。Newman[2]在1971年就考虑到未来先进发动机的发展趋势，率先对近临界热力学条件下的液态喷射进行了研究，发现了表面张力大大减小的现象，拉开了超临界喷射研究的帷幕；Mayer等[3]试验研究了液氮和液氮/氦气混合物喷射到氮气和气态氮/氦混合物超临界环境中的喷射过程；Wu等[4-5]对超临界乙烯喷射到静止的亚临界氮气环境中的现象，试验研究了临界点附近输运参数变化对激波结构的影响；Oscbwald[6]利用拉曼光谱法对超临界氮气自由喷射的试验研究发现，在临界点附近的喷射所吸收的热量不会提高流体的温度而使得喷射更为扩展，同时表面张力消失，喷射速度和动量对于喷射的影响很小，喷射的主要控制因素是环境的热力学参数；Chehroudi等[7]分别对亚临界流体喷射到超临界环境中喷射与可变密度的湍流气体喷射的喷射扩张角进行了对比试验研究，分析发现2种喷射在喷射扩张角上存在定量的相似；Barata等[8]利用可变密度喷射的数值模型对试验数据进行了验证计算，得到了较好的吻合；Sui等[9]在非常接近临界点的情况下进行了超临界SF6流体喷射到静止的N2和CO2高压环境的试验研究；Chen[10]研究发现超临界喷射的射流穿透长度的主要影响因素是喷射温度和腔室的压力；Douthip[11]通过试验和数值计算对比研究了超临界喷射长度和喷射扩张角随着喷射流量和温度的变化规律，并与相同流量和出口压力下的亚临界喷射进行了对比分析，发现超临界的喷射长度要小于亚临界的。上述研究中，绝大部分都以小分子、单组分的燃料为研究对象，使用实际液态碳氢燃料的极少。同时，大部分研究针对跨临界喷射，对于超临界流体喷射到超临界环境中的研究很少。

本文以液态碳氢燃料的超临界喷射为背景，考虑超临界流体物性的特殊性，对比PR方法与理想气体方法应用于超临界喷射的可行性，得出了能够较为准确模拟超临界喷射的数值模型。

1 PR状态方程及其热力学关系

在超临界喷射中应该考虑到实际气体效应，压缩因子z 的定义为

式中：T 和P 分别为温度和压力；Vm为摩尔体积；R 为气体常数。

对于理想气体来说z=1，而对于超临界流体来说，通常z<1。

Peng-Robinson[12]考虑到实际气体的效应，建立了2参数的状态方程，即

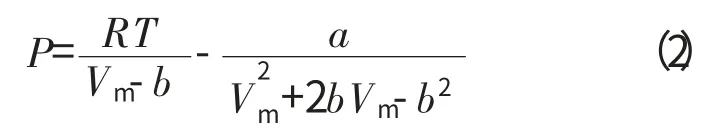
式中：参数a 和b 的值可以由物质的临界性质求得，其与临界压缩因子zc的具体取值见表1。

表1 PR状态方程中参数的取值

从表中可见，fω是1个关于偏心因子ω 的函数，可以由式（3）求出。Pc、Tc分别为物质的临界压力、临界温度。典型物质的临界状态参数见表2。从表中可见，一些典型物质的临界参数、压缩因子和偏心因子的值，大部分物质的实际临界压缩因子值与上述方法计算得到的值都非常接近。

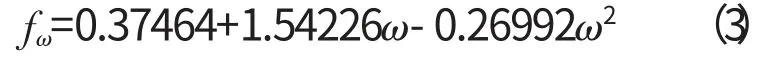
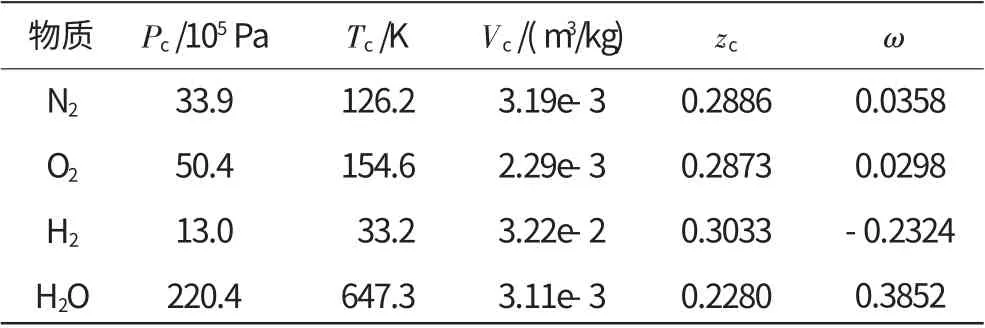
表2 典型物质的临界状态参数

进行超临界流体热力学参数的计算可以采用相对偏差法：选定参考状态，将热力学参数通过状态方程与P、V、T 相关联。各种热力学参数的解析表达形式为

式中：S 和H 分别为熵和焓；S0和H0分别为参考状态下的熵和焓值。

对于定压比热和定容比热，同样可以采用相对偏差法来求得。真实气体比热可以表示为

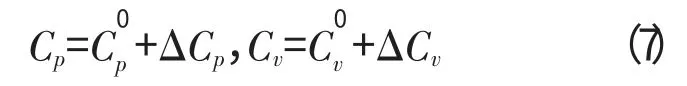
式中：ΔCp和ΔCv称为剩余比热容，表达式为

式（8）、（9）定义了真实气体比热和理想气体比热之间的关系，通过将PR状态方程代入上述公式中，即可以求出所有的热力学参数值。

2 数值模型的建立

2.1 物理模型

本文主要对航空煤油的常用替代燃料——C10H22（正癸烷）喷射到超临界N2环境的超临界喷射过程进行了数值模拟。计算的物理模型如图1所示。从图中可见，燃料进口直径为0.254mm，N2进口宽度为3.968mm，喷射腔室充满N2。具体边界和工况条件的设置与Douthip[11]的试验中的保持一致，见表3。

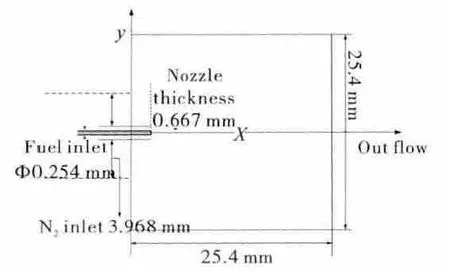
图1 物理模型

表3 数值计算模型的边界和工况条件参数

2.2 数值模型

将控制方程微分化之后，可以得到

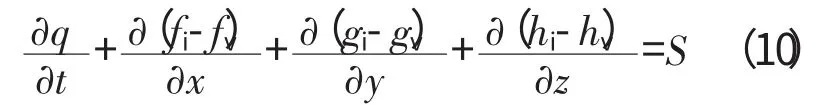
式中：q 向量为相关的独立守恒变量；f、g 和h 分别为在3个空间方向上的通量；S 为源项。下标i 和v 分别为无黏和黏性流动项。基于雷诺平均的Navier-Stokes方程，独立变量和无黏通量可以表示为

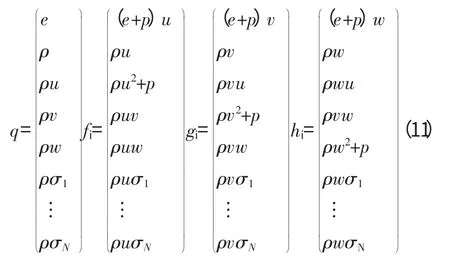
式中：e 为单位体积内的总能量；u、v 和w 分别为各方向的速度；σi为在湍流模型中的一些湍流传输特性，例如湍流动力学能等。

上述结构形式适用于多相流计算。式中前5 行表示标准的欧拉方程，分别为能量方程、连续方程和3个动量方程。将实际气体的状态方程（P=zρRT）用守恒变量表示为

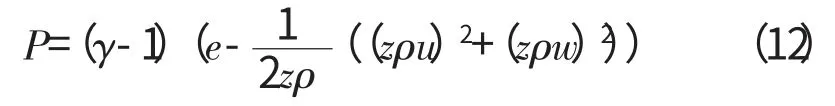
式中：γ 为比热比：z 可通过状态方程得出。黏性项定义为

式中：K 为热传导系数；D 为扩散系数；τij为黏性压力，定义为

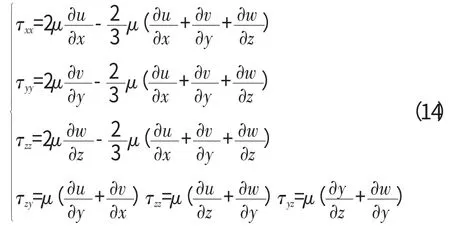
式（14）首先假定了斯托克斯法在气体计算中的正确性，因此衍生出第2黏性系数κ，其值为动力黏度μ 的2/3。

温度同样可以通过状态方程由守恒变量求出，即

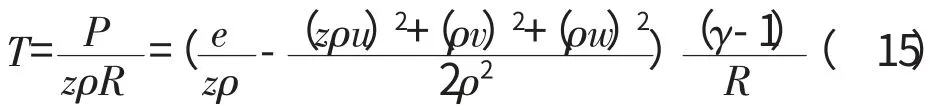
源项则可表示为

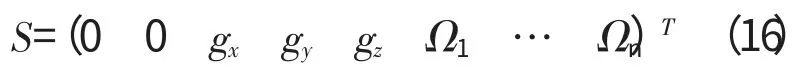
式中：gx、gy和gz为体作用力；Ωi为源项。

3 结果分析

利用上文的物理和数值模型对采用了PR状态方程的实际气体模型和理想气体模型进行了对比数值研究。2种模型对进口参数预测的相对误差（理想气体模型预测值－实际气体模型预测值）/ 理想气体模型预测值×100%）见表4。从表中可见，2种模型对氮气参数的预测差距很小，而对燃油参数的预测差距较大。

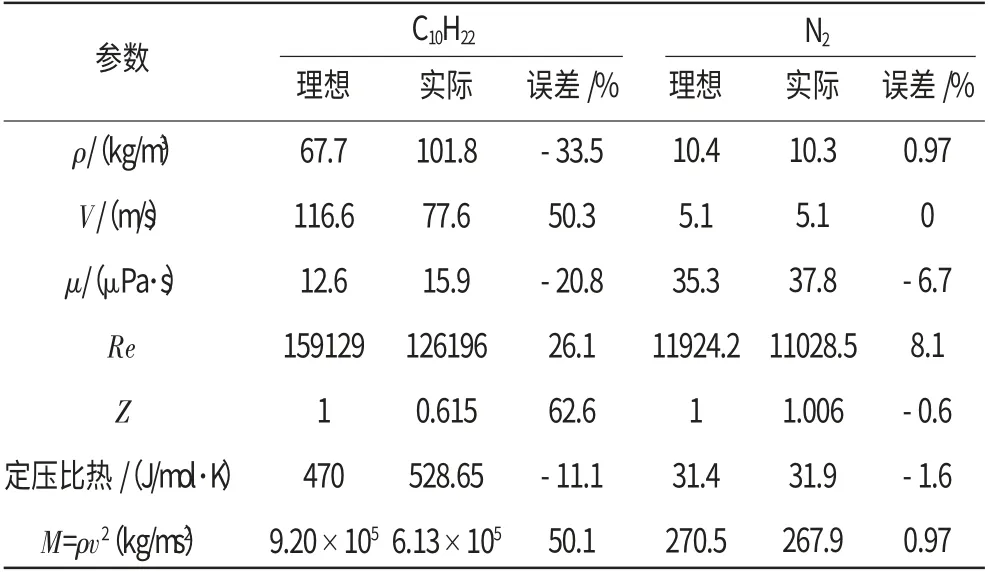
表4 2种计算模型对进口参数预测的相对差异

表中Re 的数值可根据式（17）由进口流速V、进口处动力黏度μ、密度ρ 和进口直径Dinj求出。

为了评估这种影响，基于数值计算结果，对2种模型所求得的喷射稳定后的各物性参数的分布进行了对比。

3.1 密度的分布

2种模型求得的喷射稳定后的密度分布和不同径向距离上密度沿轴向的分布情况分别如图2、3所示。图中，横坐标X/Dinj为轴向距离X 与喷嘴直径Dinj之间的比值，纵坐标Y/Dinj为径向距离Y 与喷嘴直径Dinj之间的比值。通过计算结果可知，图2中的实际气体模型模拟结果与文献[11]中的数值模拟和试验结果较为吻合，而理想气体模型模拟结果的误差很大。理想气体的密度预测偏低，速度预测值偏高，动量预测偏大。因此，造成密度较大的区域分布长度预测偏高。

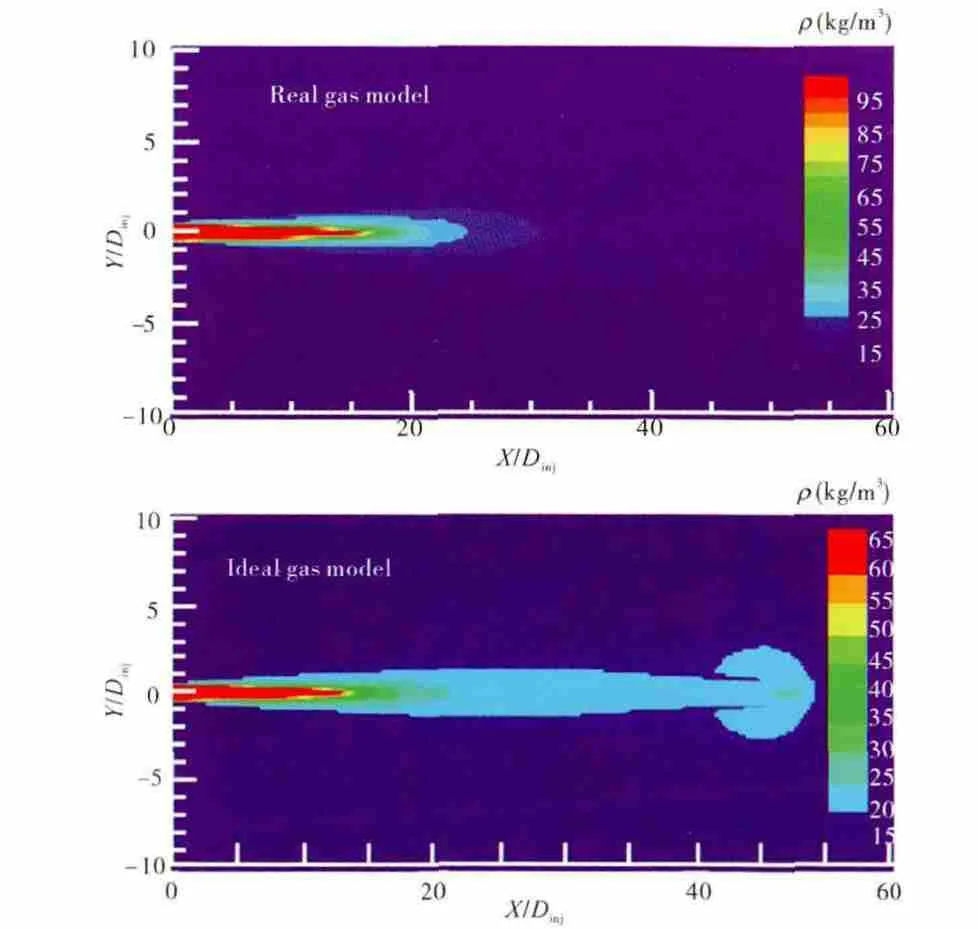
图2 2种模型求得的密度分布

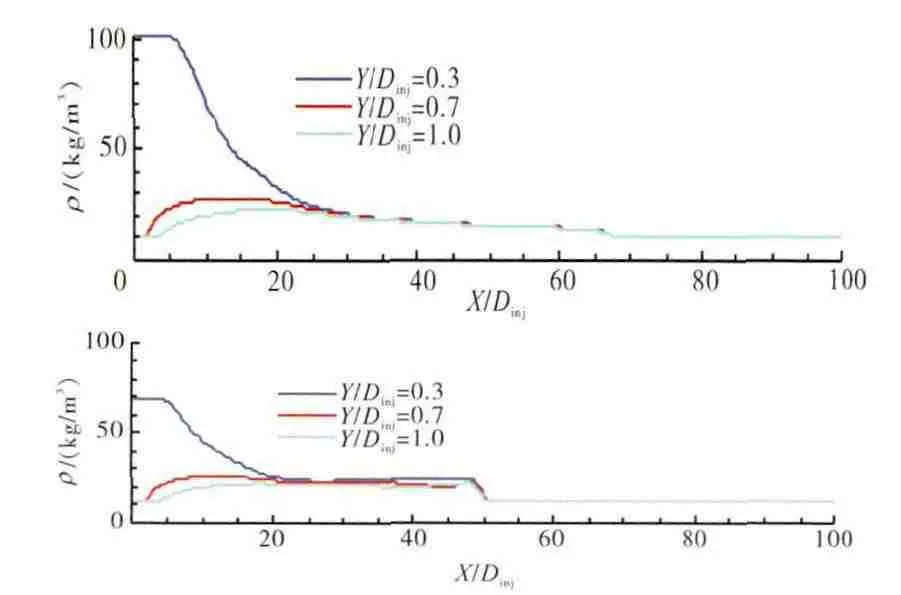
图3 不同径向位置的密度沿轴向的分布

从图3中可见，距离喷嘴中轴线越远的位置，2种模型的密度预测值越接近。越远离中轴线，氮气量越大，理想气体模型预测气态密度的准确性较高，因而越远离中轴线，理想气体模型密度预测越接近真实值。同时，在理想气体模型预测结果中，沿轴向方向，在X/Dinj=45～50处出现陡降，而在实际气体模型预测结果中，该现象发生于X/Dinj=60～70处。这是由于理想气体模型预测超临界燃油密度值偏低，与氮气的密度差距更小造成的。燃油和氮气密度差距越小，在混合过程中，在相同氮气质量分数下，混合体系密度越接近氮气，出现明显下降的位置越靠前。

3.2 温度

2种模型求得的喷射稳定后的温度分布如图4所示。从图中可见，由实际气体模型求出的温度分布场在轴向温度逐渐升高，在X/Dinj≈65时与环境气体的温度一致，而由理想气体模型求出的温度分布场则在轴向在计算域内一直未能与环境气体的温度一致。

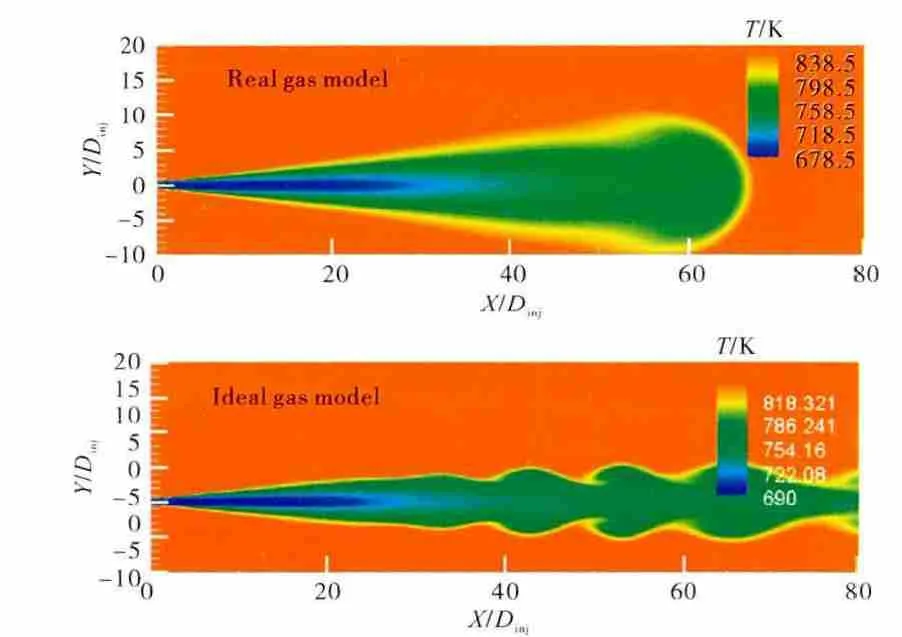
图4 2种模型求得的温度分布

由于理想气体的定压比热在温度较高的情况下，预测值比实际气体的大得多，偏离真实情况量太大，因此升温过程的模拟变得很缓慢，造成了图中这种明显的区别。从图中还可见，在喷射温度较低的核心区域长度内，理想气体模拟得到的结果比实际气体模拟得到的结果要低一些，这同样是由比热预测的差异造成的，在温度较低时，采用理想气体方法求出的比热值比实际情况的低，造成升温过程较快，低温核心区域长度预测偏小。2种模型求得的燃油和环境的交界面情况有所不同，由理想气体模型求得的温度分布云图出现了湍流特征，这是由于理想气体模型求得的喷射雷诺数过大所造成的。

不同径向位置上的温度沿轴向的分布如图5所示。从图中可见，在燃油温度较低的情况下（X/Dinj<40），理想气体模型求得的温度随轴向距离的增大变化相对剧烈；而在燃油温度较高的情况下（X/Dinj>40），理想气体求得的温度随轴向距离增大的变化相对缓慢。这同样是由于理想气体热力学参数预测的巨大误差造成的，在燃油温度较低的情况下，理想气体模型预测的定压比热比实际值低，而在燃油温度较高的情况下，理想气体模型预测的定压比热比实际值高。

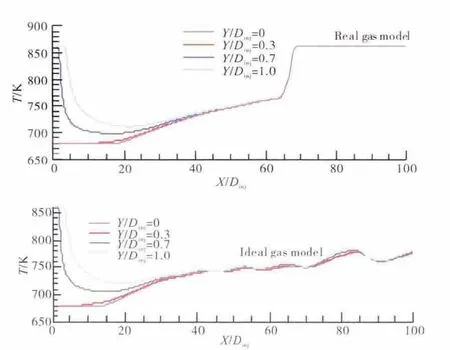
图5 不同径向位置上的温度沿轴向的分布

3.3 质量分数分布的预测

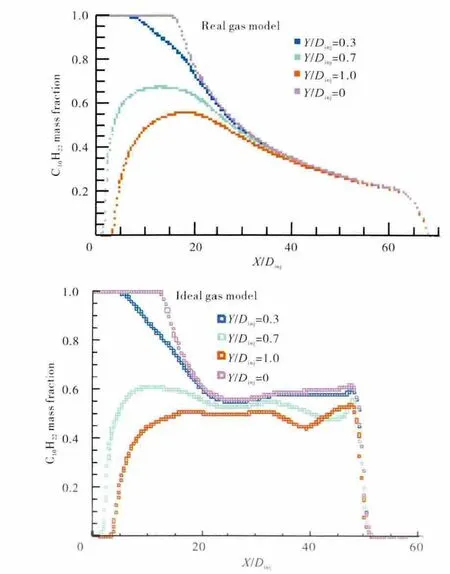
图6 不同轴向位置上的燃油质量分数沿轴向的分布

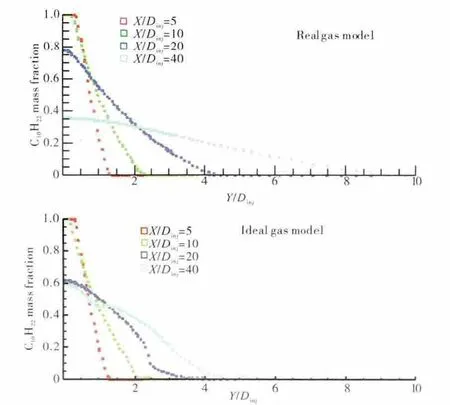
图7 不同径向位置上的燃油质量分数沿径向的分布

不同轴向和径向位置上燃油质量分数的分布分别如图6、7所示。从图6中可见，理想气体模型计算得出的燃油质量分数减小为零的轴向位置大概在X/Dinj=50处，而实际气体模型得出的则约在X/Dinj=70处。这说明理想气体模型得出的燃油轴向扩散区比实际气体模型模拟得出的低很多，这是由于理想气体模型只适用于中低压条件下的流体喷射扩散过程的模拟，且由于理想气体模型在预测密度、温度等物理量时均有一定误差，而这些物理量都是影响扩散过程的重要因素。同样，图7中的沿径向燃油质量分数的分布预测的差异也是上述原因造成的。

3.4 喷射长度和喷射扩张角的预测

喷射长度和喷射扩张角的计算方法与文献[11]中一致，即：喷射长度定义为喷射稳定后喷嘴出口到中心轴线上C10H22质量分数为0.2位置的距离；喷射扩张角定义为喷嘴出口处密度明显分界面的切线夹角。2 种不同模型计算得出的喷射长度和喷射扩张角的结果分别如图8、9所示。计算结果与Doungthip试验值[11]的对比见表5。

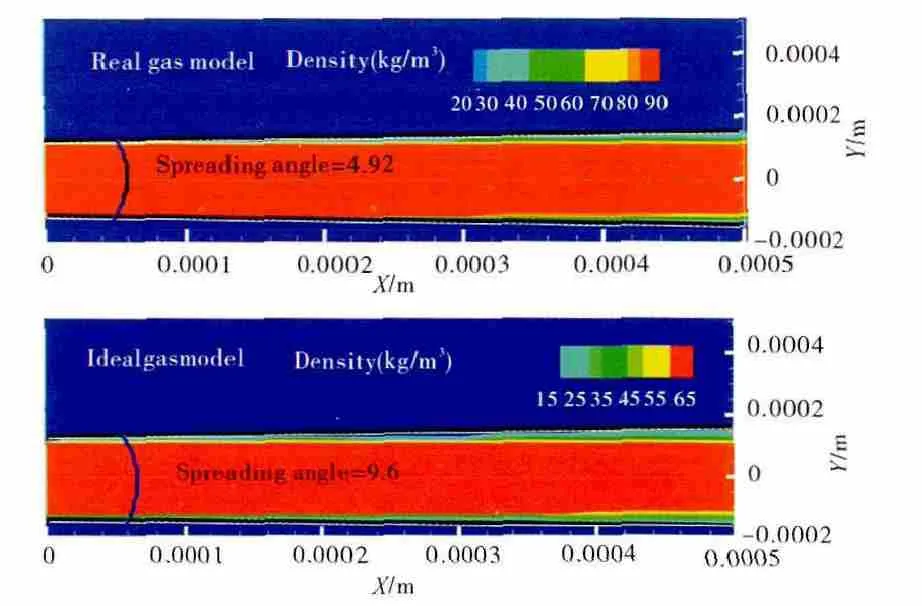
图9 2种模型对喷射扩张角的计算结果

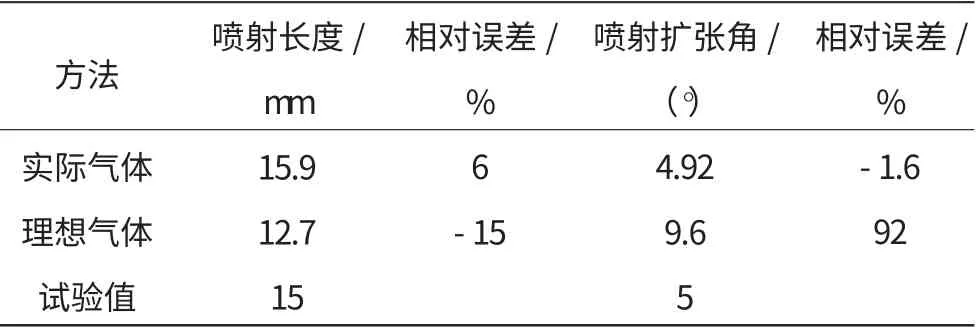
表5 喷射长度和扩张角计算值与试验值的对比

从表中可见，采用实际气体模型能够较为精确地预测出喷射长度和扩张角的值，而采用理想气体方法得到的结果与实际情况偏差非常大。这是由于喷射长度和扩张角的定义是基于密度或者质量分数的，而理想气体模型预测密度和质量分数都有较大误差，从而造成预测喷射特性产生巨大误差。

4 结论

以未来高性能航空发动机燃烧室中可能出现的超临界工况为研究背景，基于PR状态方程法，建立了考虑超临界喷射物性特点的数值计算模型。并将该计算模型与基于理想气体的计算模型进行了对比研究，分别得到了不同喷射模型的密度、温度、质量分数分布以及超临界喷射长度和扩张角的变化规律和差异性。通过与已有的试验结果对比，验证了基于PR方法模型的有效性和可靠性。该数值模型的建立和验证将为研究碳氢燃料的超临界喷射现象提供1种有效的数值工具。

[1]Holland M，Eaton E，Hanley H.A correlation of the viscosity and thermal conductivity data of gaseous and liquid ethylene[J].Journal of Physical and Chemical Reference Data，1983，12（4）：917-932.

[2]Newman J，Brzustowski T.Behavior of a liquid jet near the thermodynamic critical region[J].AIAA Journal，1971，9（8）：1595-1602.

[3]Mayer W，Schik A，Vielle B，et al.Atomization and breakup of cryogenic propellants under high-pressure subcritical and supercritical conditions [J].Journal of Propulsion and Power，1998，14（5）：835-842.

[4]Wu P，Chen T，Abdollah S，et al.Injection of supercritical ethylene in Nitrogen[J].Journal of Propulsion and Power，2006，22（4）：809-819.

[5]Wu P，Shahnam M，Kirkendall K，et al.Expansion and mixing processes of under expanded supercritical fuel jets injection into superheated conditions[R].AIAA-97-2852.

[6]Oscbwald M，Schik A.Supercritical Nitrogen free jet investigation by spontaneous Raman scattering [J].Experiments in Fluids，1999，27（6）：497-506.

[7]Chehroudi B，Talley D，Coy E.Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures[J].Physical Fluids，2002，14（2）：850-861.

[8]Barata J，Gokalp I，Silva A.Numerical study of cryogenic jets under supercritical conditions[J].Journal of Propulsion and Power，2003，19（1）：142-147.

[9]Chen L，Sui P.Atomization during the injection of supercritical fluid into high-pressure environment[C]//International Union of Theoretical and Applied Mechanics(IUTAM)Symposia on Droplets and Sprays，Taiwan：Springer，1994：6-10.

[10]Chen L.Heat transfer，fouling and combustion of supercritical fuels[R].AFOSR-TR-940321，1994.

[11]Douthip T，Ervin J，Williams T，et al.Studies of injection of jet fuel at supercritical conditions [J].Industrial and Engineering Chemistry Research，2002，41（23）：5856-5866.

[12]Peng D Y，Robinson D B.A new two-constant equation of state[J].Industrial and Engineering Chemistry Research Fundamentals，1976，15（1）：59-64.