基于Hadoop的不确定异常时间序列检测*

李 斌，张建平，刘学军

（南京工业大学计算机科学与技术学院，南京 211800）

基于Hadoop的不确定异常时间序列检测*

李 斌*，张建平，刘学军

（南京工业大学计算机科学与技术学院，南京 211800）

无线传感器网络中，传感器的采集与无线网络的传输等均可能带来时间序列的不确定性，而大数据时代的到来使得传统不确定异常时间序列检测研究面临时间效率低下的问题，为此提出基于Hadoop的不确定异常时间序列检测算法。首先对不确定时间序列进行压缩变换，使不确定数据量大大减少，然后利用MapReduce架构调用基于期望距离的不确定时间序列下的DTW算法，实现算法的并行化处理，降低算法时间复杂度。同时针对Hadoop集群任务级调度分配方法在运行中负载分配不均现象，提出Hadoop集群优化方法，明显缩减集群总任务时间，使得节点资源的利用更为合理。Hadoop平台下实验结果验证显示，该方法既提高了检测速度，又保证了检测准确率。

无线传感器网络；不确定异常时间序列；Hadoop集群优化；压缩；动态时间弯曲；期望距离

上世纪90年代开始，异常时间序列的检测搜索开始被广泛研究，而随着科学技术的发展，这一问题的研究越来越为人们所关注，它广泛应用于各个邻域，如传感器网络监控、运动物体追踪以及股票数据分析等。然而，现今大部分对异常时间序列的研究仅仅停留在确定性时间序列的研究上，但现实生活中，对移动对象的处理等产生的不确定性时间数据越来越多［1-2］。例如，在无线传感器网络中，无线传感器网络设备产生的数据天生就带有不确定性，网络传输过程中由于丢包等原因导致接收到的数据往往也是不确定的。而传统的异常时间序列检测算法并不能直接应用于不确定数据上，因此对传统算法的改进以及对新的适用算法的提出迫在眉睫。同时，不确定时间序列通常都具备长度长、数据量大的特点，大数据下的不确定异常时间序列检测研究显得尤为重要。因此本文提出一种基于Hadoop的不确定异常时间序列检测算法，采用Hadoop框架对海量时间序列进行并行化处理，提高检测速度的同时确保检测的准确度。同时对不确定时间序列进行压缩预处理，并对预处理结果提出基于期望距离的不确定时间序列的距离度量UDTW，进一步降低异常检测的算法复杂度。此外，针对Hadoop集群任务级调度分配方法在运行中负载分配不均现象，本文还提出Hadoop集群优化方法，缩减集群总任务时间，使得节点资源的利用更为合理。

本文后续内容安排如下：第1节介绍了相关研究工作；第2节提出了一种基于Hadoop的不确定异常时间序列检测算法；第3节通过相关实验分析了该算法的性能；第4节总结了全文的工作，并进行了展望。

1 相关工作

时间序列可以视为一个多维空间点，每个维度表示一个时间瞬间［3］。异常时间序列，通常被简单描述为传感器等采集到的时间序列中与正常序列有较明显差异的时间序列［4］。在之前的研究中，绝大数研究仍集中在确定时间序列上。通常确定时间序列为一条由确定的n维点组成的序列，相应地，不确定时间序列则是一条不确定的n维点序列，如图1所示。而随着科技的发展，在实际应用中，数据的各种不确定性使得不确定数据越来越多，这些不确定数据产生了大量的不确定时间序列，而时间序列中，异常时间序列的检测在序列的挖掘中又有着不可或缺的显著地位。Johannes Aßfalg等［5］于2009年首次提出一种概率性边界范围查询（PBRQ）方法，定义两条不确定时间序列之间的距离不确定，分别给定距离阈值α、概率阈值λ，认为若待检测不确定时间序列W与标准时间序列S之间的距离小于阈值α的概率大于等于阈值λ，即

PBRQα,λ（W,DB）=｛W∈DB|Pr（DIST（W,S）≤α）≥λ｝则待检测时间序列与标准时间序列相似，否则为异常时间序列。该方法准确地定义了不确定异常时间序列的检测方法，但由于两条不确定时间序列的距离是由大量可能的距离组成，因此，时间复杂度相对很高。Yuchen Zhao等［6］提出了不确定时间序列的小波分解构造方法，针对不确定数据集占用大量存储空间的问题提出Haar小波分解方法，将不确定数据进行压缩变换，同时采用两种不同的模式优化不确定性，此方法提高了查询效率，但并没有给出具体的不确定异常序列检测方法。吴红华、刘国华等［7］在Haar小波对数据压缩变换的基础上，对得到的不确定性时间序列概率维作纵向处理，提出一种选代表方法，采用概率最大法、均值法等选出一条确定的时间序列，并进行降维、索引，根据查询序列和数据库中的时间序列各自的不确定性进行组合，分别提出对应组合的相似性匹配算法，但该算法并未考虑海量数据下时间复杂度高的问题，因此有待完善。

图1 不确定时间序列

基于以上研究，本文提出一种基于Hadoop的不确定异常时间序列检测算法，构建Hadoop集群，运用MapReduce算法对时间序列进行分布式运算，降低算法的运行时间，使得大数据下的异常时间序列检测变得高效。同时对不确定时间序列进行压缩处理，使原始的不确定性数据量大大减少，降低存储空间。并对预处理得到的不确定时间序列采用基于期望距离的不确定时间序列的距离度量UDTW，计算不确定时间序列的DTW距离，从而简化不确定时间序列的建模，进一步降低存储代价。此外，针对当前Hadoop集群固有的任务级调度分配方法在运行中负载分配不均现象，采用基于节点能力的任务自适应调度分配方法对集群进行优化，使得集群总任务时间明显缩减，各节点负载更加均衡，节点资源的利用更为合理。

2 相关定义及算法描述

2.1 不确定时间序列压缩法（EDC）概述

通常时间序列为确定的n维点序列，而不确定时间序列在每个时间点上的取值是不确定的，这些数据点的可能取值由一系列取样点组成，每个取样点以一定的概率出现或服从某种分布，因此每个时间点上的取值用一个随机变量表示，不确定时间序列被认为是具有时间特性的随机变量的有序序列。

定义1（不确定时间序列）已知不确定时间序列XU，时间长度为n，每个时刻的样本观察值个数为s，则不确定时间序列可表示为：

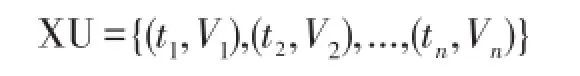
其中，ti为第i个时刻，Vi为第i个时刻观察值的集合，记为Vi=｛Vi,1,Vi,2,...,Vi,s｝。

由于不确定时间序列每个时刻可能值较多，往往数据量很大，因此时间序列的有效压缩对后续时间序列的深入计算与分析必不可少。本文提出不确定时间序列压缩表示方法，对不确定时间序列每个时刻的可能观察值，采用均值等表示形式对样本观察值进行压缩表示，避免直接存储不确定时间序列的所有可能值。

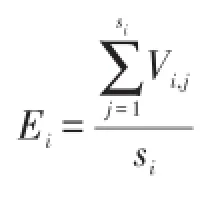
用四元组代替原始数据，得到不确定时间序列的压缩表示法，减少了数据量并降低了存储空间。同时由于本文后续不确定时间序列的DTW距离计算中涉及每个时刻样本观察值均值、方差计算，此种压缩方法也为DTW距离计算提供了计算基础，减少了算法的整体计算量。此外，若每个时刻的可能观察值增多，原有的四元组仍能有效表示可能值增多下的不确定时间序列，避免重复计算，降低计算成本。例1展示了这一过程。

例1 已知不确定时间序列XU，由n个形如（ti,si,Ei,Di）的四元组压缩表示，t1时刻样本观察值为a1,a2,......,as1共s1个，样本观察值均值为E1，样本观察值平方和为D1，若此时t1时刻样本观察值个数增加为s1+1，新增观察值为as1+1，则样本观察值均值为

值增加时，不确定时间序列可由原始四元组压缩表示方法线性计算得出。

2.2 不确定时间序列的DTW距离计算（UDTW）

从概率角度，不确定数据通常被认为是一个随机变量，因此不确定数据X、Y之间的距离为随机变量X、Y上的某个函数，因此，利用随机变量X、Y的距离函数定义的随机变量Z的期望来度量X、Y之间的距离是一种自然的想法［8］。

定理1 给定两个相互独立的不确定数据X、Y，且度量方式为欧式度量，则X、Y之间的期望距离为：ED（X,Y）=（E（X）-E（Y）2+D（X）+D（Y）。其中，E（X）为X的期望，D（X）为X的方差。

证明：

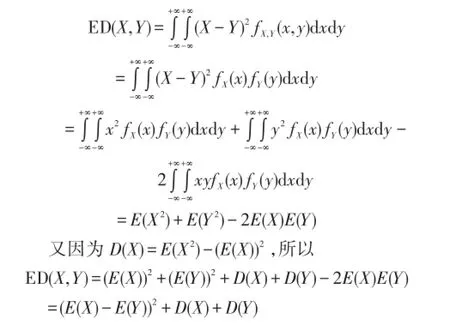
定义3 给定不确定时间序列X、Y，则最优动态时间弯曲距离UDTW＜i,j＞如下：

2.3 基于Hadoop的不确定异常时间序列检测算法（HUDTW）

2.3.1 Hadoop简介及Hadoop集群优化

Hadoop起源于Nutch项目，是Google公司的分布式文件系统GFS（Google File System）和MapReduce计算模型的开源实现。Hadoop的核心是MapReduce计算框架，是一种并行编程模型和计算框架，用于并行计算大规模数据集，因此在处理海量数据上卓有成效［9］［10］。

Hadoop框架中，每个作业被分割成等大小任务块传送至不同节点，所有任务完成才标志着作业的完成［11］。MapReduce的工作框架由一个主节点和多个从节点组成，JobTracker运行在主节点上，Task-Tracker运行于从节点。JobTracker将作业分成Map任务与Reduce任务，当TaskTracker发出请求时，JobTracker分配任务给从节点执行。由于JobTracker监听到任务请求后就会分配相应的任务，不管节点处理能力的高低，因此会出现：弱节点负载过重、剩余任务分配不合理、优势节点资源浪费等情况［12］。为避免此现象发生，本文以节点当前的负载状态作为参考标准，评价节点计算资源的利用程度，节点根据评价值再对运行任务的数量进行调整，达到集群优化的效果。节点的权值代表节点处理任务的能力，本文定义的节点权值与以下三个方面有关：节点性能、任务特征、节点失效率。

定义4

①若Hadoop集群中有n个节点，每个节点的节点性能为N，任务特征为T，节点失效率为F［13］，则节点i的权值为：②若Hadoop集群中有n个节点，节点i的权值为Wi，所有节点中最大权值为Wmax，则节点的权值比例参数为：

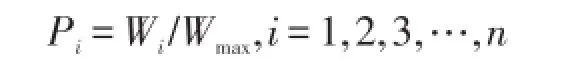
集群优化主要分为两部分：一、JobTracker端任务分配，二、TaskTracker端的自适应调节。当Tasktracker请求分配任务时，将该节点的权值比例参数Pi传递给JobTracker，JobTracker根据该节点的空闲slot数numslot及权值比例参数给该节点分配基本任务数（也称最小任务数）numtask，式（2）可计算基本任务数：

TaskTracker获取基本任务后，会存在剩余的slot槽，若剩余槽数大于节点第一次分配任务后的剩余槽数，节点继续请求分配任务，否则由目前节点负载状态决定是否继续申请任务。

定义5 若周期读取TaskTracker节点的CPU利用率、内存使用率、网络利用率分别为Ucpu、 Umem、Unet，且CPU、内存和网络带宽在当前节点负载中所占的比重分别为 fcpu、fmem、fnet，则节点负载状态为：

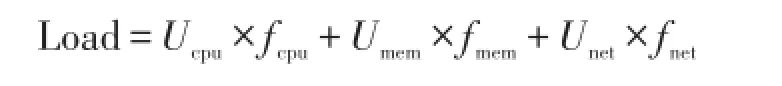
比较负载状态Load与节点负载阈值Threshold，若Load＜Threshold，继续分配任务，否则停止申请。2.3.2 基于Hadoop的不确定异常时间序列检测算

法（HUDTW）

由于不确定时间序列的可能世界较多，因此不确定时间序列数据量相对确定时间序列要大的多，而随着大数据时代的到来，传统检测算法已无法保证时间上的高效性，因此本文提出了基于Hadoop的不确定异常时间序列检测算法，采用分布式计算方法降低检测时间，提高检测效率。给定标准不确定时间序列与待检测不确定时间序列，则判断待检测不确定时间序列是否为异常时间序列首先要将时间序列进行分段处理，并整合形成文件上传至hdfs文件系统，然后进行MapReduce并行运算，最终输出结果。算法详细步骤如下：

输入：采集到的标准不确定时间序列A，待检测不确定时间序列B1，B2，…，Bm

输出：异常时间序列标志flag

Step 1 对所有不确定时间序列进行EDC压缩处理。

Step 2 将标准不确定时间序列A按时间间隔t分成n份，并处理为series=＜s，s_in，v＞的形式。其中s为时间序列A标记，记为0；s_in为时间序列时间段标记，（t，2t），…，（n-1）t，nt）依次记为t1至tn；v为上述标记下的时间序列内容。

Step 3 同理将m条待检测时间序列（B1，B2，…，Bm）依次按时间间隔t分成n份，处理为Pseries=＜Ps，Ps_in，Pv＞的形式.其中Ps为时间序列标记，B1～Bm依次记为1～m；Ps_in为时间序列时间段标记，m条待检测时间序列的时间间隔（t，2t），…，（n-1）t，nt）全部依次记为t1至tn；Pv为上述标记下的时间序列内容。

Step 4 将s_in值与Ps_in值相同的记录合并成一条记录，多条记录形成的数据文件上传至hdfs，执行MapReduce函数，函数由三个部分组成：Map函数、Combine函数、Reduce函数。

①Map函数

方法：对当前时间段的标准不确定时间序列与m条待检测不确定时间序列根据2.3.2节算法分别进行DTW距离的计算

输出：k2,v2。k2为待检测时间序列标记，v2为两时间序列之间的DTW距离。

②Combine函数

输入：k2,list（v2）。k2为待检测时间序列标记，list（v2）是分配给标记k2的两时间序列DTW距离组成的链表

方法：将属于同一标记的DTW距离进行相加运算

输出：k2,vl2。k2为Combine函数的输入，vl2为本地节点属于k2的不确定时间序列的DTW距离和。

③Reduce函数

输入：k2,list（vl2）。k2为combine函数时间序列标记，list（vl2）为各个combine函数输出的中间结果组成的链表，

方法：将不同节点的相同k2值对应的vl2值累加，定义参数 flag，将累加值与给定阈值ε比较，若累加值小于阈值，则k2值所代表的时间序列与标准时间序列相似，flag值为0；否则为离群时间序列，flag值为1。

输出：k3,v3。k3为Reduce函数的输入值，v3为 flag值。

Step 5 对于Reduce函数的输出k3,v3，若v3值为1，则此时间序列为离群时间序列，否则为非离群序列。

3 算法实验分析

本文实验部分采用10台双核计算机组建的Hadoop集群对不确定时间序列进行分析，操作系统为centos 6。其中一台作为namenode，一台作为secondarynamenode，其余8台均作为datanode。每个节点Map的数量为8个，Reduce的数量为1个。实验首先采用默认Hadoop集群从算法的时间复杂度和准确性两方面讨论算法的有效性。进行对比的算法为面向不确定时间序列的分类方法UDTWL、概率性边界范围查询方法PBRQ、以及本文提出的基于Hadoop的不确定异常时间序列检测算法HUDTW。然后对比默认Hadoop集群及本文提出的优化集群在不同数据量下的时间复杂度，验证优化集群的时间高效性。实验采用的数据为无线传感器采集数据，且由于传感器采集的数据具有显著大数据特征，因而十分适合Hadoop平台下开发应用，所以实验也进一步验证了本算法在WSN环境中的高效应用。

3.1 算法的有效性分析

算法的有效性从算法的时间复杂度及算法的准确性两反面进行对比，为准确验证算法的有效性，本次实验采集五组不同大小数据集分别采用运行在Hadoop集群上的HUDTW算法、串行UDTWL算法、串行PBRQ算法测试算法的时间复杂度和精确度。

3.1.1 精确度对比

精确度对比是比较不同算法检测不确定异常时间序列的准确程度，即对比检测到的正确的不确定异常时间序列与实际不确定异常时间序列的比值。实验采集五组大小不同的数据集进行多次检测取平均值，对三种不同算法的精确度进行了科学比对，图2为多次检测所得结果。由图可知，PBRQ算法未对数据进行任何降维处理，取完整的数据信息进行检测，因而精确性极高，本文提出的HUDTW算法检测结果与之类似，同样展现了较高的准确度，UDTWL算法由于采用减枝方法一定程度上降低了算法的精确度。

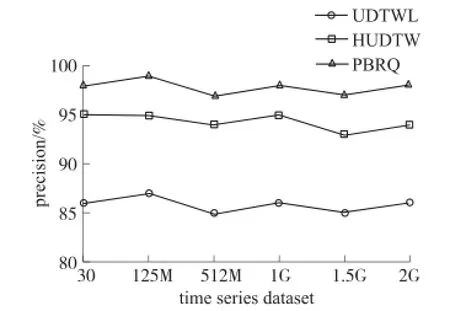
图2 不同算法精确度对比

3.1.2 时间复杂度对比

时间复杂度对比主要是不同算法执行所消耗的时间的对比。从理论上分析，PBRQ算法为最原始的判定方法，由于两条不确定时间序列的距离是由大量可能的距离组成，而PBRQ算法未对时间序列进行任何降维处理，因此，时间复杂度相对很高。UDTWL算法为一种面向不确定时间序列的分类方法，对不确定时间序列采用DTW距离进行度量，由于该算法采用了下届函数等对算法进行很好的减枝，因而复杂度低于传统的PBRQ算法。而本文提出的HUDTW算法则采用Hadoop并行框架，与上述串行算法相比复杂度自然大幅下降。实验结果由图3可知，数据量很小时，UDTWL算法时间消耗低却牺牲了精确度，PBRQ算法精确度虽高，却是以很高的时间复杂度为代价，HUDTW算法则在确保准确性的同时维持了低时间复杂度。随着数据量逐渐增大，串行算法时间消耗急剧增长甚至导致溢出，而本文提出的HUDTW算法优势逐渐明显，不仅时间复杂度低，而且维持了较高的精确度。

图3 不同算法时间复杂度对比

3.2 对比分析

由于默认Hadoop集群假想环境仍为同构的集群系统，当各节点执行能力存在差异时，易形成过多的备份任务被推测执行，造成资源浪费，引起不必要的时间消耗。而本文提出的优化集群能使各节点自适应地对运行的任务量进行调整，明显缩短集群任务的完成时间。实验采用默认Hadoop集群及优化集群（Hadoop_OP）分别执行不确定异常时间序列检测算法，数据量分别为1.0 Gbyte、1.5 Gbyte、2.0 Gbyte、2.5 Gbyte、3.0 Gbyte，算法在相同数据下多次执行取平均值，对比结果如图4所示。图4中，棕色线条代表默认Hadoop集群的运行时间，而黄色线条则代表优化集群的运行时间，不同数据下，优化集群的运行时间明显低于默认Hadoop集群，优化效果显著。

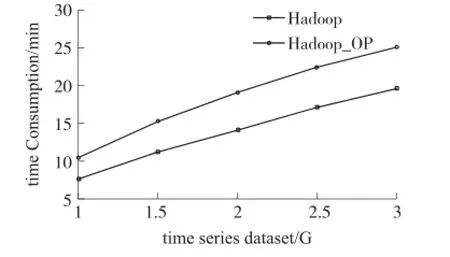
图4 不同集群时间复杂度对比

4 总结与展望

本文提出了一种基于Hadoop的不确定异常时间序列检测算法，采用Hadoop框架对海量时间序列进行并行化处理，提高检测速度，同时引入不确定时间序列压缩表示法，并提出基于期望距离的不确定时间序列的距离度量UDTW，进一步提升检测速度。实验证明此算法既减少了时间上的计算开销，又保证了准确率。本文接下来的工作是对算法的改进，进一步提高算法的精确度，同时进一步思考Hadoop集群的优化过程。

［1］ Aggarwal C C，Yu P S.A Survey of Uncertain Data Algorithms and Applications［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21（5）：609-623.

［2］ Zuo Y，Liu G，Yue X，et al.Similarity Matching over Uncertain Time Series［C］//2011 Seventh International Conference on Computational Intelligence and Security（CIS），IEEE，2011：1357-1361.

［3］ Wang Y，Wang P，Pei J，et al.A Data-Adaptive and Dynamic Segmentation Index for whole Matching on Time Series［J］.Proceedings of the VLDB Endowment，2013，6（10）：793-804.

［4］ 李斌，刘瑞琴，刘学军.基于冗余点压缩的趋势异常序列检测［J］.传感技术学报，2014，27（3）：401-408.

［5］ Aßfalg J，Kriegel H P，Kröger P，et al.Probabilistic Similarity Search for Uncertain Time Series［C］//Scientific and Statistical Database Management.Springer Berlin Heidelberg，2009：435-443.

［6］ Zhao Y，Aggarwal C，Yu P.On Wavelet Decomposition of Uncertain Time Series Data Sets［C］//Proceedings of the 19th ACM International Conference on Information and Knowledge Management.ACM，2010：129-138.

［7］ 吴红华，刘国华，王伟.不确定时间序列的相似性匹配问题［J］.计算机研究与发展，2014，51（8）：1802-1810.

［8］ 王佳林，王斌，杨晓春.面向不确定时间序列的分类方法［J］.计算机研究与发展，2011，48（suppl）：31-39.

［9］ Lu W，Shen Y，Chen S，et al.Efficient Processing of k Nearest Neighbor Joins Using Mapreduce［J］.Proceedings of the VLDB Endowment，2012，5（10）：1016-1027.

［10］Afrati F N，Fotakis D，Ullman J D.Enumerating Subgraph Instances Using Map-Reduce［C］//Data Engineering（ICDE），2013 IEEE 29th International Conference on.IEEE，2013：62-73.

［11］Fischer M J，Su X，Yin Y.Assigning Tasks for Efficiency in Hadoop［C］//Proceedings of the 22nd ACM Symposium on Parallelism in Algorithms and Architectures.ACM，2010：30-39.

［12］Chen Y，Alspaugh S，Borthakur D，et al.Energy Efficiency for Large-Scale Mapreduce Workloads with Significant Interactive Analysis［C］//Proceedings of the 7th ACM European Conference on Computer Systems.ACM，2012：43-56.

［13］郑晓薇，项明，张大为，等.基于节点能力的Hadoop集群任务自适应调度方法［J］.计算机研究与发展，2012，51（3）：618-626.

李 斌（1979-），男，江苏南京人，硕士，讲师，主要研究方向包括数据库，传感器网络等，libean@139.com；

刘学军（1971-），男，江苏南京人，副教授，博士，主要研究方向包括数据库，数据挖掘，传感器网络等。

张建平（1989-），女，江苏南通人，硕士生，主要研究方向为数据挖掘，异常检测，传感器网络；

Uncertain Abnormal Time Series Detection Based on Hadoop*

LI Bin*，ZHANG Jianping，LIU Xuejun
（College of Computer Science of Technology，Nanjing Tech University，Nanjing 211800，China）

In wireless sensor network，data collection of sensors and wireless network transmission all can produce uncertain time series.The arrival of big data age makes the detecting of uncertain abnormal time series face the problem of poor efficiency of time.So this paper proposes an algorithm about uncertain abnormal time series detection based on Hadoop.In this paper，uncertain time series are firstly compressed so that the uncertain data can be reduced greatly.Then the DTW algorithm of uncertain time series based on expected distance is called during MapReduce operation of Hadoop to realize the parallelization calculation of this algorithm.This measure reduces the time complexity greatly.Meanwhile，to solve the uneven load distribution exists in current Hadoop inherent task-level scheduling methods；the paper also proposes a method of Hadoop optimization.It not only reduces the total task completion time，but also makes the node resource utilization more reasonable.The results demonstrate that this algorithm not only decreases the time consumption，but also keeps a high precision.

wireless sensor network；uncertain abnormal time series；Hadoop optimization；compress；dynamic time warping；expected distance EEACC：7230

TP393

A

1004-1699（2015）07-1066-07

10.3969/j.issn.1004-1699.2015.07.021

项目来源：国家公益性科研专项项目（201310162，201210022）；连云港科技支撑计划项目（SH1110）

2014-12-16 修改日期：2015-04-26