遗传算法及其在非线性方程组求解中的应用研究
2015-11-17王爱华
王爱华
(南充职业技术学院,四川 南充 637131)
1 引 言
电子信息技术和网络技术飞速发展,其相关学科交叉所形成的数学模型中非线性方程组问题日益增多,其重心可归结为各种非线性方程组的求解问题.目前,关于求解非线性方程组的相关理论和方法已较成熟,但对于求解方法的有效性研究却不够深入.主要原因在于计算上所具有的复杂性容易导致求解结果陷入局部最优.本文讨论了如何改进遗传算法以及如何利用改进后的遗传算法求解非线性方程组.
2 遗传算法及其改进
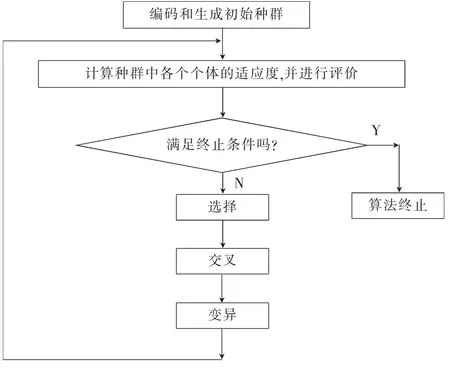
图1 基本遗传算法流程图Fig.1 Flow chart of basic genetic algorithm
2.1 遗传算法的算法流程
遗传算法是通过模拟个体组成群体的整体状况,进行选择、交叉和变异等操作,以选取搜索空间中的最优解. 其算法过程及流程图(图1)分别如下:
a)设置种群的最大进化代数T 和遗传操作算子,然后随机生成初始种群p(0);
b)对种群p(t)中每个个体进行适应度评价,并计算种群的平均适应度;
c)根据优胜劣汰,选择保留优秀个体,淘汰种群中适应度较低的个体;
d)为生成新的个体,依据选择概率,将种群之间进行交叉运算;
e)对新个体进行交叉、变异操作,计算下一代种群p(t+1);
f)对t、T 进行比较,若t >T 或等于设置精度,则这一代为最优个体,计算终止;若t≤T,则t→t+1,从第b)步继续计算.
2.2 遗传算法的收敛性
评价迭代算法性能的重要指标是收敛性和收敛速度,目前基本上都是用标准遗传算法(又称S 遗传算法)模型[1]来分析遗传算法收敛性的各种结论.
设f(Sk*)=max{f(s(1,k),s(2,k),…,s(n,k))}是第k 次进化迭代时群体{s(j,k)}中的最大适应度值为此时的群体最优串(若,则令,否则(s(1),s(2),…,S(n))}是遗传算法所求问题的全局最大适应度值,全局最优串(其中为有效基因,若在某处基因位上,群体中所有串中不存在该基因位的有效基因,则称群体有效基因缺失[1]).则当且仅当=1 成立时,称遗传算法是概率性全局收敛的.其中为的概率.
现已证明,如果在进化迭代过程中,遗传算法在保留最优串的情况下随机地以杂交和变异搜索算子,全局优化问题可通过遗传算法持续对空间进行搜索来完成,全局最优解将通过1 为概率找到,该结论称为遗传算法的极限分析定理[2].
2.3 遗传算法的不足
遗传算法虽然具有较好的全局搜索能力,但也存在不足:一是遗传算法的全局收敛性理论基础是二进制编码,对于其他编码方式还无有效证明;二是遗传算法对搜索空间进行持续搜索时,可能出现多峰优化问题,获得的最优解不一定是全局最优解,这时将重新选择此类其他基因,导致有效基因缺失,出现早熟收敛现象.
2.4 遗传算法的改进
2.4.1 采用浮点数编码方式 浮点数编码能改善由二进制编码造成的如准确度低、计算时间长、计算量大等一系列问题.在计算机中任意某个实数可近似表示为:一个整数或定点数(即尾数)乘以某个基数(计算机中通常以2 为基数)的整数次幂[3].在计算机内,浮点数可表示为如下格式:
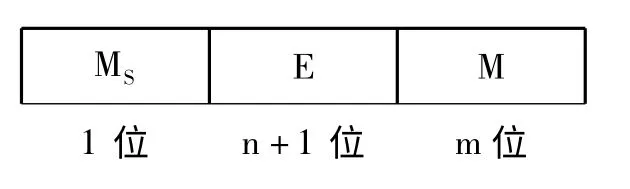
Ms 表示数的符号位,0、1 分别表示正、负号;M 表示数的尾数部分,采用定点小数形式表示,可用原码(或补码)等编码方式.
利用浮点数编码一方面可以扩大搜索范围,降低算法的复杂性,提高运算效率;另一方面可以结合其他优化方式,提高求解精度.
2.4.2 确定恰当的适应度函数 适应度函数值(遗传算法中非负)的大小决定了遗传算法的收敛效率、找到最优解的能力以及被遗传到下一代的概率.
在许多实际问题中,往往需要求最小费用,这时可将求最小目标根据适应度函数非负原则转换为求最大目标的形式,变换关系式为:

式(1)中,f(m)为适应度函数,g(m)为目标函数,m 为模型参数,Cmax为一个待定的、合适的且相对较大的实数.选择Cmax方式有:事先指定的一个较大(小)的数;进化到当代为止的最大(小)目标函数值;当代或最近几代群体中的最大(小)目标函数值[4].
此外,因遗传算法还存在另一些问题,比如对参数选择敏感、进化过程中早熟收敛而后期收敛停滞等.这时又可通过另一种变换(Goldberg 线性比例变换)来解决,变换公式为:

f(x)、g(x)分别为变换前后的适应度函数值.
根据概率式转移规则,由种群中各个体的适应度大小确定下一步搜索方向.事实上,使用(1)和(2)式计算所得出的个体适应度值,不会让所有问题结果收敛速度一致,需要降低较高的个体适应度值克服早熟,增加较低的个体适应度值避免后期停滞[5].
2.4.3 搜索遗传算子 遗传算子主要有三种类型:复制算子(reproduction)、杂交算子(crossover)和变异算子(mutation)[6],因为遗传算法是通过一系列的遗传算子来进行的,所以搜索遗传算子有较重要的作用,步骤如下:
第一步:选择算子
采用的选择概率计算方式为:

其中n 为种群大小,i 为个体排序序号,η+∈[1,2],η-=2 -η+.
遗传算法在选择时容易出现个别个体在种群中迅速繁殖,个体适应度彼此非常接近,搜索不能有效进行.这时可采用变换适应度函数尺度大小的方法来解决,即令:
第二步:交叉算子
遗传算法中的交叉操作体现了信息交换的思想,即子代包含了父代的信息特征.交叉算子是一种进化计算,通过它可生成基因更加优良的个体.交叉算子的设计和实现要求在产生优良的新个体情况下又不能破坏表现优良的编码串模式.在交叉时要注意,必须严格控制好交叉概率,交叉概率过大可能破坏遗传模式,交叉概率过小则不易产生新个体.
第三步:变异算子
变异算子的作用是通过调整个体编码中的部分基因值大小来改善遗传算法的局部搜索能力,让从局部出发搜索所得的个体最大程度地逼近最优解.同时,算子因基因值的新旧替换而得到变异,改变了个体编码串的结构,保持了种群的多样性,防止早熟[5].
3 基于改进后的遗传算法对于非线性方程组的求解
3.1 非线性方程组的定义
非线性方程组是关于n 个变量的n 个方程,一般形式为:

3.2 非线性方程组的两种求解方法
3.2.1 非数值算法 以往对非线性方程组的求解,所选择的算法在计算时比较复杂.如:Newton 法、直线迭代法等.运用等价思想,将非线性方程组的求解转为函数优化问题,如下式:

其中Φ 为方程组解的区间,并且当F(X)取最大值1 时,对应的为非线性方程组的解,其具体解法笔者在此不再作赘述.
3.2.2 爬山算法[7]爬山搜索是向值增加的方向持续移动的简单循环过程——登高(从单独的当前一个状态出发,移动到与之相邻的状态(见图2)).它将会在达到一个“顶峰”(相邻状态中没有比它更高的值)时终止.爬山搜索是局部最优搜索,适合于最优化问题.
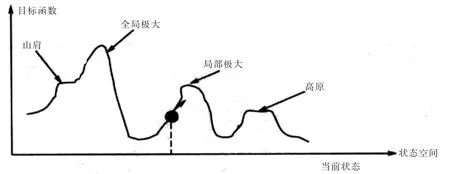
图2 最优化问题Fig.2 Optimization problem
爬山搜索法趋于在得出解答前减少需访问的节点数,因此适用于很多场合.但是,它可能存在三种弊病.一是虚假山峰的问题,此时搜索求解将涉及到大量的回溯;二是“平稳地带”问题,此时所有可能的下一步搜索的好坏程度都一样,那么爬山法就不如深度优先搜索法好;三是“山脊”问题,运算时在回溯中将数次越过山脊,爬山算法无效.
3.3 用改进后的遗传算法求解非线性方程组的可行性分析
可见,遗传算法局部搜索能力较差且存在“早熟”现象,爬山算法又难以对全局进行求解.如果综合爬山算法和遗传算法的优缺点,既可避免爬山算法的缺点,又可提高遗传算法的局部搜索能力,将使求解非线性方程组问题得到有效解决.
3.4 用改进后的遗传算法求解非线性方程组的具体步骤
根据以上分析,用改进后的遗传算法求解非线性方程组的执行步骤可总结如下:
(1)将非线性方程组问题转化为函数优化问题求解;
(2)确定策略变量、定求解空间、交叉、变异概率等,并设置变量上下限;
(3)确定编码方式;
(4)计算第一代种群适应度,确定个体的优劣状况;
(5)对种群进行寻优,结合跨世代精英选择策略和锦标赛选择法进行选择操作;
(6)根据自适应交叉、自适应变异概率及自适应爬山算子进行交叉操作、非均匀变异操作作局部搜索;
(7)寻找最优个体,并进行判断,确定非线性方程组的最优解.
4 结束语
综上,通过采用浮点数编码方式、确定恰当的适应度函数及搜索遗传算子等三个方面可对遗传算法进行改进.用改进后的遗传算法求解非线性方程组,将改观遗传算法的全局收敛和爬山算法的局部收敛现象,有效降低求解非线性方程组的复杂度,提高解的准确度.
[1] 李 楠.考虑完整交易费用组合投资模型的混合遗传算法求解[D]. 天津大学硕士论文,2005.
[2] 王学凤.金盆水库优化调度研究[D].西安理工大学硕士论文,2003.
[3] 刘正红.浮点数的教学难点及对策[J].网友世界,2012(16):231 -233.
[4] 蔡松柏,沈蒲生.关于非线性方程组求解技术[J].湖南大学学报(自然科学版),2011,27(3):189 -192
[5] 任文杰.人工神经网络在地基土液化判别及等级评价中的应用[D].河北工业大学硕士论文,2002.
[6] 黄海滨.遗传算法中遗传算子的分析[J].玉林师范学院学报,2001(09):25 -27.
[7] 张庆雅.杨火箭发动机法兰连接系统模糊可靠性分析[D].西北工业大学博士论文,2003.
