随机利率和分数跳-扩散过程下的幂期权定价
2015-11-17邓小华冯世强
邓小华,冯世强
(1.四川广播电视大学,四川 成都 610073 ;2.西华师范大学数学与信息学院,四川 南充 637009)
1 引 言
随着数理金融的蓬勃发展,期权定价问题逐渐成为计量经济学和金融数学研究的热点.已经从经典的B-S 模型,发展到欧式期权、亚式期权、实物期权的研究.一方面,偏差因素的随机性越来越高,无限地贴近交易市场的实际情形,如标的资产的价格、预期收益率、波动率和利率从常数转变为时间t 的随机函数.另一方面,诞生了越来越多的新型期权.幂期权就是其中一种典型的新型期权.幂期权根据到期日的执行条件不同分为两类,每一类都有看涨和看跌两种情形.它与标准期权的主要区别在于:持有人在期权到期日不仅可以得到一个标准的价值损益,还能将这个价值损益提高到它的n 次幂. 如:在到期日,看涨幂期权的价值为-K(其中,K 是执行价格,ST是到期日标的资产的价格,n∈N*).由此,两类幂期权在到期日的价格可以表示为如下形式[1]:
1)第一类幂期权:

2)第二类幂期权:

幂期权的研究受到国内外学者们的广泛关注.Blenman,Clark[2]考虑了B1ack-schok 模型下幂式交换期权的价值;赵巍[3]提出用测度变换方法解决随机幂式期权的定价模型;苏小囡等[4]假设标的资产价格服从跳-扩散过程,市场利率满足Vasicek 模型,当随机利率与资产价格相关时,通过测度变换的方法,选取不同的概率测度,给出幂式期权的价格公式并得到几种特殊情况时的结论;李超[5]假定股票价格服从分数O-U过程,利率服从分数Vasicek 利率模型,利用风险中性定价公式及随机分析理论等,给出两类欧式幂型看涨、看跌期权的定价公式;笔者[6]也曾在随机利率环境下,研究了标的资产价格服从分数O-U 过程的幂期权定价问题,得到相应的定价公式.上述模型中,标的资产的价格大都基于Brown 运动.但在现实市场中,突发事件是不可避免的,如:自然灾害,政府政策变化等.它们会对金融市场产生巨大影响,导致股价、汇率等出现大幅度的跳跃.Merton 于1976年首次引入跳-扩散模型[7],在几何Brown 运动上加入刻画市场突发事件引起标的资产价格波动的复合Poisson 过程.实证研究表明,跳-扩散模型更切合实际.同时,标的资产的对数收益率服从一种“尖峰厚尾”的分布,存在长期相关的分形特征.
本文假设期望收益率和波动率均为关于时间t 的非随机函数,在扩展的Vasicek 利率模型和分数跳-扩散模型下,导出了两类幂期权的看涨(看跌)定价公式.
2 模型介绍
2.1 分数Brown 运动下的积分定义
分数Brown 运动具有长期依耐性、自相似性等特征,是一个连续的Gauss 过程{BH(t),t∈R},BH(0)=0,E(BH(t))=0,CH(t,s)=(|t|2H+ |s|2H- |t-s|2H)/2 .其中,0 <H <1,H 称为Hurst 指数.当H =0.5 时,BH(t)即为几何Brown 运动B(t);当H≠0.5,{BH(t),t∈R}既不是马氏过程,也不是半鞅,因此不能用通常的随机积分理论来分析.文献[8]用Wick 积和分数噪声理论定义了H >0.5 时的一种随机积分:

其中,◇为Wick 积.
2.2 Vasicek 利率模型
在分数风险中性测度Q 下,假设利率r(t)满足如下的随机微分方程:

其中:a(t)描述利率的长期水平,b(t)是调整短期和长期关系的均值回复率;BQ(t)为风险测度Q 下的几何Brown 运动,记其与分数Brown 运动的相关系数为ρ,σr(t)是波动率.这就是扩展的Vasicek 模型[6].
2.3 分数跳-扩散模型
若把跳-扩散模型中的几何Brown 运动B(t)扩展为分数Brown 运动BH(t),就得到分数跳-扩散模型.即标的资产价格过程{S(t):t≥0}满足随机微分方程:

其中,{BH(T),0≤t≤T}为概率空间(Ω,F,P)上的分数Brown 运动,r(t)是t 时刻的短期利率,它等于期望收益率,σ(t)是t 时刻的波动率;Qt为标的资产价格在时间段[0,t]内发生随机跳跃的次数,它是服从参数为λ 的Poisson 过程,J(t)表示跳跃的相对高度,θ=E[J(t)]且ln(1 +J(t))~N(ln(1 +θ)-δ2/2,δ2),
由式(2)两边同除以S(t),有
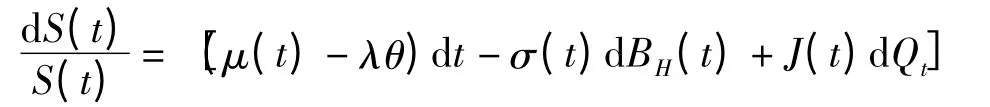
由分数Brown 运动下的积分定义(1),得到(详见文献[8]):

2.4 引理[6]:
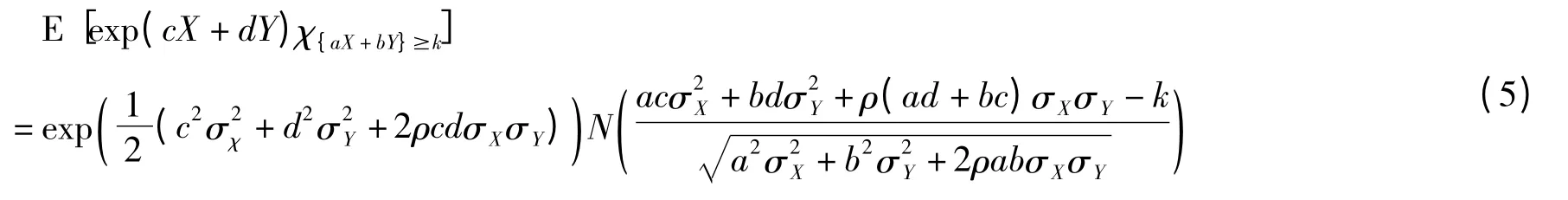
3 期权定价公式及其证明
3.1 第一类幂期权的定价
定理1:假设利率满足扩展的Vasicek 模型(2),标的资产价格满足分数跳-扩散模型(3),且在[0,t]内发生n 次跳跃,若执行价格为K,到期日为T,则第一类看涨幂期权在到期前任意时刻t 的价格为:

N(·)表示标准正态分布的累积概率.
证明:根据无套利定价理论,第一类看涨幂期权在时刻t 的价格

记EQ[·]为分数风险中性测度Q 下的拟条件数学期望算子,,则有

式(7)中第一项的计算:由式(4)和引理,有

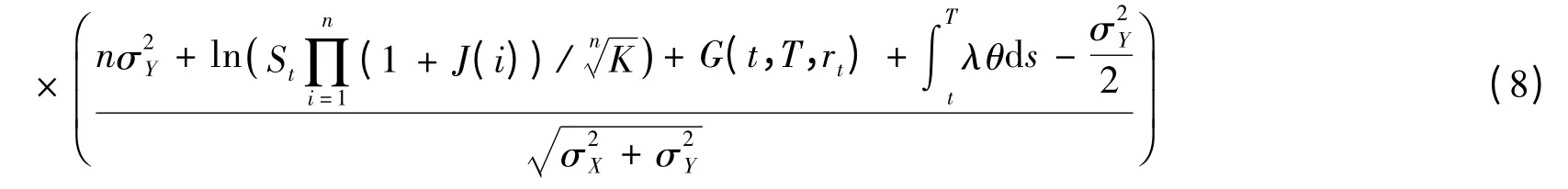
同理,可以计算式(7)中的第二项,如下:

将以上两式的结果带入式(7),从而得到式(6)的结果.证明完成.
由看涨-看跌平价关系,很容易得到第一类看跌幂期权在到期前任意时刻t 的定价公式.
定理2:假设利率满足扩展的Vasicek 模型(2),标的资产价格满足分数跳-扩散模型(3),且在[0,t]内发生n 次跳跃,若执行价格为K,到期日为T,则第一类看跌幂期权在到期前任意时刻t 的价格为:

其中:N(·)表示标准正态分布的累积概率,
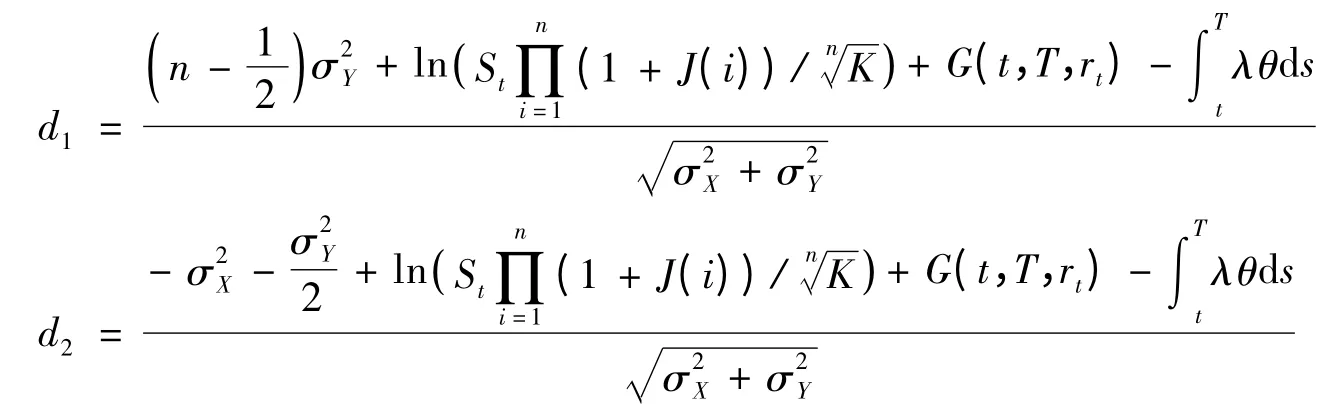
注:1)当J(t)=0,H=0.5 时,定理1 和定理2 就是随机利率下第一类看涨(跌)幂期权的定价公式.2)当σr(t)=0,H=0.5 时,定理1 和定理2 就是跳扩散模型下第一类看涨(跌)幂期权的定价公式.3)当J(t)=0 时,定理1 和定理2 的定价公式与文献[5]中随机利率和分数布朗运动下幂期权的定价公式对应等价.
3.2 第二类幂期权的定价
定理3:假设利率满足扩展的Vasicek 模型(2),标的资产价格满足分数跳-扩散模型(3),且在[0,t]内发生n 次跳跃,若执行价格为K,到期日为T,则第二类看涨幂期权在到期前任意时刻t 的价格为:


证明:根据无套利定价理论,有

由引理,将式(4)代入,得到

将式(13)和式(14)代入式(12),得到定理3 的结论.证明完成.
由看涨-看跌平价关系,很容易得到第二类看跌幂期权在到期前任意时刻t 的定价公式.
定理4:假设利率满足扩展的Vasicek 模型(2),标的资产价格满足分数跳-扩散模型(3),且在[0,t]内发生n 次跳跃,若执行价格为K,到期日为T,则第二类看跌幂期权在到期前任意时刻t 的价格为:


注:1)当J(t)=0,H=0.5 时,定理3 和定理4 就是随机利率下第二类看涨(跌)幂期权的定价公式.2)当σr(t)=0,H=0.5 时,定理3 和定理4 就是跳扩散模型下第二类看涨(跌)幂期权的定价公式.3)当J(t)=0 时,定理3 和定理4 的定价公式与文献[5]中随机利率和分数布朗运动下幂期权的定价公式是对应等价的.
4 结 论
本文考虑利率的随机性和标的资产价格的跳跃性,在随机利率和分数跳-扩散过程下研究了两类幂期权的无套利定价.运用无套利定价原理和随机微分理论,导出并证明了两类看涨(跌)幂期权的定价公式,使文献[5]的结果得到了相应的扩展.
[1] 赵佃立.分数布朗运动环境下欧式幂期权的定价[J].经济数学,2007,24(1):22 -26.
[2] BLENMAN L P,CLARK S P. Power exchange options[J].Finance Research Letters,2005 (2):97 -106.
[3] 赵 巍,何建敏.基于测度变换方法的随机型创新幂式期权定价[J].中国管理科学,2009 ,17 (2):21 - 23.
[4] 苏小囡,王文胜.幂式期权在跳扩散模型下的定价[J].华东师范大学学报,2011,5(3):12 -20.
[5] 李 超.分数维Vasicek 模型下欧式幂型期权的定价公式[J].中国科技信息,2014,2:167 -170.
[6] 邓小华,何传江,方 知.随机利率下服从分数O-U 过程的幂期权定价[J].经济数学,2009,26(1):64 -71.
[7] MERTON R C. Option pricing when underlying stock return are discontinuous[J].Journal of Economics,1976(3):125 -144.
[8] HU Y,ФKSENDAL B. Fractional white noise calculus and applications to finance[J]. Infinite Dimensional Analysis,Quantum Probability and Related Topics,2003,6:1 -32.
