单位圆盘的拟对称映射不具有Landau定理

冯小高

(西华师范大学数学与信息学院，四川 南充 637009)

1 引 言

20 世纪早期，Landau 证明了:存在一正数，若f(z)为单位圆盘D={z:|z| ＜1}上任意的解析函数，且满足正规化条件:f'(0)=1，则像集f(D)包含一个至少以此正数为半径的圆盘． 最优的这个正常数为Landau常数．在1925年，Andre Bloch 进一步证明了:存在一正数，若f(z)为单位圆盘D ={z:|z| ＜1}上任意的正规化解析函数，则f(z)将单位圆盘D={z:|z| ＜1}内一开子集一一的映到至少以此正数为半径的圆盘．最优的这个正常数为著名的Bloch 常数．

近来，Gauthier 和Pouryayevali 在［1］中证明了在平面内对多项式拟共形映射不具有Landau 定理．借助Gauthier 和Pouryayevali 的方法，构造了一个拟对称映射的例子，通过Vaisala 的一个结论，证明了构造的映射为拟对称映射，根据此映射中参数ε ＞0 的任意性，说明了在平面上拟对称映射不具有Landau 定理．下面先回忆一下一些基本概念．

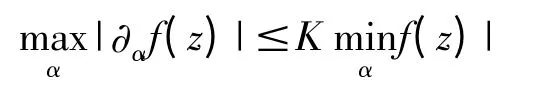
则称f(z)为K-拟共形映射．

定义2 假设η:［0，∞)→［0，∞)为单调增，A⊂C，C 代表复平面，若对任意不同的三点z1，z2，z3∈A，有

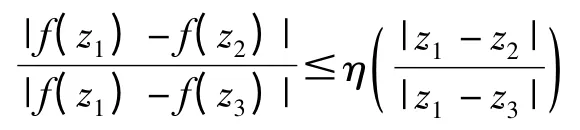
则称f(z)为η 拟对称映射．

在［2］中讨论了拟共形映射与拟对称映射的关系:在局部情况下，拟对称映射和拟共形映射是等价的．从此角度，根据Gauthier 和Pouryayevali［1］的结果和拟对称映射与拟共形映射的局部等价性，自然有拟对称映射不具有Landau 定理．但我们通过Vaisala［3］的一个结论，说明构造的映射为拟对称映射，从而证明了在平面上拟对称映射不具有Landau 定理．

2 主要结论和证明

先介绍一个引理

引理2．1［3］假设Ω 和Ω'为复平面C 的子区域，f:ˉΩ→ˉΩ'为同胚，且满足:f|Ω为K-拟共形映射，f|∂Ω为η-拟对称映射．则f 为η1-拟对称映射，η1只与K 和η 相关．

定理 对任意的K ＞1，和任意的ε ＞0，存在拟对称映射f(z)，使其满足:fz(0)=0，且f(D)包含在以ε ＞0为半径的圆盘内．

证明:对K ＞1 和t ＞1，令

h(s)=(1 -K)lnt+Ks，

构造映射

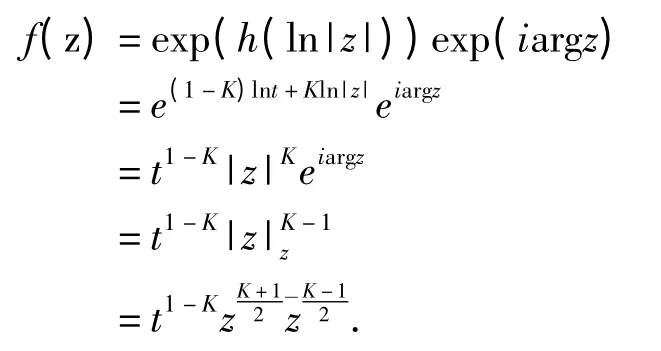
首先证明上面定义的f(z)为单位圆盘上的K-拟共形映射．由f(z)的定义得其两个偏导数为

根据(1)和(2)知Jacobi 行列式

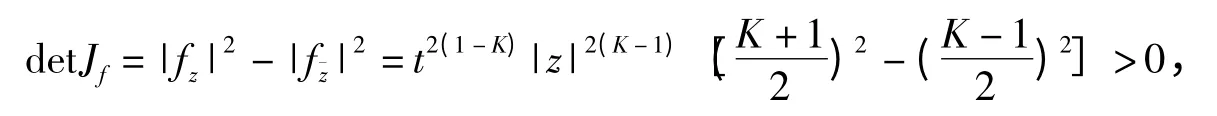
且最大伸缩商

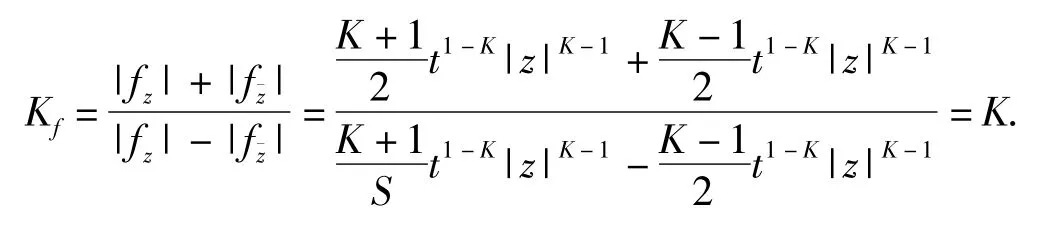
所以f(z)为单位圆盘上的K-拟共形映射．

下面说明上面定义的为拟对称映射．

对任意不同的三点z1，z2，z3∈∂D={z:|z| =1}，因为对函数η(t)=ct(c≥1)，有

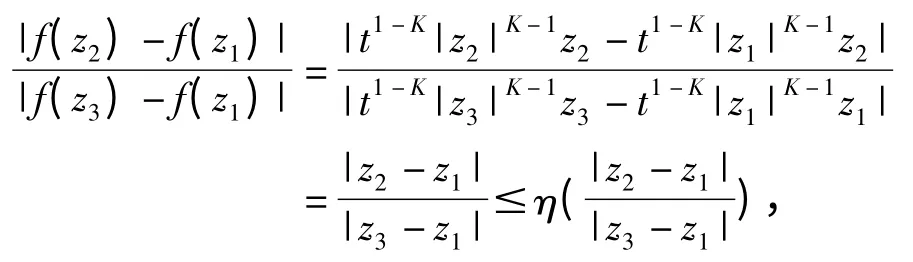
则f(z)在∂D={z:|z| =1}上为η-拟对称映射，又由于f(z)在单位圆盘内为K-拟共形映射，根据引理2．1知f(z)为η' -拟对称映射，且f(D)包含在以ε=t1-K＞0 为半径的圆盘内．

由定理中ε=t1-K＞0(注意t ＞1)的任意性，易知下面推论．

推论1 在平面上单位圆盘的拟对称映射不具有Landau 定理．

推论2 在平面上单位圆盘的拟对称映射不具有Bloch 定理．

［1］ GAUTHIER P M，POURYAYEVALI M R，Failure of Landau'theorem for quasiconformal mapping of the disk［J］．Contermporary Mathematics，2004，355:265 -268．

［2］ ASTALA K，LWANIEC T，and MARTIN G，Elliptic partial differential equations and Quasiconformal mappings in the plane［M］． Princeton University press．2009．

［3］ VAISALA J，Quasisymmetry and unions［J］． Manuscripta Mathematica，1990，68:101 -11．