基于解析法的HSK主轴-刀柄结合部参数辨识

陈建，田良，商宏谟，郑登升，王贵成，3

（1.江苏大学机械工程学院，江苏镇江212013；2.成都工具研究所有限公司，四川成都610051；3.南通理工学院，江苏南通226002）

基于解析法的HSK主轴-刀柄结合部参数辨识

陈建1，田良2，商宏谟2，郑登升1，王贵成1，3

（1.江苏大学机械工程学院，江苏镇江212013；2.成都工具研究所有限公司，四川成都610051；3.南通理工学院，江苏南通226002）

辨识HSK主轴-刀柄结合部参数，是准确预测主轴系统动态特性及保证切削稳定性的基础条件。将HSK主轴-刀柄结合部简化为弹簧-阻尼模型。再根据HSK主轴-热装刀柄系统的频率响应矩阵，推导出HSK主轴-刀柄结合部的刚度矩阵。并基于耦合响应法计算热装刀柄两端的频响矩阵，利用有限差分法与实验测量相结合的方式，分别获得HSK主轴端点和HSK主轴-热装刀柄系统端点的频响矩阵。基于推导出的结合部刚度矩阵，分别辨识出HSK主轴-刀柄结合部的4个刚度参数kyf、kθf、kym和kθm，以及4个阻尼参数cyf、cθf、cym和cθm.使用耦合响应法计算出HSK主轴-热装刀柄端点的频响函数，并与实验测量的各阶频率相比较，理论频率与实验结果最大差值为7.9%，进而验证辨识参数的准确性和辨识方法的合理性。

机械制造工艺与设备；HSK主轴-刀柄结合部；频响矩阵；参数辨识

0 引言

HSK主轴-刀柄-刀具系统被广泛应用于高速和高精密加工，系统颤振严重影响加工质量和加工效率。准确的稳定性叶瓣图（切削速度-切削厚度关系图）是避免颤振和保证切削稳定性的必要条件。但无论采用何种方法获得叶瓣图，都需要先得到机床主轴系统刀尖点的频率响应函数［1］。其中，准确的结合部参数又是精确预测主轴系统刀尖频率响应函数的前提和保证。本文以HSK主轴-刀柄系统为研究对象，并采用解析法对HSK主轴-刀柄结合部进行参数辨识。

结合部一般都简化为弹簧-阻尼模型。Schmitz等［2］使用有限元法对热装刀柄-刀具结合部进行参数辨识，并获得了结合部内各位置的刚度和阻尼参数，但只获得两个阻尼参数，而且为阻尼与频率的乘积cω.Namazi等［3］采用有限元与实验相结合的方法来辨识结合部参数，此方法只获得了结合部内各位置的平动刚度和转动刚度，但其计算量很大，也没有考虑结合部的阻尼参数。程强等［4］基于子结构耦合法和最小二乘法对BT40主轴-刀柄结合部进行了参数辨识，此方法只获得了结合部内部各个位置的平动刚度，没有辨识结合部的转动刚度和阻尼参数。基于以上方法的优缺点，提出采用有限差分法与实验相结合的方式来辨识HSK主轴-刀柄锥面结合部的刚度和阻尼参数。

1 HSK主轴-刀柄结合部的研究思路及理论基础

1.1 HSK主轴-刀柄结合部的研究思路

HSK主轴-刀柄系统可简化为主轴和刀柄通过弹性耦合而成的系统，如图1所示。HSK主轴和刀柄都简化为多段Timoshenko梁，并通过刚度矩阵KSH将二者进行弹性耦合，可得HSK主轴-刀柄系统端点的频响函数矩阵［5-6］:

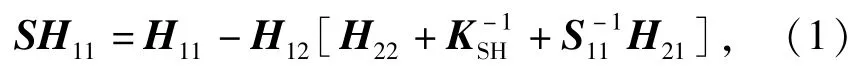
式中:下标1为单段热装刀柄的右端点，2为单段热装刀柄的左端点，如图1所示。对（1）式进行变化，由此可得到HSK主轴-刀柄结合部刚度矩阵为

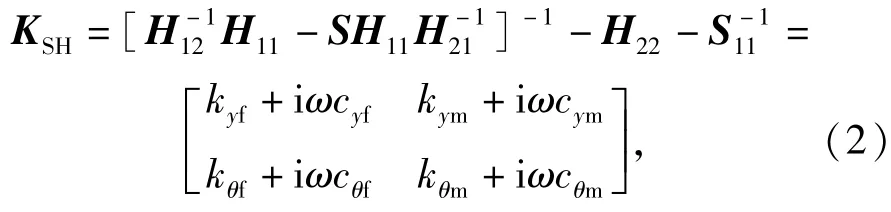
式中:kyf和kθf分别为受力载荷下的平动刚度和转动刚度；kym和kθm分别为受力矩载荷作用下的平动刚度和转动刚度；cyf和cθf分别为受力矩载荷下的平动和转动阻尼；cym和cθm分别为受力矩载荷下的平动和转动阻尼。

图1 HSK主轴-刀柄弹性耦合Fig.1 Flexible coupling of HSK spindle-toolholder

为获得HSK主轴-刀柄结合部参数，需要获得刀柄两端的响应矩阵H11、H12、H21和H22，以及HSK主轴端点的响应矩阵S11和HSK主轴-刀柄系统端点的SH11.由于HSK主轴-刀柄结合部刚度和阻尼满足Betti-Maxwell的弹性互易定理［7］，因而可假定kym=kθf和cym=cθf，故HSK主轴-刀柄结合部的刚度矩阵KSH为对称矩阵。

1.2 基于耦合响应法的频响矩阵

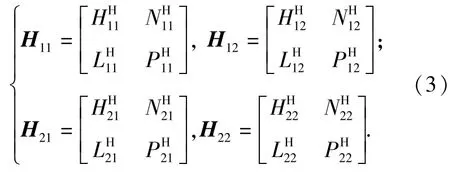
刀柄的响应矩阵可采用耦合响应法来计算，并将刀柄简化为多段的Timoshenko梁，刀柄两端的频响矩阵为

以上各个元素可以表示为

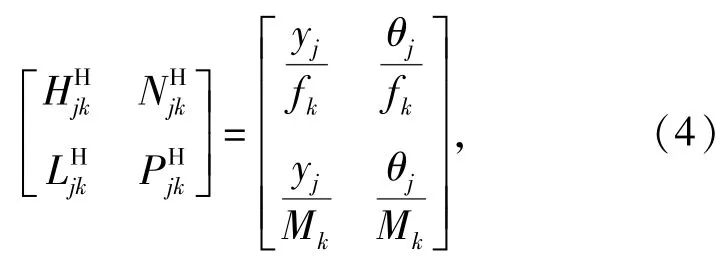
式中:y为平动位移；θ为转角；f为作用力；M为力矩；下标为刀具的作用点。矩阵Hjk各元素［8］为

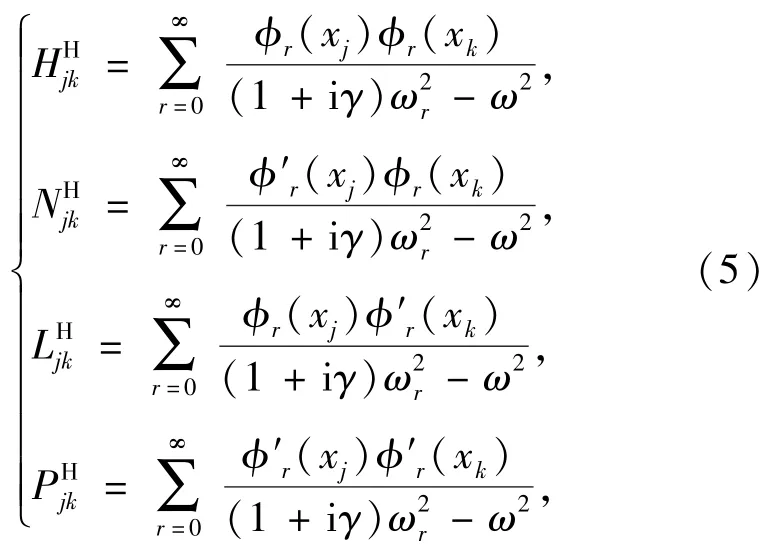
计算频响函数时，将HSK主轴和热装刀柄都简化为多段Timoshenko梁。j为单段热装刀柄或HSK主轴的端点编号，k为力或力矩作用在单段热装刀柄或HSK主轴的端点编号，其中:j=1，2；k=1，2. 1为单段梁的右端点，2为单段梁的左端点，如图1所示。

1.3 基于有限差分法的测量频响矩阵

HSK主轴端点频响矩阵S11和HSK主轴-刀柄系统端点的频响矩阵SH11为

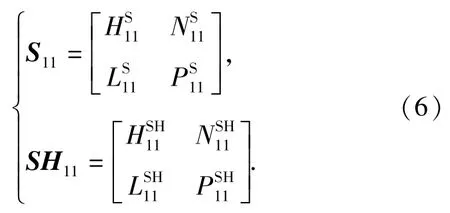
响应矩阵不仅包括受力作用下的位移和转角频响函数，还包括受力矩作用下的位移和转角频响函数。如果只采用实验方法获得相应的频响函数，需先在HSK主轴和HSK主轴-热装刀柄系统端点处分别安装位移传感器和角度传感器，并在对应位置上加载力和力矩，便可直接测量获得受力和力矩作用下的位移频响函数和转角频响函数。但实验测量所需传感器多，增加了实验成本；而且，实验测量数据多，测量效率低。为简化实验步骤和减少测量仪器，提出采用有限差分法与实验测量相结合的方式来获得测量响应矩阵，只需位移传感器，并按照有限差分原理将传感器直线布置在被测件上，如图2所示。测量响应矩阵可通过1阶有限差分或2阶有限差分获得。1阶有限差分所需测量值最少，只需测量图2中的两个点B和C，2阶有限差分需要测量3个点A、B和C.Duarate等［9］指出使用有限差分法获得的测量响应矩阵精度，严重依赖于测量点的阶数和间隔距离。图2传感器的位置为并联谐振，频率随着间隔距离的增加或者减少都会发生偏移。综合考虑，本文选用2阶有限差分法来测量HSK主轴和HSK主轴-刀柄系统的响应矩阵。

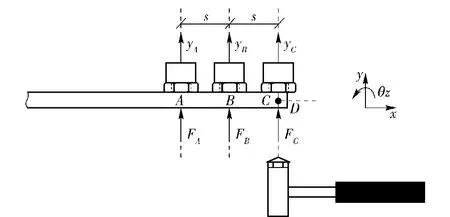
图2 有限差分法示意图Fig.2 Finite difference method

使用2阶有限差分法获得的测量频响矩阵为

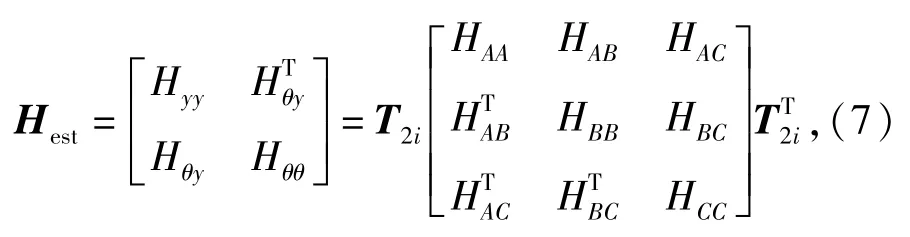
式中:HAA、HAB等为各个点受力作用下的位移频响函数，都是通过上述实验方法测量得到；T2i为2阶差分转化矩阵。当力锤作用点P=A或者P=C时，2阶差分的前插、中插和后插转化矩阵为

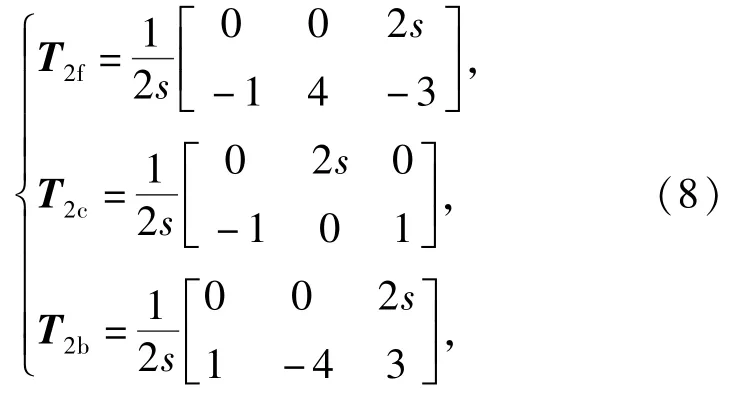
式中:s为传感器间隔距离。前插和后插转化矩阵只是最后一排符号不一致，这些矩阵具有相同的精度。将（8）式代入到（7）式中，由此可得测量频响矩阵为

本文以后插转化矩阵计算得到的测量频响矩阵作为HSK主轴端点和HSK主轴-热装刀柄系统端点的频响矩阵，只需将测量的受力作用下的位移频响函数代入到（9）式中，便可获得HSK主轴端点和HSK主轴-刀柄系统端点的频响函数。

2 HSK主轴-刀柄结合部参数辨识

2.1 基于耦合响应法计算刀柄频响矩阵

本文选择的主轴类型为HSKA63，刀柄为热装刀柄［10］，弹性模量E=500 MPa，密度ρ=7 850 kg/m3，泊松比μ=0.22，如图3所示。将热装刀柄简化为多段Timoshenko梁，并采用耦合响应法来计算热装刀柄的频响函数。其中，分段的数量与计算的频响函数精度密切相关，分段越多、计算精度越高，而计算量会大大增加。因此，综合考虑计算精度和计算量，本文以HSK热装刀柄的关键尺寸为依据，并以刀柄柄部左端为起始段，来对HSK热装刀柄进行分段处理。图4为HSK热装刀柄分段划分图，具体分段尺寸如表1所示。先分别计算每段梁的频响函数，再对每段梁进行刚性耦合，进而获得整个部件的频响函数。单段梁频响函数G11的计算如图5所示，梁的两端点分别表示为1和2.使用质量集中方程可以建立相应的响应方程，并将与线性和转动位移有关的力和力矩应用到这些点上。

图3 HSK主轴-刀柄系统Fig.3 HSK spindle-toolholder system

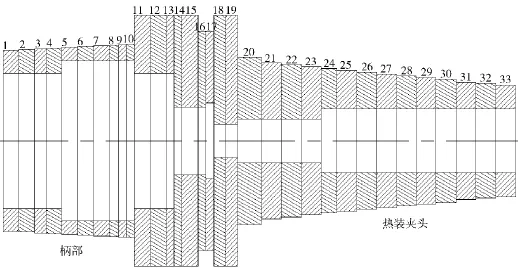
图4 HSKA63热装刀柄分段划分图Fig.4 Multi-segments of HSKA63 shrink toolholder

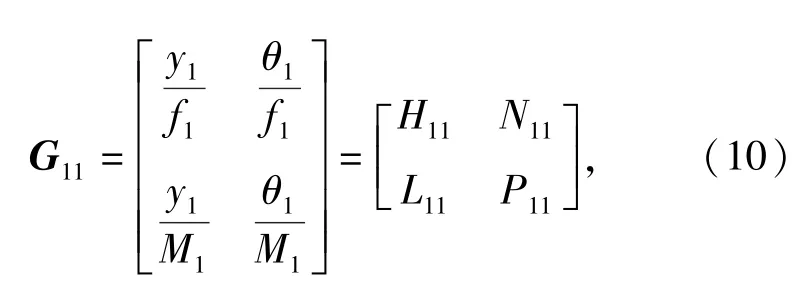
式中:点1的频率响应函数根据（5）式来计算。图6（a）所示，两段Timoshenko自由端梁可以耦合为一段自由端梁。其中，自由端响应矩阵A和B可以表示为

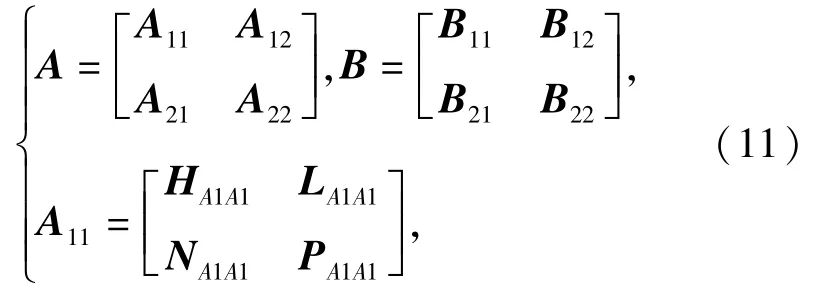
式中:AA1A1可简单表示为A11.当得到梁A和B的位移-力（力矩）矩阵后，考虑到连接点的兼容性和连续性，可以得到两段梁的耦合矩阵C为

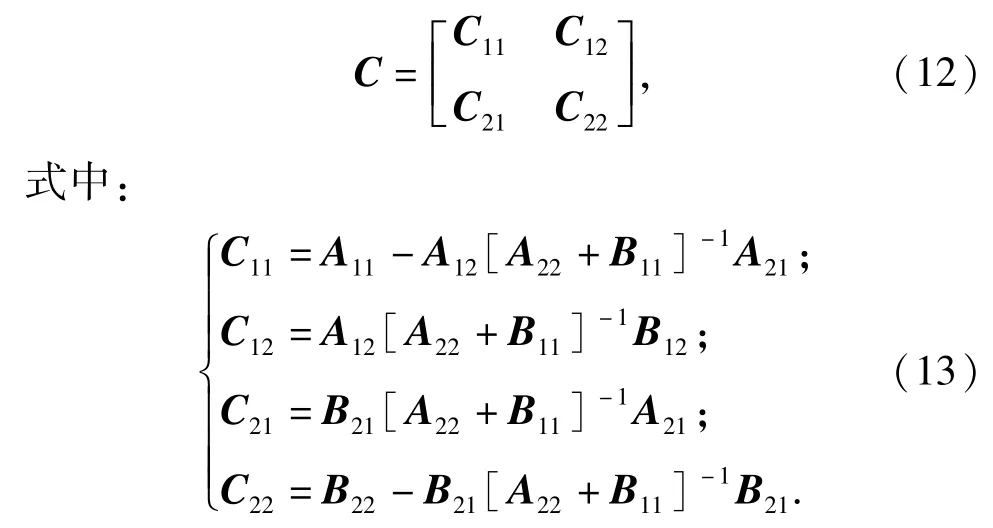
同理，可采用相同的方法对多段梁进行刚性耦合，如图6（b）所示。通过这样的方式，将不同直径和长度的梁进行刚性耦合，可计算得到HSK热装刀柄的频响函数。由于本文所要辨识的刚度矩阵KSH为对称矩阵，因而在计算热装刀柄端点响应矩阵H11、HSK主轴端点响应矩阵S11和HSK主轴-热装刀柄系统端点响应矩阵SH11过程中，都可假定力矩作用下的频响函数N与力作用下的转角频响函数相等L，即N=L.图7为频响矩阵H11的4个频响函数图。

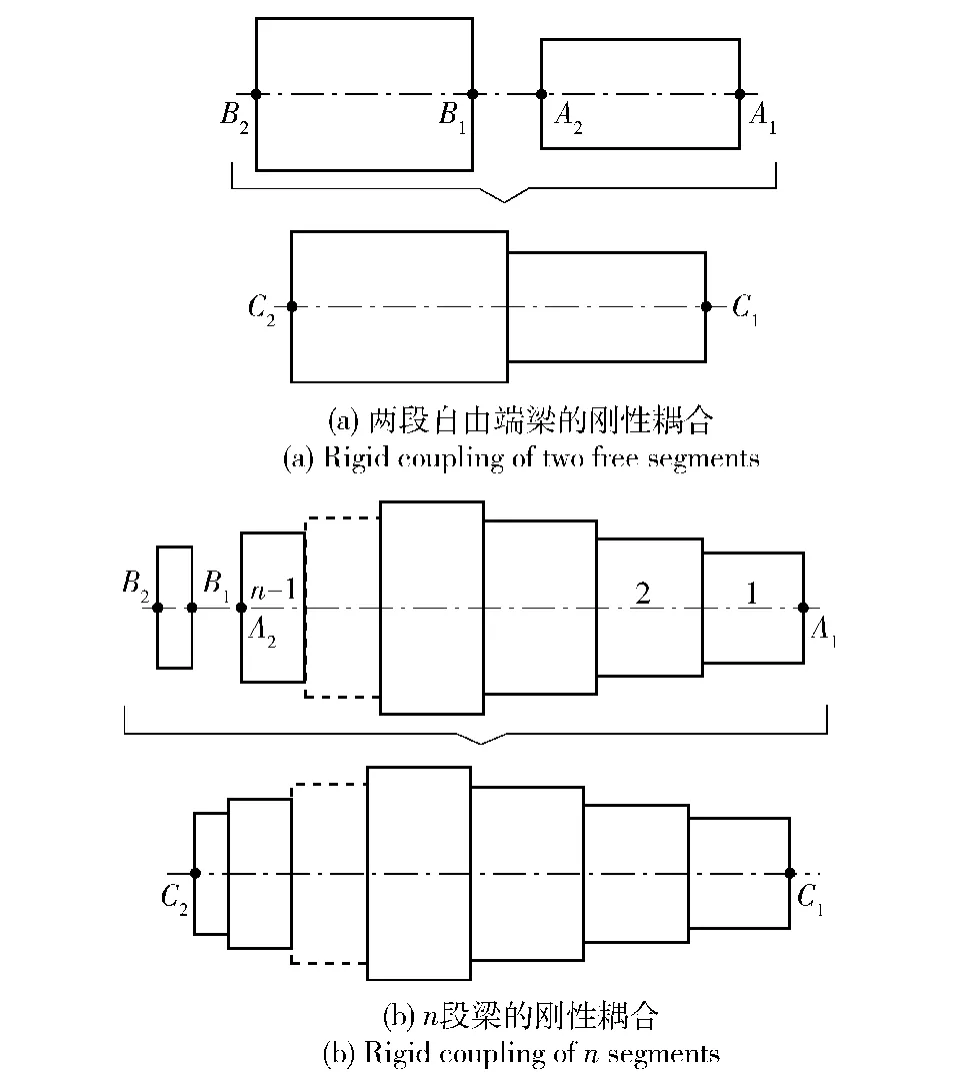
图6 多段自由端梁的刚性耦合Fig.6 Rigid coupling of beams

2.2 基于有限差分法的测量频响矩阵

本文采用2阶有限差分与实验相结合的方式来获得HSK主轴和HSK主轴-刀柄系统端点的响应矩阵。本文先建立HSK主轴和HSK主轴-热装刀柄系统的有限元模型，并进行谐响应分析；然后，选择不同的间隔距离，并进行实验测量；再将实验所得频响函数与谐响应分析结果相比较，最终确定HSK主轴-热装刀柄系统和HSK主轴的最优间隔距离为35 mm和30 mm［9］。先分别将HSK主轴和HSK主轴-刀柄系统置于自由状态；再根据2阶有限差原理将加速度传感器分别安装在HSK主轴和HSK主轴-刀柄系统端点上；最后，使用力锤敲击各传感器相对应点处，测量信号通过加拿大Cutpro测试系统进行放大、采集和快速傅里叶变换，图8为频响函数测量系统图。

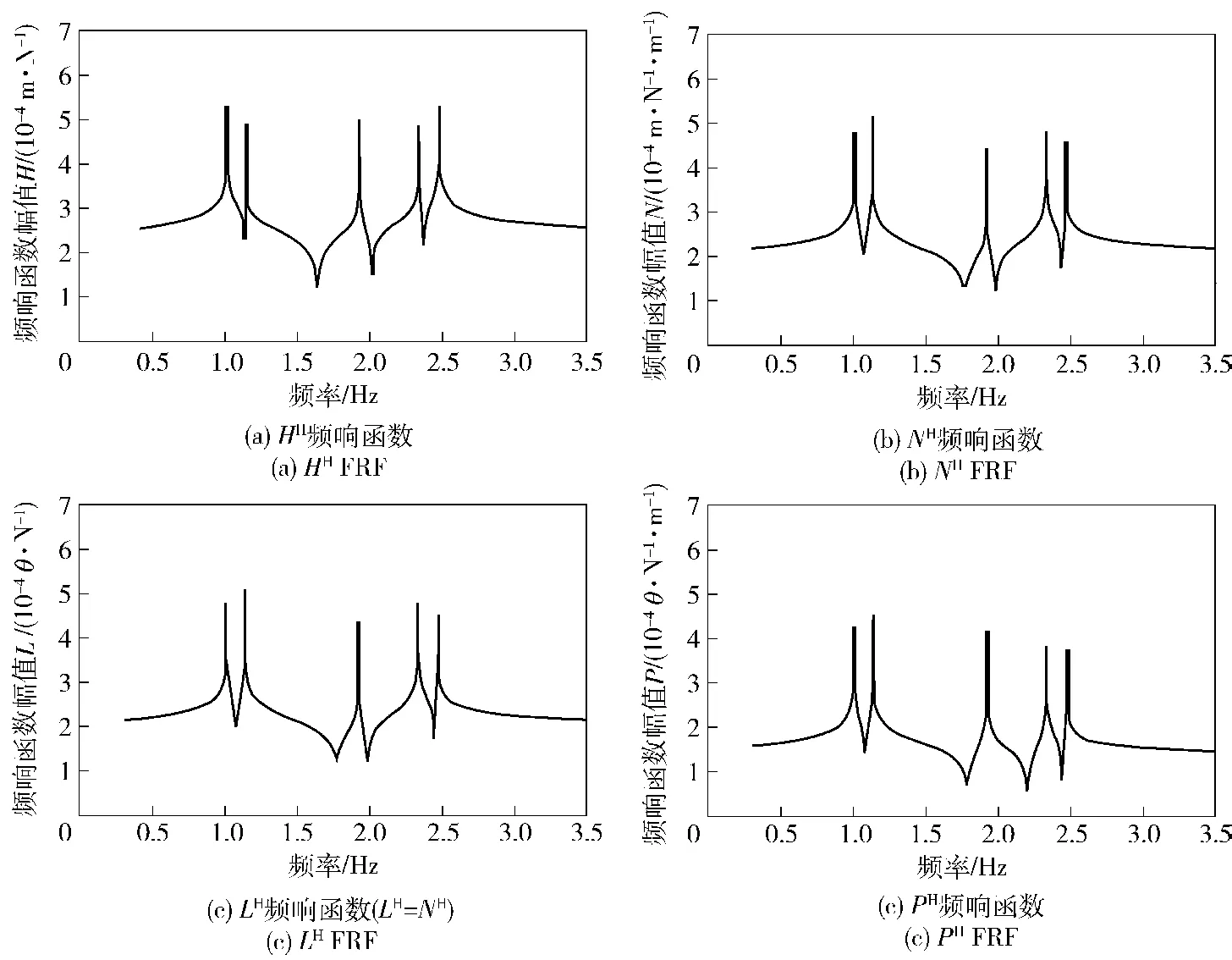
图7 响应矩阵H11的频响函数图Fig.7 FRF of matrix H11

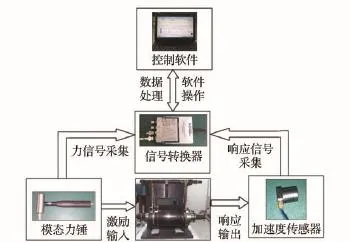
图8 频响函数测量系统图Fig.8 FRF measuring system

2.2.1 HSK主轴端点频响矩阵

以HSK主轴右端为起点，分别将3个加速度传感器按照间隔距离为30 mm直线安装在HSK主轴上，并根据频响函数测量系统，分别测量各个点y方向上的频响函数，图9为端点频响函数.

由图9所示，测量数据存在很多噪声，这会严重影响辨识参数的准确性。因此，本文采用Savitzky-Golay理论对实验数据进行过滤［11］，再用Matlab软件对测量数据重新处理，并将测量的频响函数代入（9）式后插方程中，进而计算得到HSK主轴端点的响应矩阵S11，如图10所示。

图9 HSK主轴端点的频响函数Fig.9 FRF ? of HSK spindle end

2.2.2 HSK主轴-刀柄系统端点频响矩阵

以HSK主轴-刀柄系统右端为起点，分别将3个加速度传感器按照间隔距离为35 mm直线安装在HSK主轴-刀柄系统上，并根据频响函数测量系统，分别测量各个点y方向上的频响函数，并采用相同的方法计算HSK主轴-刀柄系统端点的频响矩阵SH11，如图11所示。

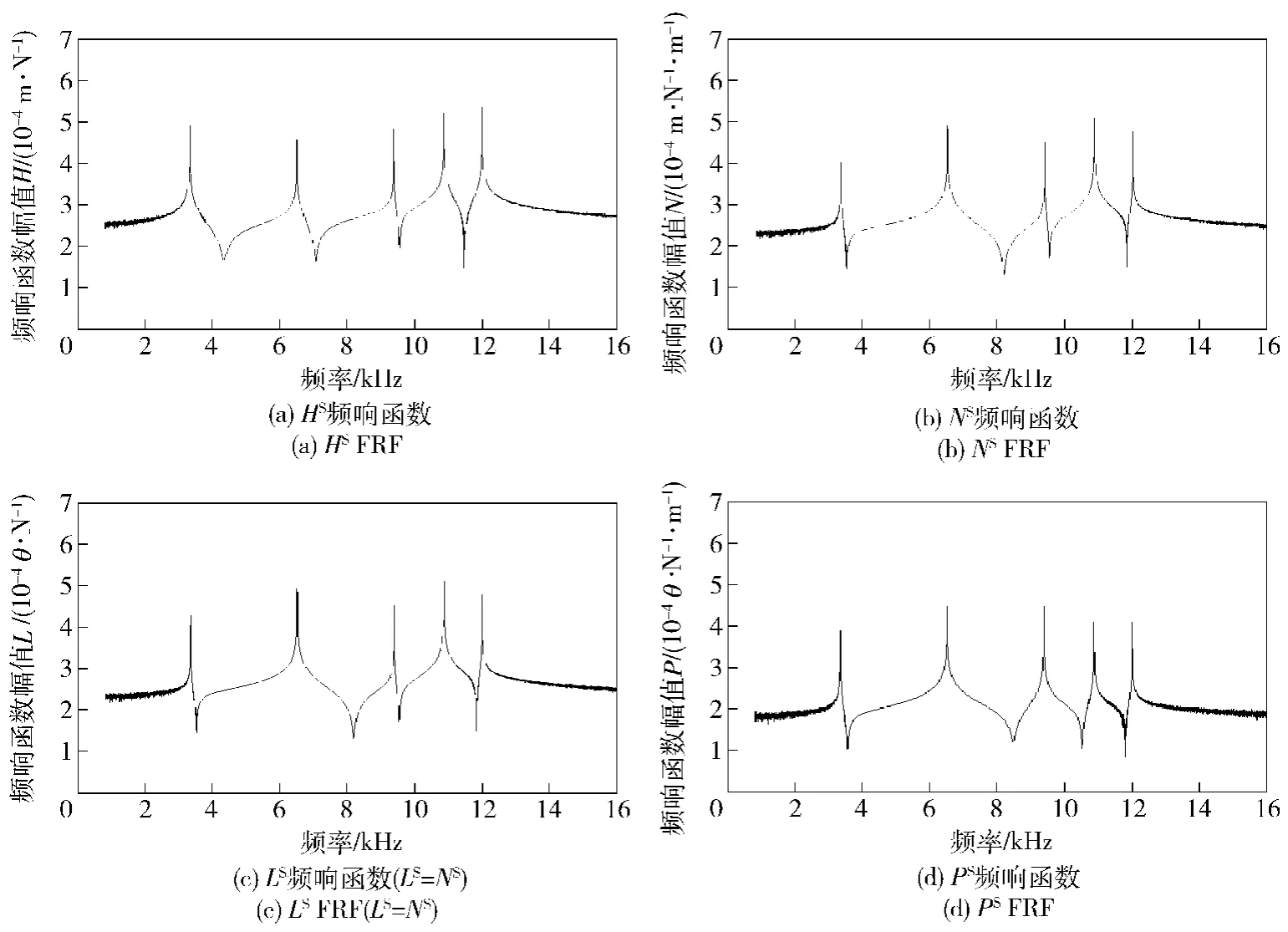
图10 HSK主轴端点的响应矩阵S11Fig.10 FRF matrix S11of HSK spindle end

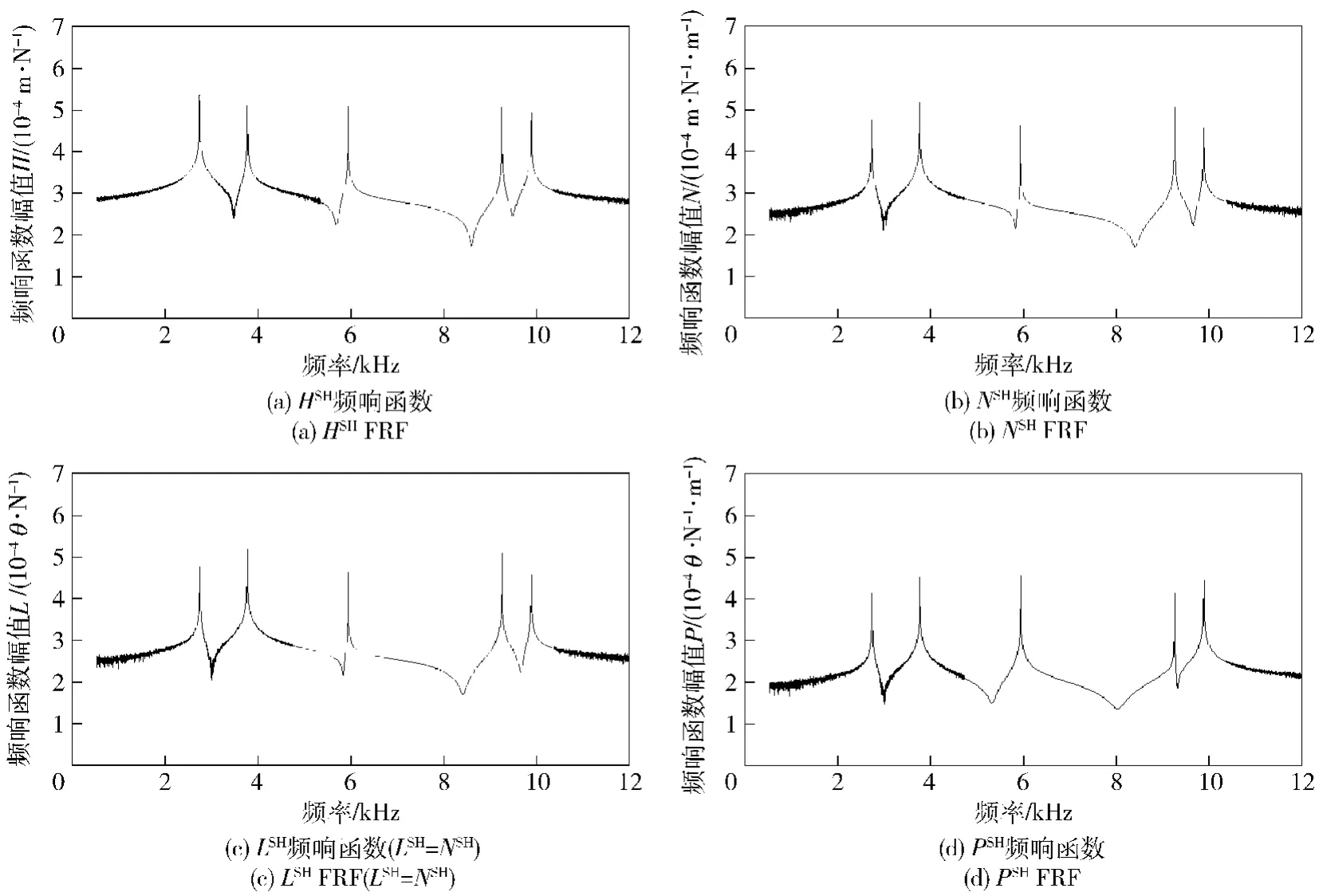
图11 HSK主轴-刀柄系统端点的响应矩阵SH11Fig.11 FRF matrix SH11of HSK spindle-toolholder system end

将所获得的刀柄频响矩阵、HSK主轴端点频响矩阵和HSK主轴-刀柄系统端点频响矩阵代入到（2）式中，便可求得不随频率变化而变化的HSK主轴-刀柄结合部参数，如表2所示。

3 HSK主轴-刀柄结合部参数的验证

本文采用考虑结合部的响应耦合法来计算HSK主轴-热装刀柄的响应矩阵，如（1）式所示。（1）式中，热装刀柄两端频响矩阵和结合部刚度矩阵已经获得，只需将HSK主轴分为多段Timoshenko梁，并根据（10）式～（13）式来计算HSK主轴端点的理论响应矩阵，HSK主轴分段如表3所示。在表1和表3中，刀柄的1～10段和HSK主轴的43～34段形成锥面结合部。由此可得，图12为HSK主轴-刀柄系统端点理论频响函数和实验频响函数

本文使用实验和理论计算的各阶模态相对误差来判定辨识参数和构建模型的准确性［1，12］。因而，将基于耦合响应法计算得到的HSK主轴-热装刀柄系统各阶频率与实验结果相比较，二者最大差值为7.9%，此误差在合理的范围之内，可证明本文所辨识出的HSK主轴-刀柄结合部参数具有一定准确性。并且，采用有限差分法与实验测量相结合的方式，对结合部参数的辨识是可行的。

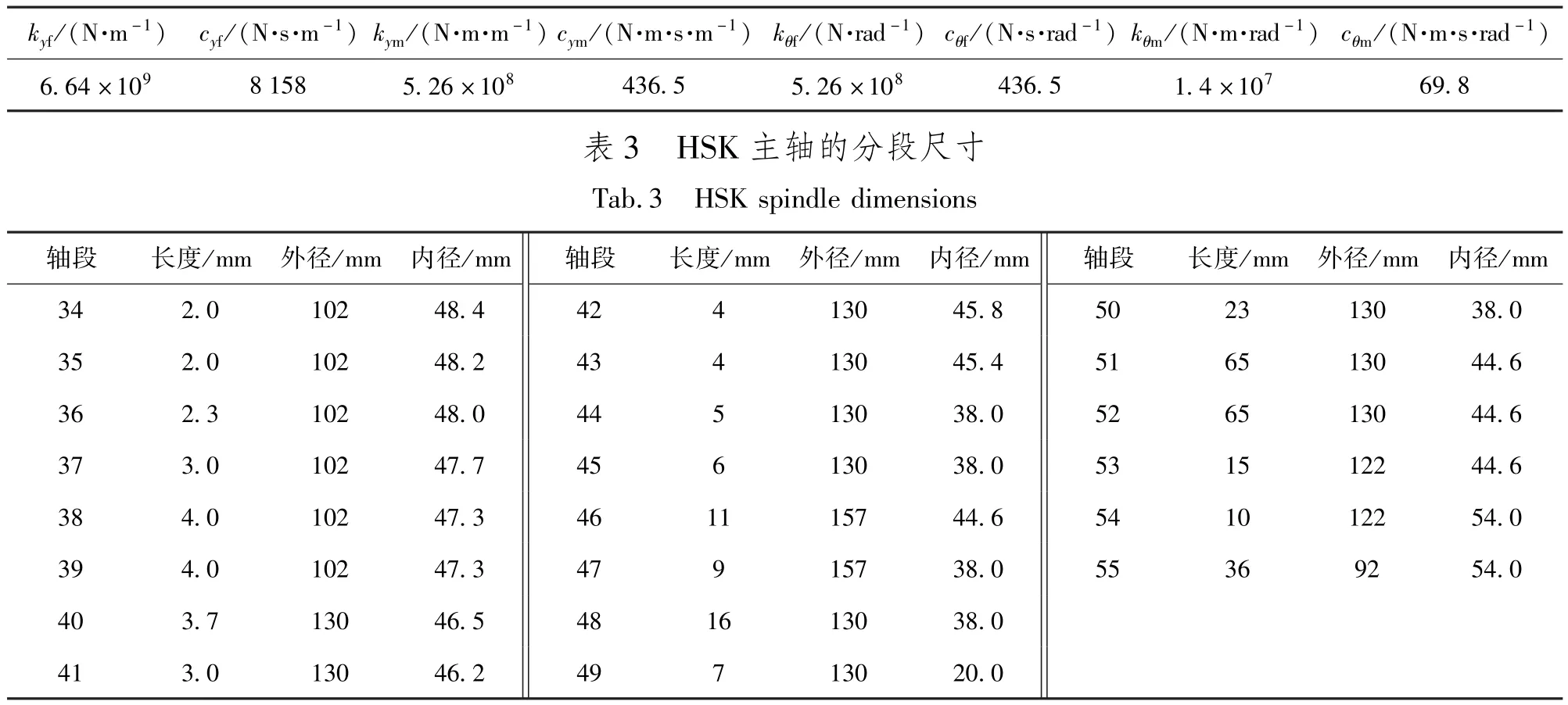
表2 HSK主轴-刀柄结合部参数Tab.2 Joint part parameters of HSK spindle-toolholder

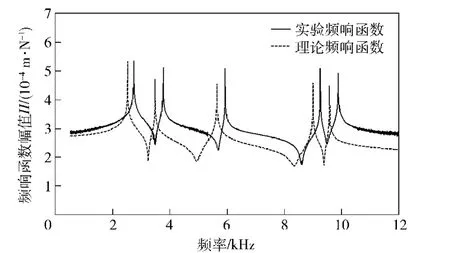
图12 HSK主轴-刀柄系统端点频响函数HSH11Fig.12 FRF HSH11of HSK spindle-toolholder system end

4 结论

1）根据HSK主轴-刀柄系统的响应矩阵公式，推导出HSK主轴-刀柄结合部的刚度矩阵公式。利用耦合响应法计算了热装刀柄的响应矩阵，再采用有限差分与实验测量相结合的方式，分别得到HSK主轴端点和HSK主轴-热装刀柄端点的频响矩阵，并根据刚度矩阵公式，辨识出HSK主轴-刀柄结合部的刚度和阻尼参数。

2）分别使用耦合响应法计算和实验测量，获得HSK主轴-热装系统端点的频响函数，并比较二者的各阶频率，最大差值7.9%，可证明所辨识参数的准确性和辨识方法的可行性。

（

）

［1］ Budak E，Ertürk A，Ozguven H N.Analytical modeling of spindle-tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF［J］. International Journal of Machine Tools&Manufacture，2006，46（15）: 1901-1912.

［2］ Tony L.Schmitz，Kevin Powell，Dongki Won，et al.Shrink fit tool holder connection stiffness/damping modeling for frequency response prediction in milling［J］.International Journal of Machine Tools&Smanufacture，2007，47（9）:1368-1380.

［3］ Namazi M，Altintas Y，Abe T，et al.Modeling and identification of tool holder-spindle interface dynamics［J］.International Journalof Machine Tools&Manufacture，2007，47（9）:1333-1341.

［4］ 程强，刘新宇，赵永胜.基于频响函数的主轴-刀柄结合部参数辨识方法［J］.北京工业大学学报，2013，39（8）:1144-1147. CHENG Qiang，LIU Xin-yu，ZHAO Yong-sheng，Identification of dynamical contact parameters for spindle-tool holder interface based on frequency response functions［J］.Journal of Beijing Technology University，2013，39（8）:1144-1147.（in Chinese）

［5］ Budak E，Ertürk A，Ozguven H N.A modeling approach for analysis and improvement of spindle-holder-tool assembly dynamics［J］.CIRP Annals-Manufacturing Technology，2006，55（1）:369-372.

［6］ Budak E，Ertürk A，Ozguven H N，Effect analysis of bearing and interface dynamics on tool point FRF for chatter stability in machine tools by using a new analytical model for spindle-tool assemblies［J］.International Journal of Machine Tools&Smanufacture，2007，47（1）:23-32.

［7］ Özsahin O，Erturk A，Özguven H N，et al.A closed-form approach for identification of dynamical contact parameters in spindle-holder-tool assemblies.［J］.International Journal of Machine Tools&Smanufacture，2009，49（1）:25-35.

［8］ Schmitz T L，Duncan G S.Receptance coupling for dynamics prediction of assemblies with coincident neutral axes［J］.Journal of Sound&Vibration，2006，289（4/5）:1045-1065.

［9］ Duarte M L M，Ewins D J.Rotational degrees of freedom for structural coupling analysis via finite-difference technique with residual compensation［J］.Mechanical Systems&Signal Processing，2000，14（2）:205-227.

［10］ 王贵成，王树林，董广强.高速加工工具系统［M］.北京:国防工业出版社，2005. WANG Gui-cheng，WANG Shu-lin，DONG Guang-qiang.Tooling system for high speed machining［M］.Beijing:National Defense Industry Press，2005.（in Chinese）

［11］ Savitzky A，Golay M J E，Chem A.Smoothing and differentiation of data by simplified least squares procedures［J］.Analytical Chemistry，1964，36（8）:1627-1639.

［12］ 汪博，孙伟，闻邦椿，考虑主轴-刀柄-刀具结合面的高速主轴系统动力学特性有限元建模［J］.机械工程学报，2012，48（15）:83-89. WANG Bo，SUN Wei，WEN Bang-chun.The finite element modeling of high-speed spindle system dynamics with spindleholder-tool Joints［J］.Journal of Mechanical Engineering，2012，48（15）:83-89.（in Chinese）

Identification of Joint Part Parameters of HSK Spindle-toolholder Based on Closed-form Approach

CHEN Jian1，TIAN Liang2，SHANG Hong-mo2，ZHENG Deng-sheng1，WANG Gui-cheng1，3
（1.School of Mechanical Engineering，Jiangsu University，Zhenjiang 212013，Jiangsu，China；2.Chengdu tool research institute Co.，LTD，Chengdu 610051，Sichuan，China；3.Nantong Polytechnic College，Nantong 226002，Jiangsu，China）

The basic condition for predicting the dynamic performance of spindle system and keeping the cutting stability is to identify the parameters of HSK spindle-toolholder joint part.HSK spindle-toolholder joint part is simplified as spring-damp model.According to the frequency response function（FRF）matrix of HSK spindle-shrink toolholder system，the stiffness matrix of HSK spindle-toolholder is derived.the FRF matrix of shrink toolholder is obtained based on coupling response method.The FRF matrixes of the tip points of HSK spindle and HSK spindle-shrink toolholder system are got by using finite difference method and experiment.Four stiffness parameters（kyf，kθf，kymand kθm）and four damp parameters（cyf，cθf，cymand cθm）are identified with the stiffness matrix.FRF of tip point of HSK spindle-toolholder sys-tem is achieved by using the coupling response method.The calculated frequency of HSK spindle-toolholder system is compared with the experimental frequency.The maximal difference between theoretical and experimental results is 7.9%.

manufaturing technology and equipment；HSK spindle-toolholder joint part；FRF matrix；parameter identification

TG504

A

1000-1093（2015）07-1309-09

10.3969/j.issn.1000-1093.2015.07.021

2014-09-19

国家自然科学基金项目（51075192、51275217）；国家重大科技专项（2013ZX04009031）；南通市重点实验室资助项目（CP12014002）；江苏省博士创新基金项目（CXZZ13_0656）

陈建（1987—），男，博士研究生。E-mail:jiangsuxuezi@163.com；王贵成（1955—），男，教授，博士生导师。E-mail:wgch@ujs.edu.cn