液压油体积弹性模量稳态模型与动态模型的对比

魏超，周俊杰，苑士华

（北京理工大学车辆传动国家重点实验室，北京100081）

液压油体积弹性模量稳态模型与动态模型的对比

魏超，周俊杰，苑士华

（北京理工大学车辆传动国家重点实验室，北京100081）

油液体积弹性模量对液压系统的动态特性有着重要影响，而现有模型尚无法准确反映油液压缩与膨胀过程的动态特性。引用分析了4种基于集中参数法的液压油有效体积弹性模量的稳态模型（Wylie模型、Nykanen模型、Ruan模型和AMESim模型），结合空气和蒸汽的动态传输方程，推导得到了考虑含气量时变特征的有效体积弹性模量动态模型。在此基础上，分析了4种稳态模型分别在高压区和低压区的变化特性，研究了AMESim模型和动态模型稳态值的差异性，验证了动态模型的有效性。研究表明：由于假设含气量不变，Wylie模型、Nykanen模型在全压力范围内差别很小；高压时Ruan模型计算结果稍大，而AMESim模型计算曲线较为特殊，受空气分离压影响很大；低压时Ruan模型、Wylie模型计算结果非常接近，而当压力低于饱和蒸汽压时AMESim模型计算值约为0.在应用Henry定律条件下，动态模型预测的体积弹性模量-压力曲线更为合理。油液压缩膨胀循环实验表明动态模型具有更高的精度。

兵器科学与技术；有效体积弹性模量；液压油；含气量；动态模型

0 引言

液压油的可压缩性对液压系统的动态特性有着重要影响，精确的体积弹性模量模型成为该领域研究人员一直追求的目标［1］。液压油的体积弹性模型与油的含气率有着密切关系，高压时油的含气率较低，因此高压下的体积弹性模量模型相对较为成熟［2］。但是低压时，伴随着空气分离和油液汽化等空化现象的发生，液压油的压缩特性变得非常复杂，同时由于液压元件（如液压泵、马达、阀等）中存在着大量低压或高、低压过渡区域，在这些区域中低压油液的弹性模型对元件的动态响应有着巨大影响［3-4］。因此，低压油液体积弹性模量的计算成为当前液压油参数模型研究的难点与重点［5］。

目前，液压油的参数模型可大体分为两类:一类是基于界面追踪两相流假设的参数模型，另一类是基于集中参数连续体假设的参数模型［3］。界面追踪模型对流体组分分别研究，各相通过传输方程互相联系，从微观角度出发力求对各相之间的分界面进行准确描述。目前，这类流体模型多被计算流体力学（CFD）仿真技术采用［6-8］，运用这种方法，有利于得到流场空化现象的细节，适合于复杂流场分析，但是建模复杂，计算量大。耦合空化模型的集中参数建模方法从宏观角度出发，假设流体性质均匀分布，重点研究液压油内蒸汽和自由空气的比重，这种方法可以大幅减少方程个数，提高数值计算速度和效率。考虑到液压系统的仿真和研究中人们的关注重点在于元件性能和系统表现而不是流场细节，因此选择第2种方法能更方便、快捷地满足需求。基于此，研究人员发展了针对液压系统的液压油参数模型并进行了各种应用［9-14］，值得提出的是，液压系统仿真软件LMS.AMESim也是应用集中参数模型［15］。

根据是否考虑含气率随油液压力的变化特性，集中参数模型对油液体积弹性模量的计算可归类为两种［16］:一是认为液压油内含气量为常数，二是假设含气量随压力呈单参数变化关系。前者假设含气量在全压力范围内保持不变，例如文献［9-10］提出的模型；后者多应用Henry定律描述平衡状态下含气量随油液压力变化的关系，如文献［15］。但是，这些模型都没有考虑油液中含气量随各种因素变化的时间效应，忽略了气相在油液中处于非平衡态时发生的动态传输过程。因此，现有的液压油有效体积弹性模量模型（本文称为稳态模型）还不能完全描述油液中气相的时变特征。近来，Manhartsgruber［17］、Schran等［18］对液压油内气体的析出和消解过程进行了实验研究，发现压力和容积变化率对空气的析出和消解速率有明显影响；文献［19］以Full Cavitation Model为理论基础建立了油液内气体的动态传输方程。基于以上原因，为满足液压系统高精度、快响应的发展要求，本文通过定义法推导了液压油体积弹性模量的动态模型，并通过与实验结果以及稳态模型的对比分析证明了新模型的有效性。

1 有效体积弹性模量

液压油在一定压力作用下体积减小表现出可压缩性，有效体积弹性模量表示了液压油实际工作过程中压缩特性，其定义为

式中:p为油液工作压力；V为油液体积。

液压油的有效体积弹性模量主要受油液工作压力、温度以及含气量的影响。通常情况下纯油的体积弹性模量随压力的升高而增大，而随温度的升高则减小，但幅度都很小。因此纯油体积弹性模量与压力和温度的关系［14］可简化为

式中:Eref为纯油液在标准压力温度下的体积模量；Δp为油液工作压力；ΔT为温度的变化值；m为体积弹性模量的压变系数；n为温变系数。

2 稳态模型

常用的油液有效体积弹性模量模型主要有4种:Wylie模型、Nykanen模型、Ruan模型以及AMESim模型，其中Wylie模型、Nykanen模型均假设油液的含气量为常数，Ruan模型考虑了压力对含气量的影响，而AMESim模型认为含气量是油液压力的单参数函数（基于Henry定律）。各模型表达式如下:

1）Wylie模型［9］

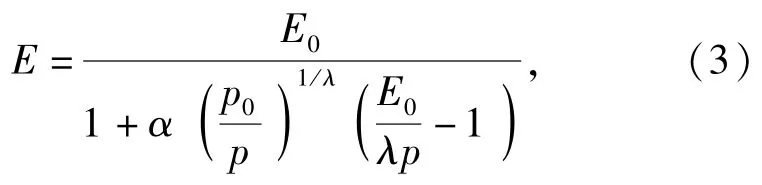
式中:E0为大气压力下液压纯油液的体积模量；α为油液的空气含量；p0为一个标准大气压；λ为空气的热容比。

2）Nykanen模型［10］

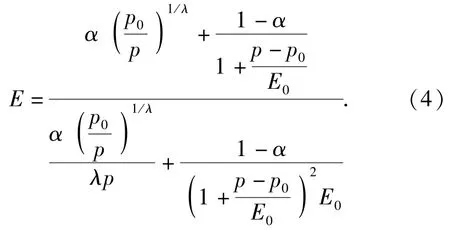
3）Ruan模型［12］

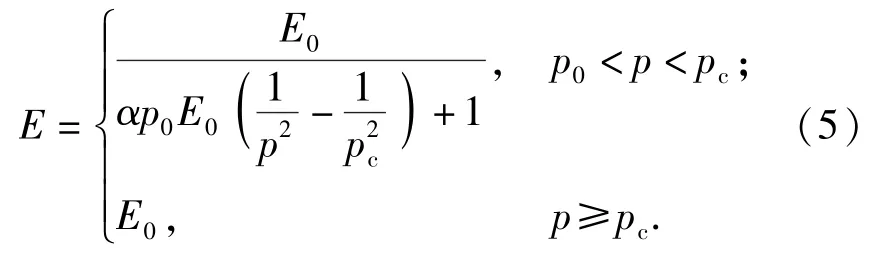
式中:pc为临界压力。

4）AMESim模型［15］

式中:θ为液压油内空气析出比例；φ为液压油内蒸汽的析出比例（θ和φ与油液压力相关）；ρL为纯油液密度；C1=（1-α）ρL0，ρL0为1个标准大气压下纯油液密度；，ρv为油蒸汽在饱和蒸汽压力pv下的密度。同时，AMESim模型将流体介质细分为液体-空气-蒸汽混合的3成分4状态（如图1所示）:①当油液内部压力高于空气分离压力ps时，空气完全溶解在油液中，表现为纯液体状态；②当油液内部压力低于空气分离压力时，空气开始析出直到建立起新的溶解平衡态；③当油液压力继续降低到饱和蒸汽压力pv以下，此时油液开始汽化发生相变产生油蒸汽，油液内将包含空气和蒸汽两种气相；④如果继续减小压力至完全汽化压力pf，则油液将完全汽化，液态消失而将成为空气和蒸汽的气态混合物。

另外，针对图1第2种和第3种状态中含有部分空气和部分蒸汽的情况，要根据（6）式计算油液的有效体积弹性模量，前提是必须根据压力确定液压油内空气和蒸汽的析出比例θ和φ.Henry定律描述液体能溶解的空气量和液体内部压力呈正比例关系，而压力降低时析出的空气比例θ负比例相关于压力，图2中虚直线表示了这一关系。但（6）式中dθ/dp如果按图2虚线计算则其值在两端压力上不连续，因此，AMESim模型引入了θ-p的二次插值函数［15］，如图2中实线所示，旨在保证（6）式中θ对压力导数的数值稳定性，同样（6）式中dφ/dp也作了相似的处理，不同的是φ-p是分布在饱和蒸汽压力pv和完全汽化压力pf之间的函数。

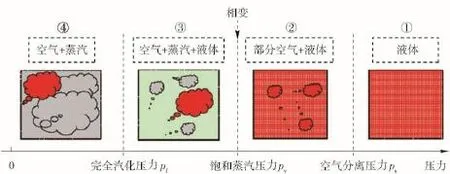
图1 AMESim液体-空气-蒸汽液压油模型Fig.1 AMESim hydraulic oil model for liquid-air-vapour

3 动态模型

由于油液中通常含有空气，因此油液的压缩性主要来源于压力变化引起的液体体积改变和气体体积改变。而在特殊条件下，油液中可能还含有油蒸汽，此时液压介质将成为由纯油液、空气以及油蒸汽3种成分组成的两相混合物。考虑到油液中气体较少，散布在油液中，气体之间的互相影响较弱，并且气体与周围液体间渗透作用很小，因此可认为纯油液、空气和蒸汽这3种成分受压时的体积改变互相独立，并随时间变化，则流体的有效体积弹性模量可由（1）式变形得

式中:VL为油液混合物中纯液体的体积；Vg为油液混合物中空气体积；Vv为油液混合物中油蒸汽的体积。它们都可以视为以时间为变量的函数。

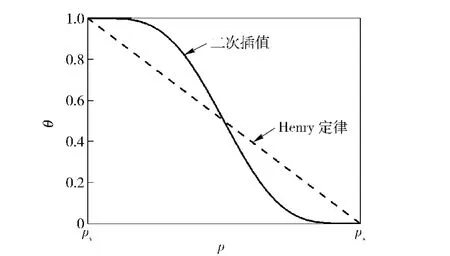
图2 AMESim模型含气量的计算Fig.2 Air content calculation of AMESim model

假设αg、αv为空气和蒸汽在瞬时压力下的体积分数，则它们和质量分数fg和fv存在如下关系:

式中:ρg为油液空气的密度；ρ为混合物的平均密度。

针对（7）式中的气体成分应用气体压缩方程，设Vg0与Vv0为空气和蒸汽在标准大气压p0下的体积，则有

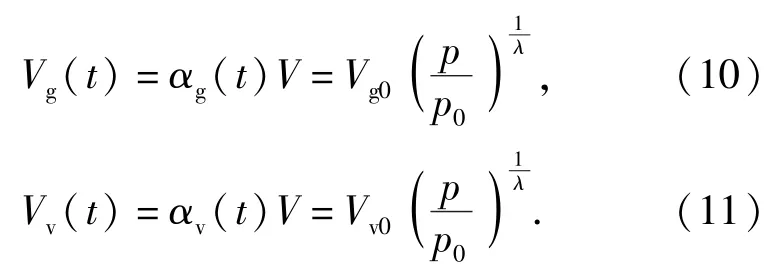
而纯油液的体积由以下表达式［20］给出:

式中:VL0为纯油液在标准大气压p0下的体积。

分别对（10）式～（12）式求关于压力p的导数，并代入（7）式整理，可得弹性模量动态模型

由（13）式可知，体积弹性模型与空气和蒸汽的质量分数fg（t）、fv（t）有关，根据参考文献［19］，fg（t）、fv（t）可通过求解空气和蒸汽的动态传输方程（14）式、（15）式得到。

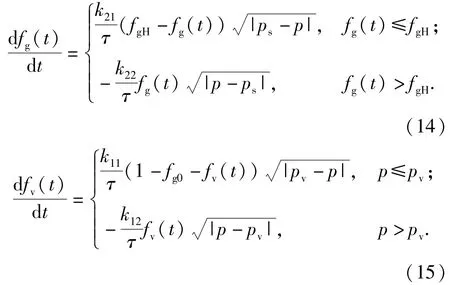
（14）式和（15）式中:fgH表示空气含气率的稳态值；fg0为油液内空气的初始含量；k21、k22、k11、k12为经验系数。可以看出，（14）式和（15）式代表了空气析出和油液汽化两个动态过程，同时还可看出，含气量变化率不仅和压力有关，还受油液内当前含气量、特征时间子以及其他经验系数等诸多因素影响，而且空气分离压力ps和饱和蒸汽压力pv是两个分别影响空气和蒸汽含量的关键压力。通过对气体传输方程的求解，可以准确得知液压油内含气量。结合（13）式，便可精确计算出流体的有效体积弹性模量。此外，动态模型省去了AMESim模型中人为给定的含气量插值函数，更接近实际情况，虽引入了未知的空气和蒸汽的质量分数fg（t）和fv（t），但同时也引入了描述二者内部传输过程的两个常微分方程，因此不会影响系统方程组的封闭性。

另外，由稳态关系dfg/dt=0可知，此时fg（t）= fgH.并且稳态值fgH可以完全按照Henry定律设定的与油液压力呈现的正比例关系，即（16）式，来进行计算，其中fg0为油液内空气的初始含量。

此时，动态模型退化为类似于AMESim模型的稳态模型。

4 对比分析

为分析以上模型的差异，通过一仿真算例进行说明。仿真中采用液压油的基本参数见表1，计算得到的有效体积弹性模量如图3、图4和图5.

表1 液压油基本参数Tab.1 Basic parameters of hydraulic oil

图3给出了高压范围液压油有效体积弹性模量4个稳态模型的比较结果。由图3可见，由于Wylie模型和Nykanen模型均认为液压油内含气率α在整个压力范围内保持不变，忽略了压力对液压油溶解度的影响。因此，Wylie模型和Nykanen模型计算结果差别很小，只是在压力超过100 bar时，Nykanen模型计算结果稍大。另外，Ruan模型计算值稍大于Wylie模型和Nykanen模型，这是由于模型考虑了压力升高后部分气体溶解在液体内的影响，由（5）式不难看出，当压力达到或超过临界压力pc时，Ruan模型认为油液中气体已经消失，有效体积弹性模量即为E0.当压力接近pc时，有效体积弹性模量也趋近于E0，相当于油液内含气量在逐渐降低。从图3还可看出，AMESim模型与其他3种模型之间差距明显，体积弹性模量的增长曲线不如前者平顺，形状较为特殊，原因是AMESim模型对（6）式中dθ/dp和dφ/dp的数学处理虽然能保证求导的数值稳定，但却使得导数值随压力变化比较剧烈，并最终反映在体积弹性模量变化曲线上。并且，图3还显示，空气分离压力ps的取值对AMESim模型的计算结果影响很大（ps值一般通过实验确定［5］）。

图4给出了低压范围液压油有效体积弹性模量4个稳态模型的比较结果。从中可以看出，低压区Wylie模型和Nykanen模型仍然比较接近，并且此时Ruan模型计算结果几乎和Wylie模型一样。由于前3种模型都忽略了油液的汽化现象，而实际上当压力低于饱和蒸汽压力时油液会发生汽化，因此，在压力下降到饱和蒸汽压力pv以下后，AMESim模型的计算结果不同于前3个，而是呈现为迅速降低至0.显然，低压时AMESim模型与实际情况更为接近，故其计算结果比前3种模型的计算精确性要高。

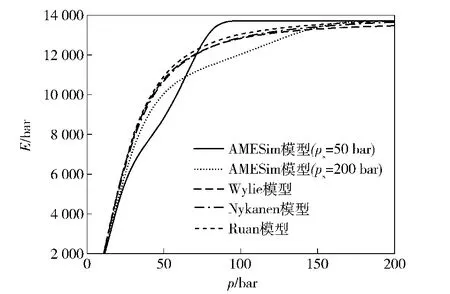
图3 液压油有效体积弹性模量稳态模型比较（高压范围）Fig.3 Steady-state models of effective bulk modulus（high pressure）

图4 液压油有效体积弹性模量稳态模型比较（低压范围）Fig.4 Steady-state models of effective bulk modulus（low pressure）

图5 AMESim模型和动态模型比较Fig.5 Comparison of AMESim model and dynamic model

图5为AMESim模型和动态模型稳态值的对比曲线。从中可以看出，动态模型和AMESim模型的区别主要体现在空气分离压力之前，动态模型预测的有效体积弹性模量-压力曲线形状更为平顺，这是由于动态模型中空气析出含量是由（16）式线性关系确定而不是AMESim模型的二次插值函数，因此消除了含气量变化速率dθ/dp剧烈变化对体积弹性模量带来的影响。并且，通过对比（13）式和（6）式可知，这两式的主要区别在于（6）式分母中多出了dθ/dp和dφ/dp两项，同时由图2的θ-p曲线可以看出，dθ/dp为负值（同理dφ/dp也为负值），因此其使得（6）式的分母增大，故而AMESim模型的计算值要小于动态模型的稳态值。

显然，以上稳态模型均无法反映空气析出和油液汽化的动态过程，在压力变化迅速的液压系统中，很多时候油液是来不及建立或达到这一平衡状态的，因此考虑含气量在非平衡态下的时变特征是非常必要的。

5 实验验证

为检验动态模型的有效性，与奥地利Johannes Kepler大学Manhartsgruber教授进行了合作研究。Manhartsgruber教授研究组针对本文的动态模型开展了液压油有效体积弹性模量的模型实验。如图6所示，实验采用的密闭油缸内装有含一定空气的液压油，通过压力传感器和热电偶分别获取油腔内油液的压力和温度。被测油缸底部活塞的位置可以由伺服系统精确控制，以此实现油缸内液压油的压缩与膨胀循环。循环由低压开始，低压到高压为压缩行程，高压到低压为膨胀行程。实验用液压油为标准型ISO 32矿物油，其主要属性与实验参数如表2所示，为保证一致仿真模型中油液的各项属性按实际给定。

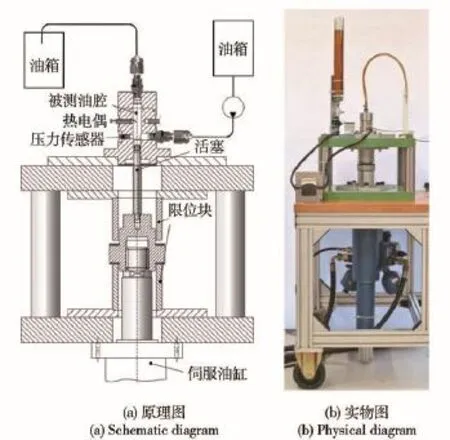
图6 油液体积弹性模量实验台原理Fig.6 Principle of fluid bulk modulus testbed

表2 实验和仿真参数Tab.2 Experimental and simulation parameters

需要说明的是，受限于实验台伺服缸控制与被测油室不发生变形的要求，实验中测试油液压力不能太高，被限定在0～32 bar之间。图7所示的对比结果表明，动态模型很好地吻合了实验数据，并能准确预测出压缩膨胀循环过程中液压油有效体积弹性模量表现出的“迟滞”特性。产生这一现象的具体原因是:循环开始时油液低于空气分离压力ps，并含有一定量析出的自由空气，压缩行程中析出的空气随压力升高溶于油液，但溶解速率较慢；转为膨胀行程时，油缸压力降低，但仍高于空气分离压力，故而空气继续溶解，直至油液压力低于空气分离压力；当压力低于空气分离压力后，已经溶解的空气反过来迅速析出，因析出速率比溶解速率大很多，所以油液内气体含量很快回到循环前的初始值，形成一个循环周期。与空气分离压力的对比决定循环过程中大部分时间内空气在溶解，这导致在压缩和膨胀行程中油液含气率不同，表现为压缩行程多而膨胀行程少，从而油液的有效体积弹性模量将不在一条曲线，表现出图7的“迟滞”特征。另外，图7也给出了压缩膨胀过程中的稳态模型解。从中可以看出，稳态模型得到的油液体积弹性模量是一条曲线，无法反映“迟滞”现象，对比实验值误差较大。

图7 动态模型的实验验证（循环周期1 s）Fig.7 Experimental verification of dynamic model（circle time of 1 s）

6 结论

1）对比了4种基于集中参数法的液压油有效体积弹性模量的稳态模型，计算表明:高压时Wylie模型、Nykanen模型差别很小；Ruan模型因考虑压力升高含气率降低的影响使得计算结果稍大；AMESim模型计算曲线相比其他3种稳态模型形状较为特殊，差别较大，并且受空气分离压力ps的影响很大。低压时Wylie模型、Nykanen模型及Ruan模型差别不明显，当压力低于饱和蒸汽压时，由于AMESim模型考虑了油液汽化现象，因此其预测的有效体积弹性模量很小，约为0.

2）由定义法推导了液压油有效体积弹性模量的动态模型，其预测的有效体积弹性模量-压力曲线相比AMESim模型更为平顺，在空气分离压力之前AMESim模型计算值偏低。此外，动态模型可以通过耦合气体传输方程考虑含气量变化的时变特征。

3）实验表明，动态模型的仿真结果能反映出油液压缩膨胀循环中体积弹性模量值的“迟滞”特性，而稳态模型无法反映该现象。因此，动态模型相比稳态模型具有更高的计算精度。

（

）

［1］ 李松年，葛思华，史维祥.油液体积弹性模量βe的在线测量技术［J］.机械工程学报，1989，25（3）:89-96. LI Song-nian，GE Si-hua，SHI Wei-xiang.The technique for the on-line measurement of the bulk modulus of hydraulic fluid βe［J］. Journal of Mechanical Engineering，1989，25（3）:89-96.（in Chinese）

［2］ Munson B，Young D.Fundamentals of fluid mechanics［M］.New York，US:John Wiley&Sons Incorporation，2002.

［3］ Vacca A，Klop R，Ivantysynova M.A numerical approach for the evaluation of the effects of air release and vapour cavitation on effective flow rate of axial piston machines［J］.International Journal of Fluid Power，2010，11（1）:33-46.

［4］ 徐巨华.油液体积弹性模量对电液伺服系统动态特性影响研究［D］.杭州:浙江大学，2013. XU Ju-hua.Research on dynamic characteristics of servo system with oil bulk modulus［D］.Hangzhou:Zhejiang University，2013.（in Chinese）

［5］ Gholizadeh H，Burton R，Schoenau G.Fluid bulk modulus:a literature survey［J］.International Journal of Fluid Power，2011，12（3）:5-16.

［6］ Shimada M，Nozaki S，Kobayashi T，et al.Numerical study of the cloud cavitation in a fuel injection pump［R］.New York，US: SAE，1998.

［7］ 张健，方杰，范波芹.VOF方法理论与应用综述［J］.水利水电科技进展，2005，25（2）:67-70. ZHANG Jian，FANG Jie，FAN Bo-qin.Advances in research of VOF method［J］.Advances in Science and Technology of Water Resources，2005，25（2）:67-70.（in Chinese）

［8］ Singhal K，Athavale M，Li H，et al.Mathematical basis and validation of the full cavitation model［J］.Journal of Fluids Engineering，2002，124（3）:617-624.

［9］ Wylie M，Streeter L.Fluid transient［M］.Ann Arbor，Michigan，US:Michigan University Press，1978.

［10］ Nykanen J.Comparison of different fluid models［C］∥Bath Workshop on Power Transmission and Motion Control.Bath，UK: University of Bath，2000:101-110.

［11］ Casoli P，Vacca A，Franzoni G，et al.Modelling of fluid properties in hydraulic positive displacement machines［J］.Simulation Modelling Practice and Theory，2006，14（8）:1059-1072.

［12］ Ruan J.Bulk modulus of air content oil in a hydraulic cylinder［C］∥Proceedings of the 2006 ASME International Mechanical Engineering Congress and Exposition.Chicago，IL:ASME，2006: 259-269.

［13］ Haas R.Compressibility measurements of hydraulic fluids in the low pressure range［C］∥Proceedings of the 6th FPNI PhD Symposium.West Lafayette，IN:Purdue University，2010:681-690.

［14］ Kim S，Murrenhoff H.Measurement of effective bulk modulus for hydraulic oil at low pressure［J］.Journal of Fluids Engineering，2012，134（2）:1-10.

［15］ Imagine S A.HYD advanced fluid properties［EB/OL］.［2014-07-15］.http:∥www.plm.automation.siemens.com/zh_cn/ products/lms/imagine-lab/amesim/.

［16］ Gholizadeh H，Burton R，Schoenau G.Fluid bulk modulus:comparison of low pressure models［J］.International Journal of Fluid Power，2012，13（1）:7-16.

［17］ Manhartsgruber B.Experimental results on air release and absorption in hydraulic oil［C］∥Proceedings of the ASME/BATH Symposium on Fluid Power&Motion Control.Bath，UK:University of Bath，2013.

［18］ Schrank K，Murrenhoff H.Measurements of air absorption and air release characteristics［C］∥Proceedings of the ASME/BATH Symposium on Fluid Power&Motion Control.Bath，UK:University of Bath，2013.

［19］ Zhou J，Vacca A，Manhartsgruber B.A novel approach for the prediction of dynamic features of air release and absorption in hydraulic oils［J］.Journal of Fluids Engineering，2013，135（9）: 091305.

［20］ Kundu P，Cohen I，Dowling D.Fluid mechanics［M］.Amsterdam，Netherlands:Elsevier Incorporation，2004.

Comparison of Steady and Dynamic Models for the Bulk Modulus of Hydraulic Oils

WEI Chao，ZHOU Jun-jie，YUAN Shi-hua
（Science and Technology on Vehicle Transmission Laboratory，Beijing Institute of Technology，Beijing 100081，China）

Fluid bulk modulus has important effect on the dynamic characteristics of the hydraulic system，but the existing models still cannot accurately capture the dynamic features when the fluid is compressed or expands rapidly.Four steady-state models（Wylie，Nykanen，Ruan and AMESim）of fluid bulk modulus based on lumped parameter approach are analyzed.Considering the dynamic transport processes of free air and vapor in the oil，a dynamic effective bulk modulus model which is time-dependent is derived.In addition，the difference among the four steady-state models both in the high and low pressure regions is studied.The proposed dynamic model is compared to AMESim model and validated using experimental data.Results show that Wylie model is close to Nykanen model in the whole pressure range since they both assume constant air contents.In the high pressure region，Ruan model predicts a slight larger fluid bulk modulus，while AMESim model performs most differently and is strongly affected by the air apart pressure.In the low pressure region，the values of Ruan Model and Wylie Model are very close，but the effective bulk modulus calculated by AMESim model is nearly zero when the pressure islower than the vapor saturation pressure，the fluid bulk modulus-pressure curve—predicted by the proposed dynamic model seems more reasonable when Henry's law is used，although its advantage depends on the coupling with the dynamic transport equations.Finally，the comparison of the results obtained from a fluid compression and expansion test cycle indicates that the proposed model is more precise.

ordnance science and technology；effective bulk modulus；hydraulic oil；air content；dynamic model

TH137

A

1000-1093（2015）07-1153-07

10.3969/j.issn.1000-1093.2015.07.001

2014-09-28

国家自然科学基金项目（51175039）

魏超（1980—），男，副教授。E-mail:weipeter1@bit.edu.cn；周俊杰（1986—），男，讲师。E-mail:121zhouxiao@163.com