基于MSC/NASTRAN的小水线面双体船结构优化设计研究

魏 刚

（上海交通大学 船舶海洋与建筑工程学院 上海 200030）

基于MSC/NASTRAN的小水线面双体船结构优化设计研究

魏 刚

（上海交通大学 船舶海洋与建筑工程学院 上海 200030）

该文对NASTRAN的最新结构优化方法和结构优化流程作了介绍， 阐述了NASTRAN一般结构优化的数学模型和拓扑优化的物理模型。以小水线面双体船的舱段模型为研究对象，首先以提高舱段结构的整体刚度为目标进行拓扑优化、形状优化和尺寸优化，进而结合工程适用性提出贴近优化结果的可行优化设计，最后通过有限元直接计算比较验证了优化方案相对常规设计的结构响应的改善。

小水线双体船；结构优化设计；横向强度

引 言

小水线面双体船是一种性能优良的新船型，型宽较大，在减小船舶横摇幅度的同时还为舱室布置提供宽阔的空间。然而，型宽较大也使小水线面双体船的结构质量占空船质量的比重偏大，因而，如何在保证结构安全的前提下合理分配和控制结构质量，已成为该类船型结构设计的关键。

结构优化在飞机、汽车及船舶等结构设计中变得越来越重要，结构优化设计是运筹学在工程设计上的实用，特别适于解决稀缺资源的优化分配问题［1］。结构优化的目标是寻求结构各设计参数的最优解，使该结构成本最小且能满足一系列设计要求［2］。作为一款通用的有限元计算软件，MSC/NASTRAN在结构优化设计方面也具有强大的功能。本文以小水线面双体船的一个舱段为研究对象，单独及组合使用MSC/NASTRAN的各类优化方法，结合结构有限元直接计算分析对小水线面双体船的主要结构进行优化设计。

1 基于Msc/Nastran的结构优化方法

NASTRAN的优化算法是基于梯度的方法［3］，它利用梯度信息进行数值优化解的搜素。由于在实际结构优化当中，设计域内的目标响应是隐性的，需用有限元直接计算才能得到，且设计变量和设计约束也非常多，这样就造成无法接受的计算成本。NASTRAN通过变量连接、约束筛选、工况删除以及标准化近似等一系列技术建立近似设计模型来解决这个问题。

NASTRAN的优化功能分一般优化设计和拓扑优化设计，一般优化设计可完成尺寸优化和形状优化等优化任务，而拓扑优化专门用来研究材料的优化布置。

1.1 Nastran的一般结构优化方法

NASTRAN中结构优化设计问题的数学模型可表述为求使目标函数F（X）最小或最大的X，其中X=｛x1，x2，…xn｝，还要满足以下约束：

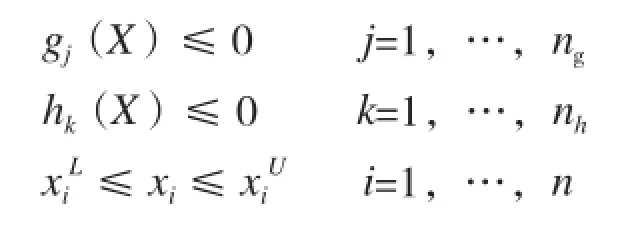
目标函数只能是单一的标量函数，目标和约束函数关于设计变量可以是线性的也可以是非线性的。有了优化问题的数学表达，NASTRAN会根据实际结构优化问题的特点自动选择优化器和优化算法，NASTRAN目前集成MSCADS和IPOPT两个优化器。MSCADS优化器包含改进的可行方向法［4］、序列线性规划法［5］、序列二次规划法［6］以及序列无约束极小化技术［7］等一系列优化算法可供NASTRAN或用户依具体结构优化问题的特点进行选择。IPOPT优化器应用线性搜索过滤内点算法［8］寻求大规模非线性优化问题的局部最优解，该算法是屏障法的一种，屏障法可以将复杂的约束问题转化为一系列简单的非约束问题。内点算法相较活动约束系列方法在处理具有大量设计变量和不等式约束的优化问题时有很大的优势，可以求解具有上万个设计变量的大规模非线性优化问题，不仅能用于结构拓扑优化，还可用于常规的结构尺寸优化和形状优化。

NASTRAN的结构优化过程如图1所示。

图1 NASTRAN的结构优化过程

1.2 Nastran的拓扑优化方法

目前最新版的NASTRAN采用变密度方法进行拓扑优化，变密度法也称人工材料法，是受均匀化方法的启发发展而来的，是结构拓扑优化的一种较为有效的物理描述方法［9］。变密度法采用一种密度在0～1之间连续可变的人工材料，将规格化的材料特性与材料的相对密度按一定比例相关，即用幂次关系定义材料特性与密度之间的比例：

式中：ρ0和E0是材料的完整密度和弹性模量；p是惩罚系数，其取值应大于1以使设计变量x的结果逼近0或1，通常取2≤p≤4。

完成拓扑优化问题的物理描述之后，NASTRAN同样利用近似概念［2］将其转化为求解一系列显式的近似问题，并采用MSCADS优化器的序列无约束极小化方法或IPOPT优化器的线性搜索过滤内点算法进行优化搜索。

NASTRAN的拓扑优化方法特别适于解决基于总体设计响应如结构刚度、振动模态及位移的优化问题，对基于局部设计响应如单元应力和应变的优化问题则不太适合。拓扑优化通常会面临棋盘效应、拓扑结果难以制造、网格较密时易产生许多微结构或因变量太多产生巨大的计算成本等一系列问题。NASTRAN成功地解决了这些难题，它通过预设过滤操作克服了棋盘效应，通过最小结构尺寸限制极大地控制了子结构的数量，另外还通过定义各类工艺约束确保拓扑结果便于制造。

2 小水线面双体船的结构优化

横向载荷作用通常是主导小水线面双体船结构设计的最重要载荷工况，因此本文只在横向对开力作用下对主要横向强框结构进行拓扑优化、形状及尺寸优化。横向对开力及边界条件按《CCS小水线面双体船指南》（2005）的要求确定并施加。

2.1 原始的结构有限元模型

小水线面双体船舱段的结构分析模型及常规的横向强框结构形式如图2、图3所示。

图2 舱段结构分析模型

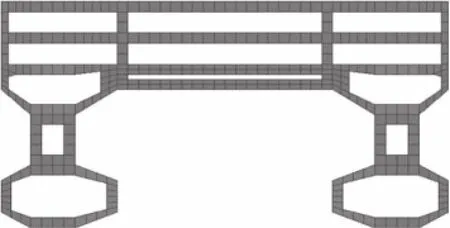
图3 常规的横向强框形式

2.2 强框结构的拓扑优化

从总体布置和实用角度考虑，位于上层舱室内的横向强力结构不太可能采用非常规的形式，因而拓扑优化的设计空间只定义在第3层甲板以下区域，见图4。拓扑优化以整体结构在横向对开力作用下的柔度最小为目标，以拓扑优化结果与原始结构的质量比例为约束。本文分别以0.3、0.4、0.5以及0.6倍的质量保留比例作为约束，分横向对开力向内、向外或同时考虑向内向外两种作用3个工况，共进行了12次拓扑优化设计。

图4 拓扑优化的区域

综合分析各次拓扑优化的结果，承受横向载荷的主要结构，即舷台与支柱体区的横向强框的拓扑形式比较一致，获得了收敛较好的拓扑优化结果，可选0.5倍质量保留比例时的拓扑结果作为典型形式，见图5。

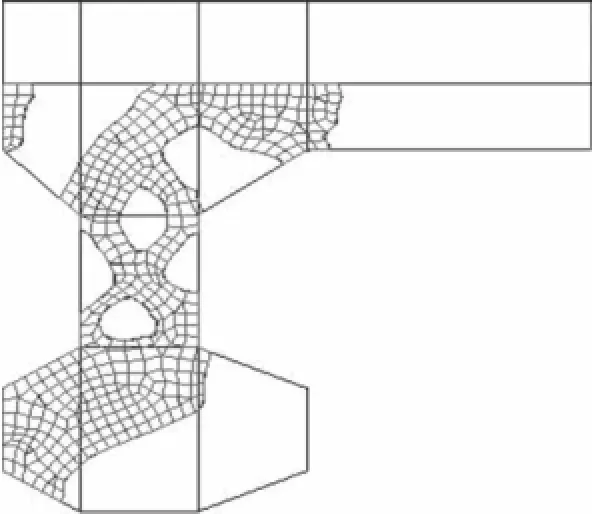
图5 拓扑优化的结果

下潜体内强框的拓扑结果差别较大。原因可能是由于下潜体强框的材料分布对横向力作用下船体的整体刚度影响不大，即该设计区域内目标响应的灵敏度较低，因而仍采用常规的结构形式。综合考虑拓扑优化结果和实际结构的其他设计要求确定的最终优化形式见图6。

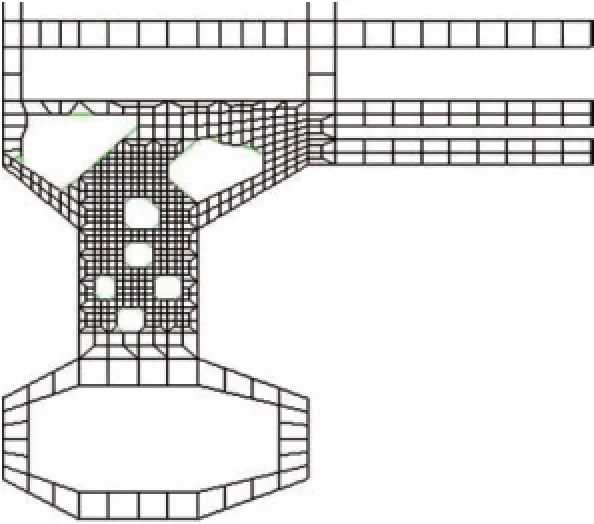
图6 最终的优化结果

为验证拓扑优化获得的强框形式的承载效率，计算对比了图3所示的常规形式与图6所示的优化形式在同样对开力作用下的响应见图7 -图10。向载荷的传递路径上。

图7 常规形式的位移

图8 常规形式的冯氏应力

图9 优化形式的位移

图10 优化形式的冯氏应力

2.3 强框结构的形状优化和尺寸优化

对于上层甲板间的常规强框结构可以通过形状优化和尺寸优化进一步合理确定其腹板高度和厚度的分布规律。

表1列出了构成形状和尺寸优化设计模型的设计变量、设计特性、基本形状变化向量、设计约束以及设计目标。

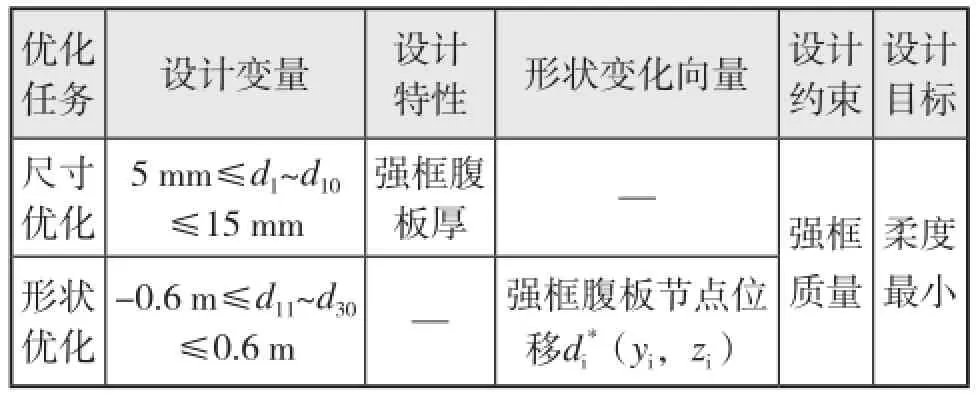
表1 常规强框结构的形状优化和尺寸优化

NASTRAN可以在一个优化任务中同时进行形状优化和尺寸优化，最终通过12次优化循环得到收敛的优化结果，如图11 -图13所示。

图11 设计目标的优化过程

由图7 -图10可见与常规形式相比，优化形式的位移降低21.7%，冯氏应力降低17.1 %，说明基于柔度最小化的拓扑优化，能同时减小结构的应力响应。另外优化后强框上的应力分布比较均匀，应力值较大，也说明优化后的强框有效地承担了主要的横向载荷，该强框形式的材料合理地布置到横

图12 设计变量的优化过程

通过形状优化和尺寸优化，在拓扑优化结果的基础上将舱段结构的横向刚度提高8.2%。

图13显示了优化后上层甲板区域强框腹板厚度的分布及腹板高度的变化。由图可见：在片体宽度范围内的强框应当加强，其腹板的优化厚度已达设计厚度的上限，腹板的高度也相应增加了；而连接桥中间的强横梁可以适当减弱，其腹板的优化厚度也达到设计厚度的下限。

为了继续验证以柔度最小化为目标的结构优化对于减小应力响应的贡献，以形状优化和尺寸优化后的强框腹板高度和厚度更新拓扑优化后的模型，在相同横向对开力下计算其结构响应结果，见图14、图15。比较图14、图15与图9、图10的结果，发现通过形状优化和尺寸优化使结构的位移减小了7.9%，应力降低17.4%，这些结果说明强框腹板厚度和高度优化分布极大提高了其承载效率。如果进而比较图14、图15与图7、图8的结果可知，在同样的横向对开力作用下，连续通过拓扑优化和形状、尺寸组合优化得到的优化结构相比原来的常规结构，变形减小28%，冯氏应力减小31.5%，而增加的质量只占整个舱段质量的2.65%，通过上述三类优化设计明显提高结构的承载效率。

图13 优化后腹板高度及厚度

图14 优化后结构的总变形

图15 优化后结构的冯氏应力

3 结 论

本文简单介绍NASTRAN的一般优化设计方法和拓扑优化方法，并利用这些方法对小水线面双体船的主要横向强框结构进行优化，对优化结果还进行计算验证。优化和验证结果显示NASTRAN的拓扑优化、形状优化和尺寸优化功能是非常有效的。此外，以柔度最小化为目标进行优化设计能极大提高优化的效率，且其优化结果往往能同时大幅降低结构的应力响应。

［1］ MSC. Design Sensitivity and Optimization. 2010.

［2］ Habibi A. New approximation method for structural optimization ［J］. Journal of Computing in Civil Engineering，2012（2）： 236-247.

［3］ Hansen L，Horst P. Multilevel optimization in aircraft structural design evaluation ［J］. Computers and Structures， 2008，86 ：104-118.

［4］ 夏利娟，金咸定. MSC/NASTRAN的结构优化设计方法与应用［C］. MSC用户论文集，2001.

［5］ Stavroulaki M，Stavroulakis G，Leftheris B. Modelling prestress restoration of buildings by general purpose structural analysis and optimization software the optimization module of MSC/NASTRAN ［J］. Computers and Structures，1997（1）： 81-92.

［6］ Holzleitner L，Mahmoud K. Structural shape optimization using MSC/NASTRAN and sequential quadratic programming ［J］. Computers and Structures， 1999，70： 487-514.

［7］ 龙腾，刘莉，彭磊.基于可行方向序列无约束极小化技术外点法的改进协同优化策略［J］. 机械工程学报，2013（3）：52-60.

［8］ Wachter A， Biegler L. On the implementation of a primaldual interior point filter line search algorithm for large-scale nonlinear programming ［J］. Mathematical Programming，2006（1） ：25-57.

［9］ 左孔天，陈立平，钟毅芳，等.基于人工材料密度的新型拓扑优化理论和算法研究［J］.机械工程学报，2004（12）： 31-37.

Structural optimization of SWATH base on MSC/NASTRAN

WEI Gang
(College of Naval Architecture, Ocean and civil Engineering, Shanghai Jiaotong University, Shanghai 200030,China)

This paper introduces the structural optimization algorithms and the implementation procedure of the MSC/NASTRAN， including the mathematical model of the general structural optimization and the physical model of the topology optimization. The cabin of a small waterplane area twin hull （SWATH） is optimized by the topology， shape and size optimization aiming at the improvement of the overall stiff ness of the cabin structure. Then it proposes a reasonable optimized design close to the optimization results considering the engineering applicability. The improvement of the structure response of the optimized design scheme is validated by comparison with the regular design through the direct fi nite element calculation.

SWATH； structure optimization； topology optimization； transverse strength

U674.951

A

1001-9855（2015）06-0035-05

2015-05-07

魏 刚（1983-），男，硕士在读，工程师，研究方向：船舶结构研究设计。