自升式钻井平台倾斜试验及参数敏感性研究
2015-11-17孙承猛朱亚洲林海花赵云鹤
孙承猛朱亚洲林海花赵云鹤
(1.渤海装备辽河重工有限公司 盘锦 124010;2. 哈尔滨工程大学 船舶工程学院 哈尔滨 150001)
自升式钻井平台倾斜试验及参数敏感性研究
孙承猛1朱亚洲2林海花1赵云鹤1
(1.渤海装备辽河重工有限公司 盘锦 124010;2. 哈尔滨工程大学 船舶工程学院 哈尔滨 150001)
自升式钻井平台倾斜试验是确定平台建造完工后实船空船质量、重心的常规试验方法。文章介绍了自升式钻井平台倾斜试验的基本原理和方法,并针对常规的悬臂梁移动产生倾覆力矩的倾斜试验方法,以某座自升式钻井平台倾斜试验数据为例,分析了试验过程中有关试验数据读取误差对试验结果的影响。通过对试验相关参数的敏感性分析,得出参数间的敏感性,为试验设计人员及现场数据读取人员提供有意义的借鉴和参考。
自升式钻井平台;倾斜试验;悬臂梁;敏感性
引 言
近年来,随着海洋油气资源的开发增长,国内外海洋工程装备制造业如火如荼[1]。自升式钻井平台作为近浅海石油钻探的重要装备[2-3],各大船厂、企业纷纷进入自升式平台的设计建造领域。倾斜试验是平台建造完成后为确定其空船质量和重心位置所进行的一项重要试验。目前,对船舶倾斜试验技术所进行的研究较多[4-6],已经比较成熟,并形成了船舶标准[7],而对海洋平台的倾斜试验方法和标准研究仍然较少。例如,有学者进行了半潜平台倾斜试验数据误差研究[8];有学者针对自升式钻井平台倾斜试验,结合工程实际,给出了利用悬臂梁移动进行倾斜试验的方法和过程[9];也有学者采用软件模拟试验过程,提前分析试验阶段各相关参数选取的合理性,以避免盲目试验带来的结果偏差[10]。本文主要介绍自升式钻井平台倾斜试验的基本原理和方法,并分析了该方法中相关试验参数对试验结果的敏感性影响,以期对设计和试验人员有所警醒和帮助。
1 试验基本原理
自升式钻井平台倾斜试验的目的是通过试验方法确定平台空船质量及重心的实际位置。
1.1 空船质量
通过静水力方法能够方便而快捷地得到平台的空船质量。具体方法为:在平台满足试验的条件下,即满足试验大纲要求的初始纵横倾角度、风力等级、海流条件等[7],测量平台首尾部在左右舷舷边的四点吃水(常规船舶考虑到中拱或中垂,通常测量首中尾六点吃水),经换算得到平台的平均吃水;然后通过查静水力曲线,可得此时平台的排水量;最后计及平台试验时的多余质量和不足质量,即可得到平台的空船质量。
1.2 空船重心
按照船舶静力学[11]的基本原理,平台在小角度倾斜时,其倾斜力矩与倾斜角度的正弦值之间呈线性关系,如式(1)所示:

式中:θ为横倾角;?为船舶排水量;GM为初稳性高,表示平台重心与稳心的距离,即:

式中:KM为横稳心高度;KG为重心高度。
假设移动重物或改变压载水状态,此时将产生一个倾斜力矩Mh,即:


由此可知,在小角度倾斜时,平台稳心高度KM和排水量?仅与平台吃水和线型有关。因此,若移动一定质量的重物或压载水产生倾斜力矩,并测得对应的船舶倾斜角度,则可依照式(4)得到平台的重心高度ZG。
另外,平台静止漂浮条件下将满足浮态平衡方程,如式(5)所示:
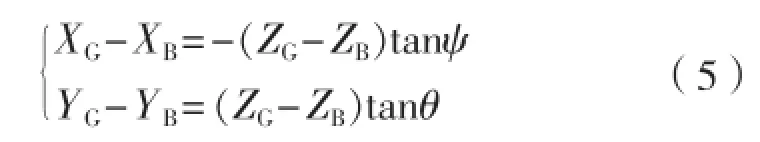
式中:笛卡尔坐标系下,(XG,YG,ZG)为重心坐标; (XB,YB,ZB)为浮心坐标(可查静水力曲线或利用测量吃水软件计算得到);θ为横倾角,ψ为纵倾角,二者可由测量吃水计算求得。
从而,平台重心的纵向坐标XG和横向坐标 YG可由式(6)求得:
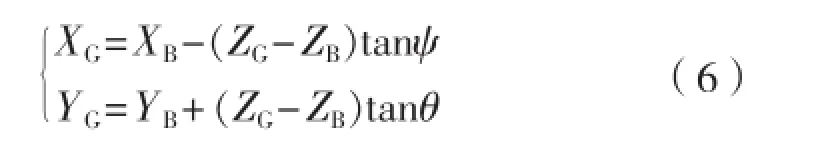
2 试验方法
式中:W为移动重物或改变压载水的质量,l为移动的等效距离。
由式(1)、式 (2)、式 (3)可得:
2.1 倾斜力矩
传统的船舶倾斜试验是采用沿船宽方向移动铁块或压载水等,使其产生横倾,通过测定横倾角,并结合前述方法得到其质量与重心位置的。然而,自升式钻井平台甲板设备布置密集,空间狭小[10],难以采用移动重物方式进行倾斜试验;其常见的三角形外形及压载舱室布局特点使移动压载水方法也较难满足试验精度要求,对自升式钻井平台必须采用不同的试验方法。自升式钻井平台一般采用悬臂梁纵向移动方式产生倾斜力矩,该方式具有以下三个优点:
(1)可以较为精确测定悬臂梁移动时的质量。这是由于平台对钻井载荷控制严格[12],需通过称重试验确定悬臂梁及钻台质量。
(2)悬臂梁具有便捷可靠的移动装置,为试验可行提供保证。
(3)平台外形通常左右对称,悬臂梁的纵向移动不会使平台产生较大的横倾。
2.2 倾角测量
通常可采用两种方法测量平台倾角。
一种方法是挂摆法,如图1所示。设挂摆线的长度为λ,摆动幅度为a,则倾角θ可按式(7)求得:


图1 挂摆法倾角测量示意图
需注意的是,挂摆线长度应有足够的长度(至少为3 m);挂摆应没入水槽或油槽中,且在最大倾角时挂摆不触及槽壁。
另一种方法是U型玻璃管法,如图2所示。假设玻璃管至水箱中心距离为λ,玻璃管读数变化值为a,则倾角θ同样可按式(7)求得。

图2 U型玻璃管法倾角测量示意图
需注意的是,玻璃管与水箱间距离应足够大,且读数范围满足最大倾角要求;水箱液面面积与玻璃管面积比应不小于1 000∶1。
3 参数敏感性分析
假设倾斜试验时悬臂梁及钻台的质量为Wb,悬臂梁单次移动距离为s,采用U型玻璃管侧倾角装置(挂摆法类似),玻璃管单次读数变化为x,试验时平台吃水为d,排水量为?和稳心高度KM均为d的函数,则可由式(4)可求得平台重心高度,如式(8)所示:
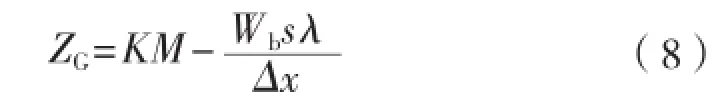
为便于直观反映式(8)中的各参数对重心高度的影响敏感性,本文以某型自升式钻井平台倾斜试验数据作为参考。
该平台倾斜试验时各参数为:d = 4.32 m,?= 9 890 t,KM=51.48 m,Wb=1 250 t,s=1.5 m,x=0.085 m,λ=16.0 m。
以下分别给出倾斜力矩参数、倾角测量参数和平台吃水参数的敏感性分析结果。
3.1 倾斜力矩参数
3.1.1 悬臂梁质量
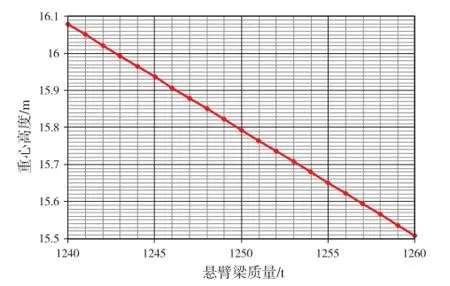
图3 悬臂梁质量敏感性曲线
图3为悬臂梁质量敏感性曲线。可见,随着悬臂梁及钻台质量Wb的增大,平台重心高度不断减小,且下降速度均匀。在试验数值1 250 t附近,Wb每增加1 t,将使重心高度下降约0.029 m,偏差百分比约为0.18%。
3.1.2 悬臂梁单次移动距离
图4为悬臂梁单次移动距离敏感性曲线。可见,随着悬臂梁单次移动距离s的增大,平台重心高度不断减小,且下降速度均匀。在试验数值1.5 m附近,s每增加1 cm,将使重心高度下降0.238 m左右,偏差百分比约为1.5%。

图4 悬臂梁单次移动距离敏感性曲线
3.2 倾角测量参数
3.2.1 玻璃管读数变化值
图5为玻璃管读数变化值敏感性曲线。可见,随着玻璃管读数变化值x的增大,平台重心高度不断增大,但增加速度呈下降趋势。在试验数值0.085 m附近,x每增加1 mm,将使平台重心高度增加约0.415 m,偏差百分比约为2.6%。
3.2.2 玻璃管与水箱中心距离
图6为玻璃管与水箱中心距离敏感性曲线。可见,随着玻璃管与水箱中心距离λ的增大,平台重心高度不断减小,且下降速度均匀。在试验数值16.0 m附近,λ每增加1 cm,将使重心高度下降0.022 m左右,偏差百分比约为0.14%。

图6 玻璃管与水箱中心距离敏感性曲线
3.3 平台吃水参数
图7为平台吃水敏感性曲线。可见,随着平台吃水d的增大,平台重心高度不断减小,且下降速度先较小后增大然后又减小。在试验数值4.32 m附近,d每增加1 cm将使重心高度下降0.024 m左右,偏差百分比约为0.15%。
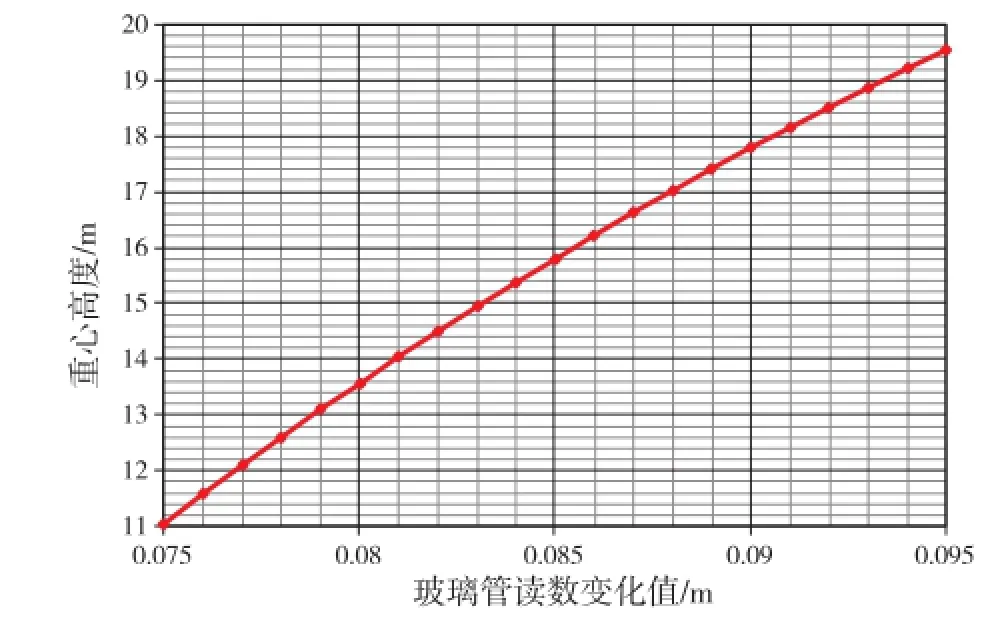
图5 玻璃管读数变化值敏感性曲线

图7 平台吃水敏感性曲线
上述对重心高度的敏感性分析都是基于倾斜试验过程中各参数可能存在的测量误差考虑的。重心高度偏差对比情况如下页表1所示。

表1 参数敏感性分析对比
考虑到倾斜试验过程中各有关参数的测量方法及精度,结合图3 -图7以及表1对比分析,可以看出:
(1)悬臂梁单次移动距离s和玻璃管读数变化值x对重心高度敏感性最高, 较小的读取误差可能造成重心高度的较大差异。
(2)悬臂梁质量和玻璃管与水箱中心距离λ对重心高度敏感性较低,些许的测量误差一般不会引起重心高度的较大变化。
(3)平台吃水d与重心高度的敏感性与平台型线有关,但敏感性较低,其测量误差一般不会引起重心高度的较大变动。
4 结 论
通过上述介绍与分析可以知道,自升式钻井平台的倾斜试验方法与常规船舶基本类似,仅受限于其布局及外形特点,大多采用悬臂梁纵向移动方式产生倾斜力矩。通过分析平台倾斜试验过程中相关参数对重心高度的敏感性,使我们了解了各参数读取偏差对重心高度结果的影响程度。对于敏感性较高的参数,试验人员需要采取多次测量、提高测量精度以及数据后处理等方法,使其对试验结果的影响降至最小[13-14]。
[ 1 ] 苗玉坤,赵学峰. 我国海洋石油装备现状及市场前景[J]. 石油矿场机械, 2011(9):29-32.
[ 2 ] 陈红,李春祥. 自升式钻井平台的发展综述[J]. 中国海洋平台,2007(6):1-6.
[ 3 ] 张用德,袁学强. 我国海洋钻井平台发展现状及趋势[J]. 石油矿场机械, 2008(9):14-17.
[ 4 ] 吴凤辉. 舰船倾斜试验的力矩产生探讨[J]. 舰船科学技术, 2015(3):36-38.
[ 5 ] 宋峰,林慰. 船舶倾斜试验中吃水读数的影响因素[J]. 广东造船, 2014(3):45- 47.
[ 6 ] 许晓玲. 提高船舶倾斜准确性和可靠性的一种方法[J]. 江苏船舶, 2010(1):43-44.
[ 7 ] 杨存国,虞玮. CB/T 3035-2005,船舶倾斜试验[S].北京:国防科学技术工业委员会,2005.
[ 8 ] 陈书敏,肖元,张健效,等. 半潜平台倾斜试验数据误差分析[J]. 船海工程,2015(2):161-163.
[ 9 ] 刘新宝,程龙,曹士峰,等. 悬臂梁式钻井平台倾斜试验方法探索[J]. 中国造船,2011(z1):148-152. [10] 顾恩凯,黄维平,孙铭远. 自升式钻井平台倾斜试验方法研究[J]. 中国造船, 2011(z1):138-144.
[11] 盛振邦,刘应中. 船舶原理[M]. 上海:上海交通大学出版社,2003.
[12] 孙承猛,吕宏伟,戴克文,等. 自升式钻井平台悬臂梁载荷图谱编制方法研究[J]. 石油矿场机械,2013 (11):20-23.
[13] 林金,罗素琴. 倾斜试验中初稳性高度最小二乘法计算方法解析与应用[J]. 造船技术,2011(1):7-10.
[14] 班业平. 浅谈大型船舶倾斜试验的控制要点[J]. 船舶,2014(2):22-25.
On inclining test of jack-up and parameter sensitivity analysis
SUN Cheng-meng1ZHU Ya-zhou2LIN Hai-hua1ZHAO Yun-he1
(1. China Petroleum Liaohe Equipment Company, Panjin 124010, China; 2. College of shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
The inclining test of a jack-up aims at the regular testing of the center of gravity of the built light weight ships. This paper introduces the basic theory and method of the inclining test of the jack-up. The inclining test of the inclining moment produced by a moving cantilever is performed based on the data of a jack-up to analyze the infl uence of the recording error of the relevant experimental data on the experimental results. It analyzes the sensitivity of the parameters in the experiments to obtain the highly sensitive factors, which can provide signifi cant reference for experiment designers and fi eldwork recorders.
jack-up; inclining test; cantilever; sensitivity
TE951
A
1001-9855(2015)06-0024-05
2015-06-28;
2015-07-15
孙承猛(1979-),男,博士,高级工程师,研究方向:船舶与海洋结构物总体设计。
朱亚洲(1982-),男,博士在读,工程师,研究方向:船舶与海洋工程结构物总体设计及结构安全评估。
林海花(1979-),女,博士,高级工程师,研究方向:船舶与海洋工程结构物计算分析。
赵云鹤(1984-),男,工程师,研究方向:船舶与海洋工程结构物总体设计。
