基于非线性输出频率响应函数的多裂纹转子故障诊断方法研究

李志农，杜宜光，肖尧先

（南昌航空大学航空制造工程学院，江西南昌330063）

基于非线性输出频率响应函数的多裂纹转子故障诊断方法研究

李志农，杜宜光，肖尧先

（南昌航空大学航空制造工程学院，江西南昌330063）

相对单条转子裂纹的故障诊断，多条裂纹的故障诊断更复杂，也更困难。以两条裂纹为例，将非线性输出频率响应函数（NOFRF）引入到具有两条裂纹转子系统的故障诊断中，提出了一种基于NOFRF的多裂纹转子故障诊断新方法，并且对比分析了两条裂纹不同夹角、不同裂纹深度下NOFRF值的变化情况。实验结果表明，NOFRF值对裂纹故障具有很高的敏感性，根据NOFRF值的变化情况，不仅能反映转子系统裂纹是否存在，还能反映两条裂纹之间的夹角、裂纹深度的变化情况。因此，利用NOFRF值，可以有效地监测转子系统中多条裂纹故障。

动力机械工程；非线性输出频率响应函数；裂纹转子；故障诊断；裂纹夹角；裂纹深度

0 引言

在与转子有关的各种故障中，裂纹故障具有难于发现、诊断困难，后果严重的故障特征。20世纪70年代据加利福尼亚电力研究所统计［1］，透平发电机组发生的23起故障中，有8起是低压转子轴和发电机轴横向裂纹引起，占故障总数的35%.同时，国内时常也有转子裂纹事件的报道，姚孟电厂在维修时发现了一部电机的主轴上有3条裂纹，其中最深的一条裂纹深度竟达到直径的2/3.涡喷六发动机在使用的过程中，也曾多次发生涡轮轴近盘根部处产生裂纹以至折断的严重事故。因而，能否及时发现裂纹故障，对防止发生灾难性转子断裂事故，减少非计划停机及提高经济效益具有重大意义。目前，针对具有单条裂纹故障诊断的研究取得了很大进展［1-6］。相比单裂纹故障，产生多裂纹故障的转子系统非线性特性更强，危险性更大，后果也将更为严重。因此，对于转子系统上多裂纹故障的诊断也越来越被重视。印度学者Darpe等［7］采用集中质量法建立转子模型，研究了含双呼吸型裂纹转子的动力学特性。于涛等［8］从断裂力学理论出发，讨论了双裂纹转子系统非线性动力学特性，为多裂纹转子系统故障识别提供了理论依据。文献［9］采用较为简单的余弦型裂纹呼吸模型，利用有限元方法，分析了含两条裂纹的转子系统动力学特性。Chasalevris［10］建立了转子裂纹的柔度矩阵，利用小波分析的方法，研究了弯矩作用下梁上双直裂纹的检测方法。

以上裂纹故障的检测方法根据对系统输入输出信号处理方式的不同，可以分为两大类:一类是利用传感器获得的信号来分析，另一类是考虑系统模型来诊断。二者的区别在于前者只考虑了系统的输出信号，而后者不仅考虑了系统的输出信号，而且还考虑了系统的激励。很显然，前者只对输入稳定的系统才有效。后者克服了前者存在的不足，因为输出信号的变化有可能是系统的激励引起，而系统的固有特性并没有改变，这时仅根据输出信号的变化来诊断势必会造成误判。

故此，基于非线性模型的故障诊断方法得到很快发展。其中，英国Shiefld大学Lang等［11-14］从Volterra级数出发，提出了非线性输出频率响应函数（NOFRF）的概念，并推导出NOFRF的辨识方法。该方法不仅能清晰准确地反映出系统输出频谱与非线性参数之间的关系，而且各阶次的函数都是一维的，从而可方便地用图表分析来解释。Peng等［15-18］在NOFRF理论也做了一些有意义的探索，并将NOFRF的概念应用于振动信号分析和结构的裂纹故障检测中。李志农博士领导的课题组利用NOFRF方法对转子裂纹故障进行了有效地辨识，得出了转子上含有横向裂纹、斜裂纹的NOFRF特

性［19-20］。

然而，现有的基于NOFRF的转子裂纹故障诊断方法主要是针对转轴上具有单条裂纹展开的，对于采用NOFRF对转子上具有多条裂纹的转子系统特性研究少有涉及。基于此，本文引入NOFRF理论并对转子系统上含有两条横向裂纹展开辨识，提出了基于NOFRF的两条裂纹转子系统的故障诊断方法。通过实验研究，分析了不同裂纹夹角、不同裂纹深度时转子系统各阶NOFRF值的变化特征，为具有多条裂纹的转子系统故障诊断提供了一种新的有效方法。

1 非线性输出频率响应函数理论及其辨识算法

NOFRF是在Volterra级数模型的基础上提出来的，可用于研究一大类的非线性系统的动态特征。假设u（t）和y（t）分别为非线性系统的输入和输出，则该系统的Volterra级数模型可以表示为

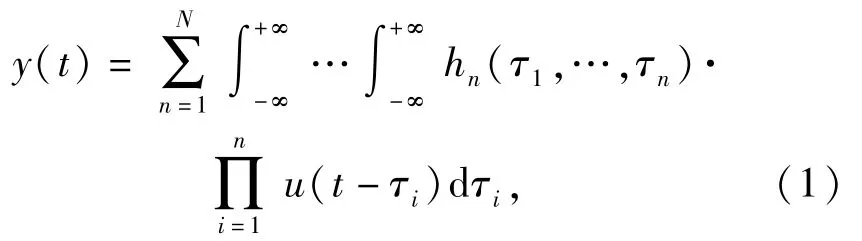
式中:hn（τ1，…，τn）为非线性系统的第n阶Volterra核，n=1，2，……，N；t为时间；τ为时延。相应地，非线性系统的输出在频域内的表达式为

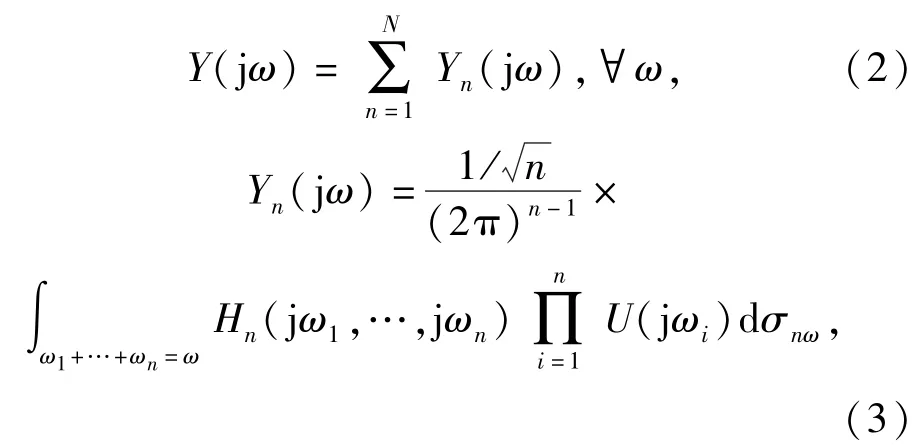
式中:Yn（jω）表示第n阶非线性系统的输出频率响应；Y（jω）是该系统输出y（t）的傅里叶变换；U（jω）是该系统输入u（t）的傅里叶变换；Hn（jω1，…，jωn）表示非线性系统的第n阶广义频率响应函数。

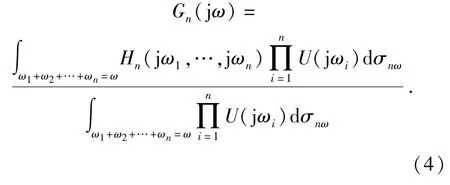
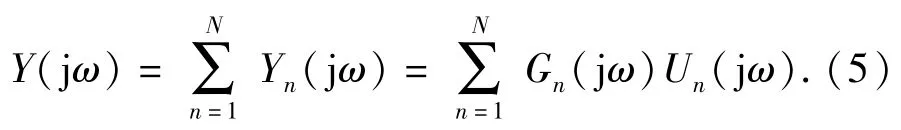
对照传统的线性系统输出频率响应函数，如图1所示，发现（5）式所描述的NOFRF表达形式和线性系统的输出频率响应函数相似，NOFRF是线性系统输出频率响应函数Y（jω）=G1（jω）U（jω）的自然延拓。类似地，（5）式所描述的非线性系统输入输出频谱关系可以用图2来描述。

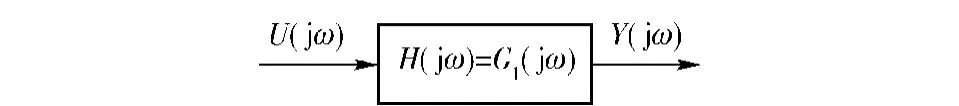
图1 线性输入输出频率响应关系Fig.1 The frequency response between output and input of a linear system

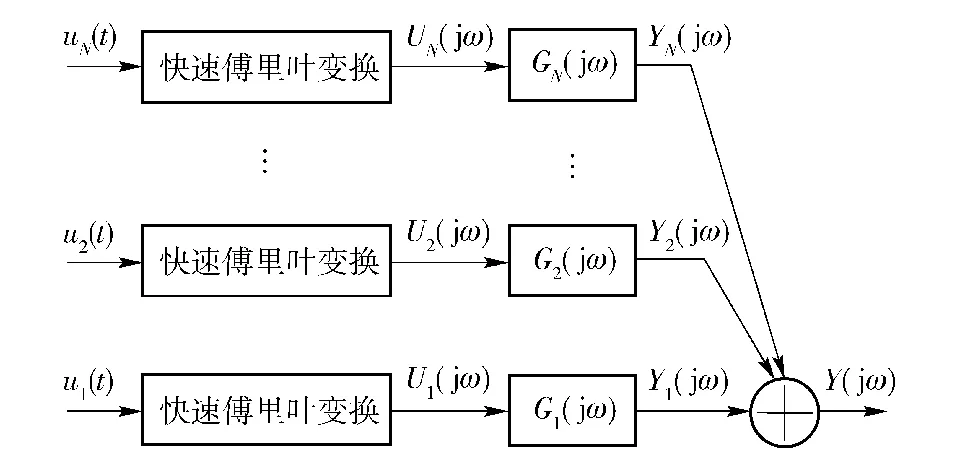
图2 非线性系统输入输出频率响应关系Fig.2 The frequency response between output and input of a nonlinear system

NOFRF可用于反映系统的振动特性，与广义频率响应函数（GERF）相比，其各阶核值也可由采集的输入输出信号确定，但是，NOFRF有一个更加重要的特征，即其各阶次的函数都是一维的，可以较容易地根据系统的输入、输出信号估计得到，避免产生维数灾难。

由（5）式可知，非线性系统的输入输出函数关系可改写成

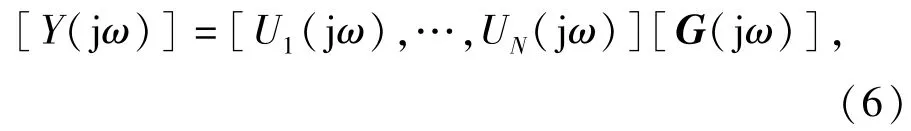
式中:G（jω）=［G1（jω），…，GN（jω）］T.令u（t）= αu*（t），α为一个不为0的常数，u*（t）为非线性系统的输入信号，则

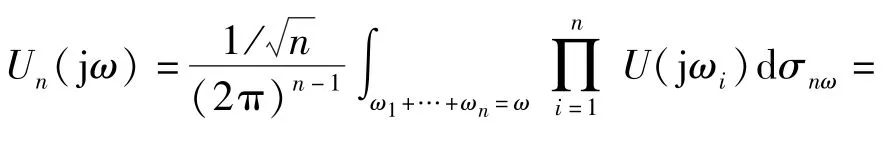
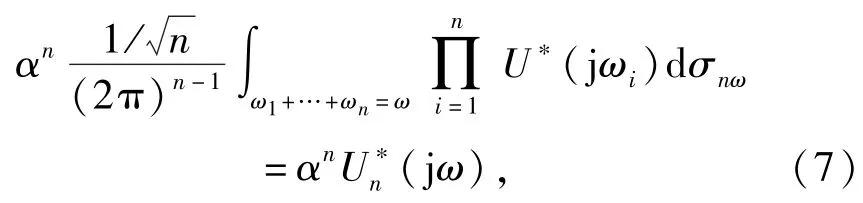
式中:U*（jω）是u*（t）的傅里叶变换，且

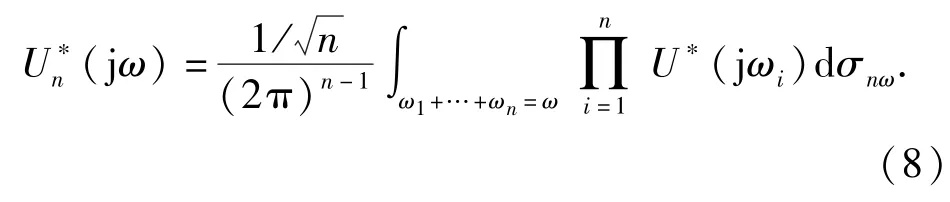
因此，（7）式还可进一步改写为

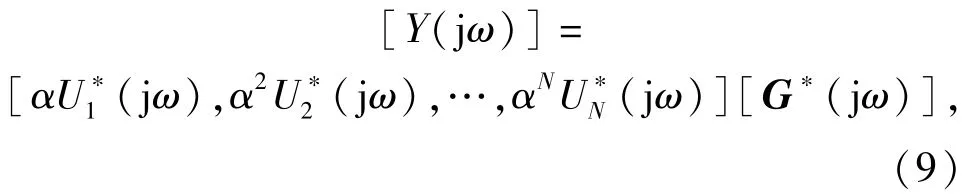
在转子动力学测试中，一般采用谐波输入。所谓谐波输入是指输入信号为正余弦输入信号。当系统在受到谐波信号输入时，即

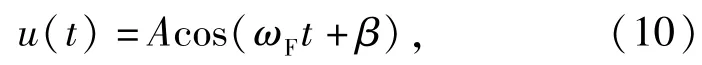
式中:ωF为谐波输入信号频率。根据文献［18］，（2）式还可以改写为

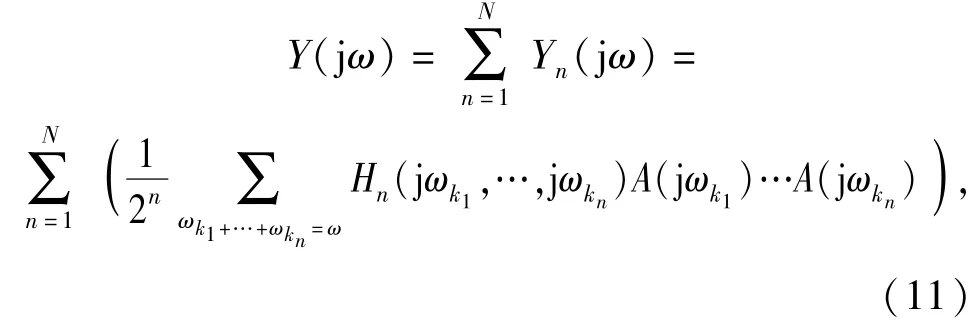
式中:

为了方便起见，定义系统的n阶输出频率分量为Ωn，则根据（11）式系统的输出频率分量可以表示为

式中:Ωn由频率集合｛ω｝确定，即

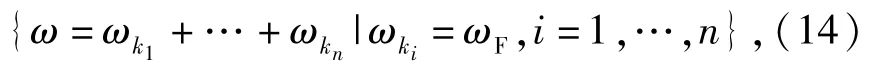
式中:当所有的ωk1，…，ωkn均为-ωF时，则ω= -nωF；当其中有k个为ωF时，ω=（-n+2k）ωF.因此输出Yn（jω）的频率成分为

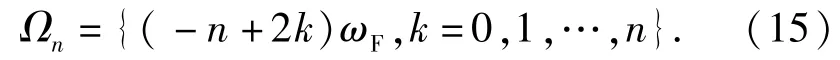
则（13）式进一步改写为

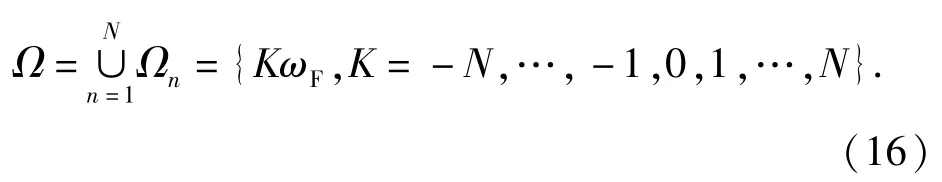
（16）式很好地解释了非线性系统仅有谐波激励时可以激发出多次谐波的原因。

因此，非线性系统的输出频谱Y（jω）为

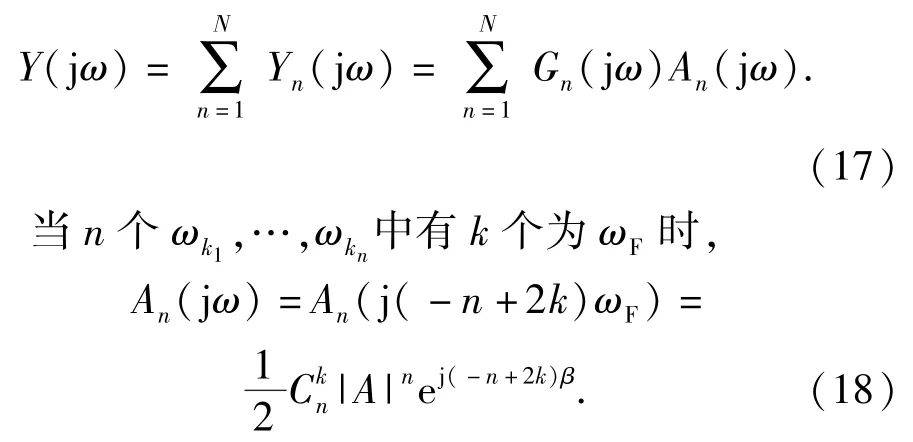
在采用NOFRF分析转子系统的故障特性时，由于4倍频以上的频率成分幅值很小，可以忽略不计，而且阶数越高，系统辨识的计算量也越大。通常只考虑到前4阶频率输出即可。因此，由（17）式，并考虑（18）式，可以得到如下4个式子:

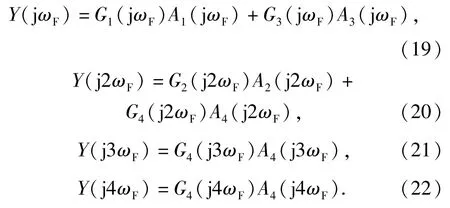
分析（19）式～（22）式可以发现，采用两个频率相同但幅值不同的谐波激励信号去激励系统，便可以求出系统各阶NOFRF值。例如，采用两个幅值分别为U（1）、U（2）的正弦波信号激励系统，对应系统的输入频谱为A（1）q（jωF）、A（2）q（jωF），q=1，2，3，4.相应的输出频谱为Y（1）（jωF）和Y（2）（jωF）.根据（19）式得

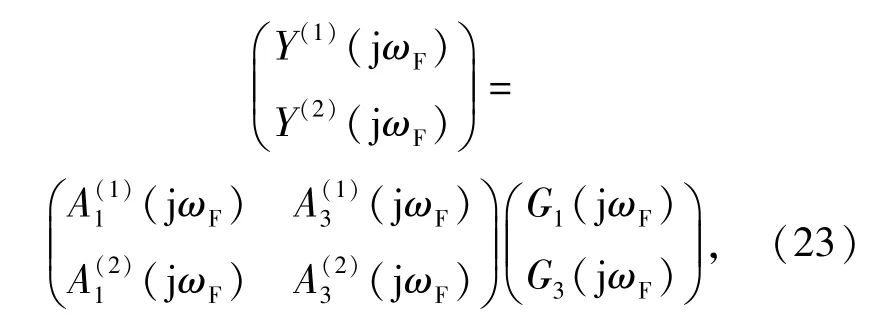
即

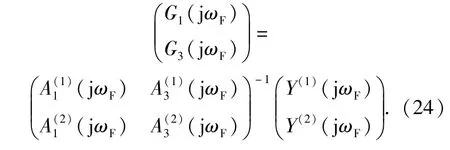
同理，转子系统其他各阶NOFRF值均可通过（19）式～（22）式的变换求得。

2 实验研究

图3所示为转子实验台示意图，转子上两裂纹分别为横向裂纹且紧邻中间转盘左右两侧，通过安装在支承座上的电涡流传感器采集裂纹转子的振动位移信号。取10根相同属性的转轴用于实验研究，其中1根转轴不作处理用于比较，另外9根转轴采用线切割技术加工得到不同的裂纹轴。根据加工裂纹的深度把这些裂纹轴分成3组。第1组两裂纹相对深度比均为a/R=0.2，两条横向裂纹在其转轴左端面上投影的裂纹夹角γ分别为0°、45°、90°.第2组左侧裂纹相对深度比为a1/R=1.0，右侧裂纹相对深度比为a2/R=0.2，投影面上的裂纹夹角γ分别为0°、45°、90°.第3组裂纹相对深度比均为a/R=1.0，裂纹夹角γ分别为0°、45°、90°.所有裂纹轴都具有相同的几何尺寸和材料属性，即裂纹轴的长度L=260 mm，裂纹轴直径为d=9.5 mm，弹性模量E=210 GPa，泊松比ν=0.3，阻尼系数c= 41.65 kg/s，转盘尺寸φ76 mm×25 mm，转盘质量m=0.595 kg，转盘的不平衡偏心距e=0.16 mm，无裂纹时转子系统横向振动固有频率为98.8 Hz.由于转子上裂纹的存在，其固有频率会发生变化，但变化相对较小，且裂纹转子在1/2固有频率处的振动特性比较明显，所以在实验研究中设定裂纹转子转速n=3 000 r/min.对该非线性转子系统横向方向上的输入输出进行同步采样，采样时每周采样64个点，采样8个周期。

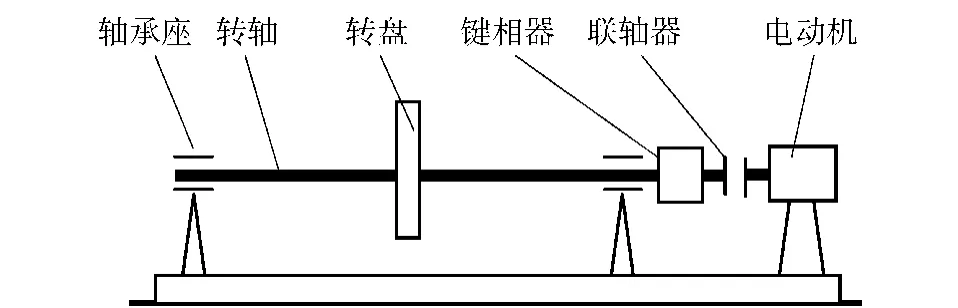
图3 转子实验台示意Fig.3 Schematic diagram of rotor test bench

首先，从转子系统输出频谱上对该非线性系统进行分析。图4所示为该实验台采集得到的无裂纹转子系统输出频谱图。从图中可知，无裂纹转子正常工作下的输出频谱是典型的基频振动，其他频率成分非常微弱，可以忽略不计。

图5所示为当两条裂纹均为浅裂纹，即两裂纹相对深度比a1/R=a2/R=0.2时，裂纹转子系统输出频谱图。从图中可以清晰地发现，两条裂纹在不同裂纹夹角下系统的输出频谱会呈现有规律的变化，即随着两条裂纹夹角逐渐增大，1倍频幅值无明显变化，2倍频变化明显且其幅值随着裂纹夹角的增加而减小；当两条裂纹夹角γ为0°和45°时，会有微弱的3倍频出现，当两条裂纹夹角γ=90°时，反复实验均可发现此时系统输出频谱中2倍频、3倍频分量幅值不再突出，单独就该裂纹夹角下的频谱图而言，得到的输出频谱特性和无裂纹轴的输出频谱特性非常类似，这时，仅从频谱图中无法准确地推断转子系统上是否有裂纹存在。

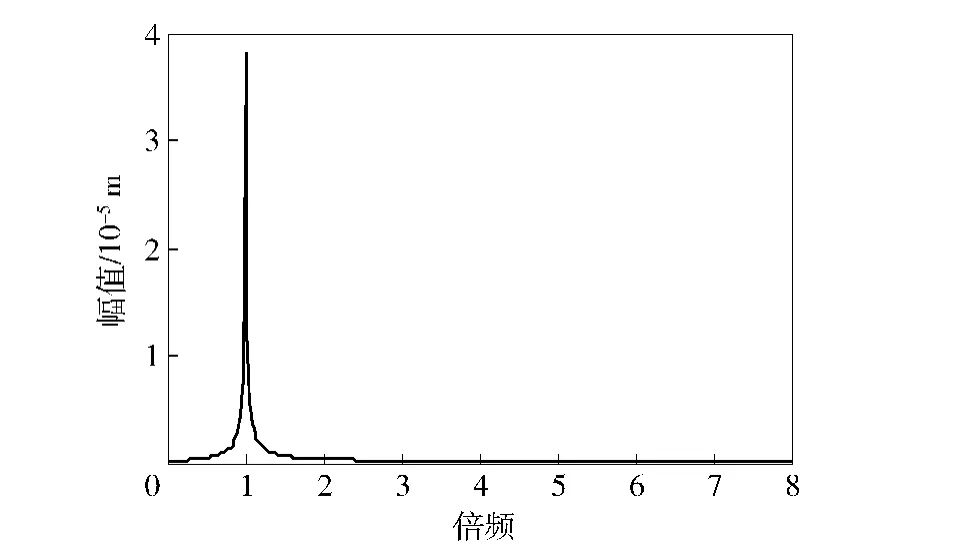
图4 无裂纹轴系统输出频谱Fig.4 The output spectrum（normal rotor）

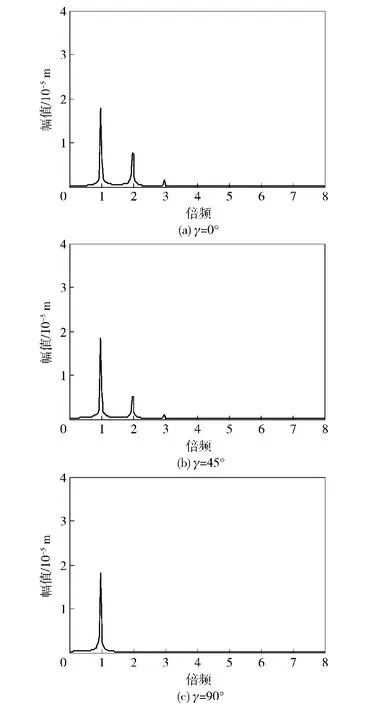
图5 a1/R=a2/R=0.2时系统输出频谱Fig.5 The output spectrum for a1/R=a2/R=0.2

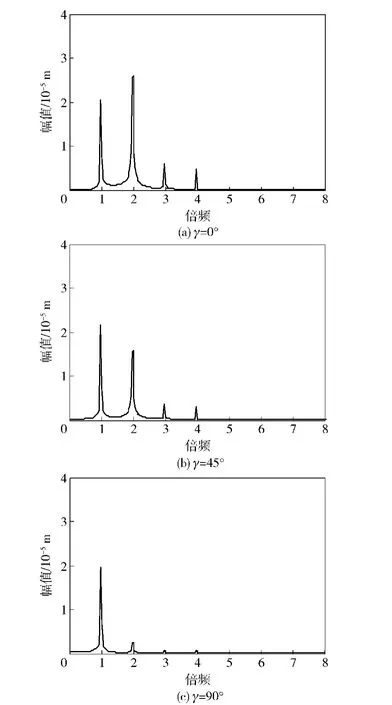
图6 a1/R=1.0和a2/R=0.2时系统输出频谱Fig.6 The output spectrum for a1/R=1.0 and a2/R=0.2

图6所示为左侧裂纹相对深度比a1/R=1.0，右侧裂纹相对深度比a2/R=0.2下，具有两条裂纹的转子系统输出频谱图。比较图5和图6可以发现，增加左侧裂纹深度使其由浅裂纹变为深裂纹后，系统输出频谱中1倍频、2倍频仍旧明显，同时伴有3倍频，4倍频等多倍频分量的出现，且当两裂纹夹角较小时多倍频分量非常明显。因此，增加转子系统上裂纹深度，系统输出频谱中各倍频分量幅值增加并伴有更多倍频成分出现，系统表现出更强的非线性特性。观察图6中不同裂纹夹角下系统输出频谱图，可以发现与图5具有相似的变化规律，即随着两条裂纹夹角逐渐增大，基频幅值变化微弱，2倍频、3倍频、4倍频等多倍频分量幅值会随着两裂纹夹角的增大而不断减小，且2倍频分量幅值变化最为显著。当γ=90°时，多倍频分量虽然存在但并不明显。

图7所示为两裂纹相对深度比都为1.0，即a1/R=a2/R=1.0下，具有两条裂纹的转子系统的输出频谱图。该图再次验证了图6得到的结论，即当两裂纹较深时，系统输出频谱中1倍频、2倍频仍旧明显，同时会伴有3倍频、4倍频等多倍频的出现，系统输出频谱中各倍频分量幅值也会增加，系统表现出更强的非线性特性。不同的是，当两裂纹深度均较深时，输出频谱中3倍频非常明显且其幅值远大于较为明显的4倍频分量幅值。同时，随着两条裂纹夹角逐渐增大，2倍频、3倍频、4倍频等多倍频分量幅值仍旧随着两裂纹夹角的增大而不断减小，在该变化过程中，2倍频分量幅值变化最为显著。

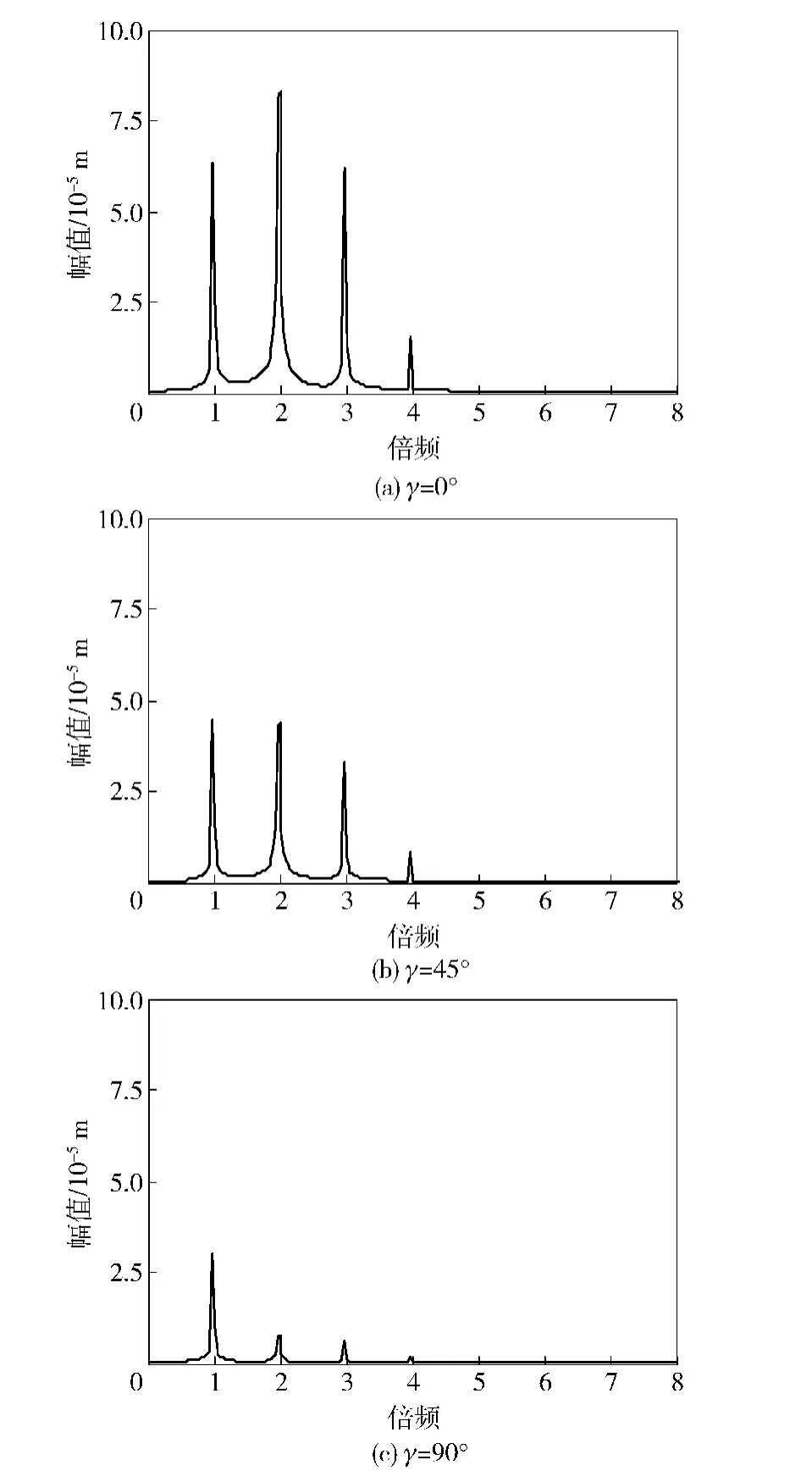
图7 a1/R=a2/R=1.0时系统输出频Fig.7 The output spectrum for a1/R=a2/R=1.0

整体来看，该转子系统输出频谱中2倍频、3倍频、4倍频等多倍频分量幅值的变化可有效反应转子系统上两裂纹夹角的变化情况，且2倍频分量幅值的变化最为显著。同时，随着裂纹深度的增加，系统输出频谱图上会有更多的倍频分量出现且较为明显，系统表现出更强的非线性特性。

然后，再从各阶非线性输出频率响应函数特性上对该非线性系统进行分析，利用（19）式～（22）式得到的不同裂纹深度、不同裂纹夹角的裂纹轴的各阶NOFRF值如表1～表3所示，表中所有的数据都进行了处理，即用得到的各阶NOFRF值均除以G1（jωF）得到不大于1的数。对于无裂纹转轴，经过理论推导，其应该只有G1（jωF）值不为0，其他各阶NOFRF值均为0.而通过该方法的辨识，得到的输出频率响应函数中其他各阶NOFRF值结果并不为0，这主要是由随机信号的干扰和计算误差所致。然而，与相比较，其他各阶NOFRF值都非常小，几乎可以忽略不计。因此，对于无裂纹转轴，值可以完全反映了系统的本质传递特性。

表1 a/R=0.2时不同裂纹夹角下辨识系统的NOFRF值Tab.1 NOFRF values（a/R=0.2）

表2 a1/R=1.0和a2/R=0.2时不同裂纹夹角下辨识系统的NOFRF值Tab.2 NOFRF values（a1/R=1.0，a2/R=0.2）

表3 a/R=1.0时不同裂纹夹角下辨识系统的NOFRF值Tab.3 NOFRF values（a/R=1.0）

对于表1中，当两裂纹均为浅裂纹，裂纹夹角γ=90°时，与无裂纹轴相比较，除以外的其他NOFRF值均远大于无裂纹轴的NOFRF值，这些NOFRF值的大小反映了监测系统的非线性特性，而在转子上存在浅裂纹时的频谱图中是反映不出来的，显示了该方法的独特优势。因此，该方法有效地解决了当转子上存在浅裂纹时，采用研究该系统输出频谱特性的方法对裂纹夹角γ=90°时的裂纹故障无法检测的问题。

3 结论

相对单条转子裂纹的故障诊断，多条裂纹的故障诊断更复杂，也更困难。基于NOFRF的独特特性，即该理论不仅能清晰准确地反映出系统输出频谱与非线性参数之间的关系，而且各阶次的函数都是一维的。基于此，本文将非线性输出频率响应函数理论引入到具有两条裂纹的转子系统的故障诊断中，利用该方法对比分析了两条裂纹不同夹角、不同的裂纹深度下的各阶NOFRF值的变化，并得到了一些非常有价值的结论，具有重要的理论价值和工程应用价值。

1）当转子系统上有浅裂纹存在时，若采用传统的频谱图分析方法对转子裂纹故障的存在无法辨识时，可以利用NOFRF对裂纹故障的敏感性有效地克服其不足，实现转子裂纹故障的有效检测。2）在无裂纹的转子系统正常运行状态下，值可以完全反映系统的本质传递特性，其他各阶核值与G1（jωF）相比较，几乎可以忽略不计，一旦裂纹出现，各阶NOFRF值急剧增大。3）NOFRF值不仅能反映转子系统裂纹的存在，而且能反映两条裂纹之间的夹角、裂纹深度的变化情况。NOFRF值中的变化情况对两条裂纹的夹角非常敏感，尤其G2（j2ωF）随着两裂纹夹角的增大而大幅减小；NOFRF值中的变化情况可用于判定裂纹转子系统中两条裂纹深度的变化情况，即随着裂纹深度的增加，逐渐变大。

（

）

［1］Armor A F.On-line monitoring of turbine-generator shaft cracking，83-JPGC-Pwr-7［R］.US:ASME，1983.

［2］向家伟，陈雪峰，何正嘉，等.基于小波有限元和遗传优化算法的转轴裂纹诊断［J］.机械强度，2008，30（5）:702-706. XIANG Jia-wei，CHEN Xue-feng，HE Zheng-jia，et al.Crack diagnosis for the shaft based on wavelet finite element method and genetic algorithm［J］.Journal of Mechanical Strength，2008，30（5）:702-706.（in Chinese）

［3］Yu Z G，Chu F L.Identification of crack in functionally graded material beams using the p-version of finite element method［J］. Journal of Sound and Vibration，2009，325（1/2）:69-84.

［4］谢平，杜义浩.基于信息熵的裂纹转子动力特征分析与诊断方法［J］.机械工程学报，2009，45（1）:195-199. XIE Ping，DU Yi-hao.Crack rotor dynamic feature analysis and diagnosis method based on information entropy［J］.Journal of Mechanical Engineering，2009，45（1）:195-199.（in Chinese）

［5］陈雪峰，向家伟，董洪波，等.基于区间B样条小波有限元的转子裂纹定量识别［J］.机械工程学报，2007，43（3）:123-127. CHEN Xue-feng，XIANG Jia-wei，DONG Hong-bo.et al.Quanti-tative identification of rotor cracks based on finite element of B-spline wavelet on the interval［J］.Journal of Mechanical Engineering，2007，43（3）:123-127.（in Chinese）

［6］Li X J，Wang K，Jiang L P，et al.The application of a signal in early cracked rotor fault diagnosis with pwvd and svm［J］.Journal of Software，2011，6（10）:1969-1976.

［7］Darpe A K，Gupta K，Chawla A.Dynamics o f a twocrack rotor［J］. Journal of Sound and Vibration，2003，259（3）:649-675.

［8］于涛，孙伟，韩清凯.双裂纹转子系统非线性动力学特性研究［J］.振动与冲击，2013，32（19）:144-152. YU Tao，SUN Wei，HAN Qing-kai.Nonlinear dynamic behavior of a dual-crack rotor system［J］.Journal of Sound and Vibration，2013，32（19）:144-152.（in Chinese）

［9］温诗铸，郭丹.具有两条裂纹的转子系统的振动研究［J］.机械强度，2005，27（2）:135-139. WEN Shi-zhu，GUO Dan.Vibration analysis of a rotor with two cracks［J］.Journal of Mechanical Strength，2005，27（2）:135-139.（in Chinese）

［10］Chasalevris A C.Identification of multiple cracks in beams under bending［J］.Mechanical System and Signal Processing，2006，20（7）:1631-1673.

［11］Lang Z Q，Billings S A，Yue R，et al.Output frequency response function of nonlinear volterra systems［J］.Automatica，2007，43（5）:805-816.

［12］Lang Z Q，Billings S A.Energy transfer properties of nonlinear systems in the frequency domain［J］.Journal of Sound and Vibration，2005，78（5），354-362.

［13］Lang Z Q，Peng Z K.A novel approach for nonlinearity detection in vibrating systems［J］.Journal of Sound and Vibration，2008，314（3/4/5）:603-615.

［14］Lang Z Q，Billings S A，Tomlinson G R，et al.Analytical description of the effects of system nonlinearities on output frequency responses:a case study［J］.Journal of Sound and Vibration，2006，295（3/4/5）:584-601.

［15］Peng Z K，Lang Z Q.The nonlinear output frequency response functions of one-dimensional chain type structures［J］.Journal of Applied Mechanics，2010，77（1）:11-27.

［16］Peng Z K，Lang Z Q，Billings S A，et al.Analysis of locally nonlinear MDOF systems using nonlinear output frequency response functions［J］.Journal of Vibration and Acoustics，2009，131（5）:51-63.

［17］Peng Z K，Lang Z Q，Billings S A，et al.Crack detection using nonlinear output frequency response functions［J］.Journal of Sound and Vibration，2007，301（3/4/5）:777-788.

［18］Peng Z K，Lang Z Q，Billings S A，etc.Analysis of bilinear oscillators under harmonic loading using nonlinear output frequency response functions［J］.International Journal of Mechanical Sciences，2007，49（11）:1213-1225.

［19］员险锋，李志农，林言丽，等.基于非线性输出频率响应函数的裂纹故障诊断方法研究［J］.机械强度，2013，35（2）: 133-137. YUAN Xian-feng，LI Zhi-nong，LIN Yan-li，et al.Rotor crack fault diagnosis method based on nonlinear output frequency response function［J］.Journal of Mechanical Strength，2013，35（2）:133-137.（in Chinese）

［20］员险锋.基于非线性输出频率响应函数的转子裂纹故障诊断方法研究［D］.郑州:郑州大学，2011. YUAN Xian-feng.Crack rotor fault diagnosis method based on nonlinear output frequency response function［D］.Zhengzhou: Zhengzhou University，2011.（in Chinese）

Fault Diagnosis Method of Rotor System with Multi-crack Based on Nonlinear Output Frequency Response Function

LI Zhi-nong，DU Yi-guang，XIAO Yao-xian
（School of Aeronautical Manufacturing Engineering，Nanchang Hangkong University，Nanchang 330063，Jiangxi，China）

The fault diagnosis of rotor system with multi-crack is more complex and more difficult than the fault diagnosis of rotor system with single crack.The nonlinear output frequency response function（NOFRF）is introduced to fault diagnosis of rotor system with two cracks，and a fault diagnosis method of rotor system with two cracks based on the NOFRF is proposed.The NOFRF values of two cracks with different crack angles and crack depths are compared.The experimental results show that the NOFRF values are very sensitive to different crack angles and different crack depths，and the existence of rotor crack fault and the variation of crack angle and crack depth can be reflected by the NOFRF values.Therefore，the sensitivity of the NOFRF values to the crack fault can be effectively used for the detection of a rotor system with multi-cracks.

power machinery engineering；nonlinear output frequency response function；cracked rotor；fault diagnosis；crack angle；crack depth

O347.6；TH165.3

A

1000-1093（2015）06-1096-08

10.3969/j.issn.1000-1093.2015.06.019

2014-09-09

国家自然科学基金项目（51265039、51075372、50775208）

李志农（1966—），男，教授。E-mail:lizhinong@tsinghua.org.cn