侵彻过载曲线特征参量数值模拟研究

靳 鸿 ，唐 波 ， 靳书云 ，陈昌鑫 ， 王 欢

（1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051；3.北京航天自动控制研究所，北京 100854）

0 引 言

弹体在侵彻靶体过程中，由于受到靶体阻力作用所具有的负加速度，通常称为弹体的侵彻过载[1-2]，它反映了加速度随时间的变化规律。从20世纪60年代开始，各个国家的军工研究者对侵彻过载测试进行了大量研究[3]。17世纪50年代，Euler和Robbins就对弹体侵彻各种靶体进行过试验研究，在总结试验条件和数据的基础上提出了相应的侵彻经验公式[4]。20世纪80年代以来，国内许多学者也对侵彻过载测试进行了研究[5-6]。但由于目标介质的多样性和实验条件的复杂性，侵彻原型试验需要耗费大量的人力、物力，还不能确定试验的有效性，因此数值模拟成为研究侵彻试验的主要方法之一，如LS-DYNA，AU-todyn，Dytran 等[7]。

在钻地弹药系统研发、侵彻效果评估、弹体侵彻硬目标时的高g值等过程中，侵彻过载是一个重要的被测值[8]。弹丸的加速度-时间曲线体现了弹丸侵彻过程中的运动状态，对于精确的延时引信研制、高质量高性能的侵彻武器研制、侵彻的物理模型建立等非常重要[9]。本文利用LS-DYNA对不同条件下弹体侵彻靶板进行仿真分析，对侵彻过载曲线特征参量进行研究。

1 过载基本过程与过载特征参量

1.1 过载曲线及过载基本过程

典型的过载曲线如图1所示，包括脉宽、峰值等。当弹丸头部刚与靶板接触时，弹丸头部与靶板表面相交处的横截面较小，侵彻阻力不大，因而减加速度也不大；随着侵彻深度的增加，弹丸头部与靶板表面相交处的横截面不断增大，当该横截面的直径与弹径相等时，侵彻阻力接近最大值；当侵彻深度继续增加时，侵彻阻力的增加是由弹丸外表面与靶体的接触面积增大而使摩擦力增大，加速度接近于最大加速度；随着侵彻深度的增加，克服侵彻阻力消耗的能量也越大，从而使弹丸的运动速度逐渐降低，当弹丸速度变化为零时，侵彻阻力也为零，减加速度也随之消失变为零[10]。

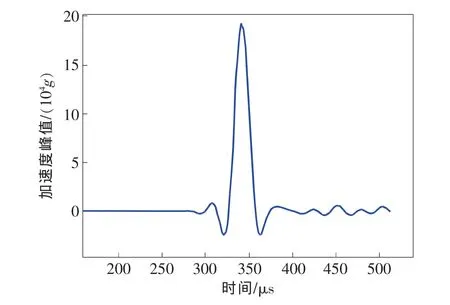
图1 典型的过载曲线

1.2 过载特征参量

根据对过载曲线的分析，若以侵彻加速度达到最大值时弹丸侵入的长度作为此时的侵彻路程，侵彻速度是加速度的一次积分，侵彻行程是加速度的二次积分。大量试验表明：弹体撞击速度越高，弹体的侵彻深度越深。

钱伟长[11]在《穿甲力学》中指出主要影响侵彻过程的5个关键参量：1）弹丸着靶速度和着角；2）弹体的形状和尺寸；3）靶体的厚度；4）弹体的材料性能（抗拉强度、抗剪强度、密度）；5）靶板的材料性能（抗拉强度、抗剪强度、密度）。赵国志等[12]归纳了6类主要影响侵彻过程的关键参量：1）弹丸着靶速度和着角；2）弹头的形状和尺寸；3）弹体的质量和质量分布；4）弹体材料的性能（强度、硬度、冲击性、密度等）；5）靶板厚度；6）靶板材料的性能（ 强度、硬度、冲击性、密度等）。

2 仿真实验

2.1 计算基本假设

数值模拟实验中弹体与混凝土靶板网格单元均采用ANSYS/LS-DYNA内部提供的三维Lagrange算法，该算法使网格单元附着在材料上并随着材料的流动而产生单元的形变。建模采用g-cm-μs单位体系。

建立弹体和靶板结构的几何模型时，对仿真过程中弹体和靶板作以下假设：

1）弹体和靶板均视为均匀连续，弹体视为刚体，视混凝土靶板为无限域，无初始应力，不计边界效应。

2）弹体垂直侵彻混凝土靶板，即侵彻倾角为0，不计重力作用。

3）整个侵彻过程绝热，不计空气阻力，不计弹体振动影响。

2.2 材料模型及参数

在进行数值模拟实验时，材料模型的选择对仿真结果的影响至关重要。文中弹体和钢板靶板均选择常用的非线性塑性模型PLASTIC_KINEMATIC[13]。

弹体材料选用45#钢，参数如表1所示。

表1 钢的材料参数

混凝土靶板采用Johnson-Holmquist-Concrete损伤积累模型，并添加MAT_ADD_EROSION材料模型，设定抗拉强度，添加拉伸失效准则，才能使混凝土靶产生由于微裂纹扩展贯通形成的成坑崩落现象，从而能获得与实际相符的结果。参数如表2所示。

表2 混凝土的材料参数

3 靶厚度对侵彻特征参量影响

固定弹丸初速度和侵彻介质，改变靶的厚度进行ANSYS仿真，得到曲线如图2所示。图中曲线B、A、C、D、E 分别对应靶厚度为 0.6，1.0，1.4，1.8，2.2cm。

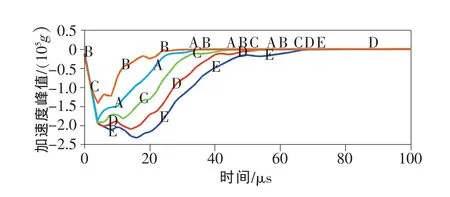
图2 不同厚度靶的侵彻加速度仿真波形

由图得出，靶厚度影响加速度曲线的脉宽、峰值和上升时间等特征参量。图中各曲线0~2μs时间内斜率相同，2μs后峰值、时间斜率开始降低，并且厚度越厚，斜率越平缓、上升时间越长、峰值越高、脉宽越宽。将图2中0~4μs时间内波形进行放大，如图3所示。

图3 图2局部放大波形图

由于弹丸初速相同，所以各条曲线在0~2μs时间内斜率相同。表3为图1所对应各特征参量值。

表3 图1所对应各特征参量值

2μs后弹丸撞击靶板，由于靶厚度不同，每个弹丸所受阻力也不相同。因此，加速度有所变化，速度有所变化。

4 弹丸初速度对侵彻特征参量影响

厚度、介质相同，初速度不同时，加速度仿真曲线波形如图4所示。图中A、B、C、D、E曲线分别对应初速度为：500，700，900，1100，1300m/s。初速度越大，曲线斜率越大、上升时间越短、峰值越高、脉宽越窄。表4为图4所对应各特征参数量。

5 峰值与脉宽特征参量变化分析

加速度波形的峰值、脉宽与多种因素有关，但是不同因素对峰值、脉宽的影响程度不同。弹丸初速和靶板厚度对侵彻加速度曲线都有影响，图5、图6给出了上面两组仿真条件下，加速度峰值、脉宽的变化情况。由图5可以看出，靶板厚度的变化对峰值的影响较小，但初速变化使峰值有较大的变化量。在图6中，初速对脉宽影响较大。

表4 图4所对应各特征参量值

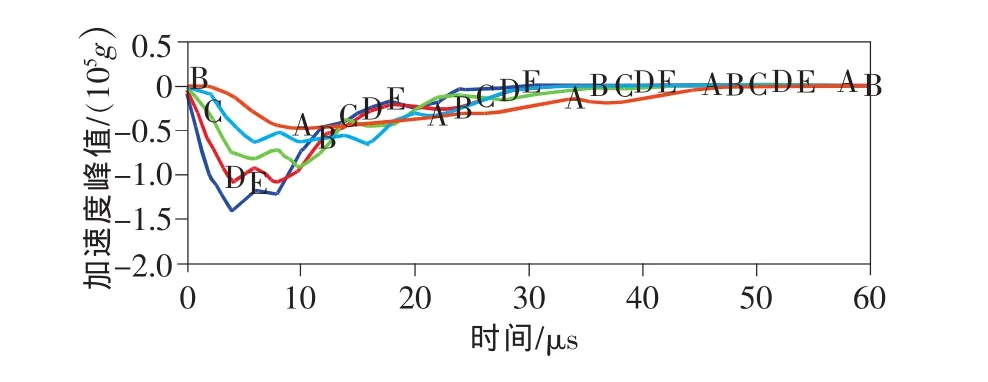
图4 初速度不同的侵彻加速度仿真波形

图5 峰值变化与加速度、厚度关系

图6 脉宽变化与加速度、厚度关系

侵彻介质也对侵彻加速度曲线的特征参量具有显著的影响。介质的类型不同，加速度波形的脉宽、峰值等特征参量也有所不同。对相同初速、厚度，不同介质做6组仿真，任意两种不同的介质加速度表现不同的规律，如图7所示。

6 结束语

本文通过利用ANSYS/LS-DYNA对侵彻过程中弹丸初速、靶板厚度、侵彻介质对侵彻加速度波形的影响进行数值模拟，分析了以上因素与波形峰值、脉宽、上升时间等特征参量的对应关系，为侵彻过程分析提供了一定的参考。

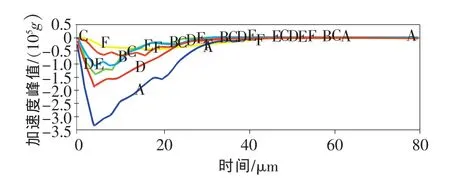
图7 不同介质的加速度曲线

但是，实际侵彻过程多种因素影响。除了数值模拟实验，还要通过试验的方法揭示特征参量与实验条件的关系。

[1]张建仁，刘天生，张晋红，等.弹丸侵彻多层装甲钢板过载特性研究[J].能源与节能，2011（ 3）：81-83.

[2]虞青俊，李玉龙，金连宝，等.侵彻多层混凝土目标弹丸过载特性研究[J].探测与控制学报，2007，29（ 1）：13-17.

[3]刘伟钊，陈侃，李蓉，等.不同介质侵彻过载特征参量有限元仿真方法[J].科学技术与工程，2011，11（ 15）：3494-3497.

[4]徐鹏，祖静，范锦彪，等.高g值加速度冲击试验技术研究[J].振动与冲击，2011，30（ 4）：241-243.

[5]屈新芬，商顺昌，杨晴，等.影响弹丸侵彻性能的因素分析及引信方案探讨[J].信息与电子工程，2003，1（ 3）：51-55.

[6]曹德青.钢筋混凝土侵彻数值模拟研究[D].北京：北京理工大学，2000.

[7]郭香华，张庆明，何远航.混凝土厚靶在弹体正侵彻下的响应研究[J].北京理工大学学报，2011，31（ 7）：765-767.

[8]聂明飞，李玉龙.卵形头部弹侵彻单多层混凝土靶板有限元仿真[J].探测与控制学报，2009，31（ 4）：78-83.

[9]刘璞，施坤林，黄惠东.钢板侵彻过载的三维数值模拟[J].探测与控制学报，2006，28（ 1）：25-28.

[10]孙俊伟，张亚，李世中.弹丸侵彻不同间距靶板的过载特征分析[J].中北大学学报，2013，34（ 1）：24-28.

[11]钱伟长.穿甲力学[M].北京：国防工业出版社，1984：35-41.

[12]赵国志.穿甲工程力学[M].北京：兵器工业出版社，1992：77-80.

[13]He L L， Chen X W.Analyses of the penetration process considering mass loss[J].European Journal of Mechanics A/Soli，2011（ 30）：145-157.