周期应力下非线性退化建模与剩余寿命估计

张少钊，胡昌华，张正新，周志杰，张建勋

（第二炮兵工程大学，陕西 西安 710025）

0 引 言

近年来，预测与健康管理（prognostics and health management，PHM）[1]作为一种新兴技术，在智能电网、核电站、电力工业、航空航天、舰船维护和公共健康管理等领域得到广泛应用，有效地提高了设备的安全性和可靠性，降低了设备的维护保障费用和失效事件发生的风险。预测是PHM的重要组成部分，其中剩余寿命（ remaining useful lifetime，RUL）的预测为优化设备检测与维护策略，合理订购备件提供了科学的依据，因此也是当前可靠性领域研究的重点和热点。

剩余寿命预测的方法主要包括基于物理模型的方法、数据驱动的方法及两种方法的融合[2]。当系统的物理失效模型容易建立时，基于物理失效模型的方法最为准确；但更多的情况下，系统较为复杂，物理失效模型难以建立，其应用也受制于此。基于数据驱动的剩余寿命估计方法由于其适用性更广，得到了广泛的研究和关注。近年来，由于技术的进步和产品开发周期的缩短，设备的可靠性明显提高，失效数据也越来越少，使得基于退化数据的RUL估计方法得到了更多的青睐。其中，基于随机过程的方法由于更能体现退化过程的随机性和动态特征，逐渐成为退化建模的主流[3]，这类方法主要有Wiener过程[4]、Markov 链[5]、Gamma 过程[6]、逆高斯过程[7]等。 Wiener过程是一种特殊的扩散过程，能够对非单调退化过程进行建模[8]，其在首达时间意义下具有解析形式的寿命分布，得到了广泛的应用。选择不同形式的漂移系数，过程可以对线性和非线性退化过程进行建模。Lu和Peng等[9-10]对线性情况下的维纳退化过程做了研究。Si等在文献[11]中提出了一种基于扩散过程的非线性建模方法，将线性退化下的结果包含为一种特例，并在首达时间意义下，导出了剩余寿命的分布函数。

在实际的退化过程中，设备普遍受到周期性变化应力的影响。如设备存贮的环境温度应力在一年中会出现周期性的变化，某些设备的工作载荷也具有周期性。周期应力是汽轮机轴累积损伤的重要因素。然而，目前对这类情况下的退化建模和RUL估计的研究较少。

基于此，本文针对设备的退化过程中应力的作用符合周期性变化的情况，通过在扩散过程的漂移系数中引入周期函数，考虑这种情况下设备的退化建模和RUL估计问题。首先在考虑周期应力作用下，基于扩散过程建立了非线性退化模型，在首达时间的意义下，推导出了剩余寿命的分布，并给出了参数的极大似然估计。通过数值仿真和统计分析验证了剩余寿命分布的正确性和本文所提剩余寿命估计方法的有效性。

1 问题描述

图1是某型电容器耐压强度随使用次数下降的退化曲线，可以看出，电容器的工作电压作为其退化过程中的主要应力，具有明显的周期性特征。

利用退化过程建模是将退化过程描述为一种随机过程{X（ t）；t≥0}，其中 X（ t）是 t时刻的随机退化信号，由确定部分和随机部分所组成。确定部分用来描述系统的固有特征和共性物理特征，而随机部分用来描述系统退化过程中存在的个体差异以及固有的动态性和差异性。

在建立退化模型后，要进行剩余寿命估计，首先需要对设备的寿命进行定义。将设备失效的时间定义为随机退化过程{X（t）；t≥0}首次达到失效阈值l的时间（首达时间），因此，设备寿命T定义为

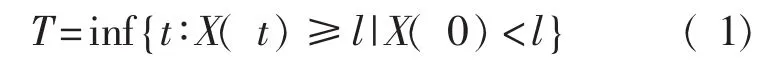
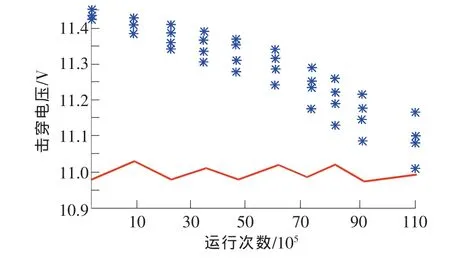
图1 某型电容器样品试验数据示意图

假设 X（ 0）=0，失效阈值 l＞0。 因此，进行剩余寿命估计的关键在于确定首达时间，将设备的退化过程描述为一类扩散过程{X（ t）；t≥0}。

式中t是模型的时间尺度，当退化过程为线性退化过程时，t是采样时间点；B（ t）为标准布朗运动，即 B（ t）～N（ 0，t），N（ 0，t）是均值为 0，方差为 t的正态分布；μ（ t；θ）为漂移系数，与设备所受应力有关；σB为扩散系数，由设备本身存在的不一致性与不稳定性、测量设备测量误差及稳定性、测试过程中的外部干扰等随机因素决定；μ（ t；θ）是时间 t的非线性函数，θ为未知参数。式（2）将退化过程就描述为非时齐的扩散过程。在设备的退化过程中，受到的环境或应力影响可能是不断变化的，μ（t；θ）是随时间的非线性函数，因此可以描述设备所处环境影响随时间不断变化的过程。 并且，当 μ（ t；θ）=μ 时，该模型就是一种线性漂移的扩散过程，这也说明了式（2）更加具有一般性和灵活性。

考虑用式（2）描述周期性应力作用下的退化过程。因为X（t）是随机过程，显然寿命T也是一个随机变量，设寿命T的寿命分布函数为FT（t），概率密度函数（probability density function，PDF）为fT（t）。为了实现寿命估计，关键需要解决以下两个问题：

1）退化模型的参数估计；

2）基于退化模型的剩余寿命估计。

2 周期应力作用下的非线性退化模型与寿命估计

2.1 退化建模

如何对周期性的应力进行描述是退化建模过程中的关键问题。在对具有线性特征的退化数据进行剩余寿命估计时，通常采用线性漂移的扩散过程-Wiener过程的退化模型进行建模。但是，周期应力作用下的退化是一种非线性的过程；并且，在工程实际中非线性的退化过程更具有普遍性，因此考虑将基于Wiener过程的退化模型推广到非线性的情况。

Wiener过程是带漂移的布朗运动。在实际的退化过程中，真实的漂移系数和扩散系数往往不是常数，不能通过直接观测得到；因此，通过扩散过程来描述退化过程中的潜在波动在理论上是可行的。

由于μ（t；θ）表示退化过程中的漂移系数，是一种应力作用的结果。因此，当应力的作用出现周期性特征时，可以将一类满足式（2）的扩散过程X（t）描述为

式中，参数A用来描述退化过程的线性趋势，（B/ω）sin（ωt）用来描述一种周期性的波动，反映了设备受到的环境等周期应力作用下的退化轨迹。

2.2 参数估计

本文采用一种基于历史退化数据的参数估计方法，通过参数极大似然估计对模型的参数进行估计。

假设对n个样品进行性能退化测试，对第i个样品的测量时间为ti1，…，tim，并且在初始时刻ti0时的性能退化量Xi0=0，样品退化量的测量值为Xi1，…，Xim。记ΔXij=Xij-Xi（j-1）为样品i在时刻ti（j-1），tij之间的性能退化量,测量时间间隔Δtij=tij-ti（j-1）。

由Wiener过程的性质可知：

假设各不同退化设备之间的退化量测量值具有独立性，由式（ 4）可以得到未知参数 Θ=[A，B，σB2，ω]′的似然函数

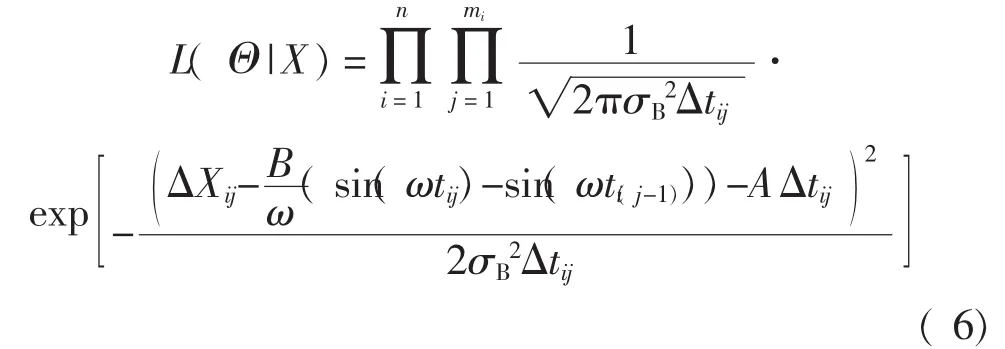
未知参数的对数似然函数可以表示为

因此，Θ的极大似然估计可通过对式（7）取最大化得到。

2.3 剩余寿命估计

确定退化过程的描述形式后，通过推导首达时间概率密度函数，就可以得到剩余寿命的估计值；所以，首达时间概率密度函数在剩余寿命估计的过程中，起到连接退化过程和寿命分布的桥梁作用，推导首达时间概率密度函数是剩余寿命估计的核心问题。

但是在式（ 2）的情况下，当 μ（ t；θ）不是常数时，要通过推导得到首达时间分布的解析式比较困难。如果采用数值仿真的方法，计算量很大，所得结果也不能满足PHM的决策优化要求。为了能够得到首达时间概率密度函数的解析解，Si等在文献[11]中通过以下合理假设，得到了首达时间的渐进解。

假设1：在式（1）下如果设备在t时刻没有失效，那么认为设备在t时刻之前没有发生过失效。

假设 2：潜在的退化过程{X（ t）；t≥0}在 t时刻达到失效阈值，即 X（ t）=l，那么{X（ t）；t≥0}在 t之前穿越失效阈值l的概率可以忽略。

假设1是不考虑设备维修的影响，因为如果设备在运行过程中进行了维修，设备的退化数据就出现了更新，使退化数据从另一个初始状态开始退化，本文考虑的过程是设备在一个退化周期内发生的退化。假设2是为了能够推导出首达时间概率密度函数的解析解。在设备的运行过程中，一般情况下，当退化达到失效阈值时，认为设备继续运行下去存在风险，因此会对设备进行维修检查或者停止使用。然而，在工程实际中，也可能存在设备的退化量在某一时刻达到了失效阈值，又由于某种原因在短时间内回到正常范围的情况；但是，这种事件只是一种小概率的事件，假设2的目的是在计算过程中将这种小概率事件忽略，这在现实中是合理可行的。

基于以上两种假设，可以推导出剩余寿命概率密度函数[12]为

具体的，对于式（3）描述的退化过程，由式（2）可得 μ（ t；θ）=A+Bcos（ ωt）。因此在满足假设 1，2 的情况下，可由式（ 3）推导出{X（ t），t≥0}穿越首达失效阈值l的首达时间概率密度函数为

已知设备的退化过程，假设设备运行到τ时刻仍未失效，且在τ时刻的退化量为xτ（xτ＜l），则设备的剩余寿命Tl可以定义为

基于此，可以推导出剩余寿命密度函数的解析式

2.4 剩余寿命估计算法步骤

基于以上分析，现将周期应力作用下的非线性退化过程剩余寿命估计步骤总结如下：

1）根据退化数据建立式（3）的退化模型；

2）利用退化数据根据式（7）进行模型参数的极大似然估计；

3）确定参数值后利用式（11）进行剩余寿命预测，得出结论。

3 仿真研究

通过数值仿真主要解决两个问题：

1）首达时间概率密度函数的推导是进行寿命预测的一个难点，为了得到式（9），在推导的过程中使用了近似的算法，因此有必要通过数值仿真验证式（9）的正确性和近似准确度。

2）对于数据中失效时间的确定问题，考虑在实际的情况中，退化数据超过阈值的真实时间往往无法获得；因为在实际的数据的采样中，退化超过阈值的时刻不可能刚好在采样点上，而是在两个采样点之间的某个时刻。基于此，本文将数据首次超过失效阈值时所对应的测试时间近似为失效时间。

采用Euler离散化[13]的方法来近似退化过程{X（ t），t＞0}：

其中 Y～N（ 0，1），Δt为离散化步长，θ是未知参数，为了比较首达时间数值解和本文的解析解，在仿真过程中，假设模型的参数已知。

3.1 模型验证

通过数值仿真的方法来近似退化过程{X（ t），t≥0}，通过统计仿真数据中的首达时间数据，绘制首达时间分布直方图，然后通过近似计算得到的解析式（9）绘制的首达时间分布图进行类比。

为了验证模型，首先设定退化过程为

其中初始 X（ 0）=0，设定阈值 l=100，样本轨迹数量M=10000，离散化步长Δt=0.01。为了检验模型的适应性，对退化过程中随机性作用比较大的参数σB分别取3个不同的值：1）令σB取值较小，也就是考虑扩散系数对模型的主导性较小的情况，令σB=2；2）扩散系数适中的情况，令σB=6；3）扩散系数较大的情况，令σB=10。分别绘制这3种情况的首达时间分布直方图和解析结果曲线，如图2所示。

可以看出，数值仿真的首达时间统计结果和解析渐进解的结果基本符合。当仿真的样本数量不断增大，达到一定程度时，仿真数据的首达时间统计结果直方图就会无限趋近于真实的首达时间PDF，基于此，可以验证本文的方法在一定的前提下可以进行首达时间的估计。值得一提的是，当σB=2时，也就是图2（a）的情况下，可以看出，首达时间的PDF近似于逆高斯分布，这也验证了当扩散系数对随机过程的影响比较小时，该模型可以近似于线性模型。

3.2 剩余寿命估计

鉴于Wiener过程在剩余寿命估计中使用较为广泛，将Wiener过程（记为模型M1）同本文提出的模型（记为模型M2）进行比较，这里将失效阈值设为1000。分别采用模型M1和M2对6组仿真数据的退化过程进行建模分析。

根据失效时间的确定方法，平均失效时间（mean time to failure，MTTF）为 226.3h。具体数据如图 3 所示，可以看出，退化数据具有一定的非线性特征。利用上述数据，进行参数估计，通过比较退化模型的平均失效时间和总体均方误差（total mean square error，TMSE）的值来比较模型的拟合效果。具体的结果如表1所示。

表1 Wiener过程模型与本文退化模型的比较

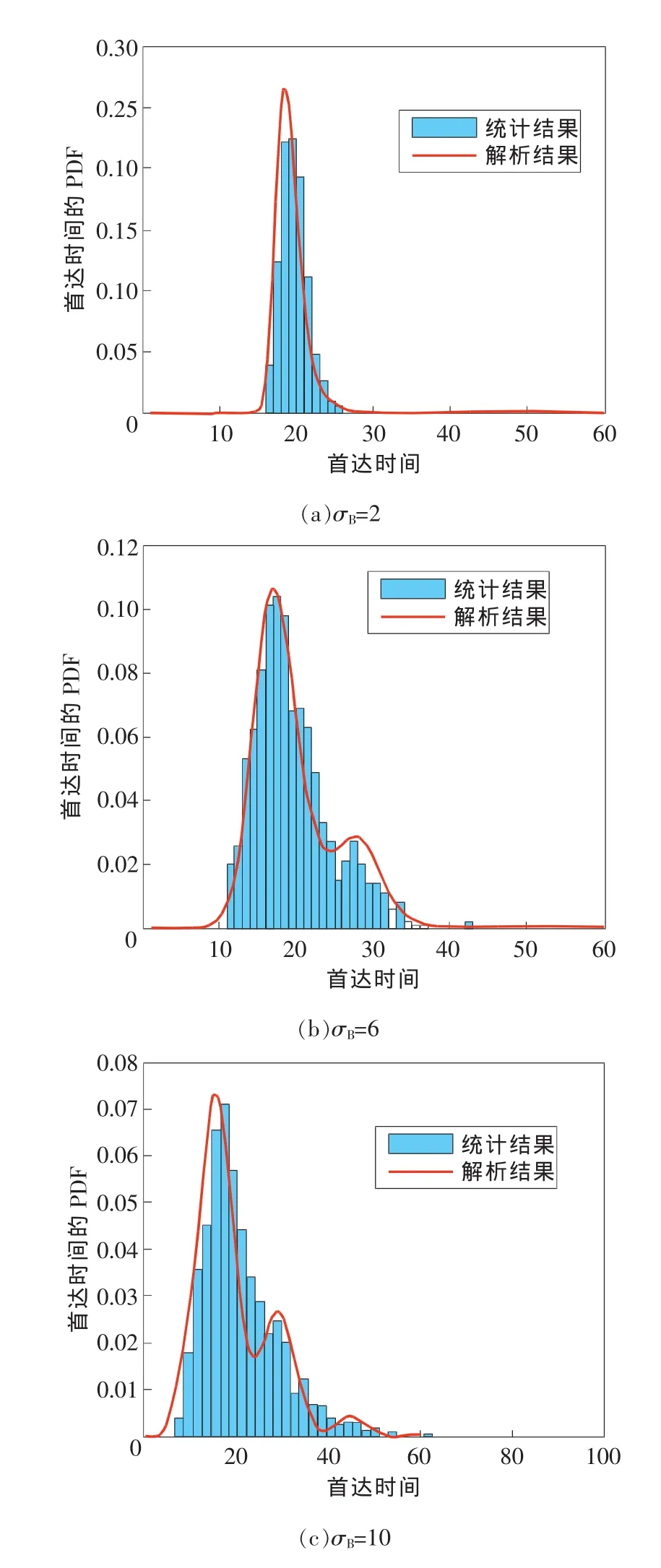
图2 数值仿真首达时间统计和解析渐进解的比较结果

可以看出，本文提出的方法所得到的MTTF值更为接近真实结果，并且本文方法得到的TMSE值也好于线性模型。

图4为不同退化检测点上估计的剩余寿命概率密度函数曲线、实际的剩余寿命曲线和估计的平均剩余寿命曲线。可以看出，本文采用的方法同Wiener过程建模方法得到的估计结果显然有很大的差异，本文方法得到的剩余寿命估计值更接近实际的剩余寿命值。这说明对于受到周期应力作用的非线性退化过程，本文方法所得到的结果更准确。

图3 仿真退化数据

4 结束语

长寿命、高成本、高可靠性设备在贮存或使用过程中可能受到周期性的应力作用，为了描述这种非线性退化过程，本文提出了一种基于扩散过程的退化模型，并在首达时间的意义下通过近似计算推导了相关的剩余寿命分布。通过数值仿真和统计分析验证寿命分布的正确性。可以看出，当退化数据由于周期应力作用而出现非线性波动时，本文提出的模型得到的实验结果优于现有方法，能够为设备的监测维护与管理提供更加准确的决策信息，具有潜在的工程应用价值。

图4 模型M1、M2剩余寿命估计结果比较

本文方法对于周期应力作用的描述更为准确，相比之下得到的估计结果也更加准确，但同时由于寿命分布函数相对复杂，在参数估计时难以得到解析的结果，使得参数估计相比Wiener过程更加复杂，这是下一步亟需解决的问题。

[1]曾声奎，Petch M，吴际.故障预测与健康管理（PHM）技术的现状与发展[J].航空学报，2005，26（ 5）：626-632.

[2]Jardine A K S， Lin D， Banjevic D.A review on machinery diagnostics and prognostics implementing conditionbased maintenance[J].Mechanical Systems and Signal Processing，2006，20（ 7）：1483-1510.

[3]Si X S， Wang W B， Hu C H， et al.Remaining useful life estimation：A review on the statistical data driven approaches[J].European Journal of Operational Research，2011（ 213）：1-14.

[4]Doksum K A，Hoyland A.Models for variable-stress accelerated life testing experimentsbased on wiener processes and the inverse gaussian distribution[J].Theory of Probability and its Applications，1993，37（ 1）：137-139.

[5]Kharoufeh J P.Explicit results for wear processes in A markovian environment[J].Operations Research Letters，2003，31（ 3）：237-244.

[6]Abdel-Hameed M.A gamma wear process[J].IEEE Transactions on Reliability，1975，24（ 2）：152-153.

[7]Wang X，Xu D.An inverse gaussian process model for degradation data[J].Technometrics，2010，52（ 2）：188-197.

[8]Whitmore G A F.Schenkelberg，modelling accelerated degradation data using wienerdiffusion with a time scale transformation[J].Lifetime Data Analysis，1997（ 3）：27-45.

[9]Lu C J，Meeker W Q.Using degradation measures to estimate a time-to-failure distribution[J].Technom-etrics，1993，35（ 2）：161-174.

[10]Peng C Y，Tseng S T.Mis-specification analysis of linear degradation models[J].IEEE Transactions on Relia bility，2009，58（ 3）：444-455.

[11]Si X S， Wang W B， Hu C H， et al.Remaining useful life estimation based on a nonlinear diffusion degradation process[J].IEEE Transactionson Reliability，2012，61（ 1）：50-67.

[12]Kloeden P，Platen E.Numerical solution of stochastic differential equations[M].New York：Springer，1995：71.

[13]Beskos A，Papaspiliopoulos O，Roberts G O，et al.Exact and computationally efficient likelihood-based estimation for discretely observed diffusion processes[J].Journal of the Royal Statistical Association：Series B，2006，68（ 3）：333-382.