天然气水合物输送管道气液固三相流运动特性分析

吴官纪，潘 振，陈保东，杨 帆

（辽宁石油化工大学 石油天然气工程学院, 辽宁 抚顺 113001）

随着经济的不断发展，能源问题日益凸显，石油和煤等传统的能源日益枯竭，这就要求我们寻找和探索新的可替代能源。在寻找过程中，人们发现，蕴藏在海底的天然气水合物是一种高效、清洁的可代替能源，具有相当可观的发展前景［1］。

虽然天然气水合物的储量很大，但是它通常都是储藏在海底，而且覆盖层也很浅，因此，对天然气水合物的开采和运输是天然气水合物的一个应用难题。通过探索，人们发现固态开采法是目前开采天然气水合物最有效、最合理的开采方法。在固态开采过程中，如何将天然气水合物通过水力输送技术运送至海面是最关重要的部分。因此本文利用Fluent软件对天然气水合物的竖直输送管道进行了数值模拟，对管段内部的流场特性进行了分析［2-5］。

通过模拟过程得出天然气水合物的颗粒浓度、颗粒密度、颗粒粒径以及天然气水合物输送的流速对天然气水合物的输送影响。结果表明，天然气水合物的颗粒粒径偏小、适度的体积浓度以及较小的天然气水合物颗粒密度有利于其水力输送［6,7］。

1 计算流体动力学基本控制方程

1.1 基本方程

（1）质量守恒定律

质量守恒定律是指单位时间内流体微元体中质量的变化与同一时间间隔内流入该微元体的净质量相等，方程式为：

式中：r —流体密度；

t —时间；

u、v、w —速度矢量在x、y、z方向上的分量。

（2）动量守恒定律

动量守恒定律是指微元体中流体的动量对时间的变化率与外界作用在该微元上的各种力之和相等，方程式为：

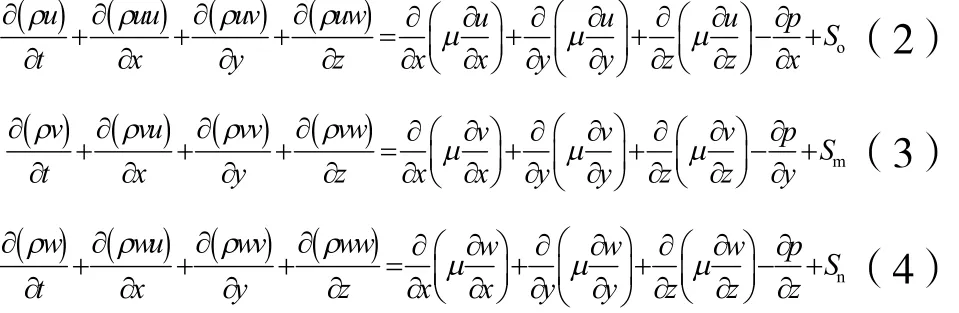
式中：u、v、w —速度矢量在x、y、z方向上的分量；

m —动力粘度；

sn、sm、s0是动量守恒定律的广义源项。

（3）能量守恒定律

能量守恒定律的定义为：微元体中能量的增加率与进入微元体的净热流量加上体力与面力对微元体所做的功相等，方程式为：

式中：T —温度；

cp—比热容；

k —传热系数；

ST—耗散项。

1.2 基本假设

为了便于利用Fluent软件模拟固、液、气三相流的流动状态，常需要做以下假设：

（1）固相天然气水合物的固体颗粒看作球形，并且假设天然气水合物的的颗粒粒径均匀大小不变。

（2)三相流中的固相是连续运动介质，液相(水)是不可压缩的流体，同时假设固液气三相的物理性质均是常数。

（3)通常认为气体为理想气体状态。

（4）流体与壁面间无滑移

1.3 三维有限元网格划分

模型网格质量的优劣对软件的计算结果的精确性及计算过程的速度起着决定性作用，因此在模拟过程中划分网格形式有重要的意义。本论文以竖直上升管道中的某一段为模拟对象，利用Fluent 软件中的 Gambit 软件开始三维模型的建立工作，在图1 中可以看到相关的三维模型。

图1 为三维模型的网格划分Fig.1 3 d model of meshing

以下是模拟过程中所需的主要几何参数 D=0.3 m, H=5 m。非结构化网格和结构化网格是构成网格总体的两部分。其中非结构化网格是指在网格区域内部相邻两点之间的毗邻单元不尽相同；而对于结构化网格则恰好相反，在网格区域内部的毗邻单元全部相同，这样建立的网格质量很好，模型网格生成效率也很高，并且利用这种网格对于区域的边界拟合过程的实现也变得相对轻松，通过使用参数化方法以及样条插值的方法对空间或者曲面进行拟合，模拟的区域较为光滑，可以接近试剂模拟的模型。

非结构化网格和结构化网格的区别在于，在计算结果的收敛性上，结构化网格形式要比非结构化网格形式优越，但是在模拟复杂的几何结构过程中，非结构化网格更具有实际的应用价值，可操作性强。在本篇论文中，笔者采用结构化网格形式建模。

1.4 边界条件

（1）进口条件：将管段底部端进口定义为速度进口边界，气液固三相的速度大小根据流量确定，并且在入口方向速度分布均匀，方向垂直于进口面，另给出湍动能、耗散率的预估值及气液固三相体积浓度及固体颗粒直径。

（2）壁面条件：所有壁面上流体都满足无滑移条件，计算时，近壁处采用标准壁面函数法处理。

（3）出口条件：将管道上端出口定义为自由出流出。

2 数值模拟结果与分析

设定天然气固体颗粒粒径为3 mm，流速为1 m/s，颗粒密度为2 000 kg/m³，体积分数为0.3，水的速度为1 m/s, 体积分数为0.4，CH4的速度为1 m/s，体积分数为0.3，考察颗粒直径对管段压力损失和阻力损失的影响，颗粒直径变化范围为3、4、5、6、7、8 mm。通过Fluent 模拟绘制出口附近水相流动速度分布云图、出口附近固、液、气流动速度分布云图、出口附近固、液气相压力分布云图、（图中以颗粒直径为3 mm为例）(图2-7)。

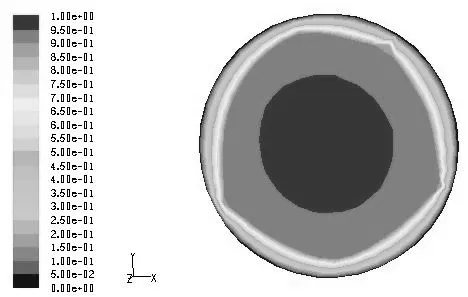
图2 出口附近气相流动速度分布云图Fig.2 Near the export gas flow velocity distribution nephogram

图3 出口附近液相流动速度分布云图Fig.3 Export liquid flow velocity distribution near the clouds

图4 出口附近气相流动速度分布云图Fig.4 Near the export gas flow velocity distribution nephogram

通过比较三者的速度变化可得随着管径的变化，三相的速度均发生变化，而固相变化的最快，管道中心的速度均为最大，但固相的变化更快且最大速度为1 m/s,而气相和液相的最大速度均超过开始速度1 m/s，通过细心地发现；气相的速度在同一点的位置要大于或等于液相的速度，由于本论文管道选取的不够长，气相的速度变化与液相的速度变化近似相等，在壁面的速度均为零，此结论完全符合流体力学及多相管流学科。

图5 出口附近固相流动压力分布云图Fig.5 Near the solid flow pressure distribution nephogram

图6 出口附近液相流动压力分布云图Fig.6 Near the liquid flow pressure distribution nephogram

由图中可以看到固液气的压力均是随着管径的变化而有规律的变化，在同一点固相压力大于液相压力，液相压力大于气相压力，不难发现三者压力呈对称状态，说明压力变化的规律可以寻找到可计算的公式，为以后的开采天然气水合物的压力分析及开采的措施应对方法提供了现实的基础。

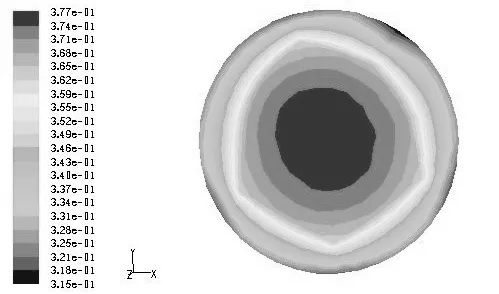
图7 为出口附近气相流动压力分布云图Fig.7 Near the gas flow pressure distribution nephogram

3 压降的计算公式及粒径对压降的影响

3.1 压降的计算公式

在海洋中开采天然气水合物的过程中，输送管道内部的固液两相流动的流动特性尚不明确，天然气水合物的颗粒的密度、颗粒粒径以及天然气水合物的体积浓度等参数设置是否符合实际开采过程中的工作还尚未确定，天然气水合物的颗粒粒径、颗粒的密度以及体积浓度等参数变化对管道输送造成的影响。

模型段管道压降

式中：pin—表示输送管道流体流进压力；

pout—输送管道流体的出口。

模型管道压力损失

式中：l0—表示所选管道的长度，m；

r —表示液体的密度。

模型管道阻力损失

式中：rm—表示混合流体的密度。

3.2 颗粒粒径对管段压力损失和阻力损失的影响

预定颗粒密度为2 000 kg/m³，颗粒体积浓度为30%，流速为1.0 m/s考察颗粒粒径对管段压力损失和阻力损失的影响，颗粒粒径的变化范围为3、4、5、6、7、8 mm。

通过图8可以发现压力损失和阻力损失都是随粒径的增大而增大的，具有正相关关系。其中压力损失与阻力损失的曲线趋近于平行。当天然气水合物的粒径在3～7 mm之间时，压力损失和阻力损失呈现出有规律的变化，粒径与压力损失可以用一条正比例关系的函数来表示。但在颗粒粒径为 8 mm时，图像函数不在是一条光滑的曲线，压力损失和阻力损失突然激增，说明当天然气颗粒直径为8 mm时，对二者损失的影响很大，是一个转折点。

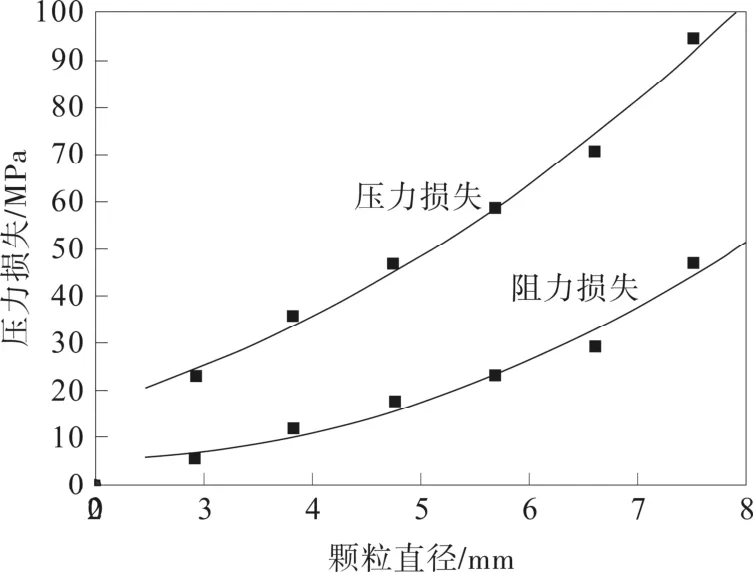
图8 为天然气固体颗粒直径与压力损失的关系Fig.8 The relationship between gas solid particle diameter and the pressure loss

4 结束语

本论文通过对天然气水合物的形成及分解条件，建立了气液固三相流的数学模型，运用质量守恒、动量守恒、能量守恒三大控制方程。在 fluent软件中，找到适合的方法，模拟了天然气水合物在竖直管道中压力、密度、速度的变化，使人们在开采的过程中能够发现更经济、更合理的开采方法。其中在选取管道时只是选取了管道长度为5 m，发现若选择的管道过长，会导致模拟结果的失败，这是美中不足之处。

随着天然气水合物颗粒直径的不断增大，管段进出口压力降也在不断增大，而且压力降增大的趋势变得不在趋于平缓，这一点可以说明，大的天然气水合物的颗粒直径有利于天然气水合物的有效输送。在粒径在3～7 mm之间的变化范围内，管段内压力损失和阻力损失的变化趋于平缓，而当粒径为8 mm 时，管段内的压力损失和阻力损失增大明显。对于输送天然气水合物的流速，管段内的压力损失随着浆体流速的升高而呈现上升趋势，管段内的阻力损失也随着浆体流速的升高而不断升高。

［1］ 周怀阳, 彭小彤, 叶瑛. 天然气水合物[M]. 北京: 海洋出版社,2000.

［2］ 史斗, 孙成权, 朱岳年. 国外天然气水合物研究进展[M]. 兰州: 兰州大学出社, 2002.

［3］ 孙志高, 樊栓狮, 郭开华, 等. 天然气水合物分解热的确定[J]. 分析测试学报, 2002, 21(3): 7-9.

［4］ 廖健, 梅东海, 杨继涛, 等. 天然气水合物相平衡研究的进展[J].天然气工业, 1998, 18(3), 75-82.

［5］ 祝道平, 宁正福. 利用高能气体压裂技术开采天然气水合物可行性分析[J]. 重庆科技学院学报(自然科学版), 2009, 11(3): 37-39.

［6］ 李淑霞, 陈月明, 杜庆军. 天然气水合物开采数值模拟的参数敏感性分析[J]. 现代地质, 2005, 19(1): 108-112.

［7］赵生才, 德国气水合物研究计划简介[J].天然气地球科学，2001,12(2), 63-67.

［8］ 马文婧;南海天然气水合物开发的风险因素分析[D].青岛：中国海洋大学,2011.