离散数学实验平台构建及实验方法研究
2015-11-13李华昱张千
李华昱+张千

摘 要 离散数学是计算机专业一门重要的基础课,在课堂讲授理论知识的同时,它的实验教学环节往往被忽视。本文结合目前离散数学课堂授课和实验教学现状,阐述了实验教学的重要性,并从实验教学模式、实验效果评价、案例教学和实验内容等方面,对提高实验教学效果的方法进行了分析与研究,并给出了具体的实现方案。
关键词 离散数学 实验教学 案例教学 实验内容
中图分类号:G642.3 文献标识码:A DOI:10.16400/j.cnki.kjdkx.2015.10.025
Experimentation Platform Construction and Method
Research of Discrete Mathematics
LI Huayu, ZHANG Qian
(College of Computer and Communication Engineering, China University of Petroleum, Qingdao, Shandong 266580)
Abstract Discrete mathematics is an important foundation course in computer science. In the course of teaching theoretical knowledge, experimental teaching is often ignored.Compared with present situation of classroom instruction and experimental teaching, this paper described the importance of experimental teaching, and from teaching mode, effect evaluation and case teaching aspects, methods of improving experimental teaching effect are analyzed and researched. Moreover,implementation scheme is also given in this paper.
Key words discrete mathematics; experimental teaching; case teaching; experimental contents
0 引言
离散数学是现代数学的一个重要分支,在计算机科学中有着极其广泛的应用,已经成为计算机科学与技术专业重要的专业基础课程。通过离散数学的学习,能够帮助学生掌握处理离散结构的描述工具和方法,为后续的“数据结构”、“数据库原理”、“操作系统”和“编译原理”等专业课程的学习创造条件,还可提高学生抽象思维和逻辑推理能力,为将来参与创新性的研究和开发工作打下坚实的基础。①
离散数学是建立在大量定义之上的逻辑推理学科,对概念、定义的理解是学习这门课程的核心。离散数学的教学内容分为数理逻辑、集合与关系、代数系统和图论四部分,涵盖了计算机科学与工程实践所需要的数学理论和方法。每一部分概念、定理繁多,都具有一定的理论抽象性,各部分之间具有一定的关联关系,既涉及具体内容,又包含思维方法。目前,由于课时限制,教师在教学过程中只重视理论教学,忽视了实验教学环节,绝大部分课时用于课堂教学,讲授抽象的定义描述和定理证明,不注意整理分散的知识点,导致部分学生认为离散数学是枯燥、如同散沙一般的课程。同时,针对离散数学的教学研究,也只侧重于教学内容探讨和理论教学方法的改进,对实践教学讨论不多。这种教学模式极大地降低了学生学习的积极性,削弱了离散数学作为计算机学科基础理论课的地位,对培养学生解决实际问题能力也起不到应有的作用。
因此,为了更好地提高离散数学教学质量,增强学生学习效果,一方面需要精选教学内容、改进教学方法;另一方面需要加强实验教学环节,通过合理的实验课时安排、上机操作和实验案例,将课堂讲授的定义、定理、性质和各个上机实验结果联系起来,使学生对抽象的理论知识有一个感性和直观的理解。
1 改进实验教学方法
1.1 构建基于网络的实验教学平台
传统的实验教学主要采用基于单机的应用模式。授课教师通过单机版实验程序进行课堂演示,或者由学生自行下载并安装实验程序,完成实验教学。在目前离散数学实验课时紧张的情况下,这种单机版应用模式使得学生只能够在有限的实验授课时才可以进行上机操作,限制了与授课教师进行交流的有效时间;此外,单纯的实验室上机环境也制约了学生学习的积极性。
随着高校实验设备、硬件设施和网络环境的不断提高与改进,为构建基于校园局域网的离散数学网络实验教学平台提供了有利条件。为此,可以将实验教学扩展为基于网络的B/S(Browser/Server)的网络实验模式。该模式打破了以往授课的时间和地域限制,学生既可在实验室进行上机操作,也可借助网络,针对特定的实验案例与教师进行在线或者离线交谈,屏蔽了教师和学生之间的地点和时间差异,使教师可以随时对学生进行在线辅导,为提高课堂教学效果提供了有效的辅助作用。
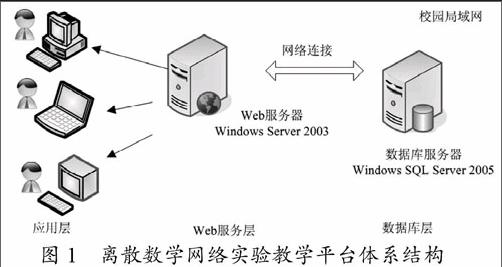
离散数学网络实验教学平台采用3层架构进行构建,如图1所示:(1)数据库服务器层:主要存储和管理实验案例的基础数据、计算分析数据和用户信息,并为其它两层提供有效的数据服务;(2)Web服务层:该层存放实验教学平台所有的实验案例程序、Web页面文件和系统配置文件,该层通过校园局域网络进行服务发布,能够及时响应并处理用户提交的实验操作请求;(3)应用层:通过分配的账号信息,学生登录网络教学平台并进入主界面;然后,根据教师布置的实验案例任务选择相关的子页面;最后,进行案例选择、模拟演示、编制程序和提交作业等操作。endprint
图1 离散数学网络实验教学平台体系结构
1.2 实验教学效果实时评价与反馈
目前,离散数学通常采用“布置任务—演示讲解—辅导”的实验教学模式,即教师首先根据课堂教学进度布置实验任务,然后对实验涉及的关键内容、操作步骤和程序设计思想进行演示和讲解,最后,安排学生上机练习,并针对若干问题对学生进行辅导。然而,教师布置任务和演示讲解会占用一定的时间,当班级学生人数较多时,没有时间和精力对每个学生进行细致的辅导,而且学生对知识的理解和接受能力往往不同,单纯通过教师的演示讲解,无法在有限的实验课时内达到较好的效果。
为此,在当前实验教学模式基础之上,需要提供有效的教学效果评价和反馈渠道,②使学生能够实时对教学效果进行实名或者匿名评价,授课教师通过对提交的评价信息进行整理与分析,发现与了解代表性和针对性强的问题,并及时将解决方法反馈给学生。这种实时评价方式可以借助网络实验教学平台进行实现,学生通过提供的效果评价功能在线提交效果评价数据,并可以及时查询教师的反馈信息,使学生能够在上课之余得到有效的辅导。
例如,针对集合论中的实验,学生可以按照自己的理解程度,从“理论知识理解”、“演示过程”、“程序设计思想”和“程序语言”四个方面选择理解困难的项目,并连同具体的问题提交到评价系统数据库中,评价结果经过汇总后,按照图2所示的方式显示提交学生的人数分布情况。借助该评价图例,教师可以直观、形象地获取量化信息,并且能够针对选定的评价项目,进一步查看具体的评价数据。
1.3 注重案例教学法
案例教学是通过具有一定典型意义的事情发生、发展的过程,使学生深刻理解理论知识的教学方法。案例教学改变以往以教师为主的课堂教学模式,更加注重学生的过程参与。通过在实践教学中引入案例教学法,引导学生运用所学定义和定理对案例进行分析讨论,不但能够开拓知识,又能活跃课堂气氛,激发学生的学习热情。
在选择实验案例时,应该注重离散数学与其它专业课程的相关性。例如:集合论中的序偶和笛卡尔积两个概念分别在《数据结构》和《数据库原理》中有所涉及,在设计该部分的实验案例时,不仅需要结合定义和定理,而且还应该让学生了解两个概念在以上课程中的应用,提高学习的针对性和目的性。为此,结合“斗兽棋”游戏进行案例设计:③“斗兽棋”共有16 颗棋子,可以看成是由A={红,蓝}、B={象,狮,虎,豹,狼,狗,猫,鼠}两个集合的笛卡尔积AB的一个子集C构成,C={<红,象>,<红,狮>,<红,虎>,<红,豹>,<红,狼>,<红,狗>,<红,猫>,<红,鼠>, <蓝,象>,<蓝,狮>,<蓝,虎>,<蓝,豹>,<蓝,狼>,<蓝,狗>,<蓝,猫>,<蓝,鼠> },每个棋子是C中的一个序偶元素,该案例能够使学生借助演示程序对序偶和笛卡尔积有具体形象的理解。关系数据模型中表结构、关系操作的查询与连接都涉及到笛卡儿积的理论,为此,还可以从数据库中的关系数据模型角度设计“笛卡儿积”的相关案例。
在设计实验案例时,不需要详细、深入地进行算法分析和代码描述,而是应该结合理论知识,侧重讲解其应用背景,使学生深刻离散数学课程的实用价值,激发自主学习的积极性。
2 实验内容设计
离散数学的实验教学内容应该依托于课堂授课内容,但不能简单地成为理论知识的教学实践。实验教学必须拓展理论教学,作为理论课的补充和加强。在设计离散数学四部分的实验教学内容时,应该从提高计算机专业学生的数学素质和程序设计能力方面出发,结合各分支的最新研究成果,以培养学生运用离散数学知识进行数学建模和解决工程应用问题的能力为目标。
针对不同的教学内容,需要设计不同类型的实验,在具体实验教学中,需要根据实验学时安排,进行选做或全做。
2.1 数理逻辑实验设计
可以从课堂授课的理论知识和实际应用领域两方面进行设计。针对计算机专业特点,安排VB或者C编程求解命题公式的真值与范式、公式等价证明和命题演算等实验,让学生进一步熟练各个联结词和等价公式的求解方法。针对数理逻辑的实际应用,可以通过高低电平表示的信号运算与二进制运算之间的联系,利用数字逻辑电路理论来设计数理逻辑方面的实验,如表决器、抢答器等电路实验。④
2.2 集合论实验设计
二元关系是集合论的主要内容,可以要求学生利用数组、向量等数据结构,采用C++、Java等编程语言实现集合的并、交、补、差等运算。此外,针对关系的自反、反自反、对称、反对称和传递五种性质判定等,进行相关的实验题目设计。⑤对于理论知识扎实和接受能力强的学生,可以进一步安排求解关系闭包和商集的算法实验。
2.3 代数结构与代数系统实验设计
代数结构与代数系统包括半群、群、环和布尔代数等概念,在密码学、通信系统等领域应用十分广泛,但具体内容非常抽象。因此,在设计实验时,应该围绕基本定义和定理,安排一些较简单的实验,例如,判断某个集合关于二元运算是否构成半群、独异点或群。同时,可以针对代数结构(下转第52页)(上接第50页)在网络信息安全中的应用,设计演示为主、练习为辅的实验,如DSA签名算法等,使学生对抽象的理论知识有一个直观的认识。
2.4 图论实验设计
图论涉及欧拉图、哈密尔顿图、平面图和树等。在设计实验时,应该结合图在计算机中的表示和运算规律,首先设计一些基础的实验内容,如求邻接矩阵和可达性矩阵等,并根据这些矩阵找出强分图、单侧分图和弱分图;然后,再针对图论的实际应用,设计与欧拉图、哈密尔顿图和树有关的编程实验,如获取城市之间最短通信路径的算法,哈夫曼编码问题等。如果课时允许,还可以设置最优二叉树构造和图的着色算法实验。
3 结束语
作为计算机专业的一门重要课程,离散数学具有理论性强和内容抽象等特性。由于离散数学课时安排紧张,课堂授课主要围绕理论知识进行讲解,很少介绍其应用背景,难以激发学生的学习兴趣。为此,需要重视实验教学环节,在实验课时有限的情况下,通过多种实验教学方法,围绕授课内容和应用领域,建立有效和可行的实验教学模式和实验内容,培养学生学习该课程的兴趣,提高离散数学教学效果。
注释
① 谭作文.离散数学课程中实验教学探讨[J].计算机教育,2010(17):106-109.
② 姜春茂,黄春梅.“离散数学”实践教学研究[J].计算机教育,2008(18):100.
③ 徐杏芳,夏浩波.案例教学法在《离散数学》中的应用[J].福建电脑,2007(7):213.
④ 郭咏梅,张剑妹.离散数学研究性实验的探索与实践[J].现代计算机,2014(24):31-33.
⑤ 钟敏,时念云.改革课程实验,提高离散数学教学质量[J].计算机教育,2008(18):29-30.endprint
