Entropy change-induced elastic softening of lithiated materials

Fuqian Yang

Department of Chemical and Materials Engineering，University of Kentucky，Lexington，KY 40506，USA

Entropy change-induced elastic softening of lithiated materials

Fuqian Yang∗

Department of Chemical and Materials Engineering，University of Kentucky，Lexington，KY 40506，USA

H I G H L I G H T S

·Effect of the stress-induced change of entropy in inlithiated materials is analyzed.

·Contribution of the change of the mixture entropy to the apparent elastic modulus is determined.

·The reciprocal of the apparent elastic modulus of a lithiated material is a linear function of the concentration of lithium atoms.

A R T I C L EI N F O

Article history：

Accepted 24 September 2015

Available online 22 October 2015

Apparent modulus Free energy

To understand the‘elastic softening''of Li-Si alloys for the development of Li-ion batteries，the effect of stress-induced change of entropy on the mechanical properties of lithiated materials is examined within the theories of thermodynamics and linear elasticity.An approach is presented whereby the change of Gibbs free energy is governed by the change of the mixture entropy due to stress-induced migration of mobile atoms，from which the contribution of the change of the mixture entropy to the apparent elastic modulus of lithiated materials is determined.The reciprocal of the apparent elastic modulus of a lithiated material is a linear function of the concentration of mobile Li-atoms at a stress-free state and the square of the mismatch strain per unit mole fraction of mobile Li-atoms.

©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/ by-nc-nd/4.0/）.

Lithium-ion batteries（LIBs）have attracted great interest for possible use as the energy supply of plug-in electric vehicles and plug-in hybrid electric vehicles［1］.In the heart of LIBs is the conversion between electric energy and chemical energy through the lithiation and de-lithiation of the active materials in electrodes during cyclic charging and discharging，which involve electrical-chemical-mechanical interaction.In general，the structural durability of LIBs is dependent on the mechanical properties of active materials at both the lithiated and de-lithiated states.

Using nanoindentation，Ratchford et al.［2，3］found Young's modulus of（52.0±8.2）GPa and（35.4±4.3）GPa for polycrystalline Li12Si7and Li22Si5，respectively，which are smaller than the Young's modulus of polycrystalline Si.Hertzberg et al.［4］，using ex-situ nanoindentation，observed Young's modulus of 12 GPa for Li15Si4.Using atomic force microscopy，McAllister et al.［5］performed in-situ nanoindentation of lithiated a-Si nanopillars and found that the mechanical properties of the a-Si nanopillars decreased with the increased degrees of lithiation and only partially recovered upon delithiation.Based on the change in substrate curvature during lithiation and de-liathiation，Sethuraman et al.［6］ found biaxial modulus of～70 GPa and～35 GPa for Li0·32Si and Li3·0Si，respectively.Using in-situ tensile test，Kushima et al.［7］obtained the stress-strain curves of lithiated Si-nanowires，which showed the Young's modulus of the lithiated Si-nanowires is less than that of virgin Si-nanowires.

Shenoy et al.［8］performed a first-principles calculation for both amorphous and crystalline phases observed during the lithiation of Si anodes，and their results showed that the homogenized modulus of crystalline Li-Si phases decreases with increasing Li concentration，qualitatively in accord with the trend observed by Ratchfordetal.［2，3］fromthenanoindentationtests.Usingtheparticle swarm optimization method in conjunction with ab initio calculations，Cui et al.［9］showed the transition from disordered to ordered states of Li-Si crystalline structures and the decrease of elastic modulus of Li-Si phases with increasing Li concentration. Considering the contribution of solute atoms to the Helmholtz free energy of solid solution，Yang［10］derived a linear relationship between Young's modulus and the concentration of solute atoms. However，none of them has discussed the ordering effect on the change of apparent elastic modulus，while the lithiation-induced migration of mobile（excess）atoms has been observed in various materials，including graphene［11］and TiO2［12］.

In general，there exists an interaction between lithium migration and mechanical stress during electrochemical cycling ofLIBs［10，13］，which has been the base for the analysis of the stress evolution in the active materials of electrodes.It is expected that external stresses can introduce the re-distribution of mobile Li-atoms in lithiated materials，which can alter the mechanical behaviorofthelithiatedmaterials.Itisthepurposeofthisworktoanalyze the change of thermodynamic energy and mechanical strain due to stress-induced distribution of mobile Li-atoms.

Fig.1.Schematic of the uniaxial tension of a lithiated material.

Consider that a lithiated material in a shape of rectangular prism is subjected to uniaxial tensile stress，as shown in Fig.1.The distribution of mobile Li-atoms in the lithiated material is random and disorder at a stress-free state，and the deformation is elastic and infinitesimal.Under the condition of a constant applied stress，σ，in the z-direction，the Gibbs free energy，G，per unit volume can be written as

Here，U is the internal energy of the material per unit volume，T is temperature，S is entropy per unit volume，andεis tensile strain.

For the internal energy，there is

Using Eq.（2），the increment of the Gibbs free energy of G can be expressed as

Under the condition that the concentration of mobile Li-atoms，c0（in the unit of per mole of material），remains unchanged during elastic deformation，tensile strain can be calculated as

withεerepresenting the contribution from elastic deformation，andεcrepresenting the strain due to the presence of mobile Liatoms in the lithiated material.The elastic strain is expressed as

and the strain due to the presence of mobile Li-atoms as

Here，E isYoung'smodulus，χisthelinearstrainperunitmolefraction of mobile Li-atoms，c0is the concentration of mobile Li-atoms at the stress-free state，andΔc is the change of the local concentration of mobile Li-atoms induced by the tensile stress.The term χΔc represents the strain due to the re-distribution（repositioning）of mobile Li-atoms induced by the tensile stress.

Similar tothe mismatchstrain，theconstantχcanbecalculated as

with a being the average distance between atoms（lattice constant）.Substituting Eqs.（5）and（6）into Eq.（4）yields

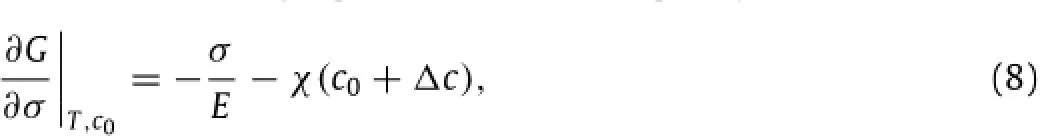
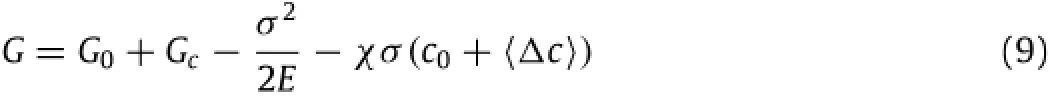
which gives with G0+Gcbeing the thermodynamic energy per unit volume of the material without the deformation and〈Δc〉being the average change of the local concentration of mobile Li-atoms under the action of the stress.Here，G0is independent of the concentration of mobile Li-atoms，and Gc（=-TΔsm；smis the entropy of mixture）represents the contribution of the change of the entropy of mixture.

The change of the entropy of mixture can be calculated by following the method used in the analysis of rubber elasticity［14］. In general，mobile Li-atoms can only occupy limited positions（sites）in an active material，such as interstitial sites in crystalline materials，e.g.lithiated silicon，lithiated graphite，etc.Assume that there are N0sites available for mobile Li-atoms in x-direction per mole of lithiated material，N0is Avogadro's constant.Introduce the concentrations of the mobile Li-atoms in x-，y-，and z-sites as cx，cy，and cz.At the stress-free state，there is cx=cy=cz≡c0with cx+ cy+cz=3c0.The number of total configurations，N，in which the mobile Li-atoms occupy the x-，y-，and z-sites can be calculated as

Using the Boltzmann equation，one obtains the entropy of mixture at the stress-free state，as

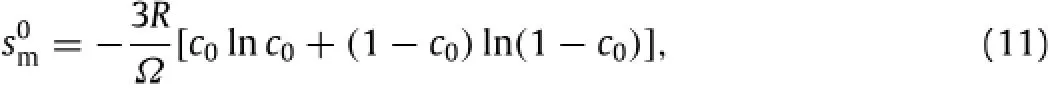
where R is the gas constant andΩis the molar volume.

It is known that there exists an interaction between atomic migration and mechanical stress［15-17］.External mechanical loading will cause the migration and re-distribution of mobile Li-atoms in the lithiated material.Under the action of the tensile stress，the average concentration of mobile Li-atoms in the z-direction becomesc0+〈Δc〉，i.e.cz=c0+〈Δc〉.Consideringmassconservation and the isotropic feature in the xy plane，one obtains the concentrationofmobileLi-atomsinthex-andy-directionsasc0-〈Δc〉/2，i.e.cx=cy=c0-〈Δc〉/2.Following the same approach in deriving Eq.（11），one obtains the entropy of mixture under the action of the tensile stressas

inwhichtheapproximationofln（1-y）≈y+y2/2wasused.From Eqs.（11）and（12），the change of the entropy of mixture under the action of the tensile stress is calculated as

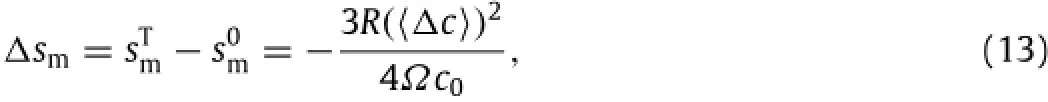
which gives Gcas

Both the change of the entropy of mixture and the change of the Gibbs energy are inversely proportional to the equilibriumconcentration of mobile Li-atoms in the lithiated material at the stress-freestateandproportionaltothesquareofthechangeofthe concentration of mobile Li-atoms in the z-direction induced by the tensile stress.

According to Eq.（6），the strain due to the stress-induced repositioning of mobile Li-atoms is determined by the parameter χandthelocalchangeoftheconcentrationofthemobileLi-atoms. It is known that，under the action of the tensile stress，mobile LiatomswillmigrateintheactivematerialuntiltheGibbsfreeenergy reaches minimum at an equilibrium state.At the equilibrium state，there is

SubstitutingEq.（14）intoEq.（9）andusingEq.（15）yieldthechange of the equilibrium concentration of mobile Li-atoms，〈Δce〉，under the action of the tensile stress as

According to Eqs.（4）-（6），one can find the resultant strain，εr，of the rectangular prism under the action of the tensile stress as

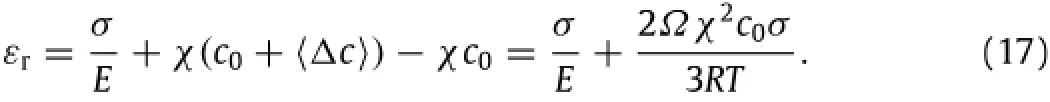
Define the apparent elastic modulus，Eapp，as

which is found as

Obviously，the presence of mobile Li-atoms in active materials can introduceelasticsofteningduetothestress-inducedredistribution of mobile Li-atoms，which is qualitatively in accord with the observation by McAllister et al.［5］.

Consider a lithiated material of LizX.The concentration of mobile Li-atoms in X is c0.Using the relationship between volumetric strain and linear strain，the linear strain of the LizX material due to the presence of the mobile Li-atoms can be expressed as

with VLizX（0）being the volume of the lithiated material without any mobile（excess）Li-atoms and VLizX（c0）being the volume with the mobile（excess）Li-atoms.Assuming that the linear strain is the strain induced by the presence of the mobile Li-atoms，one obtains

Substituting Eq.（21）in Eq.（19）yields

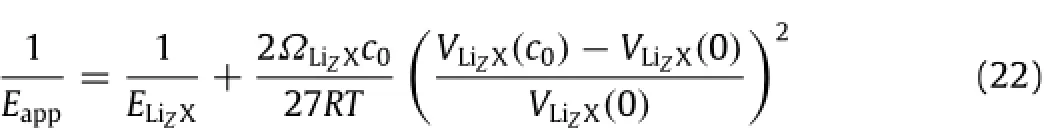
for the calculation of the apparent elastic modulus of the material ofLizXasafunctionoftheconcentrationofmobileLi-atoms，which is due to the deformation-induced change of entropy.This result suggests that the concentration dependence of elastic constants in lithiated materials during charging and discharging likely is associated partially with the entropy change induced by the stressinduced migration of mobile Li-atoms.

For a dilute solution of a lithiated material with small specific dilation induced by mobile（excess）Li-atoms，there is

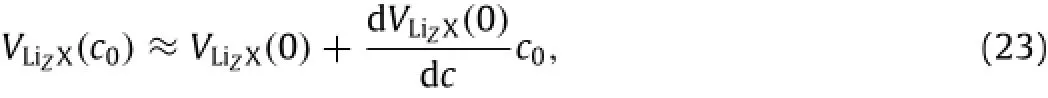
which gives

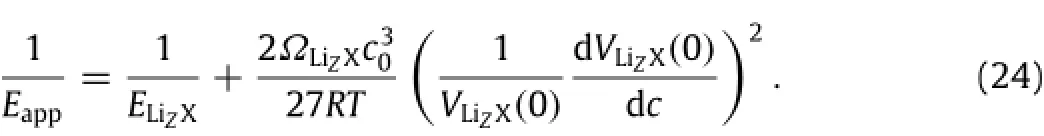
In summary，the variation of the mechanical properties of lithiated materials during charging and discharging is associated with the microstructural change induced by mobile Li-atoms.The stress-induced migration of mobile Li-atoms causes the change of thermodynamic functions，resulting in the change of elastic modulus.The work presented here has attempted to bring out the potential importance of the stress-induced change of entropy in lithiated materials in determining the variation of mechanical properties with lithiation and de-lithiation.In particular，the study has shown that the reciprocal of the apparent elastic modulus of a lithiatedmaterialisalinearfunctionoftheconcentrationofmobile Li-atoms at the stress-free state and the square of the mismatch strain per unit mole fraction of mobile Li-atoms，as introduced by the mobile Li-atoms in the material.

［1］A.A.Pesaran，G.H.Kim，M.Keyser，Integration issues of cells into battery packs for plug-in and hybrid electric vehicles，in：EVS-24 Intern.Battery，Hybrid and Fuel Cell Electric Vehicle Symp.，Stavanger，Norway，2009.

［2］J.B.Ratchford，B.A.Crawford，J.Wolfenstine，et al.，Young's modulus of polycrystalline Li12Si7using nanoindentation testing，J.Power Sources 211（2012）1-3.

［3］J.B.Ratchford，B.E.Schuster，B.A.Crawford，et al.，Young's modulus of polycrystalline Li22Si5，J.Power Sources 196（2011）7747-7749.

［4］B.Hertzberg，J.Benson，G.Yushin，Ex-situ depth-sensing indentation measurements of electrochemically produced Si-Li alloy films，Electrochem. Commun.13（2011）818-821.

［5］Q.P.McAllister，K.E.Strawhecker，C.R.Becker，et al.，In situ atomic force microscopy nanoindentation of lithiated silicon nanopillars for lithium ion batteries，J.Power Sources 257（2014）380-387.

［6］V.A.Sethuraman，M.J.Chon，M.Shimshak，et al.，In situ measurement of biaxial modulus of Si anode for Li-ion batteries，Electrochem.Commun.12（2010）1614-1617.

［7］A.Kushima，J.Y.Huang，J.Li，Quantitative fracture strength and plasticity measurements of lithiated silicon nanowires by in situ TEM tensile experiments，ACS Nano 6（2012）9425-9432.

［8］V.B.Shenoy，P.Johari，Y.Qi，Elastic softening of amorphous and crystalline Li-SiPhaseswithincreasingLiconcentration：Afirst-principlesstudy，J.Power Sources 195（2010）6825-6830.

［9］Z.W.Cui，F.Gao，Z.H.Cui，et al.，A second nearest-neighbor embedded atom method interatomic potential for Li-Si alloys，J.Power Sources 207（2012）150-159.

［10］F.Q.Yang，Diffusion-inducedstressininhomogeneousmaterials：concentration-dependent elastic modulus，Sci.China Phys.Mech.55（2012）955-962.

［11］V.A.Sethuraman，L.J.Hardwick，V.Srinivasan，et al.，Surface structural disordering in graphite upon lithium intercalation/deintercalation，J.Power Sources 195（2010）3655-3660.

［12］D.N.Wang，L.J.Liu，X.L.Sun，et al.，Observation of lithiation-induced structural variations in TiO2nanotube arrays by X-ray absorption fine structure，J.Mater. Chem.A 3（2015）412-419.

［13］F.Q.Yang，Effectoflocalsolidreactionondiffusion-inducedstress，J.Appl.Phys. 107（2010）103516.

［14］D.V.Ragone，Thermodynamics of Materials，John Wiely&Sons，Inc.，New York，1995.

［15］F.Q.Yang，Interactionbetweendiffusionandchemicalstresses，Mater.Sci.Eng. A-Struct.409（2005）153-159.

［16］F.Q.Yang，J.C.M.Li，Diffusion induced beam bending in hydrogen sensors，J. Appl.Phys.93（2003）9304-9309.

［17］P.Zuo，Y.P.Zhao，A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries，Phys.Chem.Chem.Phys.17（2015）287-297.

10 September 2015

∗Tel.：+1 859 2572994；fax：+1 859 3231929.

E-mail address：fyang2@uky.edu.

http：//dx.doi.org/10.1016/j.taml.2015.09.003

2095-0349/©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/by-nc-nd/4.0/）.

Entropy change

Lithium-ion battery

*This article belongs to the Biomechanics and Interdiscipline