Combined modeling of cell aggregation and adhesion mediated by receptor-ligand interactions under shear flow

Yu Du，Shuang Peng，Yuhong Cui，Shouqin Lü，Yan Zhang，Mian Long，∗

aCenter of Biomechanics and Bioengineering，Institute of Mechanics，Beijing 100190，China

bKey Laboratory of Microgravity（National Microgravity Laboratory），Institute of Mechanics，Beijing 100190，China

cBeijing Key Laboratory of Engineered Construction and Mechanobiology，Institute of Mechanics，Beijing 100190，China

dDepartment of Mechanics，Tianjin University，Tianjin 300072，China

Combined modeling of cell aggregation and adhesion mediated by receptor-ligand interactions under shear flow

Yu Dua，b，c，Shuang Penga，b，c，Yuhong Cuid，Shouqin Lüa，b，c，Yan Zhanga，b，c，Mian Longa，b，c，∗

aCenter of Biomechanics and Bioengineering，Institute of Mechanics，Beijing 100190，China

bKey Laboratory of Microgravity（National Microgravity Laboratory），Institute of Mechanics，Beijing 100190，China

cBeijing Key Laboratory of Engineered Construction and Mechanobiology，Institute of Mechanics，Beijing 100190，China

dDepartment of Mechanics，Tianjin University，Tianjin 300072，China

H I G H L I G H T S

·Combine the dynamics of cell aggregation and adhesion under shear flow.

·Parametric analysis of cell collision and adhesion efficiency.

·Interplay between cell aggregation and adhesion near the wall.

A R T I C L EI N F O

Article history：

6 September 2015

Accepted 29 September 2015

Available online 23 October 2015

Cell adhesion Aggregation Kinetics Shear flow

Blood cell aggregation and adhesion to endothelial cells under shear flow are crucial to many biological processessuchasthrombiformation，inflammatorycascade，andtumormetastasis，inwhichthesecellular interactionsaremainlymediatedbytheunderlyingreceptor-ligandbindings.Whiletheoreticalmodeling ofaggregationdynamicsandadhesionkinetics ofinteractingcellshavebeenwellstudiedseparately，how to couple these two processes remains unclear.Here we develop a combined model that couples cellular aggregation dynamics and adhesion kinetics under shear flow.The impacts of shear rate（or shear stress）and molecular binding affinity were elucidated.This study provides a unified model where the action of a fluid flow drives cell aggregation and adhesion under the modulations of the mechanical shear flow and receptor-ligand interaction kinetics.It offers an insight into understanding the relevant biological processes and functions.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：// creativecommons.org/licenses/by-nc-nd/4.0/）.

Blood cell aggregation and adhesion to endothelial cells under shearflowarecrucialtomanybiologicalprocessessuchasthrombi formation，inflammatorycascade，andtumormetastasis.Forexample，homotypic aggregation of activated platelets induced by high shear stress or by chemokines is involved in many diseases such as atherosclerosis and thrombosis［1］while heterotypic aggregation between platelets and neutrophils（PMNs）is responsible for thrombosis progression［2］and acute myocardial infarction［3］.In inflammatorycascade，flowingPMNsadheretotheendotheliumof post-capillaryvenuletomediatethesequentialtransmigrationand phagocytosis at the target site［4］.Tumor cells also interact with leukocytes in blood flow，e.g.，between PMNs and melanoma cells［5-8］orcoloncarcinomacells［9，10］，tofacilitatetumormetastasis.

Homotypic or heterotypic aggregation of blood cells is mainly governed by blood flow and binding kinetics of interacting molecules.A body of experimental evidence，via flow chamber assay and cone-plate viscometer［11，12］，demonstrates that shearinducedaggregationofPMNsandtransfectedcellsisshear-ratedependent［12］.The underlying cellular adhesive molecules，e.g.，β2integrinandintercellularadhesivemolecule1（ICAM-1），isfoundto playakeyregulatingrole［5］.Ontheotherhand，theoreticalmodels basedonpopulation balanceequation［13］havebeendevelopedto test the size distribution of cell aggregates and predict the aggregation dynamics in a uniform shear field for homotypic aggregation of human blood platelets［14］or PMNs［13，15］，as well as for heterotypic aggregation of platelets and PMNs［16］or PMNs and tumor cells［5］.Noting that these measurements and models are referred to as the flow field in a free stream of a blood vessel，the impact of presence of endothelium monolayer on cell aggregation as well as cell adhesion mediated by the interactions of blood cells and endothelial cells should be taken into account.

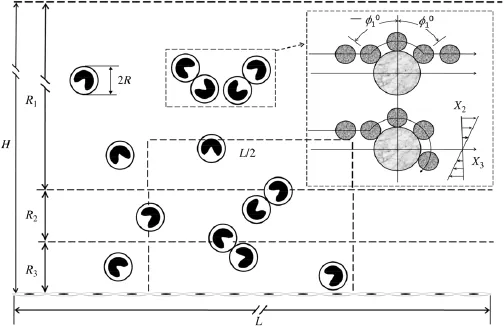
Fig.1.Schematic of cell aggregation and adhesion under shear flow.Cell aggregation and adhesion occur in a chamber of 20（L）×1·0（H）mm，in which three regions，R1，R2，and R3with a height of 0.96，0.02，and 0.02 mm are considered separately.R indicates the cell radius assumed to be a sphere.

Cell-cellinteractionsbecomemorecomplicatedwhentheflowing cells are marginalized to the vicinity of the endothelium.In addition to the similar dynamics of shear-induced aggregation of blood cells arising in free stream，the marginalized cells occasionally collide with the endothelium and result in rolling over，tethering onto，and crawling along endothelial cells.Again，cell adhesion and detachment are governed by binding kinetics of interacting molecules under shear flow.For instance，PMNs or beads bearing selectin and/or integrin receptors are driven to flow over the ligand-immobilized or—expressed substrate or cells and the shear stress dependence of rolling velocity，tether rate，and‘stop-andgo''frequency have been determined experimentally using a flow chamberassay［17，18］.Usinga（gas-driven）micropipetteadhesion assay，notonlyadhesiondynamicsbetweenthetwocellsisquantified but binding kinetics of the receptor-ligand interactions is also determinedunderzeroforce.Bycontrast，theoreticalmodelsofcell adhesion have been developed，as observed that cell adhesion is governed by cell margination from free stream，cellular Brownian motion and molecular diffusion near endothelium，and binding kinetics of two contact molecules［19］.Evidently，these models are different from those for cell aggregation in free stream，since the endothelial cells are lined stably as a monolayer.

Although cell aggregation and adhesion dynamics are well studied separately，their integration under blood flow has been poorly understood.Here we develop a model to combine both the cell aggregation in free stream and the cell adhesion in the vicinity of the endothelium.Using two-body collision theory and a binding kinetics model for a small system，the impacts of shear flow and bindingkineticsofinteractingmoleculesareanalyzed.Comparison of the predictions with measured data validates our model.

As shown in Fig.1，‘blood flow''in a chamber with a length of L and a height of H is segregated into three regions：Region 1（R1）denotes the body flow along the main stream with a height of r1，where‘blood cells''are able to collide freely with each other and form aggregates；Region 2（R2）is referred to as the transient flow with a height of r2，where the cells are close to but do not interact with vessel wall；Region 3（R3）represents the local flow with proximity to the blood vessel with a height of r3，where the cells are able to contact with the wall and induce cell adhesion.

In a two-dimensional（2D）Couette flow along X3-axis with a flow velocityv=G×X2，sphere collision occurs due to the velocity gradient or shear rate，G.Based on Smoluchowski two-body collision theory in colloidal dynamics［13］，the collision frequency depends on sphere concentration C，shear rate G，and sphere radius R（inset in Fig.1）.In the case of uniformly distributed spheres，two-body collision frequency per unit volume，f，in the threedimensional（3D）case，f=16R3GC2/3，is simplified as the value per unit area in the 2D case：

The two-body collision brings the spheres into contact and provides the opportunities for surface-presented receptors and ligands to bind with each other.Supposing two spheres collide atis the initial contact angle；inset in Fig.1）in a mirror-image manner，which is a so-called transient doublet.Yet the doublet will remain attached under hydrodynamic force until all the bonds break up，which is named a non-separating doublet.

For a transient doublet rotating from，the contact duration，τ，is given by：

It is known that shear flow applies a normal force（FN= αNηR2Gsin2θ1sin2φ1）and a shear force（FS=αSηR2G［（cos2θ2cosφ2）2+（cosθ2sinφ2）2］1/2）to the doublet，whereαNandαSare force coefficients as a function of the dumbbell geometry andηis the medium viscosity［13］.Noting that shear force FSis neglected as it has little effect on the break-up of the doublet［13，19］，the applied force yields in the 2D case，

To predict the fate of existing bonds in a doublet so formed，a probabilistic model based on small system kinetics［20］is developed，which describes the binding kinetics of a small number of receptor-ligand bonds，n（1，2，3，···，N，where N is the maximum number of bonds able to be formed between two spheres）［5，19，21，22］：

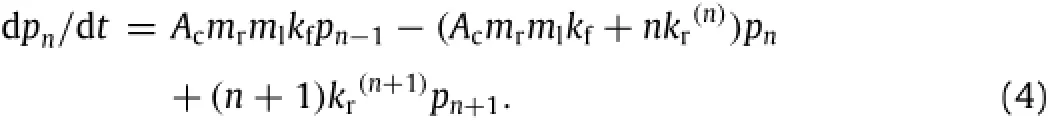
Here，pnis the probability of having n bonds at time t，mrand mlare the respective site densities of receptors and ligands，kr（n）and kfaretherespectivereverseratefornthbondandforwardrate，andAcis the contact area between two spheres.Adhesion probability，Pa，yields 1-p0，indicating that at least one bond is formed to link two spheres.

Table 1 Typical parameter values for numerical calculations.a

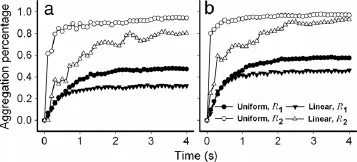
Fig.2.Time course of aggregation percentage，defined as the ratio of number of doublets to the total number of spheres at that moment in a centered box of 10×0·02 mm in the regions of body flow（R1）（closed points）and transient flow（R2）（open points）.

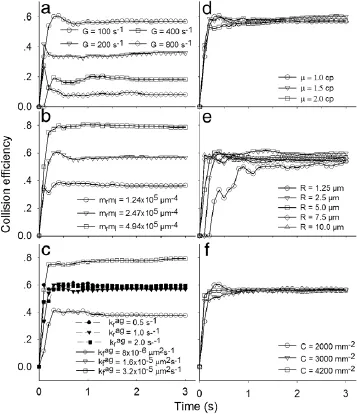
Fig.3.Parametric analysis of（a）shear rate，（b）site densities and（c）forward rate（solidpoints）orreverserate（openpoints）ofinteractingmolecularpair，aswellas（d）medium viscosity，（e）sphere radius and（f）concentration on aggregation dynamics in R1.Collision efficiency is defined as the effective number of collision for doublet formation divided by the total number of collision.

External forces are found to affect the dissociation of receptor-ligand bonds，which is so-called mechano-chemical coupling effect.In an existing model，kr（n）is assumed to be a function of the applied force，F，that is equally shared by the number of bonds，n［23］.It is formulated as an exponential force dependence of reverse rate， whereis the zero-force reverse rate，a the bond interaction range，kBthe Boltzmann constant，and T the absolute temperature.

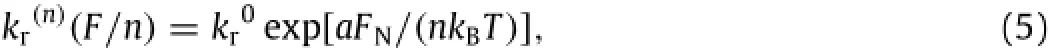
FLUENT 6.3.26 is used to solve the Navier-Stokes equation，and the aggregation and adhesion dynamics is integrated into computational fluid dynamics（CFD）by user defined files.The modeling parameters and validation are described in the Supplemental Materials（see Appendix A）.

Twoinitialinjectionsettingsareused，onehasuniforminjection probability（cycles）and the other presents the linearly increased probability along y-axis（triangles）at two bulk concentrations of spheres of C0=4200 and 8000 mm-2（plots（a）and（b）in Fig.2）.Other parameters are given in Table 1.The results indicated that the aggregation percentage exhibits a transition phase followed by an equilibrium plateau.Specifically，sphere aggregation is lower in R1（solid points）than that in R2（open points）at low（4200 mm-2）（Fig.2（a））or high（8000 mm-2）（Fig.2（b））bulk concentration（Fig.2），indicating that the spheres appearing in free stream are able to form less doublets presumably due to the high velocity in R1.Considering that there exist various types of blood cell distributions when the cells flow from one blood vessel to another，we test the impacts of two typical injection settings at the inlet.One yields a uniform and the other has a linearly increased probability for spheres injected along the yaxis，on sphere aggregation（also on adhesion later on）in the fully developed regimes.As exemplified in Fig.S3，the inverse distribution of sphere population along y-axis was observed upon uniform injection since the spheres at large y values readily flow away at higher velocity（Fig.S3（a）），whereas the linear injection results in the uniform bulk distribution of spheres along the y-axis（Fig.S3（b））.Thus，as shown in Fig.2，the uniform injection（cycles）induces the higher aggregation than that from linear injection（triangles）at two bulk concentrations，mainly due to the large number of spheres at small y values.Interestingly，it was also found that the time course of sphere aggregation exhibits a slight fluctuation in R2in both uniform and linear injection settings（Fig.2），suggesting that the interplay between R2and R1and/or even R3may be critical.

Next，we test the effects of shear rate，site densities and kinetic rates of interacting molecules，as well as medium viscosity，sphere radius and concentration on collision efficiency，defined as the effective number of collisions for doublet formation divided by the total number of collision.Spheres are injected with a linearly increased probability and forced to flow over the substrate.Here the parameters are given in Table 1 except of those indicated otherwise.On one hand，the efficiency decreases significantly with increase of shear rate mainly due to the shorter contact duration at the higher shear rate，as seen in Eq.（2）（Fig.3（a））.It increases remarkably with increase of site densities and becomes highly stableuponthemasstransportationlaw（Fig.3（b））.Italsoincreases with forward rate（open symbols）but not reverse rate（closed symbols）before the first bond is formed（Fig.3（c））.Note that data points at（open triangles）are invisible due to being overlaid by those for reverse rates（closed symbols）.On the other hand，the three parameters of medium viscosity（Fig.3（d）），sphere radius（Fig.3（e））and concentration（Fig.3（f））do not affect much the sphere aggregation.Independence of viscosity implies that the efficiency is shear rate（instead of shear stress）dependent.Independence of sphere radius and concentration suggests that the efficiency is free of sphere size and number，as described previously［19］where the terms of R and C0will be canceled out when calculating the efficiency from Eq.（1）.Notably，high fluctuation and low efficiency are observed for smallest sized spheres probably due to the low volume fraction over the entire system.It is also indicated that the efficiency exhibits initially a short transition phase（＜1.0 s for sphere radius and＜0.5 s for other five parameters）.Thus，these analyses profile the parametric dependence of sphere aggregation mediated by receptor-ligand bonds in free stream or R1.

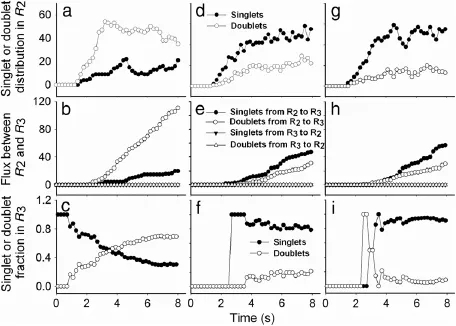
Fig.4.Singlet（closed points）and doublet（open points）distributions in R2and R3and their interplays across the two regions.Time courses of instantaneous number（1st row），cumulative flux（2nd row），and instantaneous fraction（3rd row）of singlets or doublets at time t were obtained in a centered box of 10×0·02 mm2in R2.

Not only are the interplays between R1and R2crucial to sphere aggregation in free stream，but those between R2and R3are also important in regulating sphere adhesion to the substrate.Here we further calculate the population of sphere singlets and doublets andthefluxofspheresacrosstheinterfacebetweenR2andR3.With alinearinjectionsettingandasphereconcentrationof4200mm-2，thetimecourseoffractionofspheresingletsanddoubletsinR2was obtained in a centered box with a dimension of 10×0·02 mm2（cf.Fig.1），where the box length L/2 is selected for analyzing the distribution in the fully developed flow regime and the height r2is chosen to have at least one doublet presenting in the box.Three sets of forward and reverse rates were used in=0·8×10-5The other parameters were given in Table 1.As exemplified in Fig.4（a），the instantaneous number of singlets at time t exhibits a transition phase when t＜4 s followed by a fluctuation up to t=8 s，while the number of doublet also presents a transition phase when t＜2·4 s followed by a descending phase up to t=8 s.Moreover，the singlet number（closed points）is lower than that for doublets（open points），implying that more doublets are formed in R2at pre-set kinetic rates ofThis predominant population of doublets is reversed when reducingto a half alone，where the singlet number is higher than the doublet（Fig.4（d）），and would be further turned over when additionally enhancing kagrto 10-fold high，where the singlet number quickly approaches the plateau（t＜2·0 s；Fig.4（g））. It is also noted that the late-phase fluctuation observed in R2is different from the saturation visualized in R1（Figs.2 and 3），presumably due to the non-negligible interplays between R2and R3.It is worth noting that the fluctuation observed from the time courses is probably attributable to the stochastic nature of sphere aggregation dynamics.

To further test the possible impacts of their interplays，the flux of spheres across the interface between R2and R3was also calculated，in which the cumulative flux is defined as the number of singlets or doublets crossing over the interface up to time t within the box.As presented in Fig.4（b），the flux for both singlets and doublets flowing from R2into R3（cycles）exhibits a quiescent phase and then increases with time，indicating that the spheres are forced to move to the vicinity of the substrate.At a given time，the doublet flux（open points）is higher than that of singlets（closed points），which is consistent with the data shown in Fig.4（a）.Again，such is the predominant transportation of doublets reversed by reducing the forward rate（Fig.4（e））and enhancing the reverse rate（Fig.4（h））.By contrast，almost no cell singlets or doublets were found to flow from R3back into R2（overlaid triangles in 2nd row），suggesting that those spheres having presented in R3are unlikely to re-enter R2.Instead，they tend to either adhere onto the substrate or flow out within the limits of R3.

Accordingly，we further calculate the instantaneous fraction of singlets or doublets，presenting in R3at time t，in an ensemble of total spheres.As shown in Fig.4（c），the singlet fraction（closed points）declines but the doublet fraction（open points）increases with time，since fewer singlets but more doublets are imported from R2（Fig.4（b））.By contrast，the singlet or doublet fraction would not alter much with time when reducing the forward rate（Fig.4（f））and enhancing the reverse rate（Fig.4（i）），regardless of their initial fluctuation phases.These results suggest that the time courseofsingletordoubletfractionmainlydependsontheforward rate or the reverse rate used.

Spheres presenting in R3are able to attach and then adhere to the substrate.Without loss of generality，a distinct set of kinetic parameters，andis used to solve Eqs.（2）-（5）and then predict the adhesion dynamics of spheres to the substrate.Three sets of forward and reverse rates were used in（3rd column）.The other parameters were given in Table 1.It was found that the cumulative number of attachments or detachments up to time t is enhanced with time，in which the attachment occurrence is higher than the detachment at the given kinetic rates（Fig.5（a））.Such a difference is lowered when the forward rateis reduced to a half，in that the attachment occurrence is lowered to about a half while the detachment occurrence remains the same（as seen in Fig.5（d））. Furthermore，the difference between attachment and detachment is even eliminated（overlaid cycles）when the reverse rateis enhanced 10-fold，resulting in much higher occurrence in both attachment and detachment（Fig.5（g））.This is because there are more spheres which，having detached from the substrate at high，would not bounce back into R2（Fig.4），but re-attach to the substrate again.

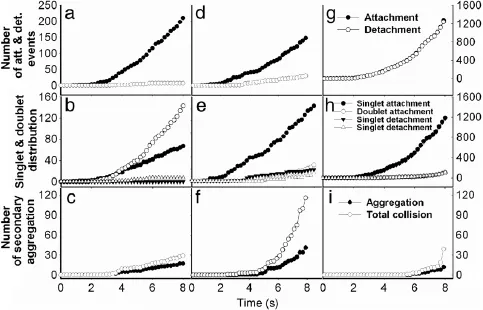
Fig.5.Adhesion dynamics of spheres to the substrate with a linearly increased injection probability.Time course of cumulative number（1st row），number of attached（open points）and detached（closed points）singlets（cycles）or doublets（triangles）（2nd row），and number of secondary doublet-forming events（closed points）or total number of secondary collision events（open points）（3rd row），were obtained in a centered box of 10×0·02 mm2in R3.The y-axes for the panels g and h are scaled separately.

Fig.6.Parametric analysis of（a）contact duration，（b）site densities and（c）forward rate（solid points）or off-rate（open points）of interacting molecular pair，as well as（d）shear rate，（e）sphere radius and（f）concentration on adhesion efficiency in R3. Adhesion efficiency is defined as the effective number of attachment for sphere adhesion divided by the total number of attachment.

We also refine the singlet or doublet attachment and detachment occurrences withinCorresponding with the kinetic rates used in Fig.5（a），（d），and（g），attachment is much higher for the doubletthanthesingletbothofwhicharesignificantlyhigherthan the respective detachments（Fig.5（b））.This situation is sharply altered whenis reduced to a half，where the singlet attachment and detachment are higher than the respective values for doublets（Fig.5（e））.Moreover，the singlet events are predominant when 10-fold highis applied additionally，resulting in the overlaid attachment（cycles）and detachment（triangles）events，respectively，for singlets（closed symbols）and doublets（open symbols）（Fig.5（h））.

We further test the secondary aggregation for an adhered singlet interacting to a freely-flowing singlet.Here the adhesion of a doublet having formed in free flow onto endothelium has been excluded，since such a doublet generally lasts too short a time（in a scale of sub-seconds）to survive at late phase，which hardly supports the recruitment to and the adhesion on the endothelium［19］.Bycountingthenumberofsecondarydoublet-formingevents and total number of secondary collision events，it is found that the secondary aggregation does not occur until t=2·9 s（Fig.5（c）），3.2 s（Fig.5（f）），and 5.8 s（Fig.5（i）），implying that the occurrence is rare at the early phase on the three sets of kinetic rates.Beyond that moment，it increases with time.The final collision efficiency at t=8·0 s，defined as the ratio of these two numbers，yields values of 0.59，0.37，and 0.30，respectively，suggesting that the secondary aggregation is no longer negligible at the late phase. This observation indicates that the majority of collisions of flowing spheres within R3tend to induce secondary aggregates，and it is crucial in understanding the interplays between sphere adhesion and aggregation.

Moreover，we test the effects of contact duration，site densities and kinetic rates of interacting molecules，as well as shear rate，sphere radius and concentration on adhesion efficiency，defined as the effective number of attachment for sphere adhesion divided by the total number of attachment.Spheres are injected with a linearly-varied probability and forced to flow over the substrate.Here the parameters are given in Table 1 except of those indicated otherwise.On one hand，the results indicate that the longer the contact duration（Fig.6（a）），the higher the site densities（Fig.6（b）），and the higher the forward rate（open points）（Fig.6（c）），the higher the efficiency in different contents.The reverse rate，however，seems not to affect the adhesion significantly（closed points）（Fig.6（c））.Note that data points at=1·65× 10-5µm2·s-1（open triangles）are invisible due to being overlaid by those for reverse rate（closed symbols）.It is also noted that，as compared to the analysis for sphere aggregation（Fig.3），the high fluctuation was found in the time courses here，presumably due to the stochastic nature of the small system of adhering spheres.On the other hand，the time course dramatically fluctuates at the early phase and tends to reach the similar plateau at systematically variedshearrate（Fig.6（d）），sphereradius（Fig.6（e））andconcentration（Fig.6（f））.Note that the small sized spheres（R=1·25 and 2·5µm）would not yield the reasonable adhesion efficiencies（Fig.6（f）），similar to those observations in sphere aggregation（Fig.3（d））.

Finally，the present work，by combining sphere aggregation dynamics with sphere adhesion kinetics within a Couette flow framework，simulates two aspects of cell behavior：the impact of blood flow on cell aggregation in free stream and cell adhesion in the vicinity of the endothelium.Our work furthers the understanding of the biological processes of cell-cell and cellendothelium interactions mediated by underlying receptor-ligand binding under physiological flows in large blood vessels.In the smaller microvessels，the laminar flow can still be achieved upon the low Reynolds number but the drag force would be greatly affected by aggregated or adhered cells.

Acknowledgments

This work was supported by National Natural Science Foundation of China（grants 31230027，31110103918 and 11172207），NationalKeyBasicResearchFoundationofChina（grant 2011CB710904），and Strategic Priority Research Program（grants XDA01030102 and XDA04020219）.

Appendix A.Supplementary material

Supplementary material related to this article can be found online at http：//dx.doi.org/10.1016/j.taml.2015.09.004.

［1］C.Gachet，Regulation of platelet functions by P2 receptors，Annu.Rev. Pharmacol.Toxicol.46（2006）277-300.

［2］T.Palabrica，R.Lobb，B.C.Furie，etal.，Leukocyteaccumulationpromotingfibrin deposition is mediated in vivo by P-selectin on adherent platelets，Nature 359（1992）848-851.

［3］F.J.Neumann，N.Marx，M.Gawaz，et al.，Induction of cytokine expression in leukocytes by binding of thrombin-stimulated platelets，Circulation 95（1997）2387-2394.

［4］F.W.Luscinskas，M.I.Cybulsky，J.M.Kiely，et al.，Cytokine-actived human endothelial monolayer support endhanced neutrophil transmigration via a mechanism involving both endothelial-leukocyte adhesion molecule-1 and intercellular-adhesion molecule-1，J.Immunol.146（1991）1617-1625.

［5］S.Liang，C.Fu，D.Wagner，et al.，Two-dimensional kinetics of beta（2）-integrin andICAM-1bindingsbetweenneutrophilsandmelanomacellsinashearflow，Am.J.Physiol.Cell Physiol.294（2008）743-753.

［6］P.Zhang，T.Ozdemir，C.-Y.Chung，et al.，Sequential binding of alpha（v）beta（3）and ICAM-1 determines fibrin-mediated melanoma capture and stable adhesion to CD11b/CD18 on neutrophils，J.Immunol.186（2011）242-254.

［7］M.J.Slattery，S.Liang，C.Dong，Distinct role of hydrodynamic shear in leukocyte-facilitated tumor cell extravasation，Am.J.Physiol.Cell Physiol.288（2005）831-839.

［8］S.Liang，M.J.Slattery，C.Dong，Shear stress and shear rate differentially affect the multi-step process of leukocyte-facilitated melanoma adhesion，Exp.Cell Res.310（2005）282-292.

［9］S.Jadhav，B.S.Bochner，K.Konstantopoulos，Hydrodynamic shear regulates the kinetics and receptor specificity of polymorphonuclear leukocyte-colon carcinoma cell adhesive interactions，J.Immunol.167（2001）5986-5993.

［10］S.Jadhav，K.Konstantopoulos，Fluid shear-and time-dependent modulation of molecular interactions between PMNs and colon carcinomas，Am.J.Physiol. Cell Physiol.283（2002）1133-1143.

［11］N.A.Turner，J.L.Moake，L.V.McIntire，Blockade of adenosine diphosphate receptors P2Y（12）and P2Y（1）is required to inhibit platelet aggregation in whole blood under flow，Blood 98（2001）3340-3345.

［12］E.R.Hentzen，S.Neelamegham，G.S.Kansas，et al.，Sequential binding of CD11a/CD18 and CD11b/CD18 defines neutrophil capture and stable adhesion to intercellular adhesion molecule-1，Blood 95（2000）911-920.

［13］M.von Smoluchowski，Experiments on a mathematical theory of kinetic coagulation of coloid solutions，Z.Phys.Chem.92（1917）129-168.

［14］R.D.Guy，A.L.Fogelson，Probabilistic modeling of platelet aggregation：Effects of activation time and receptor occupancy，J.Theoret.Biol.219（2002）33-53.

［15］P.Tandon，S.L.Diamond，Kinetics of beta（2）-integrin and L-selectin bonding during neutrophil aggregation in shear flow，Biophys.J.75（1998）3163-3178.

［16］I.J.Laurenzi，S.L.Diamond，Monte Carlo simulation of the heterotypic aggregation kinetics of platelets and neutrophils，Biophys.J.77（1999）1733-1746.

［17］C.Zhu，T.Yago，J.Z.Lou，et al.，Mechanisms for flow-enhanced cell adhesion，Ann.Biomed.Eng.36（2008）604-621.

［18］R.Alon，S.Q.Chen，K.D.Puri，et al.，The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling，J.Cell Biol.138（1997）1169-1180.

［19］M.A.Long，H.L.Goldsmith，D.F.J.Tees，et al.，Probabilistic modeling of shearinduced formation and breakage of doublets cross-linked by receptor-ligand bonds，Biophys.J.76（1999）1112-1128.

［20］D.A.McQuarrie，Kinetics of small systems 1，J.Chem.Phys.38（1963）433-436.［21］S.E.Chesla，P.Selvaraj，C.Zhu，Measuring two-dimensional receptor-ligand binding kinetics by micropipette，Biophys.J.75（1998）1553-1572.

［22］C.L.Fu，C.F.Tong，C.Dong，et al.，Modeling of cell aggregation dynamics governed by receptor-ligand binding under shear flow，Cell Mol.Bioengineer. 4（2011）427-441.

［23］G.I.Bell，Models for specific adhesion of cells to cells，Science 200（1978）618-627.

［24］T.Yago，V.I.Zarnitsyna，A.G.Klopocki，et al.，Transport governs flow-enhanced cell tethering through L-selectin at threshold shear，Biophys.J.92（2007）330-342.

［25］D.A.McQuarrie，Kinetics of small systems 1，J.Chem.Phys.38（1963）433-436.

［26］S.I.Simon，H.L.Goldsmith，Leukocyte adhesion dynamics in shear flow，Ann. Biomed.Eng.30（2002）315-332.

20 July 2015

at：Center of Biomechanics and Bioengineering，Institute of Mechanics，Beijing 100190，China.

E-mail address：mlong@imech.ac.cn（M.Long）.

http：//dx.doi.org/10.1016/j.taml.2015.09.004

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/by-nc-nd/4.0/）.

in revised form

*This article belongs to the Biomechanics and Interdiscipline