Effects of humidity on shear behavior of bamboo

Sin Askrinejd，Peter Kotowski，Fezeh Shlhy，Nim Rhr，，∗

aDepartment of Mechanical Engineering，Worcester Polytechnic Institute，Worcester，MA，USA

bDepartment of Civil and Environmental Engineering，University of Massachusetts，Dartmouth，MA，USA

cDepartment of Civil and Environmental Engineering，Worcester Polytechnic Institute，Worcester，MA，USA

Effects of humidity on shear behavior of bamboo

Sina Askarinejada，Peter Kotowskib，Faezeh Shalchyc，Nima Rahbara，c，∗

aDepartment of Mechanical Engineering，Worcester Polytechnic Institute，Worcester，MA，USA

bDepartment of Civil and Environmental Engineering，University of Massachusetts，Dartmouth，MA，USA

cDepartment of Civil and Environmental Engineering，Worcester Polytechnic Institute，Worcester，MA，USA

H I G H L I G H T S

·A functionally graded orthotropic model of bamboo is proposed.

·Bamboo with 60%environmental humidity demonstrated the highest shear modulus.

·The optimal humidity of the samples for highest strength is between 60%-80%.

·Similar to wood，bamboo，a grass，exhibitsmoreductilityundertorsion as the humidity of the samples increases.

A R T I C L EI N F O

Article history：

Accepted 14 November 2015

Available online 28 November 2015

Bamboo

Torsion test

Humidity

Finite element analysis

G R A p H I C A LA B S T R A C T

Bambooisanaturallyoccurringbiologicalcomposite，howeveritsmicrostructureandhenceitsproperties are very complex compared to the manmade composites.Due to optimization，it can be assumed that the variation in properties along the thickness of the culm be a smooth transition for better bonding strength between layers and to prevent non uniformity in stress concentration.As a consequence，biological structures are complicated and functionally graded.Hence，a realistic model that can capture the mechanical performance of bamboo is valuable in future design of robust multifunctional composites. This paper presents the results of experimental and numerical studies on the torsional（shear）properties of bamboo.The hierarchical and multi-scale structure of bamboo and the distribution of micro-scale fibers are revealed via laser scanning and atomic force microscopy.This information was incorporated into a finite element model to analyze the mechanical behavior of bamboo under torsion and to estimate the shear modulus of bamboo along the fibers.Moreover，the effects of humidity and therefore water content on the mechanical properties of bamboo were evaluated by performing torsion tests on samples maintained in environments with different humidities.Increasing the humidity does not cause a drop in the shear modulus，however，a jump in the shear modulus did occur at around 60%humidity.Results of this study indicate that the highest strength values in samples occurred in environments with humidity levels between 60%and 80%and undergo a significant drop after that.In higher humidities，the samples behave more ductile.

©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/ by-nc-nd/4.0/）.

Bamboo is one of the oldest building materials used by mankind.There are signs in far east，for instance，where Chinese writings and drawings refer to bamboo that date back from 1600 BCto100BC［1，2］.Bamboohasbeen usedtofabricatestructuralelementsandalsoasanalternativetosteelinreinforcedconcrete［3］. Sustainability and the practice of using environmentally friendlymaterials is continually gaining momentum in both developed and underdeveloped parts of the world［4-6］.This is largely due to the decreasing supply of available timber around the world.Natural materials all around us exhibit fascinating properties that are typically multifunctional and optimal for the construction purposes［7］.Bamboo is a very favorable sustainable material for the construction industry.Bamboos attractive combination of strength-to-weight ratios，stiffness-to-weight ratios，and shape factors make it an ideal candidate for construction materials and many other applications［5-11］.

Most bamboo culms are cylindrical and hollow，with diameters ranging from 0.25 in.to 12 in.（1 in.=2.54 cm）.Bamboo is considered a composite made up of non-uniformly distributed longitudinal fibers［12-14］.Separating the culms are evenly spaced nodes with internal diaphragms（knots）.The main constituents of bamboo culms are cellulose，hemicellulose and lignin，which amount to over 90%of the total mass［15-18］.The minor constituents of bamboo include resins，tannins，waxes and inorganic salts.As an orthotropic material，the density of the bamboo changes through the cross-section，ranging from 500 kg/m3to 800 kg/m3，with the higher density located at the outside face. Theuniquefiber-matrixratioanddistributiongivebambooexceptional strength characteristics［19-21］.To prevent non-uniformity in stress concentration and increase bonding strength between layers，the variation in the properties along the thickness of the culm should be modeled using a smooth transition［22-24］.There are many variables that affect the strength of bamboo，including maturity，season when it is harvested，and the treatment applied after the bamboo harvest.Previous studies have shown that the optimum maturity period is about 3-4 years to provide optimum strength［25］.Following this period of time the strength and density of bamboo begins to decay.At the optimum maturity period，bamboohasshowntensilestrengthsgreaterthanspruceandequal to or greater than steel per unit weight.

Few studies treating the modeling of natural fibers have been found in the literature due to the complexity of the microstructure［14，26］.However，there are many experimental studies on bamboo measuring strength，Young's modulus of matrix and fiber，and through the analysis of its microstructure and fiber distribution［20，26-34］.In a study of Dixon and Gibson（2014）［8］，the flexural properties of Moso bamboo in the axial direction，along with the compressive strengths in the axial and transverse directions were measured，and based on the microstructural variations and extrapolated solid cell wall properties of bamboo，analytical models which describe the experimental results were developed. Another approach used to estimate how the microstructure influences the effective properties of bamboo is to model these materials through the use of homogenization，or the extraction of the microstructure properties that can then be introduced to the section as a whole［35-37］.Employing a homogeneous，averaged value of Young's modulus can also be used，allowing comparisons and demonstrating the limitations of simplified procedures.However，considering that bamboo has complicated shapes and materialdistributioninsideitsdomainwithmanyimportantdetails，the numerical methods such as the finite element method（FEM）can be useful tools for understanding the mechanical behavior of these functionally graded materials（FGMs）［9，27-30，38-41］and many composite structures in general［42，43］.Molecular dynamics（MD）is another effective tool to study the properties of composite materials［18，44，45］.

In spite of its structural application，there have been no prior mechanistic studies on the role of water content with regard to the mechanical performance of bamboo.Many studies have been conducted on other biological materials such as nacre and bone. As an example，the existence and role of water in the structure of nacre has been investigated by many researchers.It has been mentioned that the effect of water acts to increase the ductility of nacre and increase the toughness［46，47］.The conductivity of bamboo and effect of absorbed water was investigated in a study conducted by Shiji et al.［48］.However，more multiscale investigation is needed to understand the effect of water content or humidity on the mechanical performance.

The goal of this study is to experimentally and numerically investigate the mechanical behavior of bamboo in torsion.While other studies have estimated the modulus and stiffness，very few studies have investigated the torsional properties and shear modulus of bamboo.In this study a new method of modeling was used to estimate the shear modulus of bamboo.Additionally，the effect of humidity on the torsional behavior of bamboo was investigated. Theresultsofthisstudycanbeusedasaguidetoimprovetheproperties of bamboo in different applications，take advantage of effect of water on natural materials，and to design and make bioinspired composites with remarkable mechanical properties.

Samples from the Phyllostachys species of bamboo were used for the torsional experiments conducted in this study.The bamboo samples were approximately five years old.The bamboo was kiln dried and stored in a ventilated warehouse for at least a year followed by storage within the lab.The storage assured that only gradual moisture changes took place and ensured that cracks in the bamboo did not form prior to testing.The experiment in torsion was conducted using a Tinius Olsen Model 290 torsion testing machine（Fig.1）with a maximum torque of 10000 lb·in（1lb=0.454kg）.Theonboardloaddisplaywasbypassedwiththe use of LabView software platform with a custom written program to record load，rotation，and strains.Two fixtures were fabricated outofmildsteelwithsix3/8in.-24threadboltsineachforsecuring the bamboo sample.

Kiln dried Phyllostachys bamboo was cut to 14 in.in length.The specific length of 14 in.was chosen due to the limitation of the testing machine having a maximum specimen length of 20 in.in addition to the bamboo node spacing.With the specimen having a nodespacingofapproximately12in.，thefittingscouldbeclamped within one inch of a node on each end of the 14 in.specimen.The average diameter of the bamboo was about 2.25 in.with a 1/4 in. wall thickness.

An important factor in a torsion experiment is to prevent slippage between the specimen and the fixture for accurate rotation recordings measurements.Preliminary tests of the fixture system resulted in the bolts slipping on the bamboo surface at a torque of approximately 800 lb·in.Additional tightening of the bolts would pose additional damage to the specimen and larger concentrated loads at the location of the bolts.As a result，a new system was developed by precisely drilling 9/32 in.holes where the fitting bolts would normally meet with the bamboo.A series of one inch wide washers bent to the outside curvature of the bamboo along with 3/4 in.washers bent to the inside curvature are used in conjunction with 1/4 in.bolts and matching nuts，one inch in length to create the mounting setup.In addition，80 grit drywall sandpaper was sandwiched between the outside washer and bamboo to provide increased friction.A completed bamboo specimen setup is shown in Fig.1.

By orientating the bolt heads parallel to the longitudinal fiber direction，the heads can bear the applied transverse load.The specimen was mounted into the fitting with the fitting bolts tightenedontothewashersandbearingonthebolthead.Usingthe 9/32in.holethroughthebambooandlargewashersdistributedthe load evenly and prevents excessive concentrated loads at the hole locations.Using the setup，the experiment proved to be successful with no slippage and failure occurring in between the mounting holes，showing that excessive concentrated loads are not taking place at the holes.Loading occurred at five degrees per minute until the specimen reached failure.Throughout the experimentload（torque）and rotation were recorded at a rate of 5 data points per second.

Fig.1.（a）Experimental setup.（b）Fixtures（grit drywall sandpaper，bolts and matching nuts）that were used to secure the bamboo sample during the torsion test.

Fig.2.Bamboo cross section image taken using laser scanner and the 2D and 3D AFM images of the bamboo fibers.

Figure 2 shows the structures of bamboo as scanned using a laser scanner.This image shows bamboo structure consisting of bundles of vascular fibers in a matrix of parenchyma cells.Most significantly，themesostructureishighlygradedinthatthevolume fraction of the fibers in the bamboo culm increases from inside to outside，the latter being the part that is exposed to the atmosphere or environment.The high fiber density region，low fiber density regionandthemediumfiberdensityregion（in-betweenthesetwo regions）can be seen in the image.The microstructural features of the fiber bundles were also studied here by means of an atomic force microscope（AFM）.Samples were polished with a 4000 grit sand paper to a 1µm surface finish.Later，the surface roughness of the samples was studied with an AFM in the tapping mode.2D and 3D images are captured and shown in Fig.2.

To understand the effect of water content on the shear behavior of bamboo，samples were prepared and kept in theenvironments with different humidities.The humidities were set to 25%，40%，60%，80%，and 100%.The samples were cut from the same parts of the bamboo stalks.Five samples for each humidity were tested and the torque-rotation curves were obtained.The humidity was controlled in a moisture and temperature chamber where the humidity was set to a constant value.A high precision programmable constant temperature and humidity chamber（Vision Scientific Co.LTD，South Korea）was used.Samples remained in the chamber for 48 h，removed and immediately tested.

Fig.3.The 3D meshed model and the assigned material orientation used to implement the orthotropical mechanical behavior.

Table 1 Materials properties of the constituents in bamboo mesostructure.

3D finite element simulations were performed to extract the shear properties of the samples assuming orthotropic mechanical behavior.Four-node tetrahedron elements were used to mesh the model（Fig.3）.A total of 151381 elements and 679949 nodes were used to analyze the finite element model.

The material properties of the fiber and matrix used to find the components of the orthotropic stiffness tensor are presented in Table 1.Fiber volume fractions as a function of thickness were calculated from the laser scanning measurements.The laser scanning images were used to count the number of fibers per unit length as a function of the distance from the outer layer of bamboo.Later，the general rule of mixtures for composites was applied to estimate the actual graded elastic properties of bamboo microstructure as a function of thickness［49］.Orthotropy is the property of a point within an object rather than for the property of the object as a whole.Bamboo is both orthotropic and inhomogeneous which means it possesses orthotropic properties that vary from inside to outside layers.

The simulations were performed in two steps.In the first step，the distribution of fiber was implemented into the model.The gradientofstiffnessfrominsidelayertooutsidelayerwasassumed to be linear［30］.Therefore，two different sets of orthotropic properties，onefortheinsidelayerandtheotheronefortheoutside layerweresufficienttodefinethepropertiesofthebulkmodel.The properties presented in Table 1，the orientation of the fibers in the parenchymacell，andtheorthotropicpropertiesoftheparenchyma cell itself were used to define the stiffness tensor of the bamboo model in torsion.The second step was to apply the torsion load on the sample and compute the rotations from the results as the other end is fixed in all directions and rotations.

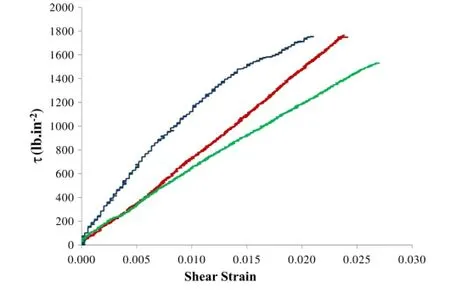
Fig.4.The shear stress-shear strain curve of the bamboo specimens computed from the torsion experiment with 25%environmental humidity.

The raw data（torque-rotation）of the torsion experiments on different samples were obtained.Since，the measurement of total strain field of a heterogeneous orthotropic material is difficult，and the finite element results showed that the behavior of a dry sample（environmental humidities less than 25%）can be reasonably approximated as a linear orthotropic material，this behavior was assumed to compute the stress strain curves for all samples.Theslopeofthesecurvesintheearlystageofdeformation is the average shear modulus.The typical shear stress-shear strain curve for the torsion experiment on samples kept in an environment with 25%humidity is presented in Fig.4.All the 25 humidity samples show a similar linear behavior under torsion. The shear strength of these samples is approximately 1700 lb/in2.

Figure 5 shows a fractured sample under torsion.It was observed that the crack did not start from the fixture bolts on the sample.Hence，it proves that the test setup was successfulin applying pure torque on the sample and in preventing stress concentration around the bolts.

Table 3 Comparison between shear modulus found by FEM and experiments.

Fig.5.The samples under torsion tests were not fractured from the holes. This proves that the test setup is successful in eliminating the effect of stress concentration around the holes.

The shear modulus of bamboo was computed using finite element analysis and the prescribed experimental data.The general rule of mixtures was assumed to be able to implement the mechanical properties of bamboo into the model.The compliance matrix，S，used for the inside and outside layers is as follows： The nine components of the compliant tensor needed to define the compliance matrix for the inside and outside layers are computed by considering the volume fraction of fibers in the inner and outer layers of bamboo.The properties of the outer layer and inner layer are listed in Table 2.

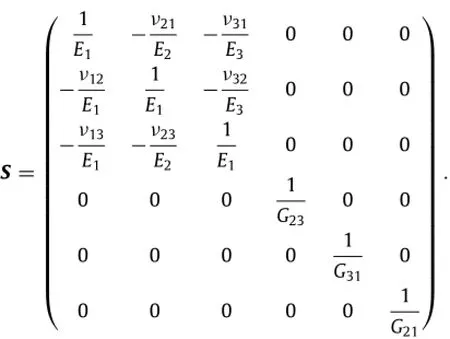
These numbers can be extracted from the numbers presented in the Table 1 and the rule of mixtures for composites in different directions assuming 80%fibers for outer layer and 20%fiber for the inner layer and the rest are parenchyma-cells.E1is the modulus in R direction which assumed to be the same as E2which is the modulus inθdirection and E3is the modulus along the fibers（Z direction）.The properties of an average wood（mainly made of parenchyma-cells）can be used to find the shear moduli in inner and outer layers.The compliant tensor is then defined and implementedintothefiniteelementmodel.Figure6（a）showshow the distribution of stiffness in the system，which increases from inside to outside layers.The stiffness gradient is assumed to be linear in the model［9］.Figure 6（b）shows the maximum principle stressdistributionofthebamboosampleundertorsion.Findingthe compliant tensor for samples in higher environmental humidities requires knowledge of the mechanical properties of bamboo fibers and parenchyma cell with different water contents.Hence，the proposed numbers apply for the bamboo samples prepared in low environmental humidity（under 25%）.

These simulations are used to estimate an average shear modulus of the bamboo.In order to find the shear modulus，a specific amount of rotational deformation was applied to one side of the model while the other side was fixed.The reaction torque that appears in the fixed side can be used to find the average shear modulus.The following equation which only applies for isotropic materials was used to find the average shear modulus（G）.The geometry of the model should be used to find the torsional rigidity（J）：whereθis the angle of twist，T is the torque or moment，L is the length of the model and J is the torsion constant for the section，and G is the average shear modulus.

The numerical simulation results agree well with experimental data as it is shown in Table 3.This shows that the proposed modeling approach is correct for a dry（25%environmental humidity）bamboo sample using the available data on the mechanical properties of bamboo fiber and matrix.Modeling the samples with higher humidity requires more information about thepropertiesofbamboofibersandparenchymacellwithdifferent watercontents.Theslightdifferencebetweentheexperimentsand numerical results is perhaps due to vast variety in the mechanical properties of the fibers and matrix of different bamboo samples. While，all bamboo sample have the same age and were prepared under the same protocol，there is still a variety of properties from samples to sample.

The goal of this study is to understand the effect of environmental humidity on the shear modulus and shear strength of bamboo samples.The raw data（torque-rotation）of the torsion experiments of samples with different environmental humidities are presented in Fig.7.Assuming the homogeneous isotropic behavior，the shear stress-shear strain curves from experimental data for the samples are calculated and presented in Fig.8.The slope of these curves at the early stage of deformation is the average shear modulus and can be compared for samples prepared in different environmental humidities.

The results indicate that as the humidity（water content）increases，thefailureshearstrainofthebamboosamplesincreases. Moreover，the shear stress-shear strain curves show a softening region due to the increased humidity.The samples with humidity level of 25%and 40%behave linearly，while samples with 60%-100%humidity behave nonlinearly，since humidity increases the softening behavior of bamboo.The samples with 25%humidity show a failure strain of around 0.028，while，the samples with 40%and 60%humidity show a failure strain of around 0.045，and samples with 80%and 100%humidity show a failure strain of around 0.056.The effects of humidity on the ultimate strength ofthe samples are presented in Fig.9.The results clearly show that there is an optimum environmental humidity between 60%and 80%that causes the highest shear strength in bamboo.Moreover，increase in humidity beyond 80%，causes a significant drop of the ultimate strength.

Table 2 Components of complaint tensor considered in the finite element model for inside and outside layers.

Fig.6.（a）Gradient of stiffness in the cross section of the bamboo model.（b）Maximum principle stress distribution in the sample after the application of torsion.

Fig.7.The torque-rotation curves obtained from torsion experiment on bamboo specimens prepared in 25%to 100%environmental humidity.

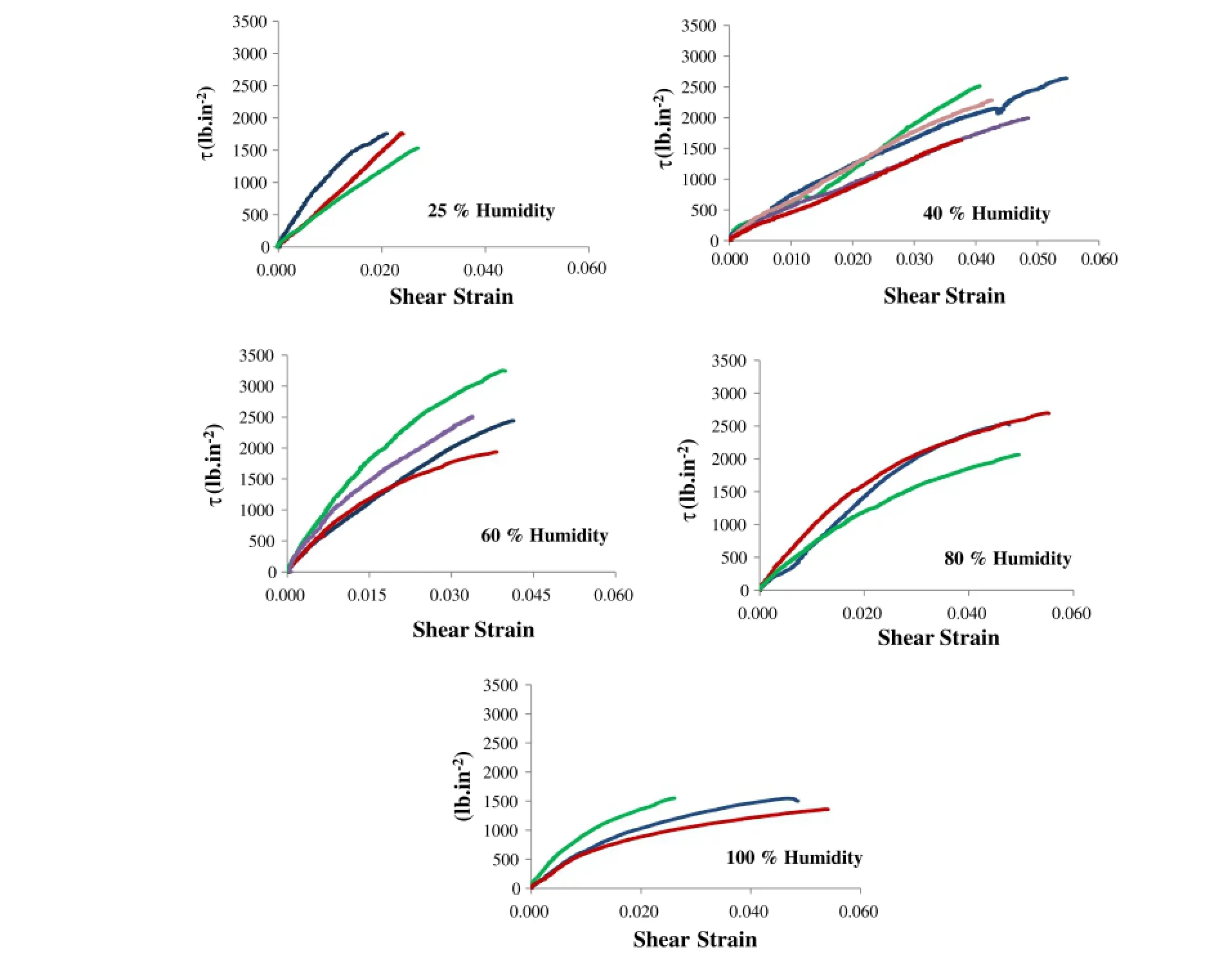
Fig.8.The shear stress-shear strain curves of the bamboo specimens computed from the torsion experiment with 25%to 100%environmental humidity.

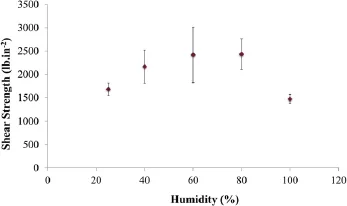
Fig.9.Effect of humidity on the ultimate strength of the samples.The error bars show the standard deviation of the experimental results.

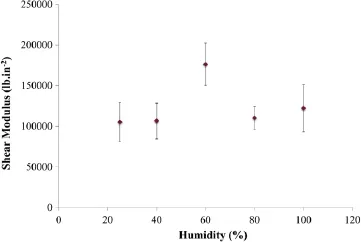
Fig.10.Effect of humidity on the shear modulus of the samples.The error bars show the standard deviation of the experimental results.

Figure 10 presents the effect of humidity on the shear modulus of the samples.The results show that there is a small jump in the shearmodulusofbambooatenvironmentalhumidityofabout60%，otherwise，all other samples show almost similar shear stiffness of about 100000 psi.

This study presents the results of experimental and numerical studies on the torsional behavior of bamboo，a natural functionally graded composite material with remarkable mechanical properties.Since water content plays an important role on mechanical properties of natural materials，the experimental part of this study focused on the effect of humidity on the performance of bamboo samples under torsion.Finite element analysis was used to model bamboo under torsion as a heterogeneous orthotropic material with linear distribution of fiber across the section.The shear modulus found from the numerical analysis is consistent well with the experimental data which shows that the finite element analysis can be used as a tool to estimate an average shear modulus of the samples.The overall results also show that bamboo kept in an environment with humidity level of 60% demonstrated the highest shear modulus.The optimal humidityof the samples for highest strength is between 60%and 80%.The results show that bamboo exhibits more ductility under torsion as thehumidityofthesamplesincreases.Theresultsofthisstudyprovide crucial information on the role of water on the optimal shear strength of bamboo.This information is essential in understanding the role of water on mechanical properties of bamboo fiber and matrix.

Acknowledgment

N.Rahbar is truly grateful for support from the National Science Foundation（NSF）Faculty Early Career Development Program（CAREER）（Grant No.1261284）.

［1］D.Yu，H.Tan，Y.Ruan，A future bamboo-structure residential building prototype in China：Life cycle assessment of energy use and carbon emission，Energy Build.43（2011）2638-2646.

［2］T.Y.Lo，H.Z.Cui，P.W.C.Tang，et al.，The effect of fiber density on strength capacity of bamboo，Constr.Build.Mater.22（2008）15325.

［3］H.G.Geymayer，F.B.Cox，Bamboo reinforced concrete，ACI J.Proc.67（10）（1970）.

［4］N.Sathitsuksanoh，Z.Zhu，T.J.Ho，et al.，Special issue on lignocellulosic bioethanol：current status and perspectives，Bioresour.Technol.101（2010）49264929.

［5］K.Ghavami，Bamboo as reinforcement in structural concrete elements，Cem. Concr.Compos.27（2005）63749.

［6］Y.Xiao，Q.Zhou，B.Shan，Design and construction of modern bamboo bridges，J.Bridge Eng.15（2010）53341.

［7］S.Askarinejad，N.Rahbar，Toughening mechanisms in bioinspired multilayered materials，J.R.Soc.Interface 12（2015）20140855.

［8］P.G.Dixon，L.J.Gibson，The structure and mechanics of Moso bamboo material，J.R.Soc.Interface 11（2014）20140321.

［9］T.Tan，N.Rahbar，S.M.Allameh，et al.，Mechanical properties of functionally graded hierarchical bamboo structures，Acta Biomater.7（2011）37963803.

［10］X.Huang，A.Netravali，Biodegradable green composites made using bamboo micro/nano-fibrils and chemically modified soy protein resin，Compos.Sci. Technol.69（2009）1009-1015.

［11］J.J.A.Janssen，Bamboo in building structures（Ph.D.thesis），Technische Hogeschool Eindhoven，Eindhoven，1981.

［12］M.K.Habibi，Y.Lu，Crack propagation in bamboos hierarchical cellular structure，Sci.Rep.4（2014）55985604.

［13］I.Low，Z.Che，B.Latella，Mapping the structure，composition and mechanical properties of bamboo，J.Mater.Res.21（2006）19691976.

［14］E.C.N.Silva，M.C.Walters，G.H.Paulino，Modeling bamboo as a functionally graded material：lessons for the analysis of affordable materials，J.Mater.Sci. 41（2006）6991-7004.

［15］L.Zou，H.Jin，W.Y.Lu，et al.，Nanoscale structural and mechanical characterization of the cell wall of bamboo fibers，Mater.Sci.Eng.，C.29（2009）13751379.

［16］U.G.Wegst，H.Bai，E.Saiz，etal.，Bioinspiredstructuralmaterials，NatureMater. 14（2015）2336.

［17］A.N.Fernandes，L.H.Thomas，C.M.Altaner，et al.，Nanostructure of cellulose microfibrils in spruce wood，Proc.Natl.Acad.Sci.108（2011）11951203.

［18］S.Youssefian，N.Rahbar，Molecular origin of strength and stiffness in bamboo fibrils，Sci.Rep.5（2015）11116.http：//dx.doi.org/10.1038/srep11116.

［19］K.Ghavami，Ultimate load behaviour of bamboo-reinforced lightweight concrete beams，Cem.Concr.Compos.17（1995）281-288.

［20］S.C.Lakkad，J.M.Patel，Mechanical properties of bamboo，a natural composite，Fibre Sci.Technol.14（1981）319-322.

［21］T.Y.Lo，H.Z.Cui，H.C.Leung，The effect of fiber density on strength capacity of bamboo，Mater.Lett.58（2004）2595-2598.

［22］S.Suresh，A.Mortensen，Fundamentals of Functionally Graded Materials，IOM Communications，London，1988.

［23］G.H.Paulino，Z.-H.Jin，R.H.Dodds Jr.，in：B.Karihaloo，W.G.Knauss（Eds.），Comprehensive Structural Integrity，Vol.2，Elsevier，2003，p.607.

［24］J.J.A.Janssen，Mechanical Properties of Bamboo，Kluwer Academic Publishers，Dordrecht，1991.

［25］A.C.Sekhar，R.K.Bhartari，Studies on strength of Bamboos：a note on its mechanical behaviour，Indian For.86（1960）296-301.

［26］X.S.Bai，A.W.C.Lee，L.L.Thompson，et al.，Finite element analysis of Moso bamboo-reinforced southern pine OSB composite beams，Wood Fiber Sci.31（1999）403.

［27］F.Nogata，H.Takahashi，Intelligent functionally graded material：Bamboo，Compos.Eng.5（1995）743-751.

［28］S.Amada，T.Munekata，Y.Nagase，etal.，Themechanicalstructuresofbamboos in viewpoint of functionally gradient and composite materials，J.Compos. Mater.30（1996）800-819.

［29］S.Amada，R.S.Lakes，Viscoelastic properties of bamboo，J.Mater.Sci.32（1997）2693-2697.

［30］S.Amada，Y.Ichikawa，T.Munekata，etal.，Fibertextureandmechanicalgraded structure of bamboo，Composites B 28（1997）13-20.

［31］S.Amada，S.Untao，Fracture properties of bamboo，Composites B 32（2001）451-459.

［32］S.H.Li，Q.Y.Zeng，Y.L.Xiao，et al.，Biomimicry of bamboo bast fiber with engineering composite materials，Mater.Sci.Eng.C 3（1995）125-130.

［33］N.Nugroho，N.Ando，Development of structural composite products made from bamboo II：fundamental properties of laminated bamboo lumber，J.Wood Sci.47（2001）237-242.

［34］A.W.C.Lee，X.S.Bai，A.P.Bangi，Flexural properties of bamboo-reinforced southern fine OSB beams，For.Prod.J.47（1997）74-78.

［35］E.Sanchez-Palencia，Non-Homogeneous Media and Vibration，in：Theory Lecture Notes in Physics，vol.127，Springer，Berlin，1980.

［36］M.H.Santare，J.Lambros，Use of graded finite elements to model the behavior of nonhomogeneous materials，ASME J.Appl.Mech.67（2000）819-822.

［37］J.-H.Kim，G.H.Paulino，Isoparametric graded finite elements for nonhomogeneous isotropic and orthotropic materials，ASME J.Appl.Mech.69（2002）502-514.

［38］K.-J.Bathe，Finite Element Procedures，Prentice-Hall，Englewood Cliffs，1996.

［39］R.D.Cook，D.S.Malkus，M.E.Plesha，et al.，Concepts and Applications of Finite Element Analysis，fourth ed.，John Wiley and Sons，USA，2002.

［40］A.K.Ray，S.K.Das，S.Mondal，etal.，Microstructuralcharacterizationofbamboo，J.Mater.Sci.39（2004）1055-1060.

［41］K.Ghavami，C.S.Rodrigues，S.Paciornik，Bamboo：functionally graded composite material，Asian J.Civil Eng.4（2003）1-10.

［42］S.Askarinejad，N.Rahbar，V.Sabelkin，et al.，Mechanical behavior of a notched oxide/oxide ceramic matrix composite in combustion environment：experiments and simulations，Compos.Struct.127（2015）77-86.

［43］D.Mousanezhad，H.Ebrahimi，B.Haghpanah，et al.，Spiderweb honeycombs，Internat J.Solids Struct.66（2015）218-227.

［44］F.Shalchy，N.Rahbar，Nanostructural characteristics and interfacial properties of polymer fibers in cement matrix，ACS Appl.Mater.Interfaces 7（2015）17278-17286.

［45］H.Salahshoor，N.Rahbar，Nano-scale fracture toughness and behavior of graphene/epoxy interface，J.Appl.Phys.112（2012）023510.

［46］D.Verma，K.Katti，D.Katti，Nature of water in nacre：a 2D Fourier transform infrared spectroscopic study，Spectrochim.Acta A 67（2007）784788. http：//dx.doi.org/10.1016/j.saa.2006.08.033.

［47］B.Mohanty，K.S.Katti，D.R.Katti，et al.，Dynamic nanomechanical response of nacre，J.Mater.Res.21（2006）20452051. http：//dx.doi.org/10.1557/jmr.2006.0247.

［48］Y.Shiji，Y.Muramoto，N.Shimizu，Electrical insulating properties of bamboo and effect of water absorption on them，in：2004 Annual Report Conference on Electrical Insulation and Dielectric Phenomena，2004.CEIDP'04，IEEE，2004，pp.348-351.

［49］D.R.Askeland，P.P.Phul，The Science and Engineering of Materials，Gengage Learning，USA，2003.

20 September 2015

at：Department of Mechanical Engineering，Worcester Polytechnic Institute，Worcester，MA，USA.

E-mail address：nrahbar@wpi.edu（N.Rahbar）.

http：//dx.doi.org/10.1016/j.taml.2015.11.007

2095-0349/©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Biomechanics and Interdiscipline