The critical pressure for driving a red blood cell through a contracting microfluidic channel

Tenghu Wu，Qun Guo，Hongshen M，Jmes J.Feng，c，∗

aDepartment of Chemical and Biological Engineering，University of British Columbia，Vancouver，BC V6T 1Z3，Canada

bDepartment of Mechanical Engineering，University of British Columbia，Vancouver，BC V6T 1Z4，Canada

cDepartment of Mathematics，University of British Columbia，Vancouver，BC V6T 1Z2，Canada

The critical pressure for driving a red blood cell through a contracting microfluidic channel

Tenghu Wua，Quan Guob，Hongshen Mab，James J.Fenga，c，∗

aDepartment of Chemical and Biological Engineering，University of British Columbia，Vancouver，BC V6T 1Z3，Canada

bDepartment of Mechanical Engineering，University of British Columbia，Vancouver，BC V6T 1Z4，Canada

cDepartment of Mathematics，University of British Columbia，Vancouver，BC V6T 1Z2，Canada

A R T I C L EI N F O

Article history：

Accepted 14 November 2015

Available online 28 November 2015

Cell deformation

When a red blood cell（RBC）is driven by a pressure gradient through a microfluidic channel，its passage or blockage provides a measure of the rigidity of the cell.This has also been developed as a means to separate RBCs according to their mechanical properties，which are known to change with pathological conditionssuchasmalariainfection.Inthisstudy，weusenumericalsimulationstoestablishaquantitative connection between the minimum pressure needed to drive an RBC through a contracting microfluidic channel and the rigidity of the cell membrane.This provides the basis for designing such devices and interpreting the experimental data.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：// creativecommons.org/licenses/by-nc-nd/4.0/）.

Red blood cells（RBCs）are extremely flexible.This allows the RBCs to pass through microcapillaries of size much smaller than theirs.When infected by the malaria parasite Plasmodium falciparum，the RBC gradually loses its deformability，which leads to blockage of the blood circulation in microcapillaries.As models for this process，microfluidic assays have been designed in which the critical pressure required to push red cells through a contraction is used as a measure of the cell's deformability［1，2］.Similar devices have been used to separate cells according to their size and rigidity［3］.Since RBCs are known to rigidify under pathological conditions such as malaria infection［4］，microfluidic channels also hold promise as a diagnostic and fractionation tool［5］.Compared with alternative methods to measure mechanical properties of RBCs，such as cell stretching by optical tweezers［6］and micropipette aspiration［7］，the microfluidic channel has the advantage of closely mimicking the flow geometry in vivo.

Ma and coworkers［2，3］have designed a‘microfluidic funnel ratchet，''which consists of a series of contractions followed by sudden expansions（Fig.1）.In such a device，the critical pressure drop for pushing the cell through the channel depends on the deformability of the cell.The more flexible the cell，the less pressure needed.However，no quantitative correlation exists that relates the measured critical pressure drop to the shear and bending moduli of the cell.Ma et al.［2，3］employed the Young-Laplace equation to estimate the cell's cortical tension from the measured critical pressure drop.In this model，the cell was treated as a liquid drop with a constant cortical tension Tc，which was related to the critical pressure dropΔPcthrough where Raand Rbare the radii of curvature at the cell's front and back.However，the cell membrane is elastic and differs considerably from a fluid interface.For example，the in-plane tension will likely vary along the membrane according to the local strain.Besides，the bending rigidity of the membrane may also play a role.

To address these issues，we carry out numerical simulations using a more realistic representation of the mechanical properties of the cell，with an elastic membrane enclosing a viscous cytosol. The physical model and numerical method are based on the recent study of Wu and Feng［8］.The cell membrane is represented by a discrete particle-spring network（Fig.2（a）），with elasticity against in-planestrainandbending（Fig.2（b））.Thefluidsinsideandoutside of the membrane are discretized by particles as well（Fig.2（c）），using the framework of smoothed particle hydrodynamics［9］.Weuse linear springs of an elastic coefficient kssuch that the elastic energy for in-plane deformation is

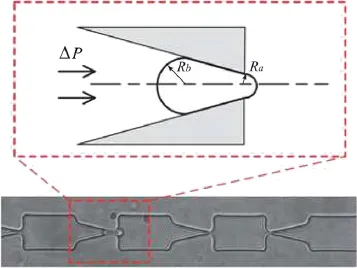
Fig.1.The geometry of the microfluidic device studied by Ma et al.［2，3］. Source：Adapted from Ref.［2］with permission©Royal Society of Chemistry.

where the summation is over all pairs of adjacent vertices i and j，Lijis the length of the spring connecting them，and Lij，0is its resting length.In addition，we adopt the following bending energy［10］：

where kbis the bending modulus and the summation is over all pairs of neighboring triangles i and j andθijis the angle between their normals.Note that this bending energy assumes zero spontaneous curvature for the membrane.

Fig.2.（a）The RBC membrane is modeled by a triangular particle-spring meshwork.（b）Each segment is an elastic spring（Eq.（2）），and there is bending elasticity between neighboring triangles（Eq.（3））.（c）The interior and exterior fluids are discretized by particles，whose movement approximates the Navier-Stokes equation in the smoothedparticle-hydrodynamics framework［9］.

The red cells are known to conserve their surface area.In our particle model，this is implemented through an energy penalty against local area dilatation：

wherekdisaconstantistheundeformedareaofthejthtriangle，and the summation is over all N triangles of the RBC membrane. Finally，we include an energy penalty against the change of the total cell volume：

wherekvisaconstantcoefficient，andV0istheinitialvolumeofthe cell.Under large forcing and severe cell deformation，this volume constraint helps to prevent fluid particles from penetrating the membrane.Using Eqs.（2）-（5），we write the total elastic energy of the cell membrane as Em=Es+Eb+EA+EV.The elastic force acting on each membrane particle can then be calculated as

r being the position of the membrane particle.

The fluid motion is solved by using the smoothed particle hydrodynamics（SPH）method［9］.For the membrane particles，the elastic force fmis added to the hydrodynamic force on the righthandsideofthemomentumequation.Wehavetestedconvergence of the results with respect to spatial resolution.For an initial particle spacing d≤0·15R0，R0being the radius of the undeformed RBC，the numerical results no longer depend on d.Thus，the simulations have been carried out using d=0·15R0.

The surface of the undeformed red cell is obtained from the formula of Evans and Fung［11］：

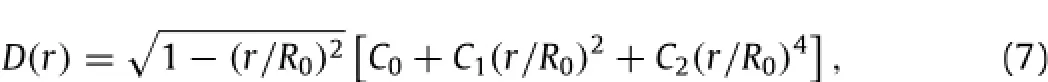
where D（r）is the thickness of the RBC as a function of distance from the center，and R0is the RBC's radius.In our simulation，we set（R0，C0，C1，C2）=（3·9，0·81，7·83，-4·39）µm［12］.With these parameters，the red cell's volume and surface area are about 92µm3and 132µm2，respectively，in agreement with experimental values［13，14］.The triangular mesh on the cell surface was automaticallycreatedbythecommercialsoftwareGAMBIT.Oncethisinitial mesh is created，the edge lengths are taken to be the resting lengthLij，0ofthespringssothattheinitialin-planeenergyisEs=0（cf.Eq.（2））.The shear modulus Gsand bending modulusκof the cell membrane can be related to the coefficients of our mechanical model through［15，16

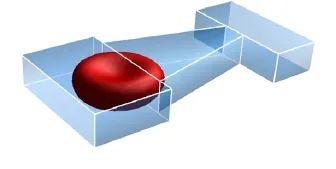
Fig.3.Schematic of the computational domain.

Fig.4.Trajectories of the RBC center of mass through a contraction with T=3µm andw=2·4µm at two pressure drops.

The computational domain is shown in Fig.3.The geometry of the microfluidic channel is inspired by experimental setups of Ma and coworkers［2，3］，as is shown in Fig.1.The entrance has a rectangular cross section of width W and thickness T.The same thickness is maintained throughout the entire conduit，but the width contracts through a 14°slope to a narrower widthw. Further downstream is a sudden expansion to a cross-section that is identical to the one at the entrance.In the simulations，we have kept the segmental lengths constant：l1=7·6µm，l2=12µm，l3=4·4µm，andtestedarangeofT（3-3·6µm）andw（1·8-3µm）values to vary the degree of blockage.Whenwchanges，we vary W according to W=w+9·6µm so that the shoulders upstream and downstream of the contraction maintain constant widths.The shear and bending moduli of the RBC are chosen according to exp-erimental measurements［7，17］：Gs=5 N/µm andκ=2× 1019J.

Figure 4 shows the trajectories of the cell's center of mass xcat two pressure drops.The RBC passes through the contraction at the higherΔP=6 Pa but not the lowerΔP=2·4 Pa.For the lowerΔP，the RBC is eventually stuck in the contraction，with a small tongue extending downstream.Two snapshots of the RBC inside the domain are shown at t=0·02 s and 0.25 s.Note that the model does not account for solid-solid friction between the membrane and the wall.However，a short-range repulsion force is assumed between the membrane and wall particles when their separation falls below a threshold，which is set to be the initial particle spacing d.This repulsion prevents the membrane particles from penetrating the channel walls，but does not affect the result otherwise.TheocclusionisduetotheinabilityoftheRBCtodeform sufficiently，against in-plane and bending elasticity，so as to pass through the narrowest part.For the higher pressure dropΔP= 6 Pa，the red cell does deform sufficiently to pass through the contraction.A snapshot is shown at t=0·24 s that illustrates the passage.We have tested the pressure dropΔP from 1.2 Pa to 6 Pa and determined a critical pressure dropΔPc=4·56 Pa for the geometry of Fig.4.Only pressure drops higher than this can push the RBC through the channel.At lowerΔP，the cell blocks the channel.

Fig.5.The critical pressure dropΔPcrequired to push the RBC through funnel channels depends on the dimensions of the narrowest part of the channel，its thicknessT andwidthw.Experimentaldataoveracomparablerangeofdimensions are also shown for comparison.

In Fig.5，we investigate how the critical pressureΔPcvaries with the dimensions of the narrowest opening，with thickness T and widthw.As expected，the model predicts the critical pressure to decrease with increasingwor T.For the smaller T=3µm，the decreasing trend ofΔPcwith increasingwis stronger，by more than a factor of 4 aswincreases from 1·8µm to 3µm.The trend is milder for the larger T=3·6µm.Besides，we also expectΔPcto rise sharply aswshrinks；this is evident for the T=3µm curve already.

In Fig.5，we have also included experimental data measured in channels with different sizes of the narrowest part，with thickness T ranging from 2·62µm to 3·65µm and widthwfrom 1·7µm to 2·75µm.TheΔPcdata bear out the decreasing trend withw，and generally fall between the two computed curves，although the two T values used in the computation do not bracket the experimental T values perfectly.In light of this，the quantitative agreement may be considered reasonably good.We can speculate on the causes for the discrepancies.For one，we have assumed simple constitutive equations for the membrane elasticity Eqs.（2）and（3）.In reality，theredcellmembraneexhibitscomplexviscoelasticrheology［18］. Furthermore，we have used fixed values for the shear modulus Gsand the bending modulusκ，whereas normal red cells exhibit considerable variability［5，19］.Finally，careful inspection of the experimental data shows that some data points for taller channels（i.e.，larger T）seem to fall above those for channels of smaller T. Thus，experimental errors，e.g.due to solid contact and friction betweenthecellandchannelwall，fluidleakagefortallerchannels，and inaccuracies in measuring the pore dimensions T andw，may have contributed to the discrepancies as well.

Insummary，wehaveemployedadiscreteparticle-basedmodel tosimulatethepassageofRBCthroughafunnel-shapemicrofluidic channel.The simulation results agree well with existing experimental data，and provide a quantitative correlation between the measurable critical pressure dropΔPcand the deformability of the cell.This work suggests the feasibility of using microfluidic essaysfor measuring cell deformation and separating cells according to their rigidity，potentially providing a diagnostic for diseases such as malaria.For this purpose，of course，larger-scale computations need to be carried out to build a database covering wider ranges of geometric parameters as well as mechanical parameters that correspond to healthy and diseased cells.

Acknowledgments

The study was supported by the Natural Sciences and Engineering Research Council of Canada（NSERC）and the Canada Research Chair program.JJF acknowledges additional support by the Peter Wall Institute for Advanced Studies during his tenure as Wall Scholar.TW acknowledges partial support by the Chinese Government Award for Outstanding Self-Financed Students Abroad.HM acknowledges funding from the Canadian Institutes of Health Research and the Canadian Blood Services.QG acknowledges funding from the UBC Four Year Doctoral Fellowship.

［1］J.P.Shelby，J.White，K.Ganesan，et al.，A microfluidic model for single-cell capillary obstruction by Plasmodium falciparum-infected erythrocytes，Proc. Natl.Acad.Sci.USA 100（2003）14618-14622.

［2］Q.Guo，S.J.Reiling，P.Rohrbach，et al.，Microfluidic biomechanical assay for red blood cells parasitized by Plasmodium falciparum，Lab Chip 12（2012）1143-1150.

［3］S.M.McFaul，B.K.Lin，H.Ma，Cell separation based on size and deformability using microfluidic funnel ratchets，Lab Chip 12（2012）2369-2376.

［4］C.A.Moxon，G.E.Grau，A.G.Craig，Malaria：modification of the red blood cell and consequences in the human host，Br.J.Haematol.154（2011）670-679.

［5］Q.Guo，S.P.Duffy，K.Matthews，et al.，Microfluidic analysis of red blood cell deformability，J.Biomech.47（2014）1767-1776.

［6］M.Dao，C.T.Lim，S.Suresh，Mechanics of the human red blood cell deformed by optical tweezers，J.Mech.Phys.Solids 51（2003）2259-2280.

［7］G.B.Nash，E.O'Brien，E.C.Gordon-Smith，etal.，Abnormalitiesinthemechanical propertiesofredbloodcellscausedbyPlasmodiumfalciparum，Blood74（1989）855-861.

［8］T.Wu，J.J.Feng，Simulation of malaria-infected red blood cells in microfluidic channels：Passage and blockage，Biomicrofluidics 7（2013）044115.

［9］J.J.Monaghan，Smoothed particle hydrodynamics，Rep.Progr.Phys.68（2005）1703-1759.

［10］S.Wada，R.Kobayashi，Numerical simulation of various shape changes of a swollen red blood cell by decrease of its volume，Trans.Japan Soc.Mech.Eng. 69（2003）14-21.

［11］E.Evans，Y.Fung，Improved measurements of the erythrocyte geometry，Microvasc.Res.4（1972）335-347.

［12］S.M.Hosseini，J.J.Feng，Aparticle-basedmodelforthetransportoferythrocytes in capillaries，Chem.Eng.Sci.64（2009）4488-4497.

［13］A.Esposito，J.Choimet，J.Skepper，et al.，Quantitative imaging of human red blood cells infected with Plasmodium falciparum，Biophys.J.99（2010）953-960.

［14］Y.M.Serebrennikova，J.Patel，W.K.Milhous，et al.，Quantitative analysis of morphological alterations in Plasmodium falciparum infected red blood cells through theoretical interpretation of spectral measurements，J.Theoret.Biol.265（2010）493-500.

［15］T.Omori，T.Ishikawa，D.Barthes-Biesel，et al.，Comparison between spring network models and continuum constitutive laws：Application to the large deformation of a capsule in shear flow，Phys.Rev.E 83（2011）041918.

［16］D.H.Boal，M.Rao，Topologychangesinfluidmembranes，Phys.Rev.A46（1992）3037-3045.

［17］E.Evans，New membrane concept applied to the analysis of fluid shear-and micropipette-deformed red blood cells，Biophys.J.13（1973）941-954.

［18］D.A.Fedosov，B.Caswell，G.E.Karniadakis，A multiscale red blood cell model with accurate mechanics，rheology，and dynamics，Biophys.J.98（2010）2215-2225.

［19］R.M.Hochmuth，R.E.Waugh，Erythrocyte membrane elasticity and viscosity，Annu.Rev.Physiol.49（1987）209-219.

5 September 2015

at：Department of Chemical and Biological Engineering，University of British Columbia，Vancouver，BC V6T 1Z3，Canada.

E-mail address：jfeng@chbe.ubc.ca（J.J.Feng）.

http：//dx.doi.org/10.1016/j.taml.2015.11.006

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http：//creativecommons.org/licenses/by-nc-nd/4.0/）.

Erythrocyte deformability Membrane modulus

Membrane rigidification Capillary occlusion

*This article belongs to the Biomechanics and Interdiscipline