星载周扫式跟踪转台运动轴与光轴关系的建模分析

杨恭勇， 张立中

（长春理工大学，长春130022）

0 引言

卫星激光通信技术是以激光作为信息载体进行星间、星地之间建立的高速、大容量的数据传输技术，具有广阔的应用前景［1］。卫星间的通信方式主要是以微波通信和激光通信为主。由于微波波长较长，要求微波天线较大，会造成通信终端的体积和质量大、功率消耗高等缺点，随着现代通信网络对通信容量的需求不断提高，微波又逐渐暴露出自身容量不足的缺点，越来越不能满足现代通信网络的要求。与微波相比，激光具有的传输信息量大，传输速率高，方向性好，隐蔽性好，抗干扰能力强等优点，使得激光通信成为实现大数据高速率保密传输信息的最优方式之一［2］。

星载周扫式跟踪转台具有重量轻、转动负载小、转动范围大、不存在像旋等优点，常用于小口径轻小型卫星终端系统中［3］。终端系统中转台的结构形式与反射镜的安装方式决定了光线的传递方式，而在扫描和跟踪的过程中，机构中反射镜的坐标系相对于基准坐标系是不断变化的，这使得光通信终端的光学传递关系也随之不断变化，因此确定终端系统的运动轴与光轴的关系是结构设计首要任务。本文利用向量旋转与坐标变换理论推导出终端系统的运动轴与光轴的关系，对相似的光学系统的光路运动问题提供了一定的借鉴。

1 跟踪转台的结构及工作原理

卫星间的光通信为实现大范围的扫描，转台通过方位、俯仰轴系的配合进行圆周扫描，跟踪转台具体的结构组成如图1所示。

图1 机械结构总体设计示意图

周扫式跟踪转台主要由通过万向节连接的方位和俯仰两套轴系组成，两套轴系结构相似，以相互垂直的方式安装，都是由电机直驱，通过旋转变压器确定旋转角度位置，两个正交轴上的反射镜呈45°安装在万向节上。入射光束透过保护镜经过两面反射镜的反射进入终端的光学系统，通过透镜聚焦在CCD成像系统上，形成光斑，经过对光斑信息的数字化处理后计算出系统运动轴与光束指向角度的偏差，通过控制方位与俯仰两轴运动，使两面反射镜到达指定的位置，修正光斑位置的偏差，保持CCD上呈现的光斑处在其坐标系的中心位置，从而实现自动跟踪。这就需要将转台两轴的运动变量与光路的传播角度关联起来，即数学模型的建立与数学关系的推导过程。

2 跟踪转台的数学建模分析

在计算系统中运动轴与光轴传递矩阵之前，需要对相关的坐标系进行建立。

2.1 坐标系的建立及基本公式

建立三维直角坐标：1）光学系统坐标系oxyz。o为光轴中心，以垂直轴向上为z轴的正向，以水平轴指向第一面反射镜为y轴的正向，垂直yz方向为x轴，z为光学系统主轴，x、y轴与CCD相机靶面坐标平行。2）方位轴坐标系o1x1y1z1。o1为反射镜1中心，z1为方位轴的主轴，与z同轴，坐标系oxyz的x、y轴绕z1轴逆时针旋转α角得到x1、y1轴。3）俯仰轴坐标系o2x2y2z2。o2为反射镜2中心，y2为俯仰轴的主轴，与方位轴坐标系o1x1y1z1中y1同轴，坐标系o1x1y1z1的x1、y1轴绕y2轴逆时针旋转β角得到x2、z2轴。

图2 系统指向时入射光的坐标系关系

任意矢量绕坐标轴正向旋转某一角度的变换矩阵［4］分别为：

当入射光通过反射镜后，则

其中：A0为入射光线矢量；A1为出射光线矢量；R为反射作用矩

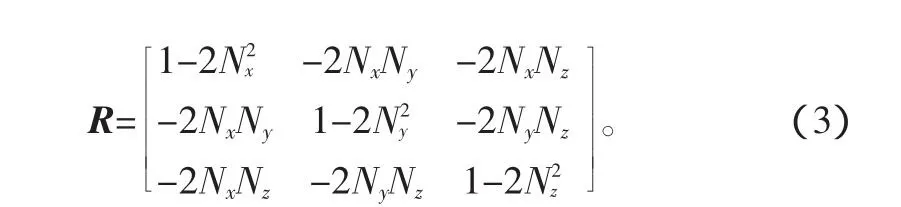
其中，Nx、Ny、Nz为平面反射镜法线矢量n的方向余弦：

3.2 指向过程中运动轴与光轴关系分析

1）反射镜1随坐标系o1x1y1z1绕z1轴转过α角后，反射矩阵为

2）反射镜2随着坐标系o1x1y1z1绕z1轴转过α角后，又随坐标系o2x2y2z2绕y2轴转过β角后，反射矩阵为：

理想状态下，入射光线矢量为Ain，到达CCD相机上的光线矢量正中靶心，光线矢量为A0=［0 0 －1］T，若此时转台的方位、俯仰轴系分别转动了方位角α、俯仰角β，根据反射定理A0=R1R2Ain，则可推导出系统可接受到的入射光矢量为

若得知在oxyz坐标系下空间任意光线 Ai，其与z轴夹角为θ，在 oxyz面内投影与y轴夹角为φ，此时，Ai=，令Ai=Ain，可得到：

图3 空间任意入射光线的空间位置

图4 系统跟踪时入射光的坐标系关系

此时将转台的方位轴角度调整到α=π/2-θ，俯仰轴角度调整到β=θ，入射光线落到CCD平面中心，完成指向功能。

3.3 跟踪过程中光轴与运动轴关系分析

当跟踪转台转动方位轴到α，俯仰轴到β时，任意入射光Ain经过两面反射镜反射后到达CCD相机上的光线矢量为［x1y1z1］T，矢量单位化［5］后为

为了实现跟踪效果，跟踪转台的方位、俯仰轴分别转动Δα、Δβ，进行微量调整，此时，光线到达CCD相机上靶心位置，光线矢量为 A=［Δx Δy Δz］，完成跟踪。当到达 CCD相机上的光线矢量为 A=［Δx Δy Δz］T时，CCD 接收平面上的脱靶量分别为Δx、Δy，根据反射定理，此时入射光线矢量

其中

跟踪转台的方位、俯仰轴分别转动Δα、Δβ，调整姿态后，Δx=此时：

1）反射镜1随坐标系o1x1y1z1绕z1轴转过α角后，反射矩阵为

2）反射镜2随着坐标系o1x1y1z1绕z1轴转过α角后，又随坐标系o2x2y2z2绕y2轴转过β角，反射矩阵为

转台调整姿态前后，同一束入射光经过两面反射镜反射，到达CCD接收平面不同位置，可得到关系式

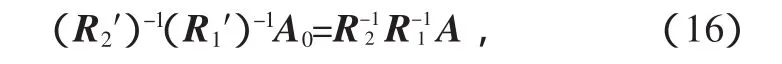
即

由此可得

图 5 Δβ 与Δx，Δy的关系

图6 Δα与Δx，Δy的关系

在跟踪过程中CCD平面接受光线A→0，即Δβ→0，Δα→0，可近似认为sinΔ=Δ，可求得 Δα、Δβ与脱靶量Δx、Δy的近似关系：

4 结论

在卫星激光通信中，快速确定信标光位置并稳定进行跟踪是实现高速激光通信的重要前提保障。

在地面演示实验中，已知目标信号光的情况下，根据公式（8）可以迅速变换跟踪转台的姿态，实现对信标光的指向。目标在移动过程中，根据公式（20）、公式（21）可迅速对跟踪转台的运动轴进行微调整，实现对目标的实时跟踪。

［1］ Chan V W S.Optical space communications［J］.IEEE J.Quantum Electron，2002（6）：959-974.

［2］ 侯睿，赵尚弘，胥杰，等．空间环境对卫星光通信系统性能的影响分析［J］.光学技术，2008（34）：223-226.

［3］ 谭立英，吴世臣.潜望镜式卫星光通信终端的CCD粗跟踪［J］.光学精密工程，2012，20（2）:271-276.

［4］ Gatenby P.Small laser terminal for operational intersatellite links Space Communition［C］//SPIE Proc，1996，699：71-80.

［5］ 刘素美，马红章.45°镜多元并扫成像特性及扫描轨迹研究［J］.红外，2007，28（3）:9-13.