用人体平面刚体模型分析太极拳在水平、垂直、横向力作用下的力学原理

顾 杰，郭振兴，马秀杰

（邯郸学院 太极文化学院，河北 邯郸 056005）

太极文化研究

用人体平面刚体模型分析太极拳在水平、垂直、横向力作用下的力学原理

顾 杰，郭振兴，马秀杰

（邯郸学院 太极文化学院，河北 邯郸 056005）

在对《用人体平面刚体模型分析太极拳在水平作用力下的力学原理》研究的基础上，进一步分析了太极拳在三维作用力下的力学原理，推导出更接近实际和具有普遍意义的稳定和失衡临界（失根和打滑）定量分析三大公式，给定了规范太极拳动作和技术的力学方法。以特例、算例、实例等不同形式具体计算和分析了弓步、坐步、分脚、弓步掤、坐步捋等太极拳基本技术动作的受力状况和失衡临界点，阐述了三大公式在不同情形下的运用方法，太极拳基本动作的力学原理和力学规范。甲乙双方推手，比的是功架的力学性能。“甲方坐步捋胜乙方弓步掤”是太极拳的经典结论。通过用三大公式对该结论作定量分析。数据表明轻者甲方可用“四两”将乙方的“千斤”“拨”离平衡，重者甲方可将乙方发出一丈之外。三大公式为王宗岳的“耄耋能御众”找到了现代力学的基础。推手比的是技术，比的是如何运用合适的功架。 三大公式为推手分析提供了定量工具。

太极拳；力学分析；人体平面刚体模型

引言

太极拳是一种具有健身和搏击功能的肢体运动，无论是自我练习还是与人对抗都是依靠身体的位移和肢体的动作变换。因此，太极拳“掤、捋、挤、按、采、挒、肘、靠”等技术的运用都必然依靠人体质量、速度和力学构造的共同作用。人体质量和速度的乘积在力学中称为人体动量，人体动量是太极拳运动的重要因素［1］54-69。太极拳推手就是一方的动量作用于另一方动量，两方的动量相互作用发生碰撞，在身体的接触点产生力。从力学意义上讲就是碰撞产生力［2］82-107。

太极推手碰撞产生的力是一对力：作用力和反作用力。作用力作用于乙方；反作用力作用于甲方；作用力和反作用力大小相等方向相反。力是一个矢量， 通常有三个分量。文献［2］仅仅讨论了水平分量的效果。本文将讨论三个分量同时作用的力学效果。太极拳中力的方向分法众多，有水平、垂直、横向、侧上、侧下、向后等，例如“揽雀尾”中的“捋”就是向后、横、侧下方拖动乙方，本文按照力学分法将其简约为水平、垂直、横向三个方向。最大攻击力的取决于功架的形式和发力的方式。实际能发出的力小于或等于最大攻击力，这时甲方在临界条件内，而保持稳定。太极拳中的力分为传递力（由脚底传递到全身的力）、整体动量力（人体整体动量的碰撞力）、相对动量力（肢体相对运动动量的碰撞力）三种。三种力常是联合使用，也能够单独使用。

历代太极拳大家从不同侧面论述过上述观点，武式太极拳宗师武禹襄在《太极拳论》中讲：“……其根在脚，发于腿，主宰于腰，形于手指。由脚而腿而腰，总须完整一气……”；杨式太极拳宗师杨澄甫在《太极拳说十要》中强调：“上下相随者，即太极拳论中所云：“其根在脚……” ；都强调了力源于脚底和大地的密切联系，下肢稳住了，上肢或身体其他部位才能实现攻防的意向；还言明了力的传递过程。太极拳宗师王宗岳在《十三势行功心解》中说：“……所谓变动虚实也，……运劲如百炼钢，……发劲如放箭，……蓄而后发，……”“……曲中求直，蓄而后发。力由脊发，……” 这众多文字细述了人体整体动量和肢体相对动量这两种力的形成与功能，强调有效攻击的形成要依靠躯体与上肢的配合，腰脊是反冲基地，手臂是攻击器，两者依靠身体的曲伸产生相对运动，腰脊部位的大质量低速度动量造成手或手臂的快速打击力。太极拳中的“长劲”主要是指用传递力和整体动量的发劲方法，“短劲”主要是指用相对动量的发劲方法［3］10-17。

文献［1］、［3］主要讨论了太极拳的力学原理，文献［2］提出了人体平面刚体模型的概念，并通过对太极拳水平方向作用力（水平力）的研究，得出了太极拳力学研究的基础数学模式。本文在文献［2］的基础上，进一步完善了人体平面刚体模型的力学条件，在传递力、整体动量、相对动量三大力源中纳入了人体角动量的影响；将发力方向增加为水平、垂直、横向三个方向；并以太极推手技法“弓步掤”、“坐步捋”为例，分析了太极拳基本动作的力学原理，推导出相关研究可用的数学模式和运算软件。

一、水平、垂直、横向作用力下的人体平面刚体模型

有水平、垂直、横向力作用于人体的平面刚体模型。这里把人体简化为平面内的一个刚体模型，各肢体简化成刚杆，刚杆的接点为刚性；脚和地面的接触处简化为点；刚体的质心和重心重合；并根据研究需要设定了若干力学条件，见图1。图1形似弓步，但对其他步型都适用。例如，前脚距离小于后脚距离时可认为是弓步；前脚距离大于后脚距离时可认为是坐步；前脚距离大大于后脚距离时可认为是虚步。只要选择合适的参数，图1的模型适用于任何步型。

图1　平面刚体模

图中：

m=60（ kg）--人体质量

W=mg--人体重力垂直向下，作用于重心

g=9.8m/s2--重力加速度

mj=2（ kg）--手的质量

Fx--乙方对甲方施加的水平外力，向左为正

Fy--乙方对甲方施加的垂直外力，向下为正

Fz--乙方对甲方施加的横向外力，进纸为正

Nq--地面对前脚的正向支撑力

Nh--地面对后脚的正向支撑力

fqx--地面对前脚的水平摩擦力，向右为正

fhx--地面对后脚的水平摩擦力，向右为正

fqz--地面对前脚的横向摩擦力，出纸为正

fhz--地面对后脚的横向摩擦力，出纸为正

Lq--重心到前脚的水平距离

Lh--重心到后脚的水平距离

Ls--接触（手）处到重心的水平距离

Hz--重心到地面的高度

Hj--接触（手）处到地面的高度

v0x--人体质心处的水平初速度，向右为正

v0y--人体质心处的垂直初速度，向上为正

v0z--人体质心处的横向初速度，出纸为正

L0x--质心水平匀减速运动距离

L0y--质心垂直匀减速运动距离

L0z--质心横向匀减速运动距离

Ljx--手水平匀减速运动距离

ωy--人体绕Y轴的垂直初角速度，左旋为正

tanθ=μ=0.5-摩擦角正切等于摩擦系数

φxy-XY 平面内平动的力线角

φq-前脚总力线角

φh-后脚总力线角

圆柱转动惯量：

二、人体动力学分析

太极拳的基本要求是保持甲方稳定，迫使乙方失衡。失衡的标志是在外力作用下脚底打滑（简称打滑）或脚底失去正压力（简称失根）。

按照图1所示，将人体简化为平面刚体模型采用隔离体分析法，运用动力学平衡原理分析和推导人体在水平力、垂直力、横向力共同作用下的受力状况、稳定条件和打滑、失根条件，以及相互关系和数学计算模式。

图1中重力线与地面的交点是O，取定轴为通过O点垂直于纸面的直线。水平力和力的高度Hj形成逆时针力矩；垂直力和力臂Ls形成顺时针力矩；前脚支撑力Nq和前脚距离Lq形成逆时针力矩；后脚支撑力Nh和后脚距离Lh形成顺时针力矩。加速度apx向左，角加速度逆时针；加速度apy对过O点的臂为零，没有角加速度；人体的转动惯量是将这些条件代入转动定律我们得到：

解方程组（2）（3），并写入保根条件（地面对脚的正向支撑力大于或等于零），得：

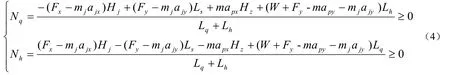
将摩擦力按正压力分配，并限以不打滑条件（力线角的正切小于或等于摩擦系数），得：

由（1）式可知，摩擦力之和为：

由（2）式可知，正压力之和为：

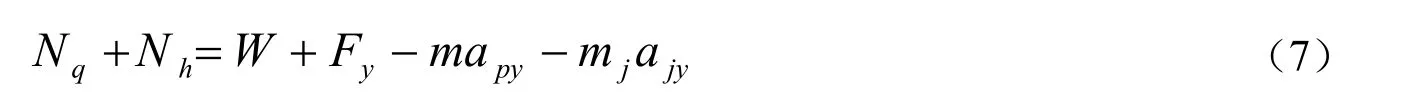
因力线角的正切等于摩擦力之和与正压力之和之比，所以（6）式除以（7）式得：

在横方向（Z）由牛顿第二定律，得：

将转动定律运用于质心Y轴，得：

解方程组（9）（10），并写入不打滑条件，得：

（11）写入的不打滑条件中两脚正压力由（4）式给出，没打滑前两脚横向摩擦力与正压力之比是YZ平面内的力线角，即：

将（4）（11）代入（12），并写入不打滑条件，得：

各脚的总摩擦力为：

各脚的总的力线角应小于摩擦角，即：

综合上述推算与分析，得出人体在水平力、垂直力、横向力共同作用下保持稳定的必要条件以及计量方法（稳定公式）：

由文献［2］知，人体失去地面的支持的临界条件是地面对脚的正向支撑力为零，也即失根临界条件，其计算公式（失根公式）是：

由文献［2］知脚底打滑的临界条件是力线角的正切等于摩擦系数，即打滑临界条件，其计算公式（打滑公式）：

上述（16）、（17）、（18）三个公式是太极拳力学分析的基本公式，具有普遍应用意义。不仅能分析单一方向作用力，而且能分析多方向作用力；不仅能分析单一力源的作用，而且能分析多种力源的作用。因而，能分析太极拳的基本动作、基本技术和各种复杂发力，能量化脚底打滑、失根的临界条件，能计算推手时双方的接触力、失衡临界点和各方的平衡度。

太极拳的力，尤其是推手中双方的相互作用力有大小和方向，是个三维力。力的方向在传统太极理论中分为“四正四隅”，意为四面八方。在近代力学中力的方向更精确的表示为三个方向，或称力有三个分量。调节三个分量的量值和符号可得到任何方向的力。本文将力表示于水平、垂直和横向三个坐标轴组成的坐标系中，因此力有水平、垂直和横向三个分量。

最大发力量取决于力的来源及其分配。文献［2］的结论是太极拳的力源分为传递力（由脚跟传递来的力）、整体动量（人体整体动量的碰撞力）、相对动量（肢体相对运动动量的碰撞力）三种。这个结论对本文的三维力分析完全适用。实际发力量小于或等于最大发力量。否侧甲方将越过临界条件，最终导致失稳。

在太极推手中，力源和力的方向有多种组合，各种组合合成为具有不同功能和不同威力的作用力。方向用“维度”表示，力源用“源”表示。例如：一个方向和一种力源称为一维一源力，或按方向称为水平力、垂直力、横向力；两个方向和两种力源称为二维二源力；三个方向和三种力源称为三维三源力。

二、一维水平力三源的特例

只有水平力和速度时稳定公式（16）式简化为文献［2］中的（23）式；失根公式（17）简化为文献［2］中的（21）式；打滑公式（18）为文献［2］中的（24）式。因而本文的结论和文献［2］的完全一致。本特例中，攻击力在水平方向；力源可来自于传递力、整体动量碰撞力和相对动量碰撞力。

三、一维垂直力三源的特例

只有垂直力和速度时（水平、横向的力和速度为零）稳定公式（16）式简化为：

摩擦力等于零，所以没有打滑临界点，即永远不会打滑。

失根临界条件可令（19）中第4或5式为零而得。

本特例中，攻击力在垂直方向；力源可来自于传递力、整体动量碰撞力和相对动量碰撞力。

我们来看一个一维（垂直）一源（传递力）弓步的特例计算，垂直力没有速度时弓步输入数据为：

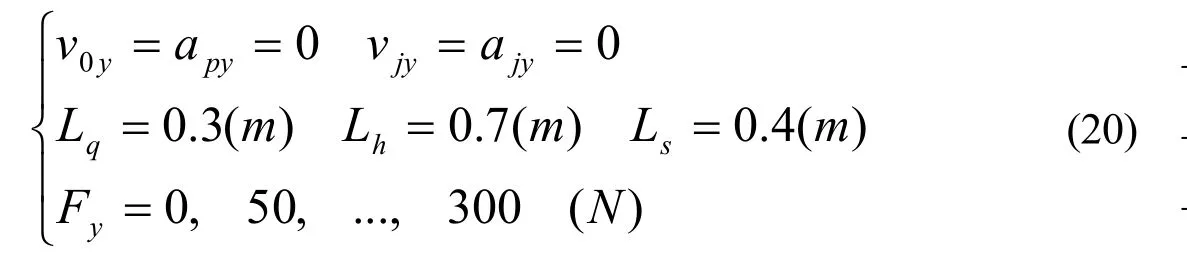
将（20）代入（19）计算结果如表1。

表1　垂直力下弓步的正压力和摩擦力

由表一可见，弓步在只承受垂直力时，前脚的正压力随外力递增而增加，没有理论上的限制。实际的限制来自人体构架的保型能力。后脚的正压力随外力递增而减小，但减小幅度很小。

打滑临界力：因为只有垂直力，所以摩擦力等于零，也就没有打滑条件，即弓步仅在垂直力作用下不会打滑。

失根临界力：弓步的失根临界条件是后脚正压力为零，即公式（19）中第5式为零。如令（19）中第5式为零，可算得致使弓步失根的临界力牛顿。这个力的数值比较大，所以弓步仅在垂直力下，一般不会失根。

上述的计算和分析都是假设弓步与乙方接触的手探出前脚10厘米如果手不探出前脚，则弓步更不会失根。因此，在只有垂直力作用的情况下，与乙方接触的手越靠近身躯越有利于全身稳定。如果计入质心速度和手速度（一维三源垂直方向），仍可得出类似的结果。详细分析此处从略。

四、二维水平和垂直组合力三源的特例

当图1所示模型受到水平力和垂直力合成的二维力作用并有速度时，稳定公式（16）简化为：

打滑临界条件公式：令（21）式第6式等于摩擦系数得出。失根临界条件公式：令（21）式第4或5式为零得出。

为方便解题，令垂直力和水平力成正比，即：

将（22）代入临界条件可解出临界力Fx。

我们来看一个二维（水平和垂直组合力）一源（传递力）弓步的特例计算，水平和垂直组合力没有速度时弓步输入为：

将（23）代入（21）计算出正压力和摩擦力如表2。由表2可见，打滑先于失根。

打滑临界力：根据打滑条件，令（21）式第6式等于摩擦系数，算得打滑临界力牛顿。当力线角增至摩擦角后（tanφ≥μ），水平力将大于摩擦力。摩擦力等于正压力和摩擦系数的乘积。公式（21）变为：

表2　水平和垂直组合力下弓步的正压力和摩擦力

公式（24）中第1式表明，水平力大于摩擦力的部分将加速人体打滑，人体将最终滑出赛场。表二中自牛顿以下各行（至下一个临界条件）的数值是由（24）式计算。

失根临界力：根据失根条件，令（21）式第4式等于零，算得出失根力牛顿。当前脚正压力递减至零时，后脚正压力递增至承受全部正压力并保持不变。其后外力矩大于重力矩，前脚正压力为零并保持不变，后脚承受全部重力、垂直外力，和全部摩擦力的最大值。（21）式变为，

公式（25）中第1式表明，水平力和垂直力对后脚的力矩大于重力对后脚的力矩。两个力矩的差值将加速人体而最终被掀翻。表二中自以下各行数值由公式（25）式计算。

前脚摩擦力增至峰值后递减，当该脚正压力为零后摩擦力也为零。后脚摩擦力递增至承受全部摩擦力。全部摩擦力等于重力与垂直力之和乘以摩擦系数。

文献［2］表一给出仅有水平力作用下人体平面模型的分析，比较文献［2］表一和本文表二可见垂直力的加入使临界值增加。表三是无有垂直力时临界力的比较。由表三可见，水平和垂直组合力使人脚底打滑、前脚失根的力大于单一水平力。

表3　仅有水平力作用下和水平垂直组合力作用下临界力的比较

由此可见攻击时斜向上能增加进攻能力。杨式太极拳“揽雀尾”的“掤势”和“按势”就是具体运用。

五、一维横向力三源的特例

当图1所示模型受到横向力作用时并有速度时，稳定公式（16）简化为：

失根临界力：因为只有横向力，所以重心能够一直保持在两脚间，也就永远不会失根。

打滑临界力：打滑临界条件：令（26）式第10或11式等于摩擦系数。

我们来看一个一维（横向力）一源（传递力）弓步的特例计算，只有横向力没有速度时的弓步输入为

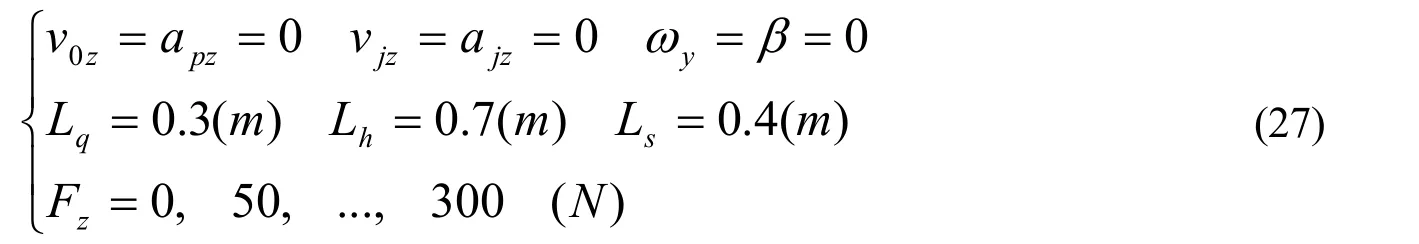
将公式（27）代入公式（26）计算出横向力作用下弓步的正压力和摩擦力如表4。

由表4可见，在只承受横向力时，弓步前后两脚的正压力是身体重力之和，不随外力变化而变化。两脚摩擦力的计算和正压力没有关系；后脚的摩擦力呈现负值，是因为摩擦力的方向进入纸面方向（图1中的摩擦力出纸为正，入纸为负）。

表4　横向力下弓步的正压力和摩擦力

式中ad是人体质心的加速度，是人体的角加速度。人体绕后脚加速，因而有，

将（29）代入（28），得：

解（30）得：

后脚的摩擦角为：

因外力分配于前脚的力是Fqz，所以，

将（31）代入（33），计算出前脚的力，

前脚的摩擦角为，

用（28）（31）（32）（35）取代（26）中的相应公式，得前脚打滑后的公式得出前脚打滑后保持稳定的必要条件以及计量方法，即稳定公式（16）在简化为公式（26）后，进一步简化为专用公式：

本例可用来模拟杨式太极拳的“野马分鬃”、“斜飞式”等横向攻击动作。下盘弓步，前手横向挒乙方。甲方的最大攻击力是牛顿。甲方攻击乙方的横向。文献［2］中算出乙方最多能承受64.1牛顿。可见甲方击倒乙方是绰绰有余。

具有质心速度、手速度和人体角速度的计算给出类似的结果。质心速度、手速度和人体角速度大大的增加了甲方的攻击力。这里从略。

六、甲方三维（水平、垂直和横向力）一源（传递力）的坐步和乙方三维一源弓步的推手

甲方和乙方接触，接触处的力有大小方向。一般情况下力有三个方向的分量。比如杨式太极拳揽雀尾的捋，甲方向后、横、下方向拖带乙方。捋时常用坐步。图1的模型也适用于坐步。坐步前脚距离大，后脚距离小，只需带入合适的参数。稳定公式（16）包括在接触处三种力源的效果：由脚根传递来的力、人体整体的动量的碰撞力、肢体相对运动动量的碰撞力。打滑临界条件由（18）给出。失根临界条件由（17）给出。哪个临界条件先满足最好由列表计算的趋势而定。

在太极推手中有传递力、整体动量、相对动量等三种力源的应用（发力），有时单用一种，有时两种合用，更多是三种合用。先分析只有传递力的情况。

假设乙方下盘为弓步，上盘以掤势向甲方进攻，见图3。甲方下盘坐步，上盘以捋势发劲，见图2。

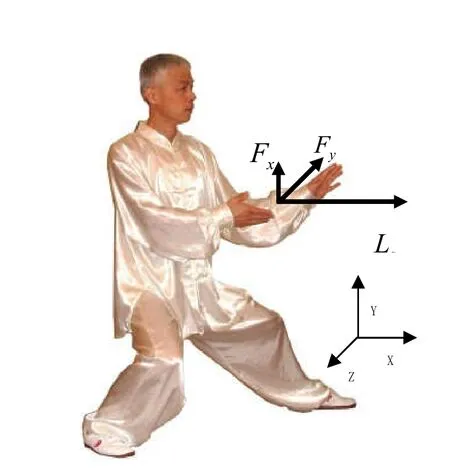
图2　甲方坐步捋势

图3　乙方弓步掤势

图4　乙方弓步侧向

先分析甲方。三维力时坐步的输入是，

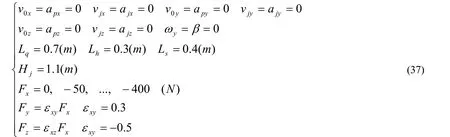
乙方作用于甲方的水平力是拉力，根据图1的符号规则Fx取一系列负值。类似的，垂直力Fy为负值，横向力Fz为正值。垂直力和横向力按由比例输入。将数据（37）式代入稳定公式（16）计算出正压力和摩擦力如表5。

由表5可见，甲方后脚打滑先于前脚打滑和后脚失根。由打滑公式（18）的第2式算出，当牛顿时后脚开始打滑，这也是坐步能有的最大纵向拉力。由数据（37）中第6、7式可算知，当牛顿时，相应的垂直力牛顿，相应的横向力牛顿。

表5　三维力下坐步的正压力和摩擦力

再分析乙方。注意乙方的坐标系绕Y轴旋转了180度（见图3和图4）， 这样图1的模型仍然适用于乙方。图3中纵向弓步的输入是，

将数据（38）代入公式（16）可算出乙方弓步的力学效果，算表从略。

甲方坐步纵向最大拉力226牛顿大于乙方弓步纵向抵抗拉力141.9牛顿，所以甲方能使乙方后脚打滑。这里以水平力为基数，垂直力及横向力都与水平力成比例。

设想甲方捋乙方弓步的侧向。乙方侧向面对甲方，见图4。乙方弓步侧向的输入是，

将（39）代入（16）可算出乙方侧向弓步的力学效果，算表从略。

甲方坐步纵向最大拉力226牛顿远大于乙方弓步侧向抵抗拉力58.6牛顿，所以甲方能使乙方后脚打滑。

特别要注意的是这里比较的是功架的力学功能。这跟体能是不同的概念。强壮的人用了不合适的功架也会失败。而耄耋老者运用合适的功架却能打败强壮的对手。

按照牛顿第三定律，两方接触，产生一对作用力与反作用力。称甲方作用于乙方的力为作用力，则乙方作用于甲方的力为反作用力。根据牛顿第三定律作用力和反作用力大小相等方向相反。乙方在水平方向作掤势。甲方在三个方向发力。尽管乙方试图攻于水平向，由于甲方加攻垂直向和横向，两方间的作用力和反作用力仍然具有三个方向，并且量值相等，见表 6。作用于甲方的水平力向左，作用于乙方的水平力向右；作用于甲方的垂直力向上，作用于乙方的垂直力向下；作用于甲方的横向力向内，作用于乙方的横向力向外。注意在表中各力的取值随着模型的坐标系而定。乙方的坐标系绕Y轴旋转了180度。因而根据图1中的符号规则：甲方的水平力在甲方坐标系中取负值，乙方水平力在乙方坐标系中取负值；甲方垂直力在甲方坐标系中取负值，乙方垂直力在乙方坐标系中取正值；甲方横向力在甲方坐标系中取正值，对横向力在乙方坐标系中取正值。

表6　作用三维力和反作用三维力

甲方可发水平力的最大值是226牛顿（表6第3行）。在此范围内甲方平衡，既不失根，也不打滑。当甲方的水平力是58.5牛顿时，导致以方侧向弓步临界打滑，其后失效。类似地，当甲方的水平力是141.9牛顿时，导致方纵向弓步临界打滑，其后失效。所以226牛顿是储备，并不是甲方需要发的力。只要甲方临界力大于乙方临界力，就能打败乙方。而打败乙方时，甲方只需发和乙方临界力等量的力。

总之，通过力学分析，表明“坐步捋”是应对“弓步掤”有效方法，同时证明了太极拳“牵动四两拨千斤”理论的可靠和战术的巧妙。

上述分析，虽然接近实际，具有说服力，但由于平面模型的局限，忽略了人体的侧向尺度，要弥补这一缺憾，还需在后续研究中建立人体立体刚体模型。

七、甲方三维（水平、垂直和横向力）二源（传递力和整体动量碰撞力）的坐步特例

在前例坐步的基础上，本例在力源中增设了整体动量以分析甲方在三维二源情况下的力学效应，见图 5。坐步纳入整体动量的输入是，

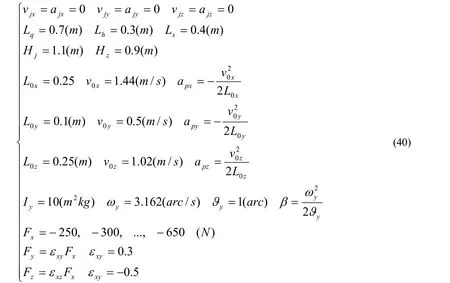
将数据（40）代入稳定公式（16）计算坐步的正压力和摩擦力如表7。

图5　甲方坐步整体动量捋势

表7　纳入整体动量后坐步的正压力和摩擦力

由表可见，后脚打滑将先于前脚打滑和后脚失根。由（18）第2式算出牛顿时后脚开始打滑。该力远大于没有整体动量时的最大攻击力（226牛顿）。所以人体的总动量增加捋的功能。相应的垂直力是牛顿，相应的横向力是牛顿。

八、甲方三维三源坐步捋和乙方三维二源（没有相对动量）弓步掤推手

三维三源是一般情况，在太极拳套路中处处可见，在太极推手中使用的最普遍。三维三源情况下有稳定公式（16）、失根公式（17）和打滑公式（18）。三维三源坐步的输入是，

图6示出了甲方三维三源时的示意图。

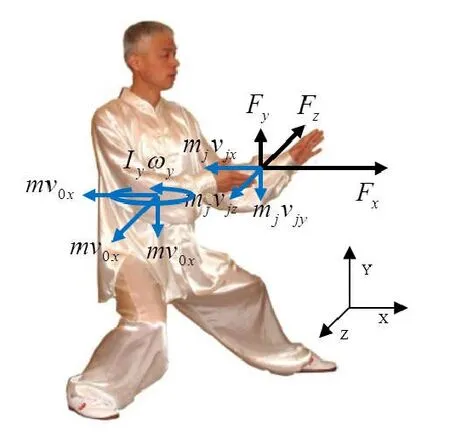
图6　甲方三维三源坐步捋势

将数据（41）代入稳定公式（16）计算出坐步的正压力和摩擦力如表8。

表8　纳入整体和相对动量后坐步的正压力和摩擦力

由表8可见，后脚打滑将先于前脚打滑和后脚失根。由打滑公式（18）中第2式展开，

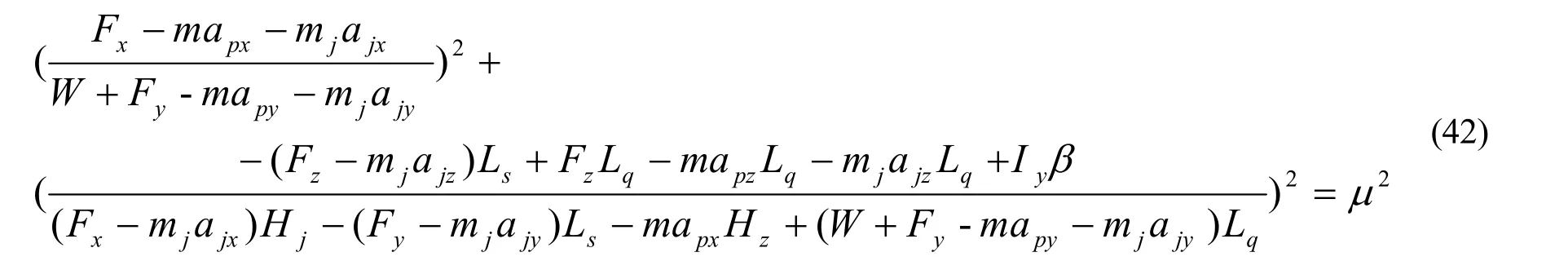
在实际运算中，用（42）式来反推水平输入力的精确数值不太容易，需要解一个二次方程。这里采用数值计算法：优越表逆算法。当表八中最后一栏（tanhφ）趋近于摩擦系数时，加密输入间隔。当表八中最后一栏等于摩擦系数时，逆算输入量准确到一位小数点（或选定位小数点）。

假设乙方有一个针对甲方的水平的初速度1.42（m/s），见图7。

图7　乙方弓步整体动量掤势

有水平初速度的纵向弓步的输入是，

将数据（43）代入稳定公式（16）计算弓步正压力和摩擦力如表9。

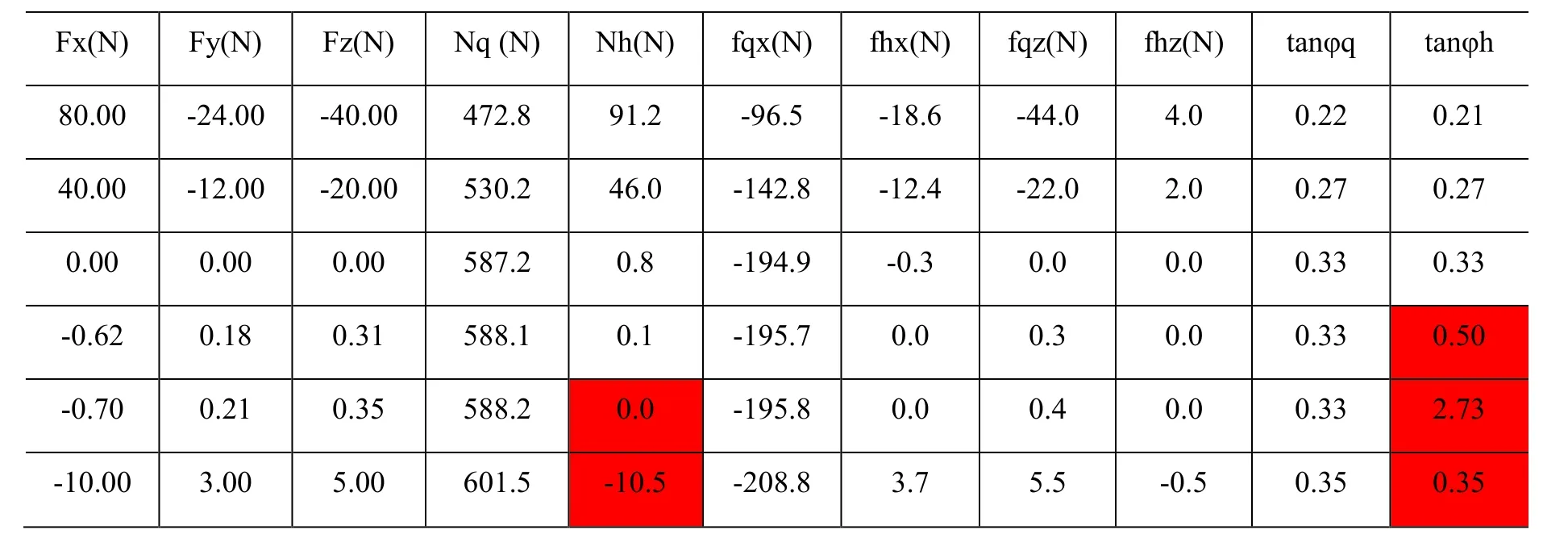
表9　有水平初速度时三维力作用下弓步的正压力和摩擦力

甲方坐步可发的最大水平力、垂直力、横向力的临界力是-570.8：-171.2：285.4牛顿。如果甲方用这样的力捋乙方，乙方将重重跌出。垂直力将使乙方腾空或倒地，水平力和横向力将使乙方飞出或滑出，三力的共同作用将使乙方在失去重心后以跳跃式向甲方横后方向运动。如果甲方用坐步的临界力-570.8：-171.2：285.4牛顿来捋乙方，这全部的力将在三个方向增加乙方的动量。我们可估算一下，假设该力推了作功焦耳。这个功将用来使乙方向横后向运动。乙方在重心跌出后将跳跃式运动。假设一步跳0.5米。每退一步脚打滑0.1米（其实远小于此数）。每一打滑耗能588（重力）×0.5（摩擦系数）×0.1=29.4焦耳。总功除以步功：214÷29.3=7.3步。跳了7.3×0.5=3.64米才把总功用完而止步。这已是市制一丈多了。可见在甲方有初动量时，甲方的动态坐步推手，可将乙方的动态弓步捋出一丈多远。有关太极高手“发人于丈外，令对手挂于墙上”的故事也不是空穴来风。

九、推手的动态效应：动量传递

太极推手是身体之间的接触和碰撞过程，是传递力、整体动量、相对动量三种力源作用的结果。传递力产生的作用属于静态效应，整体动量和相对动量产生的作用属于动态效应，稳定公式（16）描述了这两种效应的总体效应，本节着重讨论动态效应。

仍以甲方“坐步捋”应对乙方“弓步掤”为例，设乙方的“掤劲”里只有全身的整体动量，没有手的相对动量，见图9；甲方的“捋劲”里既有全身的整体动量，又有手的相对动量，见图8。

图8　碰撞前甲方动量

图9　碰撞前乙方动量

掤捋相接就是力学上的碰撞。

甲方捋动乙方的重心后，将所有动量都传给了乙方，见图11，而此时甲方没有了动量，见图10。

由文献［8］知，推手双方的动量会相互传递，一方动量增大时，另一方动量减少，双方的动量总和守恒。因此，甲乙双方碰撞时动量守恒：

其中：

假设甲方攻击乙方的重心，把乙方简化为一个整体，因而乙方没有手的速度和质量。如果运用得当，甲方将所有动量都传给乙方。将代入（44），得

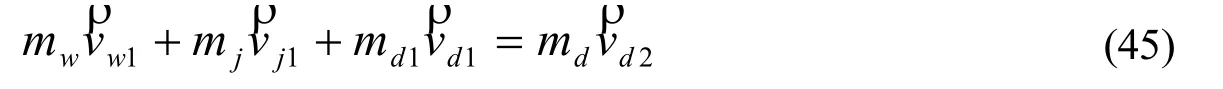
展开成三个分量，

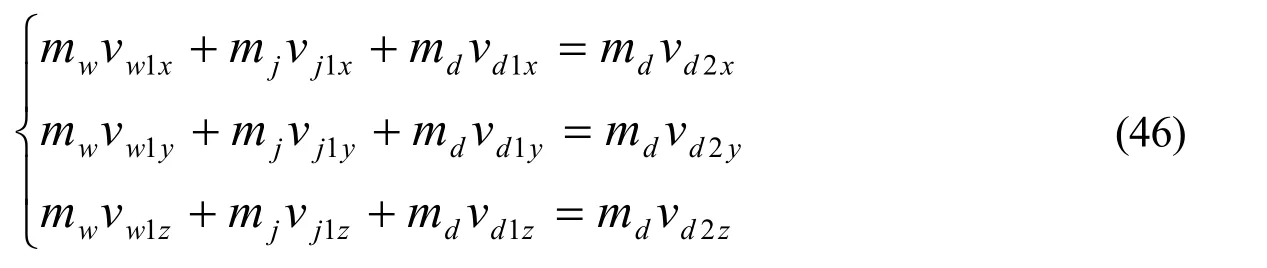
在前述力子中，

图8和图9是碰撞前双方的动量。

将数据（47）代入公式（46）

算出碰撞后的乙方质心速度，

图10和图11是碰撞后双方的动量。可见乙方的速度和动量大为增加。这个速度远远大于1.42（m/s）。如果碰撞后两方脱离，可将（48）代入（16）以分析乙方的稳定度。结果可想而知：乙方由自身的动量打滑，被拔根。计算从略。

图10　碰撞后甲方没有动量

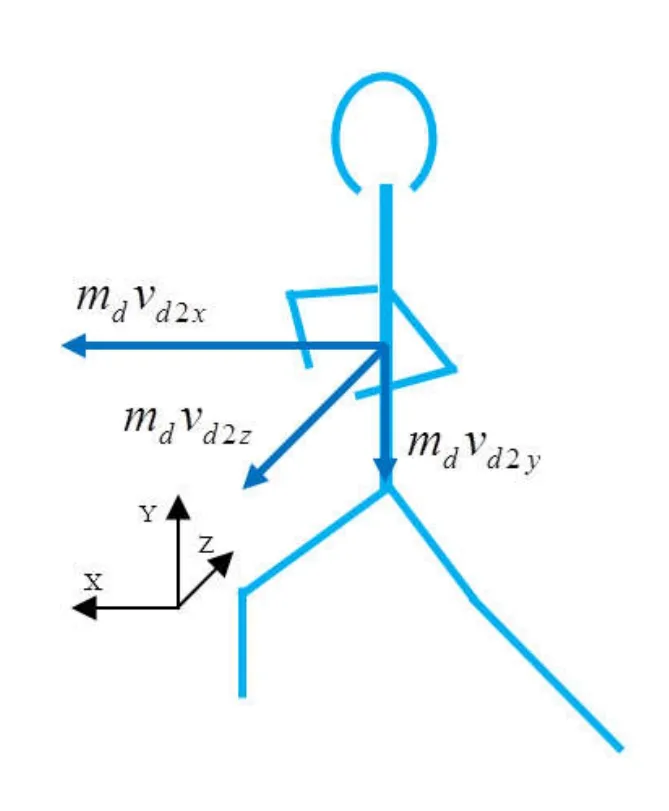
图11　碰撞后乙方动量大增

公式（46）仅包括线性动量的讨论。刚体有线性动量和角动量。角动量是转动惯量和角速度的乘积。一般物体的动量统指该物的线性动量和角动量的综合效果。人体是一个很复杂的体系。某些肢体，例如肘关节和肩关节间的大臂可近似看成一个刚体。另一些肢体，例如肘关节和腕关节间的小臂却无法近似看成一个刚体（因为小臂能旋转）。这些肢体的动量都能用微积分法算出。各肢体通过各关节连成一个整体，各关节帮助各肢体产生相对运动。将所有肢体的动量作矢量叠加，再加入关节本身的动量，就得出人的体系动量。这是理论，真要算得话，需要一台超级计算机。

十、独立模型

上述以弓步和坐步特例和算例，表述了不同情况下平衡和失衡状态的分析方法，说明了稳定、打滑、失根等公式应用的宽泛性和可行性，标定了一些原则。太极拳的动作繁多，各有不同，对具体动作的分析要具体对待。本节分析单腿独立类动作。

图12示出了单腿独立时踢脚的平面模型。单脚在平面内有一定的尺度，地面支持这个尺度。将这尺度简化为与地面接触的两个点。为了模型的统一表述，这两点仍然称为前脚和后脚。踢脚的前一瞬间人体平衡，因而重心通过前后脚的中点。踢脚时和乙方接触的是脚，因而：

Ls-接触（脚）处到重心的水平距离

Hj-接触（脚）处到地面的高度

图12　独立踢脚模型

二维稳定公式（21）成立。

先分析没有速度，只有水平力的情况。一维（水平力）一源（没有速度）时的输入数据是：

将数据（49）代入二维稳定公式（21）计算结果如表10。

表10　水平力作用下单腿独立踢脚的正压力和摩擦力

由于脚宽有限（算式中两脚的间距仅0.1米），独立式的稳定度很差。由表10可见，水平力作用下单腿独立踢脚的临界力很低：前脚失根于牛顿。所以图13所示的水平踢脚法容易引起后倾。

再分析没有速度，只有垂直力的情况。一维（垂直力）一源（没有速度）时的输入数据是：

将数据（50）代入二维稳定公式（21）计算结果如表11。

表11　垂直力作用下单腿独立踢脚的正压力和摩擦力

由表11可见，垂直力作用下单腿独立踢脚的临界力也很低：后脚失根于牛顿。所以图14所示的垂直踢脚法容易引起前倾。

最好的踢脚方向是沿着图12中的JO线。即垂直力和水平力的比例等于接触点的高宽比。按此比例的输入数据是：

将（51）代入（21）计算结果如表11。

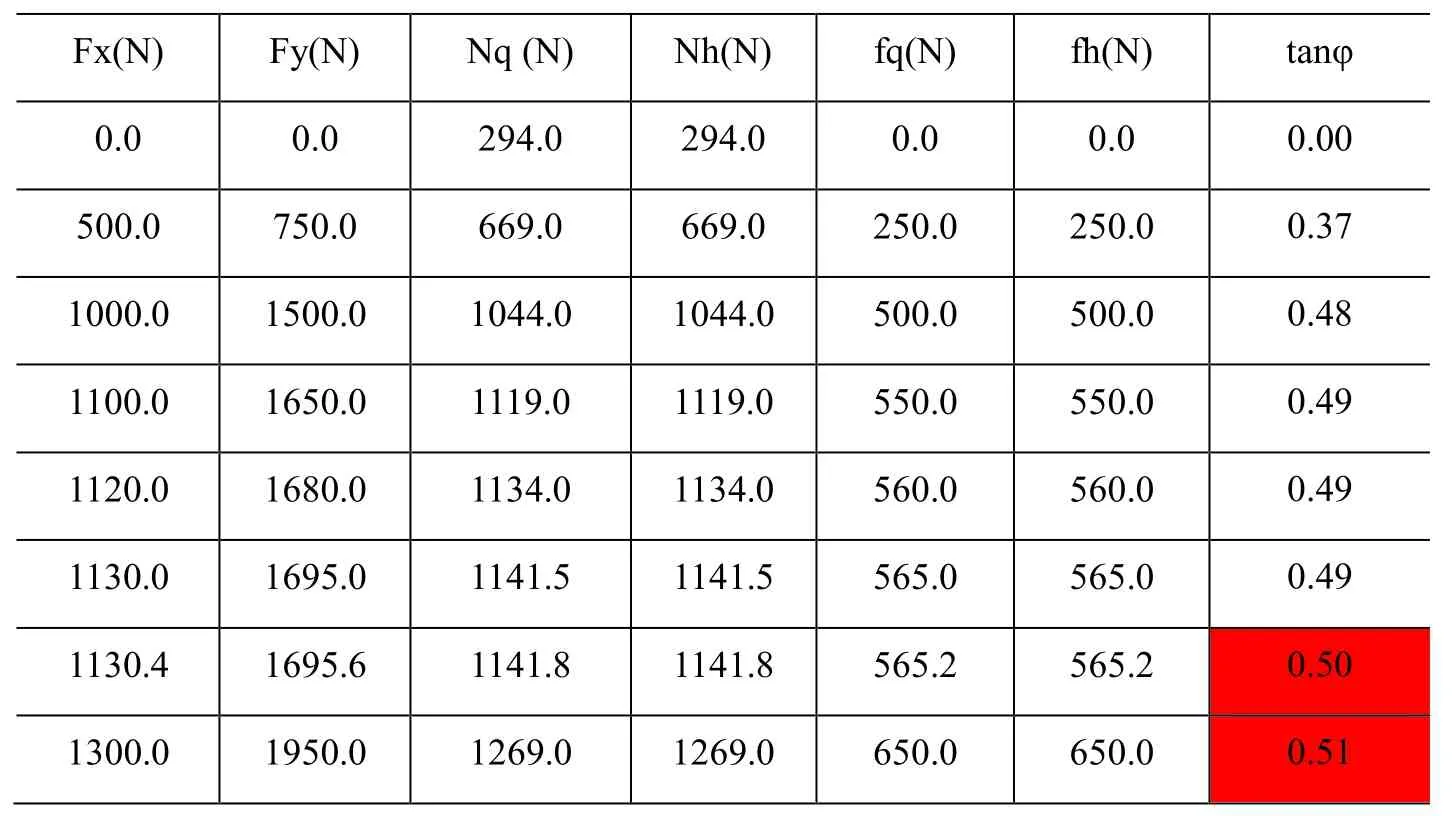
表12　比例力作用下单腿独立踢脚的正压力和摩擦力

由于踢力的方向沿踢脚和站脚的连线，所踢之力全部由地面支持。由表 12可见，前后脚正压力同值递增，永远不会失根。而临界值是双脚（这是站脚的前后边缘）打滑于极高的量值：牛顿。这一脚能踢出牛顿（208公斤）。

比较有效的踢脚方法如图 15所示。先作金鸡独立式，大腿上提至腿面高于水平向前，小腿垂直向下。然后小腿绕膝关节划弧斜踢，脚踢到位时发力的方向尽可能沿踢脚和站脚的连线。

图13　水平踢引起后倾

图14　垂直踢引起前倾

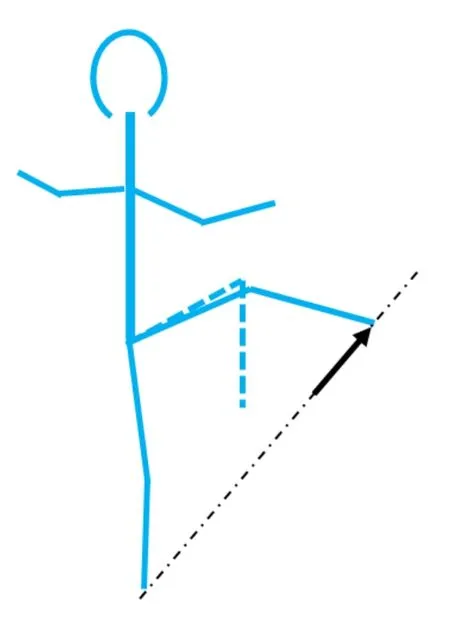
图15　比例踢脚

踢脚一般不用人体质心速度。相对动量将增加踢脚的力度。踢脚的相对速度应沿JO连线。所以，在竞技中踢脚要有一点速度。

［1］顾杰，郭振兴. 太极拳发劲的动量传递解析［J］. 邯郸学院学报，2013（4）.

［2］顾杰，郭振兴. 用人体平面刚体模型分析太极拳在水平作用力下的力学原理［J］. 邯郸学院学报，2015（2）.

［3］Jie Gu. Explosive and Sequential Strength in Tai Chi［J］. T’ai Chi， Vol. 37， No. 3， Fall 2013.

［4］马承九. 太极拳的科学观 ［M］. 台北：东大图书公司，1994.

［5］肖飞. 太极拳的力学原理 ［M］. 北京：人民体育出版社，2009.

［6］顾杰. 太极拳弹簧功［J］. 太极，2015（2-6）.

Analyze Taijiquan under Horizontal， Vertical， and Lateral Force by Rigid Plane Human Model

GU Jie， GUO Zhen-xing， MA Xiu-jie
（Taiji cultural school， Handan College， Handan 056005， China）

proposed a rigid plane human body model under horizontal force. This paper expand the model under vector force with three components， and find three generic and realistic formulas of “equilibrium” and “unbalance critical condition” （“root lost” and “slippery”） for numerical analysis. The model provides mechanical. The model is a mechanical method to normalize Taijiquan posture and technique. The model is used to analyze the mechanics of bow stance， sit stance， foot kick， bow stance bouncing， sit stance pull， etc. The method is demonstrate in various situation. Opponent A and B compete each other in push hand by the mechanical functionality of their postures. “A’s sit stance pulling beat B’s bow stance bouncing” is the conclusion of the classical taiji theory. The three formulas are used to numerically analyze the conclusion. The math calculation shows that for least A can use “four ounce” to “deflect” B’s“thousand pound” out of balance， for most A can through B out for 3 meters. The three formulas found the mechanical foundation for master Wang Zongyue’s quote “Senior can defeat multiple opponents.” Push hand is a competition of the skills， of how to properly use the posture frame. The three formulas are the mathematical tools to analyze push hand.

Taijiquan； mechanical analysis； rigid Human plane model

G852.11

A

1673-2030（2015）04-0092-23

2015-09-05

顾杰（1955—），男，江苏苏州人，邯郸学院太极文化学院客座教授，美国通用汽车公司高级工程师，美国奥克兰大学机械制造博士；郭振兴（1950—），男，河北邯郸人，邯郸学院太极文化学院原院长，高级政工师。华中科技大学铸造机械专业。