高中学生数学类比思维的培养

赖伟英

[摘 要]

类比思维一直是数学学习中不可缺少的一种学习思维。它能让学生通过对A知识内容的学习进而激发出对B知识的学习热情。培养学生的类比思维能让学生猜想与发现结论，从而帮助寻找解题思路。

[关键词]

类比思维;联想;双曲线

从事高中数学教学以来，笔者发现，教师在课堂教学中不仅要创设教学情境，激发学生学习兴趣，还要培养学生诸如逆向思维、归纳思维、整体思维、类比思维等。基于高中数学知识点多且抽象复杂，其定理、概念、性质和解题方法要求学生具有一些数学思维，其中类比思维是学习数学知识与解题中运用较为普遍且有效的思维方式之一。类比思维能让学生通过A知识内容的学习进而激发学习B知识的引路学习方式。如何培养学生的类比思维，运用有效的方法学习高中数学与解题会取到很好的效果。

一、类比思维论述

类比就是由两个对象的某些相同或相似的性质，推断它们在其他性质上也有可能相同或相似的一种推理形式。类比思维是从两个对象之间在某些方面的相似关系中受到启发，从而使问题得到解决的一种创造性思维。类比思维具有联想、启发、假设、模拟等多种功能，在创造性思维中居于重要的地位。

二、类比思维与高中数学学习的关系

类比思想由来已久，我国古代著名木匠鲁班看到带有齿轮状的树叶，他根据类比思想发明了一种砍树工具——锯;还有著名的物理学家牛顿运用类比思维将自由落体运动与天体的运动作比较，最终发现了万有引力定律。在高中数学教学与学习中，教师不妨培养学生的类比思维，运用类比思想深入分析和探讨类比方法在课堂教学中的应用。

首先，教师应当根据教材内容编排的特点，在传授新知识时，可以有意识地引导学生，通过类比思维方法得出所要讲授的新知识，以此慢慢让学生掌握类比推理的方法。其次，教师在对学生进行阶段性知识总结复习时，可以借助相关的知识进行类比，以培养学生对相关知识进行类比的习惯。最后，在对学生讲述如何解题的教学中，教师通过类比引导学生进行推广数学命题或者通过类比，从中寻找解题的途径，以达到深化对题目相关考查知识的理解，从而掌握这些数学思想方法。

三、类比思维的运用——以椭圆、双曲线教学知识为例

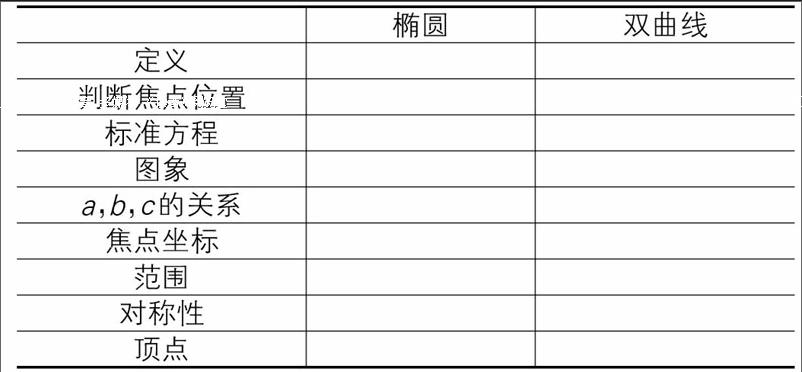
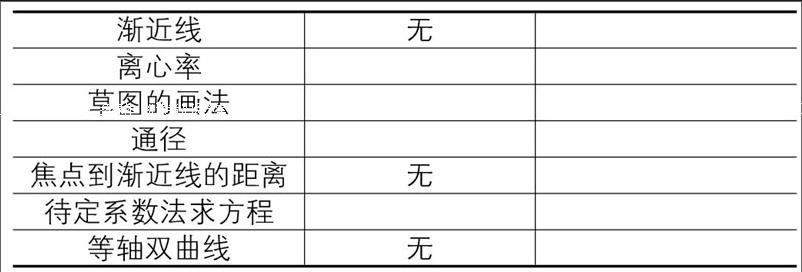
高中学习中，很多知识点学习时可以通过对比学习，这种对比就是常说的类比思维。下面将以圆锥曲线中椭圆、双曲线知识为例，谈谈如何进行类比思维。教师在讲解椭圆和双曲线教学内容的时候，可以展示如下表类比对象。

通过类比二者的不同和相同处，让学生透彻理解并掌握椭圆和双曲线这两个对象的表达式和图像及性质。为了更好的说明类比思维在数学学习中的运用，下面选取椭圆和双曲线部分性质给予论证。

（一）关于焦半径公式的运用

类比思维是创造性思维的一种形式，有时我们可以从一种研究对象的结论出发，往往能创造的喜悦不可思议。焦半径公式在圆锥曲线学习时，会经常使用到。下面用一道例题看看这两个知识有何区别。

例1、已知P（x0，y0）是椭圆[x2a2+y2b2=1]（a>b>0）上一点，[F1，F2]是椭圆的两个焦点，则有|PF1|=a+ex0，|PF2|=a-ex0;类比思考之后，你能得出双曲线类似的结论吗？

其实，在双曲线[x2a2-y2b2=1]（a>0，b>o）[F1（-c，0）]，[F2（c，0）]中，经过论证，有|PF1|=|ex0+a|，|PF2|=|ex0-a|。为了去绝对值，还要再分两种情况：当P在双曲线左支上时，则|PF1||=-（ex0+a），|PF2|=-（ex0-a）;当P在双曲线右支上时，则|PF1||=ex0+a，|PF2|=ex0-a。

此外，对于焦点在y轴的标准方程，可相应将x0换成y0即可得出公式。

教师需要根据把椭圆与双曲线的知识点是紧密联系的，将知识点进行合理迁移，在通过类比得出另一种研究对象的许多意想不到的结论。正如现代美籍匈牙利数学家波利亚曾说过：“如果没有相似推理，那么无论是在初等数学还是在高等数学中，甚至在其他任何领域中，本来可以发现的东西，也可能无从发现。”

（二）根据基本概念与性质推导其他性质的运用

对于椭圆、双曲线的学习，学生一定要掌握这两大知识内容的基本性质。类比思维是合情推理中一种重要的思维方式，学生一定要能利用概念与性质推导出其他性质，从而在数学解题中让题目迎刃而解。下面两道题目对激发学生的解题兴趣很有帮助。

例2、设椭圆[x2a2+y2b2=1]（a>b>0），[F1，F2]是椭圆的两个焦点，点 M为椭圆上除顶点外的任一点，[∠F1MF2=α]，则三角形[F1MF2]的面积[S=b2tanα2]。请证明这个三角形面积。类比思考之后，你能得出双曲线有类似的结论吗？

证明：由椭圆定义得：[MF1+MF2=2a????（1）]

在[△F1MF2]中，由余弦定理可得：

[MF12+MF22-2MF1?MF2cosα=4c2????（2）]

（1）式平方 -（2）式得，

[2MF1?MF2（1+cosα）=4a2-4c2，]

[MF1?MF2=2b21+cosα]，

S=[S=12MF1?MF2sinα=b2sinα1+cosα=b2tanα2]。

同理根据上述性质类比得到双曲线为，点M为双曲线上除定点外的任意一点，

设[x2a2-y2b2=1]（a>0，b>o）[F1，F2]是椭圆的两个焦点，点 M为椭圆上除顶点外的任一点，[∠F1MF2=α]，则三角形[F1MF2]的面积[S=b2cotα2]。（证明过程略）

基于在这道题的结论中，椭圆与双曲线的两个面积公式的不同之处仅在三角形的正切与余切的区别，可以说这种形式的不单单是圆锥曲线性质规律性的一种反映，更是在对比学习中，运用类比方法能很好的让题目迎刃而解。

例3、已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为[kPM]、[kPN]时，那么[kPM]与[kPN]之积是与点P的位置无关的定值。试对双曲线[x2a2-y2b2=1]写出具有类似特性的性质，并加以证明。

解题分析：类似的性质为若MN是双曲线[x2a2-y2b2=1]（a>0，b>o）上关于原点对称的两个点，点P是双曲线上任意一点，当直线PM、（下转第60页）（上接第53页）PN的斜率都存在，并记为[kPM]、[kPN]时，那么[kPM]与[kPN]之积是与点P的位置无关的定值。

证明：设点M、P的坐标为（[m ，n]）、（[x ，y]），则N（[-m ，-n]），其中[m2a2-n2b2=1]。

因为点M（[m ，n]）在已知双曲线[x2a2-y2b2=1]（a>0，b>o）上，所以由[kPM]=[y-nx-m]，[kPN]=[y+nx+m]，得[kPM]·[kPN]=[y-nx-m]·[y+nx+m]=[y2-n2x2-m2]，

因为点M（[m ，n]）在已知双曲线[m2a2-n2b2=1]上，所以[n2=b2a2m2-b2]，因为点P（[x ，y]）在已知双曲线[x2a2-y2b2=1]上，所以[y2=b2a2x2-b2]，代入得[kPM?kPN=b2a2?x2-n2x2-m2=b2a2]（定值）。

四、反思与总结

瑞士数学家欧拉曾说过：“类比是伟大的引路人”。在高中数学学习中，学生能合理地运用“类比”方法，对数学学习是十分有益的。本文选取圆锥曲线中椭圆与双曲线的类比教学，不难发现两个教学内容有许多相似之处，案例中运用类比方法可以引导学生提出问题、进行探究，在学生思考中慢慢培养其类比思维。

[参 考 文 献]

[1]邓益阳.探究一类新型题的解题策略[J].高中数学教与学，2004（2）.

[2]徐永忠.解析深化理性思维考查的数学高考[J].数学通报，2004（11）.

[3]王忠维.椭圆与双曲线——奇妙的类比[J].数学大世界（教师适用），2011（12）.