偶数阶巴特沃斯高通滤波器优化设计与仿真

张　露，林开武

( 1．铜陵职业技术学院电气工程系，安徽铜陵244000; 2．铜陵有色股份铜冠信息科技有限责任公司，安徽铜陵244000)



偶数阶巴特沃斯高通滤波器优化设计与仿真

张露1，林开武2

( 1．铜陵职业技术学院电气工程系，安徽铜陵244000; 2．铜陵有色股份铜冠信息科技有限责任公司，安徽铜陵244000)

摘要:对二阶压控电压源巴特沃斯高通滤波器的设计进行了理论推导，给出了通用表达式，并在此基础上设计了四阶单位增益的高通滤波器;通过Multisim 10仿真软件对设计的高通滤波器进行了仿真，研究了电路中电容间容值的不同比值k对设计的高通滤波器幅频特性的影响，指出不同位置电阻、电容的变化对滤波器特性的影响不同，为不同位置的电阻、电容精度的选择提供依据，由此指导偶数阶巴特沃斯高通滤波器的设计．

关键词:巴特沃斯;高通滤波器;偶数阶;单位增益

滤波器根据滤波范围可将其分为低通、高通、带通与带阻4种滤波器，实际使用中只能逼近理想特性．常用的逼近方法有巴特沃斯响应和切比雪夫响应等［1］，巴特沃斯高通滤波器因具有通带内幅频响应平坦而被广泛使用，其常见的电路形式主要有无限增益多路反馈式和压控电压源式［2］．目前，压控电压源式高通滤波器的设计主要有查表法［3，4］、图示法［5］和计算法［6］等，但这些方法都存在一些不足，比如有些设计是先确定电阻，再匹配电容［6］，但特定电容难找，订制时间长、成本高，且电容精度也较电阻难以保证;一些查表法、图示法和一些计算法没有给出必要的理论根据和计算通式，使用者难以采用［7］．文献［2］针对上述问题提出了二阶压控电压源巴特沃斯高通滤波器的优化设计方法，但并未提及二阶以上的偶数阶巴特沃斯高通滤波器的优化设计，此处在此基础上并借鉴文献［8］，以四阶高通滤波器设计为例说明二阶以上偶数阶巴特沃斯高通滤波器的设计．

1二阶高通滤波器设计

偶数阶高通滤波器可以由二阶高通滤波器通过级联的方式获得，所以二阶滤波器是设计高于二阶的偶数阶滤波器的基础．常用的二阶高通滤波器的电路形式如图1所示．

根据文献［2］，由图1可知其传递函数为

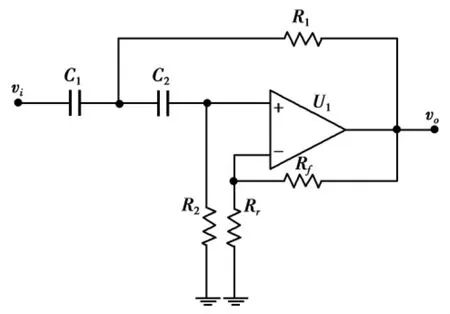
图1二阶高通滤波器电路

其中，

二阶归一化高通滤波器传递函数为

假设电容C1，C2成比例关系，即C1=kC2，由式( 4) ( 5) ( 6)得到关系式

式( 7)是关于R2的二次方程，因为R2是电阻，有实数，另，k，0，C2均大于0，AF≥1，所以

因此可解得

同理可得

由上述推倒过程可知，若知道电容C1，C2的值，便可根据( 9) ( 10)式选定R1，R2的值，尤其是单位增益的高通滤波器，因为此时AF=1，即当Rr≥Rf，可近似满足要求．另外为运放负端提供地回路，同时补偿运放失调，此时Rf‖Rr=R2，又因Rr≥Rf，所以Rf≈R2．这样二阶高通滤波器中的所有电阻、电容都一一确定了．

2四阶单位增益巴特沃斯高通滤波器的优化设计

四阶巴特沃斯高通滤波器由两个二阶巴特沃斯高通滤波器级联得到，且在实际使用中，特别是有关信号分析的应用中经常使用的是通带内放大倍数稳定为1的单位增益巴特沃斯高通滤波器［2］，所以以单位增益高通滤波器设计为例，即AF=1，如果要设计放大倍数大于1的高通滤波器，只需改变Rf与Rr的比值就可以了．由此式( 7)变为－k0R2C2+( 1+k)=0，可得

将式( 11)式带入到式( 6)可得

设计实例:设计四阶压控电压源单位增益巴特沃斯高通滤波器，截止频率为100 kHz，增益G=1，电路仿真图如图2所示:

图2仿真电路

当k=1时，对应不同C1值分别为0．1 nF，1 nF，2．2 nF和10 nF时，电路中其他元件参数如表1所示:

表1　 k=1时不同电容值对应的电阻值

不同C1下该滤波器的幅频特性曲线如图3所示．由图3可知，当k值为1，取不同的电容值时，得到的滤波器幅频特性基本重合，即电容的改变对此种情况下的滤波器影响几乎没有．并且由这种取值得到的四阶巴特沃斯高通滤波器具有较理想的幅频特性．

3不同k情况下的幅频特性

上述的取值方法最简单，并且电容值的变化对滤波器的幅频特性也几乎没有影响，另外电容C1=C2= C3=C4，电容元件的规格就一种，订货和装配都比较方便，成本也可以降低．但这种取值的幅频特性曲线是不是最好的一种，还需研究．取两级k值相同，不同k值对应的电阻、电容如表2所示．

表2不同k时电路中其他电阻取值

R3，R7阻值很大，均取值为1 MΩ，R2=R4，R6=R8，这样仿真电路中的所有元器件的参数均已获得，得到的幅频特性如图4所示．

图3 k=1时不同电容下的幅频特性

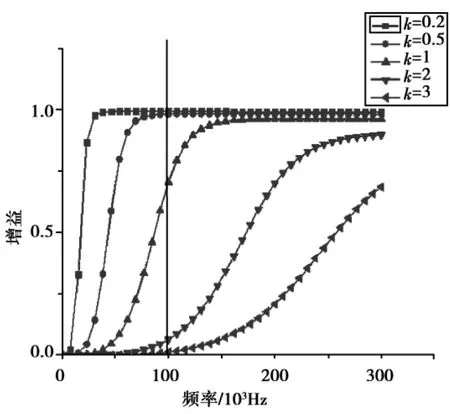
图4不同k值下的幅频特性

由图4可知，k的取值大于1时幅频特性曲线变得平坦，而且k值越大越平坦，截止频率越大，选频特性越差．当k的取值小于1时，幅频特性变得陡峭，但是截止频率变小，随着k的取值越小，曲线越陡峭，截止频率越小，也越不符合设计截止频率为100 kHz的要求．只有当k的取值为1时最理想，最符合要求．由此可推广为设计高于二阶的偶数阶高通滤波器时，每个二阶滤波器的k值应均取值为1．

4元件数值变化对幅频特性的影响

为了突出电路中各元件数值变化对设计的高通滤波器幅频特性的影响，考察电路中各电容、电阻按+20%和－20%变化的情况．由于电阻R3，R7为大值电阻，这里不考虑这两个电阻阻值的变化，并且所有取值是在k为1时所得．得到的幅频特性曲线如图5，图6所示．

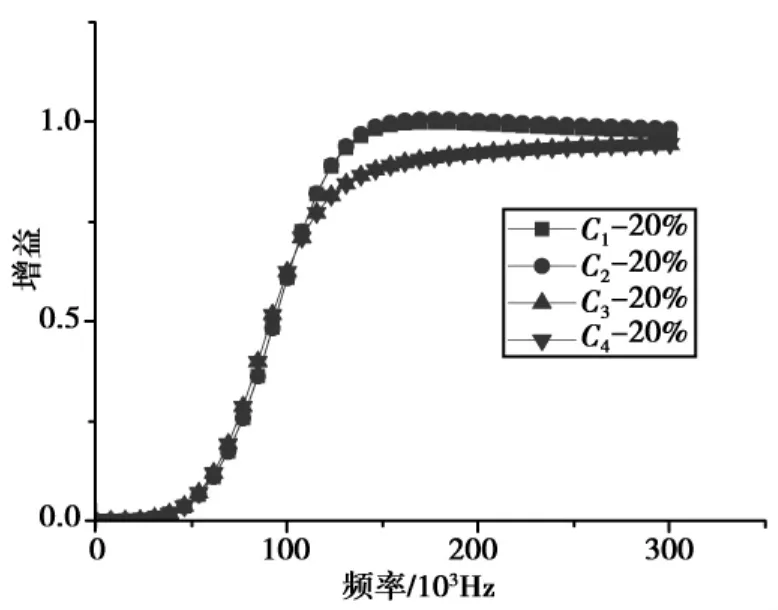
图5各电容值减小20%

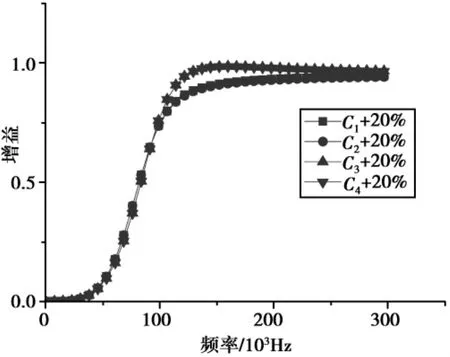
图6各电容值增加20%

由图5和图6可知，当电容值减小和增加时，其幅频特性曲线较好，只是电容C3，C4值减小20%和C1，C2增加20%时其增益略小于1，其他两种情况电容值的变化对幅频特性的影响很小，所以在选择电容时应注意电容值的变化方向，即比标准所需值增大还是减小．

由图7可知，当电路中的电阻减小时，其幅频特性的增益都减小，并且R6的影响最大，此时增益已经减小到0．75左右．而由图8可知，当电阻阻值增加时，幅频特性较好，增益也维持在1附近，同样只是R6增加时影响最大，所以在选择电阻时，要特别注意R6，选择精度高的电阻．其他电阻的选择应向电阻值变大的方向选择，以减少由于电阻的变化对设计的高通滤波器性能的影响．

图7各电阻值减小20%

图8各电阻值增加20%

5　结束语

将高于二阶的偶数阶高通滤波器优化设计归结为n个二阶高通滤波器的优化设计方案，不仅计算简单、元件规格少、成本低，且具有稳定的优点．此处设计了一个四阶单位增益巴特沃斯高通滤波器，通过Multisim 10对设计的滤波器进行了仿真，研究了不同k值情况下的滤波器幅频特性，还仿真分析了电路中电阻、电容值的变化对高通滤波器幅频特性的影响，发现电阻变化对性能影响较电容明显，所以在元器件选择时需要注意．该方法对偶数阶高通滤波器的实际应用具有一定的参考价值．

参考文献:

［1］高明甫，杨勇，孔令斌．二阶压控电压源低通滤波器设计［J］．电子技术，2010( 3) : 73-75

［2］郑园，杨勇，贾东亮，等．压控电压源二阶巴特沃斯高通滤波器的优化设计［J］．电子技术，2012( 2) : 34-37

［3］JOHNSON D E，JOHNSON J R，MOORE H P．A Handbook of active filters［M］．New Jersey，1980

［4］谢自美．电子线路设计实验测试［M］．武汉:华中科技大学出版社，2006

［5］D E·约翰逊，J R约翰逊．有源滤波器精确设计手册［M］．李国荣，译．北京:北京电子工业出版社，1984

［6］秦世才，王朝英．集成运算放大器应用原理［M］．天津:天津人民出版社，1983

［7］杨勇，刑磊，诸远奇，等．压控电压源2n阶单位增益巴特沃斯低通滤波器优化设计［J］．电子学报，2011( 8) : 1894-1897

［8］林开司，张露．巴特沃斯低通滤波器优化设计与仿真研究［J］．重庆工商大学学报:自然科学版，2014，31( 6) : 58-62

Optimal Design and Simulation of Even-order Butterworth High-pass Filter

ZHANG Lu1，LIN Kai-wu2

( 1．Department of Electrical Engineering，Tongling Vocation and Technical College，Tongling 244000，China; 2．Tongling Nonferrous Tongguan Information and Technology Company Limited，Tongling 244000，China)

Abstract:The design of Butterworth high-pass filter of second-order voltage-controlled voltage source is derived theoretically and a common expression is given．On the basis of the design the forth order unity-gain low-pass filter is designed．The high-pass filter is simulated by Multisim10 simulation software．Influence of the ratio k between the capacitance in the circuit on amplitude-frequency characteristics of the high-pass filter is studied．It is indicated that changes of resistance and capacitance in different positions influence filter’s characteristics differently．

That is a basis for precision selection of resistors and capacitors in different positions to guide the design of even-order Butterworth high-pass filter．

Key words:Butterworth; high-pass filter; even-order; unity-gain

作者简介:张露( 1983-)，女，广西桂平人，讲师，硕士，从事电子测控技术、数字图像处理技术研究．

*基金项目:安徽省高等学校省级自然科学研究项目( KJ2011B187)．

收稿日期:2014-08-30;修回日期: 2014-10-10．

doi:10．16055/j．issn．1672－058X．2015．0005．0021

中图分类号:TN713．4

文献标识码:A

文章编号:1672－058X( 2015) 05－0089－05