基于Flexsim与遗传算法的混流生产线仿真与优化研究*

邱伊健，涂海宁

（南昌大学机电工程学院，南昌 330031）

基于Flexsim与遗传算法的混流生产线仿真与优化研究*

邱伊健，涂海宁

（南昌大学机电工程学院，南昌 330031）

以某企业汽车后桥生产线为研究对象，运用Flexsim仿真软件建立了混流生产线的仿真模型，对瓶颈问题、生产线平衡等问题进行了优化。同时结合遗传算法以最小化闲置与超载时间为目标，优化了混流生产线的投产序列。使得混流生产线的各项性能指标均得到了提升，同时有效地降低了企业生产成本。证明了运用Flexsim软件与遗传算法相结合，是一种成本较低却效果显著的分析方式。为企业生产线的实际运行提供了理论依据，为优化改进生产线提供了新的方法。

Flexsim；生产线优化；遗传算法；投产序列

0 引言

随着市场竞争的日趋激烈，现代生产企业为了适应多变的市场需求，逐渐形成了基于订单的多品种、小批量的混流生产模式。特别是生产汽车及其部件的企业，多采用混流生产线。混流生产线生产的产品大多是一个系列、多种类型的，产品在生产作业方式和工艺流程上基本是相同或相似的。但是，混流生产线由于工序复杂、产品种类较多而常常导致生产率较低等问题。因此，寻求一种有效的方法对已有生产线进行优化改善，成为摆在企业面前的一个重要问题。

文献［1］运用工作研究中的时间研究和程序分析法，提出了生产线的优化方案，并运用Witness软件仿真，评价了优化效果；文献［2］中提出了一种基于遗传算法的仿真优化方法，同时开发了基于QUEST仿真系统的算法实例，最后通过与国外仿真优化软件OptQuest作对比证明了优化方法的有效性；文献［3］提出了基于蒙特卡洛法的生产线混杂系统的优化仿真计算方法，对生产线进行了数值仿真计算，仿真结果验证了方法的可行性和有效性；文献［4］将Petri网模型与Flexsim仿真结合起来，将Petri网模型转化成为Flexsim仿真模型，得到了一种高效的生产线仿真优化方法。

本文利用Flexsim仿真与遗传算法相结合对生产线进行优化分析，既有效地分析了生产线的问题，消除了瓶颈，同时又得到了较优的投产序列，很好地节约了成本。

1 本生产线仿真与优化方案

1.1 Flexsim简介

Flexsim是近年来一款新型的三维仿真软件，具有面向对象的特性和三维可视化的优点，可方便地建立模型并通过仿真进行效果评价［5］。在软件图形开发环境中，用户可方便地使用已有对象搭建3D仿真模型，同时软件允许使用者建立自己的模型对象来满足相关需求。Flexsim仿真对象中内带了大量可设置参数，同时用户可以使用c++编程来扩展已有的参数功能来实现复杂的逻辑。其优点在于建模调试简单方便，模型扩展性强，使用价格相对便宜［6-7］。

Flexsim仿真过程一般分为三个部分：首先对实际生产流程进行简化，除去对于生产流程无关或者对生产过程影响不大的细节；接着建立仿真模型，包括模型的布局、相关模块间的逻辑关系，然后确定参数以及相关程序的编写；最后运行仿真模型，同时对仿真结果进行分析。

1.2 遗传算法求解排序问题

遗传算法是一种模拟自然界的自然选择与遗传机制的仿生算法。通过模仿生物的进化过程，根据选择、交叉及变异来搜索解的空间［8］。算法对产生的每个染色体进行评价，依据每个染色体的适应性进行选择，最后经过反复迭代，得到最终收敛。

1.2.1 适应度函数

适应度函数也称作评价函数，是算法中的关键部分，用来衡量在优化中能达到或接近最优解的程度。对于求解排序问题以求得最小值的问题，算法搜索空间中的适应度函数F（f（x））与解空间中的目标函数f（x）间的转换可表示为：

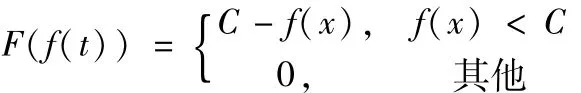
其中，C是f（x）的估计最大值，是一个相对较大的数。1.2.2 遗传算法编码及算子设计

一个染色体编码，即为一种排列顺序，代表一种生产线投产方案的可行解，由数字1、2、3、4等代表；同时，选用轮盘赌［9］作为遗传算法解决生产线排序问题的选择算子；算法采用单点交叉算子，将选择出的两个个体作为父染色体并且交换两者的部分基因来进行单点交叉，父染色体交叉后，剔除染色体中与交叉部分重复的基因来保证子代染色体仍为可行解；变异算子能防止算法收敛于一个局部最优解，因此变异算子采取随机交换排列顺序中两个不同位子上的产品。

1.3 研究方法与步骤

基于Flexsim仿真软件与遗传算法对混流生产线进行仿真优化的方法与步骤如图1所示。

图1 基于Flexsim与遗传算法的生产线仿真优化方法

首先分析生产线的生产状况，得到生产线的基础数据，如产量、工时和生产节拍等；接着建立生产线的Flexsim模型，根据基础数据设定相关参数，最后通过运行模型得到仿真结果，来确定生产线的瓶颈；在此基础上，结合工业工程等方法对瓶颈工位进行改善；同时建立产品投产序列的数学模型，基于遗传算法利用Matlab编程求得投产序列的最优解；最后再次利用Flexsim进行优化方案的评估，评价优化效果；进而实施优化方案。

下面以某家汽车车桥制造企业为例，进行实例的研究分析。

2 案例分析

2.1 生产线的背景及生产现状

X公司是一家国家重点生产汽车驱动桥的专业化国有企业。该企业产品种类很多，产量也大不相同，其中后桥生产线的产量相对较大，工序较多，经常出现无法在班次时间内完成额定生产计划的情况，导致工人经常加班，生产成本大量提高。因此，本文选取该公司的后桥生产线作为研究对象，针对提升产能和降低成本等问题，对该生产线进行仿真优化。

该后桥生产线根据市场需求生产4种型号的汽车后桥，这里分别命名为A、B、C、D。根据企业单日生产计划可知4种型号的产品计划产量分别为A型225台，B型150台，C型150台，D型75台。令每种产品的计划产量除以最大公约数，即可知一个最小生产循环生产3台A型后桥、2台B型后桥、2台C型后桥、1台D型后桥。生产线工位流程图如图2所示。

图2 某企业后桥生产线工位流程图

2.2 相关基础数据的确定

对车间生产线上的MES系统（生产执行系统）中工位采集的实时的时间点作出时间差，将所得数据进行统计分析，求出平均值，得到实际生产中4种产品在生产线上的作业时间，如表1所示。

表1 混流生产线各工位作业时间表

同时，工人单日班次的有效工作时间为7h30min，因此生产线的平均生产节拍C为：

其中T为计划班次的有效工作时间；Ni为生产计划中第i种产品的计划产量；n为计划生产的产品品种数。

依照企业生产计划的安排，产品进入装配线的投产顺序简单制定为A-B-D-C的依次顺序。

3 基于Flexsim的生产线仿真

3.1 仿真模型的建立

各地情况千差万别，农村生态环境治理的目标如何考虑现实，反映差别？《行动计划》明确，各地要根据环境质量、自然条件、经济水平和农民期盼，科学确定本地区整治目标任务，集中力量解决突出环境问题，不搞“一刀切”，不搞形式主义。

以该后桥生产线为仿真对象，按照生产线的实际布局情况建立起仿真模型。

首先在模型中添加所需的模块，4种类型的产品由Source对象产生，装配差速器和制动器的工位采用合成器Combiner进行合成，其他加工工位由Processor对象定义，同时下线点设置一个吸收器并放置一个缓存区Queue进行返工处理；最后依照各工序的工艺流程关系选择连接方式连接各个模块。为方便显示，将现实生产线的直线布局显示成双线布局形式，最后建立起的仿真模型如图3所示。

图3 仿真模型布局图

3.2 仿真参数的设置

模型建立后，根据所收集的基础数据设置模型的参数。投产顺序在上游工位对象中设置。打开对象的参数对话框，在到达方式中选择“按序列表到达”，在序列表中用4种实体类型1、2、3、4分别代表4种产品A、B、C、D，现有方案在单次生产循环中的投产顺序为A-A-AB-B-D-C-C因此在序列表中表示为1-1-1-2-2-4-3-3。

各工位的处理时间根据表1中的作业时间来确定，并在工位参数设定时，添加如下代码：

case n：return Tjn；

其中n=1，2，3，4，代表第n种产品；Tjn代表第n种产品在第j（j=1，2，3……8）个工位上的处理时间，如果Tjn=0，代表该种产品在该工位上没有装配操作。

仿真运行过程中，需重复进行75（225，150，150，75的最大公约数）次最小生产循环，当产量到达计划产量600台时终止仿真。因此，在第一个工位中添加如下代码：

then closeinput ports of the current object；

所有参数设置完成后，对模型进行编译，最后运行模型。模型运行效果如图4所示。

图4 模型运行效果图

3.3 仿真结果及分析

仿真模型运行过程中，读取工位1和工位2的运行状况分析图（图5），可知工位1与工位2的阻塞率分别高达30.5%和60.5%。同时仿真结束后，导出各个模型实体的利用率，如图6所示。

图5 工位运行状况图

图6 改善前生产线各工位利用率

分析仿真结果可知：后桥生产线中工位利用率最高的是工位“装制动器总成带半轴组件”，而且各个工位的利用率差异较大，而前面几个工位的工位阻塞率相对较高，因此可知，工位“装制动器总成带半轴组件”是整条生产线的瓶颈工位，整条生产线平衡性较差；同时，仿真运行时间为35614.4s，高于生产线单日班次时间，并且根据计算可得，生产线最小生产循环中的闲置与超载时间总和高达1747.9s。因此改善瓶颈工位，同时找到一个方法解决生产线的平衡问题就显得很重要了。

4 生产线改善及投产序列优化

4.1 瓶颈工位的改善

为解决瓶颈工位的问题，笔者引进了“ECRS”工序分析四大原则：取消、合并、重排、简化［10］，对瓶颈工位进行动作分析，如图7所示。

图7 ECRS原则改善瓶颈工位

通过在生产线上对工位“装制动器总成带半轴组件”及附近工位的观察和确认，发现左制动器安装时，由于公差技术要求，需要在制动器带半轴安装在桥壳上的同时添加垫片来控制间隙，而放置垫片的物料架被安置在离工人3-4步距离的位置，这样，该工人在选取垫片时，动作幅度较大，移动距离较长，并且垫片数量选取不合适的话需要重复选取。而右制动器安装时则不需要安装垫片。因此，安装左制动器的工人常常比安装右制动器的工人慢大约15～20s，导致工位的整体作业时间过长，而下一个工位“安装手制动拉索”由于工序较为简单，因此常处于闲置状态。

根据以上对瓶颈工位的分析，可知该工位左右操作时间不均衡。为解决该问题，将该工位的工序细分，如图，依据ECRS原则，对工序进行重排：对于产品A、B、D，将安装左制动器时拧紧制动器螺丝的工序分配至下一个工位“安装手制动拉索”处；装配产品C时，由于没有“安装手制动拉索”工位，则让此工位闲置的工人专门进行拧紧螺丝的工作。这样，使得安装左制动器的整体时间与安装右制动器的时间基本持平。

同时，根据动作经济学原则（如图8），对制动器与垫片放置的相对位置进行重新布置，使得工人选取垫片时由原先的离开3～4步改进为现在的只需转身便可取拿。这样改善以后，使得瓶颈工位“装制动器总成带半轴组件”的作业时间由59.1s降至39.8s，虽然下一个工位的作业时间有所增加，但是超载大大减少，整体的平衡性有了很大改善。同时合理地安排了闲置工人的工作。

图8 动作经济学原则改善瓶颈工位

另外对于工位利用率相对较高的工位“主减速器总成进桥”由于是一个工人完成作业，也存在阻塞，平衡性较差。对此，可以将该工位的两道工序拆分，将第二道工序“拧紧桥壳大法兰面10个螺钉”单独作为一个工位，交予另外的工人负责操作。而第一个工位“上线点”的工作较为简易，经常出现闲置，根据ECRS原则可将第二个工位“桥壳大法兰面安装螺栓及涂胶”与第一个工位进行合并，让上线点的工人上线的同时负责完成大法兰面安装螺栓与涂胶工作，同时将原第二个工位的工人安排至新增的工位，进行拧紧大法兰面螺钉的工作。

这样改善后，工位“主减速器总成进桥”的作业时间由原来的45.6s降至22.9s，新增工位“拧紧桥壳大法兰面螺钉”的作业时间为23.5s。虽然总时间变化不大，但是临近工位的阻塞得到了改善，整体平衡性得到了提高（见图9）。

图9 工位“主减速器总成进桥”的改善

经过改善后的产品、工位和作业时间对应的矩阵如表2。改善后生产线的平均生产节拍为39.8s。

表2 改善后工位作业时间矩阵

4.2 基于遗传算法的投产序列优化

瓶颈工位改善之后，笔者希望再通过简单的遗传算法框架构建数学模型来求得最优的产品投产序列方案，从而改善企业当下根据计划数量简单随意投产的情况。

4.2.1 投产排序的数学模型

首先确定目标函数。由于优化的目标是为了使生产保持均衡，尽可能缩小每一个工人完成的工作量的差异，减少闲置与超载；同时根据上一章的分析可知，生产线改善前闲置与超载时间过高。因此本文将一个最小生产循环中闲置与超载时间总和最小化设置为目标函数。

在一个生产循环内，共有8个后桥。当第v（v=1，2，3…8）个后桥进入第j个工位时，用Sjv表示第v个后桥在第j个工位上装配的开始时间，加工时间Tjv可根据图 得知，因此可知结束时间为：

操作工在工位j完成了第v个后桥的装配工作后回到起点，准备装配生产循环中的第v+1个后桥，这时存在2种情况：

（1）工位闲置：当Ejv小于等于生产节拍C'时，操作工人提前完成了装配，此时出现工位闲置，且下一个后桥的开始时间：

（2）工位超载：当Ejv大于生产节拍C'时，操作工人未能在生产节拍内完成装配，此时出现工位超载，且下一个后桥的开始时间：

结合以上2种情况可知：一个生产循环内，第v个后桥进入第j个工位的开始时间Sjv应该为Sjv=max｛0，Ejv-1-C'｝；并且，第v个后桥在第j个工位上的工位闲置时间IdleTjv=max｛0，C'-Ejv｝；第v个后桥在第j个工位上的工位超载时间OvertTjv=max｛0，Sjv+Tjv-C'｝。由此，本文的目标函数可确定为：

4.2.2 根据遗传算法和Matlab软件求最优解

根据表2中的数据，设置Matlab编程的相关参数。同时，初始设定群体规模为20，交叉概率为0.85，变异概率为0.1，设定最大繁殖代数为500代，适应度函数如下：

最后经过500代进化后获得全局最优解，最优解的序列为13231421，故得到最佳的投产序列应为ACBCADBA，对应的最小的空闲时间与超载时间之和为734.2s。适应度函数随代数的变化如图10所示。

图10 适应度函数值变化图

5 优化效果评价

最后，对于生产线改善后的方案，再次运用Flexsim仿真来对其效果进行评价。设置好相关参数后，运行仿真模型。模型运行结束后，得到仿真运行时间为24077s，大大低于优化前的仿真运行时间，满足单日班次时间的范围，提高了生产线的产能。

同时可以导出改善后工位利用率（图11）。根据仿真结果可知，各个工位利用率都达到50%以上，有了很大的平衡，整条生产线的平衡率由原来的64.8%提高到了82.7%，同时瓶颈工位得到了有效的改善。

图11 改善后生产线各工位利用率

此外，生产线根据求得的最佳投产序列得到了最小的空闲与超载时间，比改善前的1747.9s减少了1013.7s，平均下来每生产一个后桥就能节约127s，按40元/小时的人工成本，每个后桥可以节省1.41元，按15万件/年的年产量计算，仅后桥线一年累计就可节省大约21.15万元的直接人工生产成本。

6 结束语

生产多种型号产品的混流生产线是一个复杂的动态离散系统。对于企业而言，如何有效地改善已有生产线使之达到高效率、低成本显得十分重要。本文充分利用了Flexsim中面向对象的特性，运用Flexsim软件对某企业后桥生产线进行仿真，建立了三维可视化模型，发现了生产瓶颈和严重的生产线平衡问题，对此提出了相关改善方案，有效地改善了瓶颈问题和生产线平衡问题。同时通过遗传算法合理地安排了生产线的投产顺序，有效地减少了闲置与超载，为企业取得了较好的经济效益。

［1］祁丽霞.基于工作研究的厢式半挂车焊装生产线优化［J］.现代制造工程，2013（6）：69-72.

［2］刘亮，郭宇，顾婷，等.面向生产线仿真模型的优化技术研究［J］.机械制造与自动化，2007，36（1）：10-13.

［3］程曙，张浩，樊留群.基于生产线优化配置的混杂系统建模与仿真 ［J］.计算机集成制造系统，2006，12（10）：1577-1580.

［4］杨银，路春光，陈金鹏，等.采用Flexsim的生产系统建模与仿真研究［J］.现代制造工程，2009（12）：42-46.

［5］Averill M L.Flexsim User Guide［M］.Utah：Flexsim Software Products，Inc，2003.

［6］王雪兰，常治斌，唐秋华，等.基于Flexsim的混流生产线生产顺序仿真 ［J］.湖北汽车工业学院学报，2007，21（4）：50-52.

［7］Nordqren W B.Flexsim simulation environment［J］.Simulation Conference，2003（1）：197-200.

［8］余晓光，严洪森，殷乾坤.基于Flexsim的车间调度优化［J］.计算机技术与发展，2010，20（3）：44-47.

［9］苏平，于兆勤.基于混合遗传算法的混合装配线排序问题研究［J］.计算机集成制造系统，2008，14（5）：1001-1007.

［10］贡怡峰，周炳海.汽车空调管路生产线瓶颈改善研究［J］.组合机床与自动化加工技术，2008（11）：1-4.

（编辑 赵蓉）

Research on Simulation and Optim ization of the M ixed-model Production Line Based on Flexsim and Genetic A lgorithm

QIU Yi-jian，TU Hai-ning
（School of Mechanical Engineering，Nanchang University，Nanchang 330031，China）

Focusing on a company's car rear axle production line，simulationmodelof themixed-model production line is built w ith Flexsim software，the problems such as bottleneck and line balancing are optimized.Then，to achieve the target thatminim izing idle time and overload time，we use the genetic algorithm getting a better production sequence of themixed-model production line.So that the performance indicators of the production line are improved，and the company's production costs are effectively reduced. Proved that combining Flexsim software and genetic algorithm is a kind of analyticalmethod that are low cost and efficient，it provide a theoretical basis to the actual operation of the production line，and provide a new method to optimize and improve the production line.

flexsim；production line optimization；genetic algorithm；production sequence

TH16；TG65

A

1001-2265（2015）08-0119-05 DOI：10.13462/j.cnki.mmtamt.2015.08.031

2014-10-27

国家自然科学基金（50905083）

邱伊健（1992-），男，江西抚州人，南昌大学硕士研究生，研究方向为制造过程管理，（E-mail）893879165@qq.com。