基于蒙特卡洛的地铁车门系统可靠性分析

石奋义，高旭东，邢宗义，王学慧

（南京理工大学a.机械工程学院；b.自动化学院，南京210018）

基于蒙特卡洛的地铁车门系统可靠性分析

石奋义a，高旭东a，邢宗义b，王学慧b

（南京理工大学a.机械工程学院；b.自动化学院，南京210018）

客室车门是城轨车辆系统重要组成部分，车门运行的可靠性直接影响城轨交通的运营质量。文章结合某地铁2号线的车门故障历史记录，采用蒙特卡洛方法对车门系统故障进行可靠性分析。首先对车门系统进行故障模式分析，建立了车门系统故障树；其次运用蒙特卡洛方法对车门系统进行可靠性进行仿真分析。最后确定了系统的薄弱环节，为可靠性设计和故障诊断提供了依据。

可靠度；车门系统；蒙特卡洛；故障树分析

0 引言

随着城轨交通的快速发展，城轨列车的安全愈发受到关注。车门系统作为城市轨道车辆的重要组成部件，结构复杂。城轨列车正线运行时车门开启、关闭频繁，车门系统长时间工作容易引起车门系统零部件损坏，导致车门故障，影响乘客乘车安全和列车的正常运行。因此有必要对车门系统进行可靠性分析，找出其薄弱环节，提高系统可靠性。

近年来国内外学者采用不同的方法对车门系统可靠性进行了研究。朱小娟［1］等通过建立传统故障树的方式分析车门系统，运用故障树定性、定量的分析方法得出车门系统故障的薄弱环节；董军哲［2］通过建立基于GO法的可靠性模型，分析得出引起车门故障的所有因素，并确定系统的薄弱环节。以上文献通过故障树分析法找出系统的薄弱环节，但该方法随故障树建模规模的呈几何增长的缺点，不适用于大型复杂系统。蒙特卡洛方法本身作为一种仿真方法在工程上应用广泛［3-4］，同时与故障树分析法相结合可以找出系统的薄弱环节。朱永梅［5］等在故障树分析的基础上，建立了蒙特卡洛仿真模型，找出了影响系统的薄弱环节，提高了系统的可靠性。周爱萍［6］把蒙特卡洛与故障树结合对特种车辆的液压系统的可靠性进行分析，得出底事件的重要度以及系统可靠度指标。

目前为止，尚未检索到将蒙特卡洛方法运用到车门可靠性分析的相关文献。故本文将蒙特卡洛方法应用到车门系统故障树分析首先建立车门系统故障树模型，求解出系统的失效分布函数，其次运用蒙特卡洛对车门系统进行可靠性分析，最后得出影响车门系统可靠性的薄弱环节。

1 车门系统故障树分析

故障树分析，就是通过建立以确定的系统故障事件为顶事件，按照由顶事件至底事，以直接造成故障事件的可能因素为枝干，以不能分解的零部件的故障模式为枝叶建立故障树［7-8］。

1.1 车门系统的故障树建立

以车门系统故障为顶事件，对某地铁2号线历史故障数据进行分析，找出了引起车门故障的各级底事件。顶事件失效主要由五个中间事件所引起分别是门控信号错误M1、电机无动作M2、车门切除故障M3、解锁故障M4、关门阻力大M5这，其他中间事件分别是：门控保持电路失效M6、无开/关门信号M7、EDCU功能失效M8、安全回路故障M9、解锁信号错误M10、润滑不足M11、机构卡滞M12、，故障树如图1，其底事件如表1所示。

图1 车门系统故障树分析

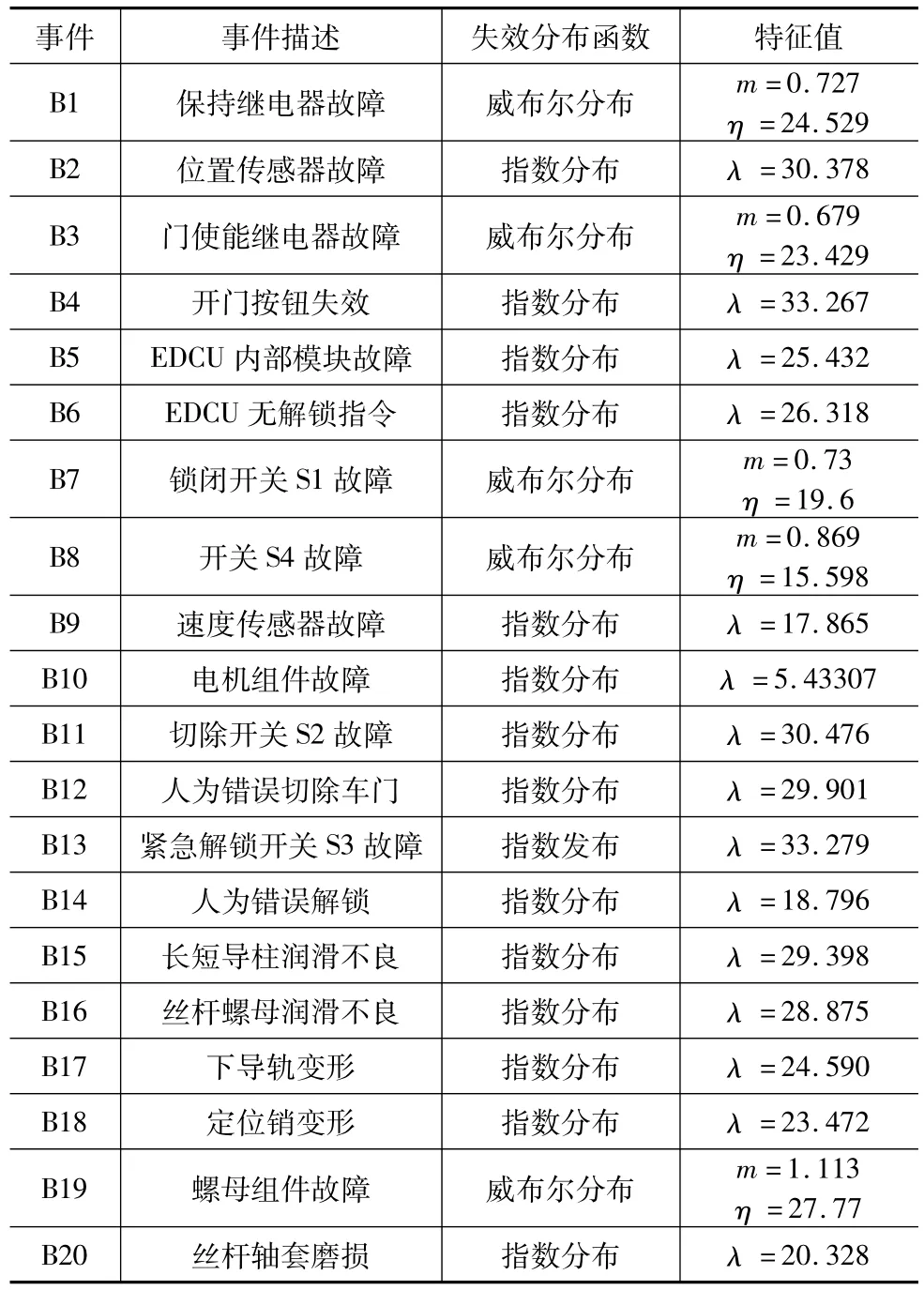
表1 车门各基本事件分布函数及参数

1.2 车门系统故障树定性、定量分析

故障树分析从两方面来研究：定性分析和定量分析；定性分析用于求解导致故障树中顶事件发生的最小割集。最小割集是导致顶事件发生的最少的顶事件的组合，当且仅当最小割集中的全部元件发生故障时，系统才出现故障。所以找出复杂系统的最小割集对消除潜在故障以及指导系统检修工作颇有现实意义。

常用的求最小割集的方法有两种：下行法和上行法，本文依据下行法，得到车门系统故障的全部最小割集为｛B1｝，｛B2｝，｛B3｝，｛B4｝，｛B5｝，｛B6｝，｛B7｝，｛B8｝，｛B9｝，｛B10｝，｛B11｝，｛B12｝，｛B13｝，｛B14｝，｛B18｝，｛B19｝，｛B20｝。

定量分析在于求解出系统的顶事件的发生概率和关键重要度：①根据已知各底事件的发生概率计算出顶事件的发生概率，是各基本事件概率相加的分析方法。②求出各底事件或各最小割集的关键重要度，根据关键重要度的大小确定薄弱环节。

由于大型复杂系统其故障树最小割集数目较大，以传统方式计算顶事件发生概率和关键重要度时，计算比较费时费力，因此本文引入蒙特卡洛法计算系统的可靠性指标，从而确定出系统的薄弱环节，本方法需要统计出各底事件的失效概率函数见表1。

2 蒙特卡洛可靠性仿真分析

2.1 蒙特卡洛算法原理

蒙特卡洛法［9］又称统计模拟方法，它是以概率统计理论为基础的近似计算方法，其基本原理是：某事件的概率可以用大量试验中该事件发生的频率来估算，当样本容量足够大时，可以认为该事件的发生频率即为其概率。应用到实际工程时先对影响其可靠度的随机变量进行大量的随机抽样，然后把这些抽样值代入到失效函数中，确定结构是否失效，多次计算后从中求得结构的失效概率。

2.2 仿真模型建立

设整个系统为S，其包含的n个事件z的集合

对于每一个事件，其概率分布函数都符合一定的统计规律，文中所建立的20个底事件的概率密度函数及其特征参数如表1。

设底事件Zi的随机事件在某时刻t的状态为xi（t），则可用二项分布表示其分布规律：

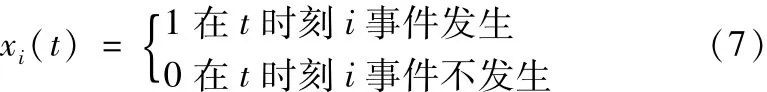
则底事件Zi在t时刻发生的概率pi（t）为随机事件的期望值xi（t），即

若定义φ（t）为Y（t）=（x1（t），x2（t），…xn（t））的函数，那么顶事件的状态S（t）也可用底事件来表示，顶事件在t时刻发生的概率为ps（t），即

2.3 仿真过程

（1）利用各基本事件失效分布函数对每个基本事件进行抽样。对第i个基本部件失效时间抽样值为：

式中η为（0，1）之间的随机数。

（2）假设系统内部有k个最小割集，每个最小割集中有n个基本部件。则第q个最小割集中n个基本事件对应的抽样时间为ti（i=1，2，…n）。最小割集中所有底事件发生才会导致这个最小割集发生，只有确定第q个最小割集中所有底事件发生的最大时间，才可以求出这个最小割集发生时间tq，即

（3）只要有一个最小割集发生，顶事件就会发生，只要求出k个最小割集的最小发生时间，即可求出顶事件发生的时间Y，，即：

（4）重复（1）、（2）、（3）步骤M次，就可以得到M次仿真结果Ym（m=1，2，…M），将其依次与事先给定的M个时间tm（m=1，2，…M）进行比较，若Ym＜tm，则顶事件在给定时间内发生，即说明系统失效。累积tm时刻内失效次数Nm。仿真流程图如图2所示。

图2 仿真流程图

2.4 仿真统计指标

系统可靠性指标包括两部分基本部件重要度和基本部件模式重要度。

（1）基本部件重要度W（Bi）

用W（Bi）表示部件Bi在系统中的重要程度，若W（Bi）=1则说明只要部件Bi发生一次失效则系统必定因其失效而发生一次故障，说明此部件的重要程度较高。

（2）基本部件模式重要度WN（Bi）

用模式重要度WN（Bi）来判断系统可靠性的薄弱环节，部件WN（Bi）越大，说明越是系统可靠性薄弱环节。

3 仿真实验

本文结合某地铁2号线故障历史数据，仿真得出重要度结果如表2所示。

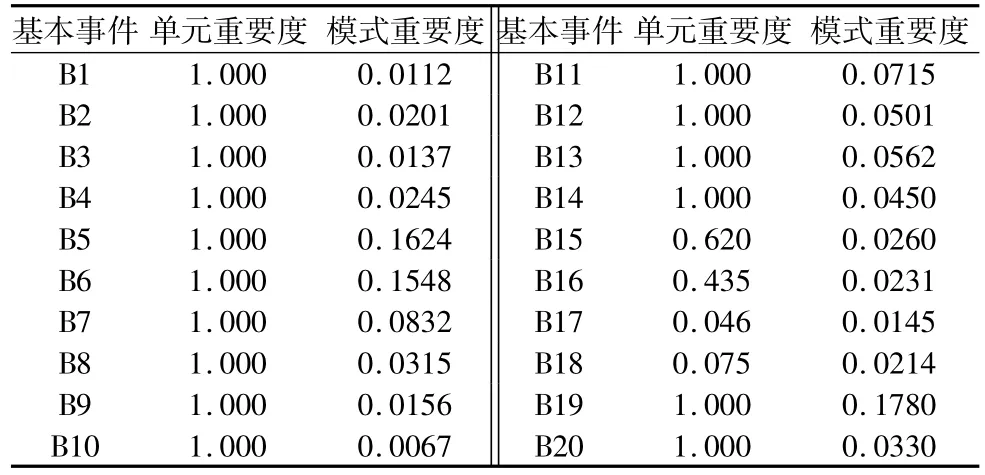
表2 仿真结果分析

由部件重要度定义可知，若其值等于1，则代表只要部件B i，则说明只要部件B i发生一次失效，系统必定因器失效而失效。由表2可以看出除了B15、B16、B17、B18外其余底事件单元重要度都是1，部件为1的底事件与前面定性分析计算的最小割集是一致的，验证了系统仿真的正确性。

模式重要度表示了部件B i失效而引起系统失效的次数在系统总失效数中的百分比，因此部件重要度越大，说明部件B i越是可靠性的薄弱环节。从表2可以看出B5、B6、B7、B19对应的模式重要度值较大，说明这四个事件是系统的薄弱环节，即EDCU内部模块故障、EDCU无解锁指令功能失效、行程开关S1破损、和螺母组件故障，与其他资料的统计的结果一致［10］，说明了仿真结果的正确性。因此要提高车门系统的可靠度就要从这几个薄弱环节入手，在系统维护和设计中重点考虑。

图3为系统可靠度仿真曲线，由图可以看出车门系统可靠度随着工作时间增长而下降，这与车门系统实际情况相符合，说明系统仿真的正确性。

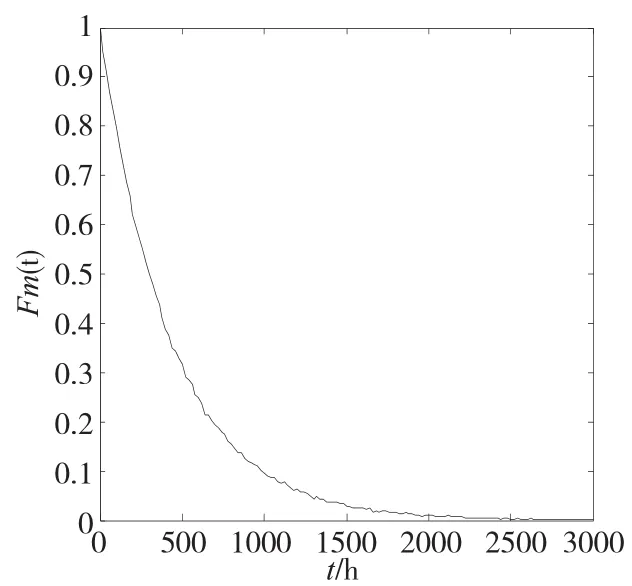
图3 可靠度曲线

4 结论

本文通过蒙特拉洛可靠性分析，找出了系统中引发故障的关键部件，EDCU内部模块故障、EDCU无解锁指令功能失效、行程开关S1破损、和螺母组件故障。此方法与传统故障树方法相比简单、效率高极大的节省了地铁公司很大的人力和财力，也容易被操作人员掌握和使用。统计结果与现场检修工程师经验保持一致，将为地铁车门的故障诊断与改进设计提供技术支持。

［1］朱小娟，王建兵，印祯民.上海地铁车辆客室车门可靠性技术研究［J］.城市轨道交通研究，2006，9（3）：31-34.

［2］董军哲，杨建伟，黄强.基于GO法地铁车辆客室车门可靠性评价［J］.城市轨道交通研究，2013，16（4）：28-31.

［3］Ejlali A，Miremadi SG.FPGA-based Monte Carlo simulation for fault tree analysis［J］.Microelectronics Reliability，2004，44（6）：1017-1028.

［4］Deak P，Van Straten M，Shrimpton PC，etal.Validation of a Monte Carlo tool for patient-specific dose simulations in multi-slice computed tomography［J］.European radiology，2008，18（4）：759-772.

［5］朱永梅，黄静，张宇.基于故障树分析的船用齿轮箱的可靠性仿真［J］.江苏科技大学学报 （自然科学版），2012，26（4）：350-355.

［6］周爱萍，王显会，宋子健.基于故障树分析法的大型特种车辆液压系统的可靠性仿真分析［J］.机床与液压，2011，39（19）：151-154.

［7］全达，孙秀芳，王缅，等.基于故障树分析法的识别单元可靠性分析［J］.现代制造工程，2012（4）：122-125.

［8］苏国强，李小宁，滕燕.气动点焊伺服焊枪实验平台及故障模式研究［J］.机械制造与自动化，2012，41（2）：37-40.

［9］杜比.蒙特卡洛方法在系统工程中的应用［M］.西安：西安交通大学出版社，2007.

［10］夏军，邢宗义，王晓浩.基于FTA的地铁车门故障诊断研究［J］.组合机床与自动化加工技术，2014（4）：76-78.

（编辑 赵蓉）

Reliability Analysis of the Subway Door System Based on M onte Carlo

SHIFen-yia，GAO Xu-donga，XING Zong-yib，WANG Xue-huib
（a.School of Mechanical Engineering；b.School of Automation，Nanjing University of Science&Technology，Nanjing 210018，China）

The passenger compartment door is an important part of the train system，the operating reliability of which affects the quality of rail transport system.In this paper，failuremode of the door system is analyzed and the fault tree of the door system is established based on the fault history of the door system from Guangzhoumetro line2.Firstly，door system failuremode is analyzed and the door system failure tree analysiswas built.Secondly Monte Carlo methods are introduced to simulate the reliability of door system.The results identify the weaknesses in the system and could provide technical support for the reliability design and fault diagnosis.

reliability；door system；Monte Carlo；FTA

TH166；TG506

A

1001-2265（2015）08-0104-03 DOI：10.13462/j.cnki.mmtamt.2015.08.027

2015-03-29

国家高技术研究发展计划（863计划）（2011AA110501）

石奋义（1989-），男，山东济宁人，南京理工大学硕士研究生，研究方向为可靠性与交通控制，（E-mail）fenyishi123@163.com。