基于多轴同步滑模控制的积分分离PID算法的研究*

基于多轴同步滑模控制的积分分离PID算法的研究*

程文雅，罗 亮，刘知贵
（西南科技大学信息工程学院，四川绵阳 621010）

为了提高多轴系统之间的同步性能，采用积分分离PID算法来解决传统耦合同步控制算法的增益常数难以确定的问题。多轴间的同步误差先经过积分分离PID预处理再引入到滑模控制的切换函数中。使得滑模控制律的设计中不仅有系统的位置误差又包含系统的同步误差，同时为了保证了滑模运动的动态品质滑模运动采用指数趋近律。基于Lyaunov稳定性分析原理证明了设计算法的渐进稳定性。最后与无耦合补偿的双轴系统比较，验证了所设计算法不仅能保证单轴系统的运动性能，而且还有效的提升了多轴间的同步性能。

积分分离PID；耦合补偿；滑模控制；多轴同步

0 引言

随着自动化程度的加深，人们的生产和生活与机器人的联系更加密切，因而对机器人的控制也提出了更高的要求。尤其是随着工业化的快速发展，工业机器人［1］逐渐替代人力劳动被越来越广泛的应用。在很多场合下要求机器人的各轴之间协调同步控制，从而达到更高的控制精度保证系统的可靠性，使系统的整体性能达到最优［2-3］。通常在机器人的控制中，每个运动轴单独被控制，各个轴之间不相互接收信息。各轴扰动引起的误差也仅靠自身的闭环反馈去调节，其它轴不能做出相应的补偿。各执行机构之间不能同步协调控制必然会影响系统的整体性能，甚至会因为不协调运动导致各轴受力不均衡，从而过度磨损系统机构的严重后果。

1980年由美国密歇根大学Y.Koren针对双轴运动平台率先提出交叉藕合同步控制方法［4］。在该控制算法中，充分考虑了被控对象之间的相互影响作用，将两者之间的偏差经过比较之后反馈给各自的控制器，进行调节，补偿。这种方案有效的改善了多轴系统的同步性能，大大提高了跟踪精度，逐渐成为多轴系统同步运动控制的标准模式。滑模变结构控制是变结构控制的一种控制策略，其滑动模态是可以设计的，且与系统的参数及扰动无关，因此具有很好的鲁棒性。近年来滑模变结构控制理论在机器人控制领域中被广泛应用。1983年，J.J.Slotine等［5］首次采用滑模控制方法设计了二自由度刚体机械手的滑模变结构控制器，实现了时变参考轨迹跟踪的控制。Z.H.Man等针对多关节机器人设计了Terminal滑模控制器，使各关节按指定时间进行位置跟踪。A.Ficola等采用滑模控制方法，通过设计两个滑模面，实现了带有一个弹性力臂的两关节机器人控制［6］。

对补偿算法研究之后将交叉藕合和滑模控制相结合，并在交叉藕合补偿器设计中运用积分分离的PID算法，克服了传统交叉藕合补偿增益难以确定的缺点，不仅提高了系统的同步性能而且减小了系统的超调量。最后二自由度机器人验证了该算法的有效性。

1 多轴同步的概念

协调同步控制问题在多变量控制系统中广泛存在。在多变量控制的实践中，有很多场合需要受控对象的控制过程互相配合和“协调”，使各个变量之间保持某种协调关系，使整个系统处在技术上合理、经济上合算的协调工作状态中。可以分为以下几类：

（1）同步关系是各受控量应满足某种线性和非线性的函数关系：

（2）常用的比例关系：

当比例关系ui=1时，也即为最简单的同步关系。

（3）各控制变量之间保持一个恒定差

以下部分所分析设计的同步控制类型是依据上述第二种最基本的同步类型，而且比例系数是1，即完全同步的情况。

2 机器人动力学模型

设在不考虑摩擦和外界扰动的情况下，对于一个二自由度串联机器人，在各关节上有力转矩作用时，应用拉格朗日方法建立的机器人动力学名义模型［7］如下：

其中M（）q为正定质量惯性矩阵，H q，˙（）q为哥氏力、离心力和重力之和。

实际对象为：

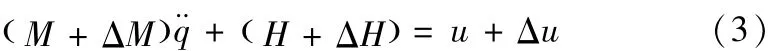
将建模误差、参数变化及其它不确定因素视为外界扰动f（）t，则

其中：

3 控制律的设计

3.1 滑模控制律的设计

滑模控制实际上是一种特殊的非线性控制，突出表现在控制的不连续性。其在动态过程中，根据系统当前的状态（偏差及其各阶导数等）有目的地不断变化，迫使系统按照预定的“滑模模态”运动。滑模运动包括趋近运动和滑模两个过程。系统从任意初始状态趋近切换面，直到到达切换面的运动称为趋近运动。而滑模的可达性仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，而对于趋近运动的具体轨迹未做任何限制，采用趋近律的方法可以改善趋近运动的动态品质［7］。在分析了滑模运动的实质之后综合考虑了这两种运动，最后运用指数趋近律的方式来提高系统的性能。

在控制律设计中，由于f是未知的，取f的估计值为fc且f的上下界为fL和fH。

在以下的分析设计中，以双力臂单关节机器人来设计控制律。为了改善系统的性能，在设计过程中，不仅考虑单关节臂的位置误差，同时引入两关节的同步误差。即：

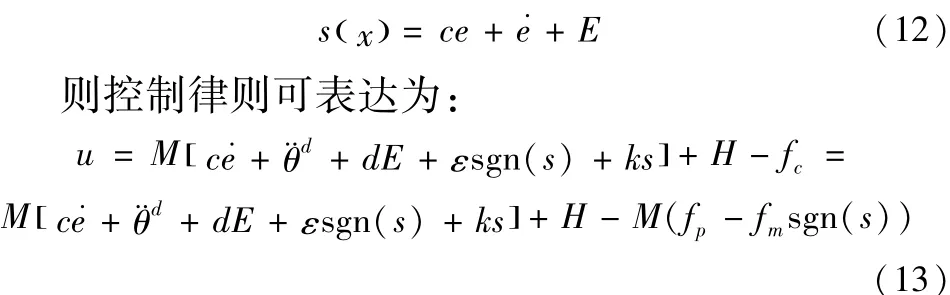
在设计滑模运动的指数趋近律时，为了保证快速趋近的同时消弱抖振，尽量使参数ε取较小的值，而增大k的取值［9］。

收敛性是保证控制算法获得良好控制性能的基础，而稳定性是保证系统正常运行的前提。对以上所提出来的滑模控制的收敛性证明如下：

3.2 积分分离PID的设计

积分分离的核心思想是：当系统偏差较大时，取消积分的作用，减小由于积分作用引起的超调量，提高系统的稳定性；当偏差接近设定值时，引入积分作用，消除静差，提高精度。其控制算法可表示为：

式中ε是人为的设定一个阀值，满足ε＞0；β为积分项的开关系数。当时，β=1；当时，β=0。

其中所设计的积分分离PID算法的输入是两关节之间的同步误差，且阀值取ε=0.01。

4 同步控制系统建模

在MATLAB中，Simulink是用来建模、仿真和分析动态多维系统的交互工具［10-11］。在对所设计的结构分析之后，采用Simulink搭建控制系统的结构，具体的算法设计采用S函数编写实现。机器人同步控制系统模型如图1所示。

单轴运动控制系统滑模控制器设计框图如图2所示。

藕合补偿控制器采用积分分离的结构，其模型如图3所示。

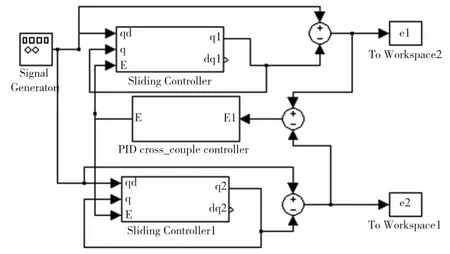
图1 机器人双轴同步控制系统模型

图2 单轴运动控制系统框图

图3 积分分离的PID结构框图

5 仿真数学模型及参数

第一个关节的模型的动态方程为：

第二个关节的动态方程：

其中两者方程中的外界扰动f（）t均取高斯噪声模型，如下所示：

其中b=0.80，c=4。

控制律采用式（15），取c=20，ε=0.3。仿真的结果如下。

由图5～图7可以看出，设计的基于藕合补偿的积分分离PID算法加快了系统的响应时间，有效的减小了系统的超调量，而且各轴能够准确有效的跟踪设定的轨迹，大大减小了跟踪误差。由图8看出两轴之间的同步误差平稳的收敛，最大的超调量也控制在±0.03内。与图9无藕合补偿的算法进行比较，所提出的算法在起步时具有较好的同步性，并且在整个过程中，减弱了振荡作用，控制效果稳定。保证了位置调节品质的同时，同步性能也得到了大大的提高。

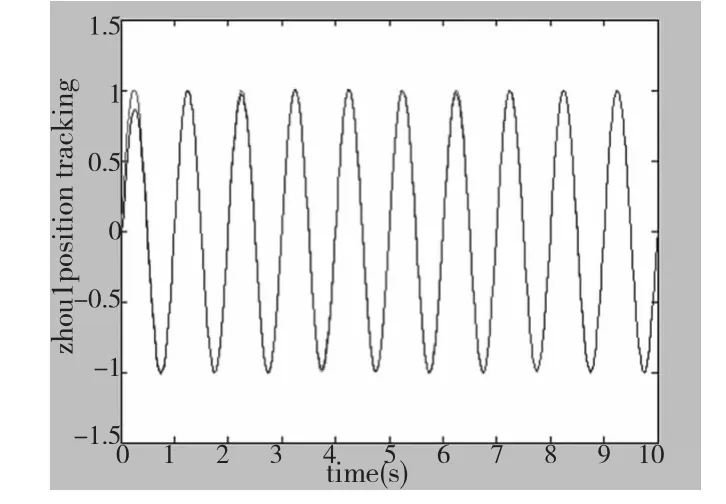
图4 轴1的位置跟踪图

图5 轴1的位置跟踪误差

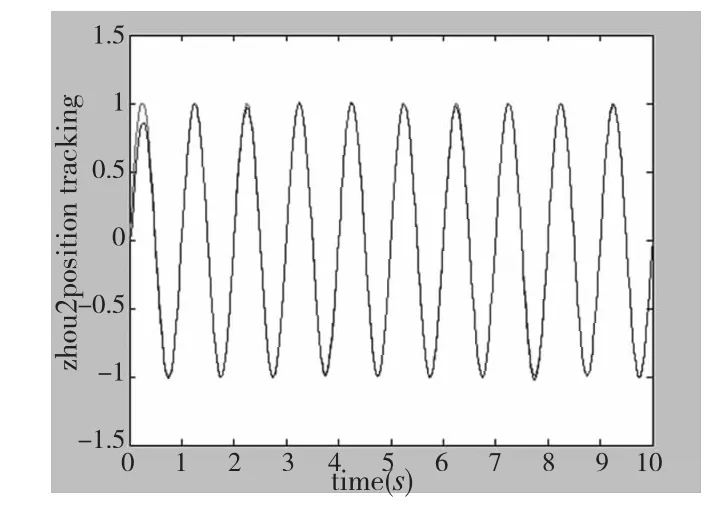
图6 轴2的位置跟踪图

图7 轴2的位置跟踪误差

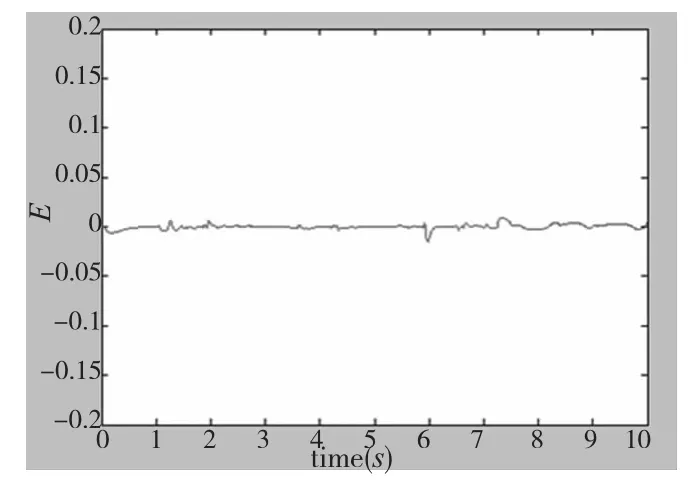
图8 轴1和轴2间的同步误差

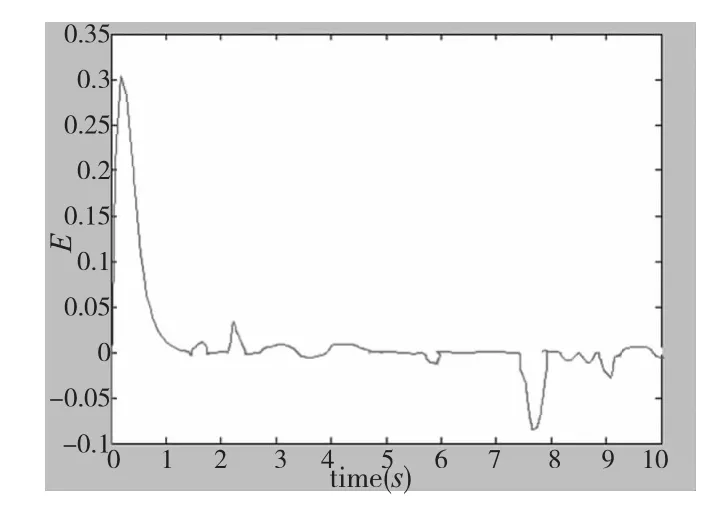
图9 无耦合补偿两轴间的同步误差

6 结论

经过分析补偿对比将积分分离PID控制运用到藕合补偿的控制回路，将多轴之间的同步误差先经过处理，再引入到滑模控制律的设计中，使整个系统不仅作用位置误差的影响同时还考虑轴间的同步误差，所设计的控制算法能够使位置误差和同步误差都收敛到零附近。有效的实现了双轴间的同步协调运动。所设计的算法与以往常规的滑模控制策略相比，先将同步误差经过积分分离处理，更加精确有效的实现系统的跟踪和同步性能。

［1］马光，申桂英.工业机器人的现状及发展趋势［J］.组合机床与自动化加工技术，2002（3）：48-51.

［2］李小彭，刘春时，马晓波，等.数控机床加工精度提高技术的进展及其存在的问题［J］.组合机床与自动化加工技术，2010（11）：1-4.

［3］高恒路，桑勇，邵龙潭.同步控制策略及其典型应用的研究［J］.液压气动与密封，2012，32（5）：1-7.

［4］Sun D，Shao X，Feng G.A model-free cross-coupled control for position synchronization ofmulti-axismotions：theory and experiments［J］.Control Systems Technology，IEEE Transactions on，2007，15（2）：306-314.

［5］Slotine J J，Sastry SS.Tracking control of nonlinear systems using sliding surfaces，with application to robot manipulators.Internat［J］.Control，1983，38（2）：465-492.

［6］刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展［J］.控制理论与应用，2007，24（3）：407-418.

［7］杨亚辉，苏玉鑫，张立科，等.机器人系统同步协调自适应控制［J］.系统仿真学报，2008，20（1）：117-119.

［8］王祝炯.滑模变结构控制系统设计方法研究［D］.杭州：浙江工业大学，2003.

［9］武成龙.基于滑模变结构的同步控制器设计［D］.哈尔滨：哈尔滨工业大学，2013.

［10］孙红涛，潘海鸿，陈琳，等.基于自适应滑模变结构控制的多轴同步协调控制系统建模［J］.组合机床与自动化加工技术，2013（1）：68-73.

［11］高晓丁，左贺，任高阳，等.基于智能PI控制的多电机同步传动系统［J］.电气传动，2007，37（11）：39-41.

（编辑 赵蓉）

Based on the M ulti-axis Synchronous Sliding M ode Control of Integral Separation PID A lgorithm Research

CHENGWen-ya，LUO Liang，LIU Zhi-gui
（School of Manufacturing Science and Engineering，Southwest University of Science and Technology，Mianyang Sichuan 621010，China）

In order to improve the synchronization performance between themultiple axis system，the integral separation PID algorithm is used to solve problems of the traditional coupling synchronization control algorithm gain constant is difficult to determ ine.Multi-axis synchronization error first handled by the integral separation PID then introduced into the slidingmode control of sw itching function.Makes the design of sliding mode control law is not only contain the the system error and also system synchronization error，at the same time in order to ensure that the dynamic performance of the slidingmodemotion，slidingmodemotion using exponential reaching law.On the basis of the principle of Lyaunov stability analysis the asymptotic stability of the algorithm is proved.Finally compared w ith biaxialw ithout coupling compensation system，the design algorithm is verified that it can not only ensure uniaxialmotion performance of the system，but also can effectively enhance themulti-axis synchronization performance.

integral separation PID；coupling compensation；sliding-mode control；multi-axis synchronous

TH165；TG659

A

1001-2265（2015）08-0097-04 DOI：10.13462/j.cnki.mmtamt.2015.08.025

2015-03-10；

2015-04-07

四川省研究生教育改革创新项目"控制工程专业学位硕士研究生教育实践基地建设"（14JGCX01）；西南科技大学控制工程专业学位硕士研究生实践基地建设项目（113-101011）

程文雅（1989-），女，河南禹州人，西南科技大学硕士研究生，研究方向为运动控制器，数控机床多轴运动控制，（E-mail）739626143@ qq.com；刘知贵（1966-），男，四川射洪人，西南科技大学教授，博士生导师，研究方向为控制理论和计算机应用技术；通讯作者：罗亮（1977-），男，湖南耒阳人，西南科技大学讲师，博士，研究方向为嵌入式系统研究与装备控制器研发。