基于小波神经网络的主轴热误差预测研究*

吴文嘉，王 军2，，张辉杰，孙 军

（1.沈阳建筑大学，交通与机械工程学院，沈阳 110168；2.沈阳理工大学，机械工程学院，沈阳110159）

基于小波神经网络的主轴热误差预测研究*

吴文嘉1，王 军2，1，张辉杰1，孙 军1

（1.沈阳建筑大学，交通与机械工程学院，沈阳 110168；2.沈阳理工大学，机械工程学院，沈阳110159）

以TX1600G镗铣加工中心镗削系统主轴部件为研究对象，针对其热误差问题，提出一种基于小波神经网络的预测方法。首先根据镗铣加工中心主轴部件的结构特点建立其有限元模型，基于该模型进行热-结构耦合分析，进而选取热关键点并获取其样本数据；然后利用小波神经网络建立主轴热误差预测模型，并与BP神经网络预测结果相对比；最后结果表明小波神经网络预测精度高，为该加工中心的主轴热误差预测提供了理论依据，该方法同样适用于其它主轴热误差的前期预测。

镗铣加工中心；热-结构耦合；小波神经网络；热误差预测

0 引言

在各种高速、精密机床加工过程中，热变形导致的机床误差问题日益突出，严重影响零件加工精度。主轴是核心的数控机床部件，大量研究表明，由主轴温升导致的热误差是机床的主要误差源。因此，为了保证工件的加工质量，必须采取有效的措施对主轴热误差进行预测并补偿。

热误差模型的建模质量和建模方法将会直接影响到误差预测系统的实施效果，构建一个准确的热误差模型是预测热误差的第一步。大多数的建模方法，都是通过分析热误差和一些热关键点之间温度的变化，寻找最佳的映射关系从而得到热误差模型。例如，神经网络技术通过温度数据的映射关系来预测热误差［1-3］，线性回归分析［4］用来解决热误差模型中多项式的系数。杨建国［5］通过采用投影寻踪多元线性回归的新方法进行热误差分析，从而构建一个稳定的热误差模型。张毅等［6］引用基于灰色理论预处理的人工神经网络（GM-ANN）方法在一台处于实际加工状态的数控车床上进行实验，最终建立热误差模型。实验结果表明，神经网络能够很好的预测误差，可以显著降低零件的尺寸误差。但是人工神经网络较为复杂且容易收敛到局部最优解，线性回归分析得到的预测结果精度又不高。因此，在热误差预测方法中，人们一直通过结合其它理论来形成性能更好的神经网络，例如结合小波理论形成的小波神经网络［7-11］等。

本文在“复杂箱体精密智能复合式锁铣加工中心的研发与开发”和“锁铣加工中心热误差智能化检测与补偿技术研究”课题背景下，以锁铣加工中心锁削系统主轴部件为研究对象，采用有限元方法建立模型，并进行热结构藕合分析，然后采用小波神经网络对选取的热关键点进行热误差预测研究。结果表明，该方法具有一定的普遍意义且可为本加工中心主轴热误差的后续研究奠定理论基础。

1 镗铣加工中心主轴部件有限元分析

1.1 镗铣加工中心主轴部件结构

TX1600G锁铣加工中心采用龙门式铣削结构与卧式锁削结构相结合的结构布局，其主要部件分别为床身、工作台、横梁、铣立柱、铣滑台、锁立柱、锁滑台、主轴箱、滑枕。

TX1600G锁削系统主轴结构，如图1所示。机械主轴由两对角接触球轴承支撑，轴承能承受较大的轴向载荷且允许的极限转速达到6000r/min。

图1 TX1600G镗削系统主轴结构图

1.2 主轴有限元模型建立及参数计算

TX1600G锁铣加工中心锁削系统采用机械式主轴结构，主轴系统主要热源为前、后轴承的摩擦生热，对于主轴系统空转时可不考虑电动机和减速器发热，忽略切削热。影响加工精度的主要因素是主轴的温升变形，所以热分析应围绕着主轴来进行。主轴前后端的两对角接触球轴承有统一的发热公式，故将两对轴承简化成两对发热体，图2为TX1600G锁削系统主轴有限元模型。由式（1）计算得主轴轴承热量Q为［12］

中国戏曲的源流可以追溯到传奇小说，小说与戏曲的沿承关系可以从经典故事的历代改编中考证，如唐传奇《莺莺传》与王实甫《西厢记》等都是后者对前者进行继承发展及再创作的关系，李渔的戏曲理论也是在这样的大环境下提出来的，他将话本归为无声的戏剧，如《十二楼·拂云楼》第四回中说到:“各洗尊眸，看演这出无声戏。”话本即戏剧是李渔拟话本创作的核心。他将戏剧创作的原则以及其他方面的理解都集中注入《闲情偶寄》中，《闲情偶寄》中的曲论，组织周密、条理清楚，形成了我国第一个比较完整的理论批评体系。［3］笔者通过对《无声戏》《十二楼》《闲情偶寄》的仔细研读，总结出李渔戏曲创作理论有以下几点内容:

式中：M为轴承摩擦力矩，N·m；n为轴承转速，r/min。M由M1和M2两部分组成，M1为与轴承载荷、滚动体接触变形及滑动摩擦有关的摩擦力矩分量；M2为与轴承负荷、润滑剂的流体动力消耗、轴承转速有关的摩擦力矩分量。M1和M2分别可由式（2）～（4）计算［13］

若γn≥2000m2·r/min2

若γn＜2000m2·r/min2

式中：f1为与轴承类型和负载有关的系数；p1为确定轴承摩擦力矩的计算负荷，与轴承类型和径向、轴向载荷有关；f2为与轴承结构和润滑方式相关的系数；γ为轴承润滑运动粘度，m2/s；dm为轴承中径，mm。

图2 TX1600G镗削系统主轴有限元模型

主轴材料的物理性能参数如下，其中：材料的弹性模量E=216GPa，热膨胀率α=1.2×10-5m/℃，泊松比ν=0.3，导热系数λ=55W/m·℃，密度ρ= 7850kg/m3，比热容C=462J/kg·℃。

1.3 主轴温度场和热变形分析

热负荷和对流热传递系数可通过上述提到的公式来计算。假定主轴的旋转速度为2000 r/min和空载的条件下，前后轴承所产生的热量分别是102W和85.4W，利用ANSYS得到稳态时的温度场分布和前后轴承及轴头处温升曲线，如图3和图4所示。

图3 主轴稳态时温度场分布

图4 轴承处温升曲线

为了减少主轴头向前的轴向热膨胀，后轴承通常允许主轴在轴向方向上自由地移动，同时前轴承不允许。根据轴承的特性，施加适当的约束到主轴，然后进行热结构藕合分析，图5为主轴藕合分析后的轴向变形图，图6为主轴热变形随时间变化的曲线。

图5 主轴轴向变形图

图6 主轴热变形随时间变化曲线

2 小波神经网络的拓扑结构和设计方法

小波神经网络是把小波变换和BP神经网络有机结合起来的神经网络模型，用小波基函数替代隐含层节点的激励函数，信号向前传播的同时误差能够反向传播。

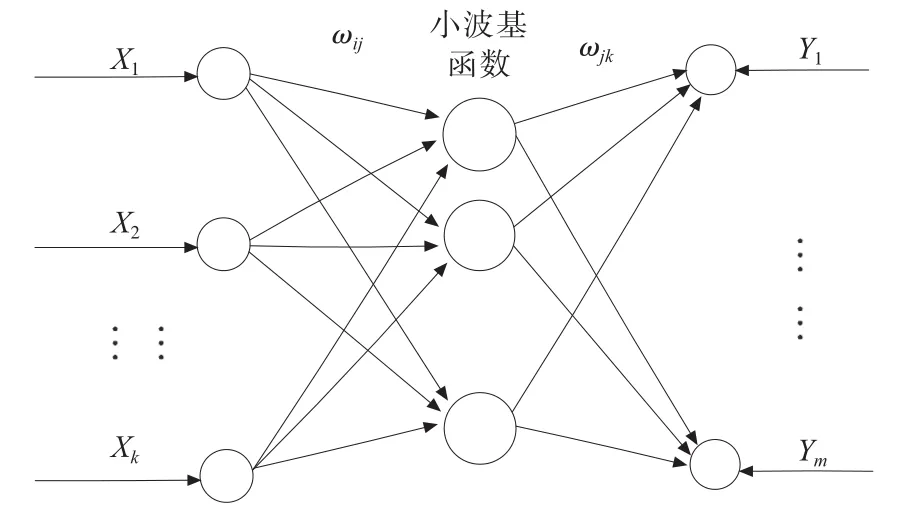
图7 小波神经网络的拓扑结构图

图7中，X1，X2，…，Xk是小波神经网络的输入参数，Y1，Y2，…，Yk是小波神经网络的预测输出，ωij和ωjk为小波神经网络权值。在输入信号序列为Xi（i=1，2，...，k）时，隐含层输出计算公式为

式中，h（j）为隐含层第j个节点输出值；ωij为输入层和隐含层的连接权值；bj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子；hj为小波基函数。小波神经网络输出层计算公式为

式中，ωik为隐含层到输出层权值；h（i）为第i个隐含层节点的输出；l为隐含层节点数；m为输出层节点数。

小波神经网络算法训练步骤如下：

步骤1：网络初始化。随机初始化网络连接权重ωij、ωjk以及小波函数伸缩因子ak、平移因子bk，设置网络学习速率η。

步骤2：样本分类。把样本分为训练样本和测试样本两部分，前者用于训练网络，后者用于测试网络预测精度。

步骤3：预测输出。把训练样本导入网络，得到网络预测输出值，并计算预测输出值和期望输出值的误差e。

步骤4：权值修正。根据误差e修正小波函数参数和网络权值，提高网络预测精度。

步骤5：判断算法是否结束，若没有结束，回到步骤3重新开始。

3 小波神经网络对主轴热误差预测模型设计

3.1 主轴热关键点数据获取

研究表明，数控机床温度场各点的温升对机床热变形的影响程度是不同的，存在这样一些点，它们的温度变化将会引起机床热误差的明显变化，这些点即为热关键点［14］。只有从大量温度测点中辨识出这些热关键点，才能建立合理的热误差模型，补偿机床热变形误差。

本文选取了主轴在2000r/min且空载条件下随时间变化的三个温度敏感点温度值（主轴前轴承处T1，主轴后轴承处T2，主轴头T3）和主轴轴向热变形值S作为热关键点数据。温度传感器单位为：℃，位移传感器单位为：μm。样本数据如表1所示。

表1 主轴热关键点样本数据

3.2 小波神经网络模型的建立

根据表1数据设计小波神经网络，其结构分为输入层、隐含层和输出层三部分。其中，第一层为输入层，包含3个节点，分别对应T1、T2、T3三个输入温度值；隐含层节点可通过经验公式计算得出：

式中：m和n分别为输入层和输出层的节点个数；a的取值范围为［1，10］。所以该神经网络隐含层的神经元个数应为2～12。经过多次测试确定隐含层神经元个数为6；第三层为输出层，表示输出热变形值S。小波神经网络结构为4-6-1。

基于小波神经网络对TX1600G锁削系统主轴热误差预测算法流程如图8所示。

图8 主轴热误差预测算法流程图

4 主轴热误差预测仿真分析

本文将所采集在恒定转速下的200组主轴样本数据分成两部分，具体分组方法为：将所采集恒定转速下的200组样本数据进行编号，一是小波神经网络的测试数据为编号能被4整除的50组样本数据；二是小波神经网络的训练数据为编号不能被4整除的150组样本数据。最后用训练好的小波神经网络预测测试数据。

本论文采用的小波神经网络初始权值为ωij= 0.2506，ωik=1.0446，学习概率lr1=0.01，lr2= 0.001，迭代次数100次。Morlet函数为小波基函数，数学公式为

小波神经网络和标准BP神经网络的建模效果如图9所示。本文采用相对误差百分比评价主轴热误差的预测模型。其建模对比结果如表2。

表2 建模对比结果

图9 建模效果图

预测结果表明，小波神经网络预测模型精度高、收敛过程相对稳定，预测误差始终在0μm上下平稳浮动且最大相对误差百分比仅为0.498%。

5 结论

（1）本文通过有限元方法建立TX1600G锁铣加工中心锁削系统主轴部件的温度场和热变形模型。利用该模型对主轴系统的热特性进行详细分析，初步预测主轴部件的温升和热变形情况，并据此判断主轴的热关键点，为主轴部件进一步的热误差预测奠定基础。

（2）通过探讨基于小波神经网络的热误差预测方法，并将其建模效果与BP神经网络作比较，研究表明小波神经网络所需节点数目少且预测精度高，使本加工中心的主轴热误差达到更好的预测效果，应用前景良好。

本文的研究结果对同类型加工中心的主轴热误差预测及补偿方法的研究也具有极强的指导意义和参考价值。

［1］Haitao Z，Jianguo Y，Jinhua S.Simulation of thermal behavior of a CNC machine tool spindle［J］.International Journal of Machine Tools and Manufacture，2007，47（6）：1003-1010.

［2］Li Z，Yang J，Fan K，et al.Integrated geometric and thermal error modeling and compensation for vertical machining centers［J］.The International Journalof Advanced Manufacturing Technology，2015，76（5-8）：1139-1150.

［3］Zhang Y，Yang J，Jiang H.Machine tool thermal errormodeling and prediction by grey neural network［J］.The International Journal of Advanced Manufacturing Technology，2012，59（9-12）：1065-1072.

［4］Lee JH，Yang SH.Statistical optimization and assessment of a thermal errormodel for CNCmachine tools［J］.International Journal of Machine Tools and Manufacture，2002，42（1）：147-155.

［5］Qianjian G，Jianguo Y.Application of projection pursuit regression to thermal error modeling of a CNC machine tool［J］.The International Journal of Advanced Manufacturing Technology，2011，55（5-8）：623-629.

［6］张毅，杨建国.基于灰色理论预处理的神经网络机床热误差建模［J］.机械工程学报，2011，47（7）：134-139.

［7］王健，孙结松.BP与小波神经网络短时交通流预测对比研究［J］.科技视界，2014（24）：73-74.

［8］黄伟，何晔，夏晖.基于小波神经网络的IP网络流量预测［J］.计算机科学，2011，38（B10）：296-298.

［9］Chen Y，Yang B，Dong J.Time-series prediction using a local linear wavelet neural network［J］.Neurocomputing，2006，69（4）：449-465.

［10］Zainuddin Z，Pauline O.Modified wavelet neural network in function approximation and its application in prediction of time-series pollution data［J］.Applied Soft Computing，2011，11（8）：4866-4874.

［11］Wei S，Yang H，Song J，et al.A wavelet-neural network hybrid modelling approach for estimating and predicting river monthly flows［J］.Hydrological Sciences Journal，2013，58（2）：374-389.

［12］叶伯生，杨叔子.CNC系统中三次B-样条曲线的高速插补方法研究［J］.中国机械工程，1998，9（3）：42-43.

［13］高钟毓.机电控制工程［M］.北京：清华大学出版社有限公司，2002.

［14］赵瑞月，梁睿君，叶文华.基于模糊聚类与偏相关分析的机床温度测点优化［J］.机械科学与技术，2012，31（11）：1767-1771.

（编辑 赵蓉）

Spindle Thermal Error Prediction Based on W avelet Neural Network

WUWen-jia1，WANG Jun2，1，ZHANG Hui-jie1，SUN Jun1
（1.Traffic and Mechanical Engineering School，Shenyang Jianzhu University，Shenyang 110168，China；2.Mechanical Engineering School，Shenyang Ligong University，Shenyang 110159，China）

Taking the boring spindle system of TX1600G boring-m illingmachining center as the research object，awaveletneuralnetwork-based predictionmethod is proposed to solve the thermalerror problem.Firstly a finite elementmodel of the spindle is established according to the structural characteristics of the boringmilling machining center，thus the thermal key points are selected and the sample data are obtained after the thermal-structure coupling analysis is processed based on the model above；secondly，w ith the method of wavelet neural network，the prediction model of spindle thermal error is built up，which compared w ith the prediction results of BP neuralnetwork；finally，the results indicate that the prediction based on waveletneural network is of higher precision，which provides a theory evidence for the thermal error prediction of the machining center spindle and thismethod is also applicable to what predicts the spindle error of other types.

boring-milling machining center；thermal-structure coupling；wavelet neural network；thermal error prediction

TH161；TG536

A

1001-2265（2015）08-0093-04 DOI：10.13462/j.cnki.mmtamt.2015.08.024

2015-03-11

国家863计划重大项目（2012AA041303）；辽宁省科技计划项目（2013220017）

吴文嘉（1991-），女，辽宁朝阳人，沈阳建筑大学硕士研究生，研究方向为数字化设计制造与应用，（E-mail）15804092375@163.com；王军（1956-），男，辽宁丹东人，沈阳理工大学、沈阳建筑大学教授，博士生导师，研究方向为先进制造技术。