基于MATLAB的研磨喷射装置优化设计

刘晓初，何铨鹏，龚伟威，谈世松，郭莹莹，王 豪

（1.广州大学a.机械与电气工程学院；b.金属材料强化研磨高性能加工重点实验室，广州 510006；2.佛山职业技术学院，广东佛山 528000）

基于MATLAB的研磨喷射装置优化设计

刘晓初1a，1b，何铨鹏1a，1b，龚伟威1a，1b，谈世松1a，1b，郭莹莹1a，王 豪1b，2

（1.广州大学a.机械与电气工程学院；b.金属材料强化研磨高性能加工重点实验室，广州 510006；2.佛山职业技术学院，广东佛山 528000）

为了提高研磨喷射装置的稳定性，在研究强化研磨系统工作原理和装置结构的基础上，通过5 -why分析法推断出该装置左右移动时产生振动的原因，并结合实际情况建立了导杆受力模型。此外，通过Matlab计算出优化设计前导杆挠度的最大值，验证了因导杆弯曲变形过大而使螺杆受力的推论，并根据导杆最大挠度与横截面直径关系来确定导杆的最优直径。

强化研磨；喷射装置；优化设计；导杆

0 引言

在轴承生产中，内圈（以下简称工件）的加工一般需经切削、磨削等6道工序。强化研磨作为提高工件滚道表面性能的后续工序，是一种基于复合加工方法的抗疲劳、抗腐蚀、抗磨损金属材料精密加工技术［1-2］。为了提高强化研磨样机加工效率，对其进行了包括上下料、研磨喷射，电磁无心装夹和废气过滤等装置的自动化设计。其中，丝杠滑台是研磨喷射装置的主要机构，由直线步进电机控制其螺杆，使滑台左右与前后移动，以达到调整高压喷头与工件位置的目的。

然而，自动化设计后的研磨喷射装置在左右移动时不稳定，经常产生振动，不但直接影响工件加工效率和质量，而且容易损坏电机。因此，针对现有研磨喷射装置的不足，运用企业管理中“5-why”分析法追究其根本原因，再利用Matlab进行优化设计，从而提高该装置的稳定性。

1 系统工作原理

强化研磨系统的工作原理如图1所示，工件通过电磁无心夹具与左右支承共同作用的方法固定，并在异步电机带动下高速旋转；加工前，高压喷头向右前方移动，与工件保持合适的距离；加工时，工件表面不仅因高强度钢球冲击而产生弹塑性变形和亚晶粒细化，形成强化层，且因研磨粉微切削以及研磨液悬浮、冷却、清洗和润滑等一系列固液两相流场变化的作用而获得较小的表面粗糙度，达到对工件表面强化研磨的效果［3］；加工后，高压喷头向左后方移动，防止与上下料装置产生干涉。

2 研磨喷射装置故障分析

2.1 研磨喷射装置结构

自动化设计后的研磨喷射装置由两个以十字形式安装的丝杠滑台，高压喷头和支架组成。一方面，支架安装高压喷头后与第一根螺杆（以下简称螺杆1）上的滑台相联接，实现前后方向移动；另一方面，螺杆1的丝杠滑台底座与第二根螺杆（以下简称螺杆2）上的滑台相联接，实现左右方向移动。其中，丝杠滑台以螺杆作为传动元件，由直线步进电机通过联轴器带动，两侧导杆主要起导向和承受径向载荷作用，结构如图2所示：

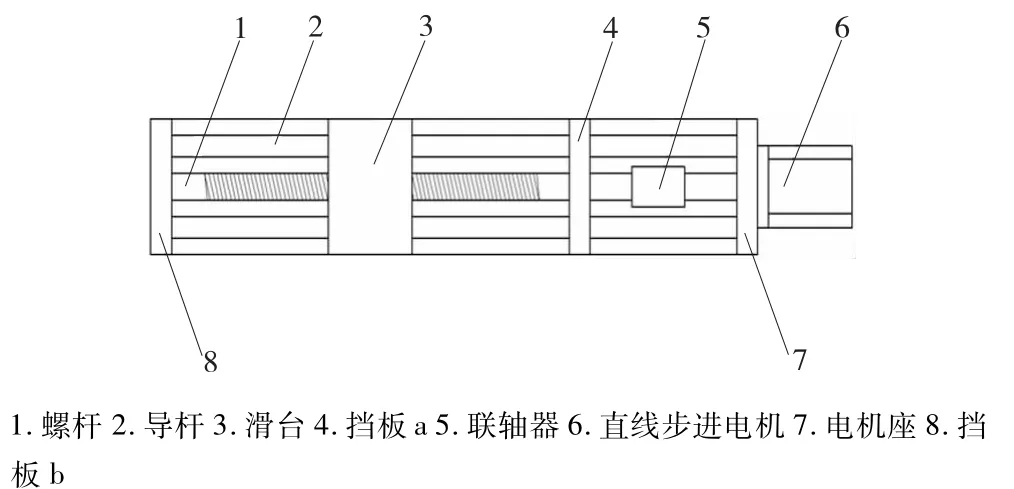
图2 丝杠滑台结构

2.2 5-why分析法故障分析

经过一段时间运行后，研磨喷射装置在左右移动时容易产生振动，严重影响工件加工质量和效率。因此，以“为什么研磨喷射装置左右移动时不稳定”为出发点，利用企业管理中5-why分析法列举各种影响因素，并沿着因果关系链逐步排除主观假设，从问题的本质上寻找解决方法。5-why分析结果如表1所示。

螺杆承受径向载荷是设计禁忌，应让该载荷集中到两侧导杆上［4-6］。从表1可知，导杆产生弯曲变形后，螺杆承受了因装置自重而产生的部分径向载荷，当螺杆2的滑台移动至导杆弯曲段时，装置容易产生振动［7］。

工程中一般以挠度反映受弯构件在径向荷载作用下的变形程度。因此，解决上述问题的根本方法在于研究螺杆2两侧导杆的挠度、横截面直径和径向载荷三者之间的关系。

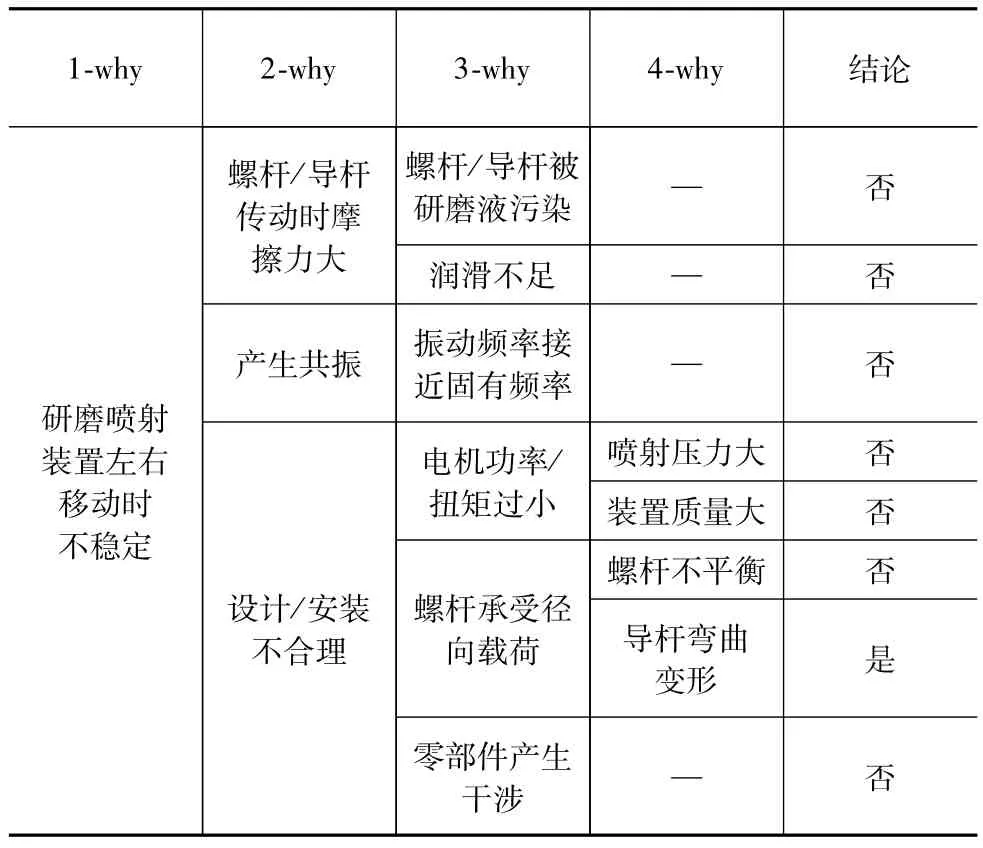
表1 5-why分析

3 导杆优化设计

3.1 导杆受力模型的建立

由于研磨喷射装置需倒置安装，定位螺栓与丝杠滑台底座、两侧挡板底端相接，且丝杠滑台中的导杆末端与电机座相连，直线步进电机全部质量集中在电机座上，所以将导杆视为外伸梁更为合理［8-10］。导杆受力模型如图3所示，挡板a和挡板b之间的导杆为简支梁AD，且其与滑台配合部分承受径向动载荷F2；挡板a与电机座之间的导杆为悬臂梁DE，且其末端承E受径向载荷F1。

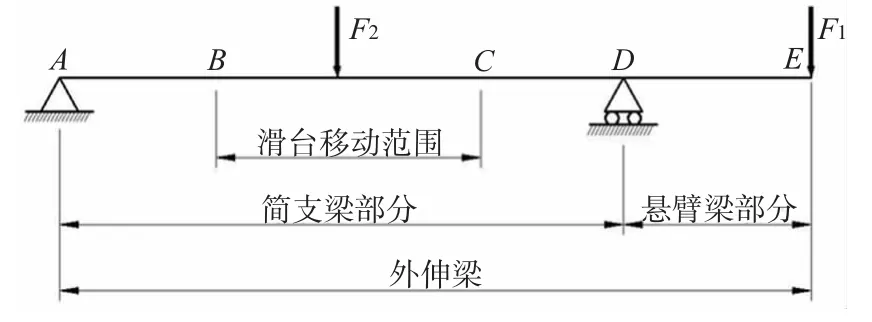
图3 导杆受力模型

3.2 导杆的挠度

如图4所示，设悬臂梁上的点到D距离为x1，DE长度为L1，梁上载荷为F1。

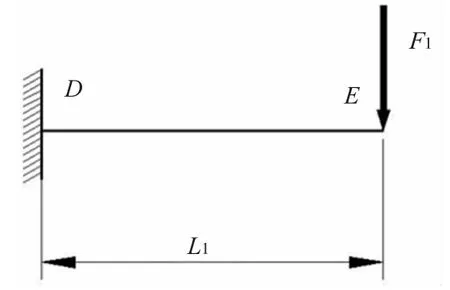
图4 悬臂梁部分

如图5所示，设简支梁上的点到A距离为x2，动载荷F2到A的距离为a，到D点的距离为b，AD长度为L2。除动载荷F2外，截面D上还受剪切力Fs和弯矩M，且Fs=F1，M=F1×L1。

图5 简支梁部分

3.2.1 悬臂梁部分的挠度

3.2.3 导杆挠度分析

由式（6）、（9）可知，当导杆长度和受力大小确定后，挠度γ与变量x、动载荷位置a、导杆截面惯性矩I有关。其中，I的计算公式为：

式中 d-导杆截面直径，mm

3.3 基于M atlab的最大挠度计算

优化设计前，导杆材质为45钢，直径d=16mm，则I=3217mm4，弹性模量E=2.1×105MPa；外伸梁AE为350mm，其中悬臂梁部分 L1=100mm，x1∈［0，100］，简支梁部分L2=250mm，x2∈［0，250］，b=250-a；根据受力分析，若安全系数S=1.5，则径向载荷F2=8F1≈200N，M=2500N·mm；AB为50mm，滑台在导杆上的移动范围BC为120mm，因滑台宽度为60mm，所以动载荷F2的实际作用距离为±30mm，即a∈［80，140］。

将上述数据代入式（6）和（9）分别得出挠度计算方程（11）、（12）、（13）。

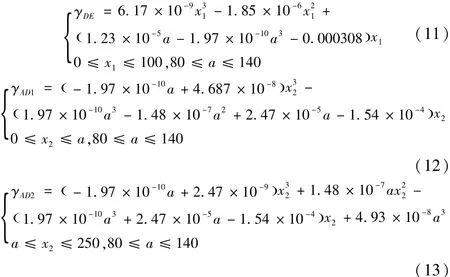
通过Matlab可求出目标方程的最大/最小值，并绘制出方程的三维曲面图［11-13］。

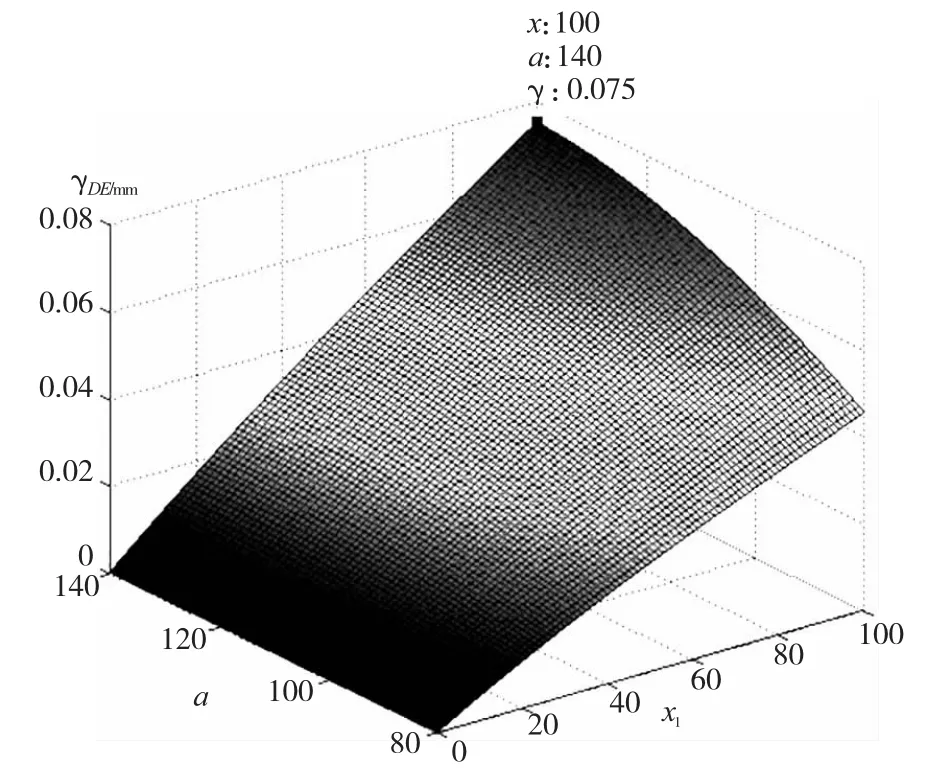
图6 目标方程11三维曲面图

由计算可知，当x1=100，a=140时，悬臂梁部分挠度最大，γDEmax=0.07501mm，对应图6中的最高

点。

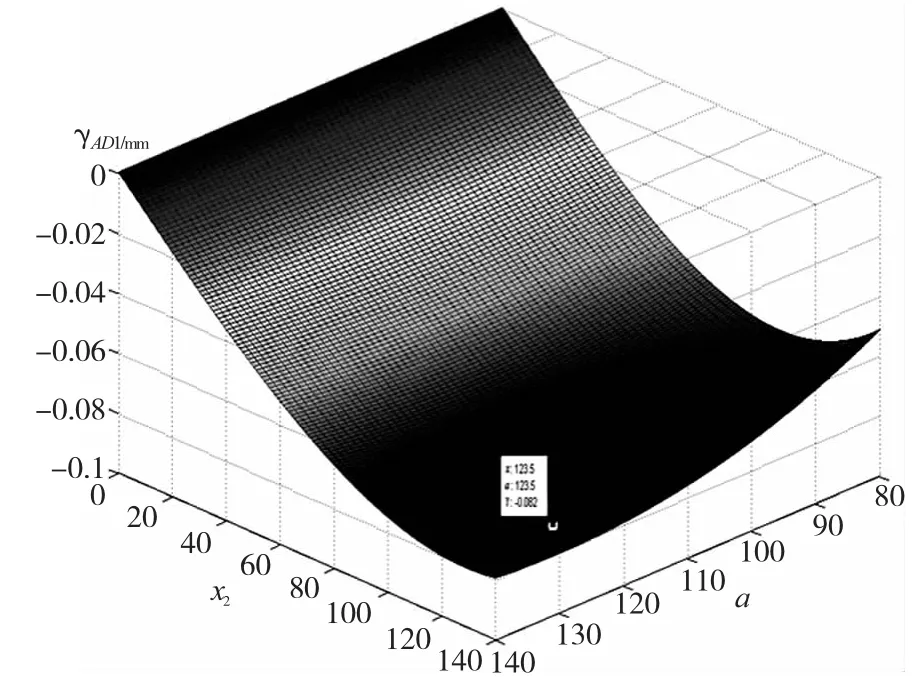
图7 目标方程12三维曲面图

由计算可知，在x2≤a条件下，当x2=123.5， a=123.5时，简支梁F2左侧挠度最大，= 0.08235mm，对应图7中的最低点。

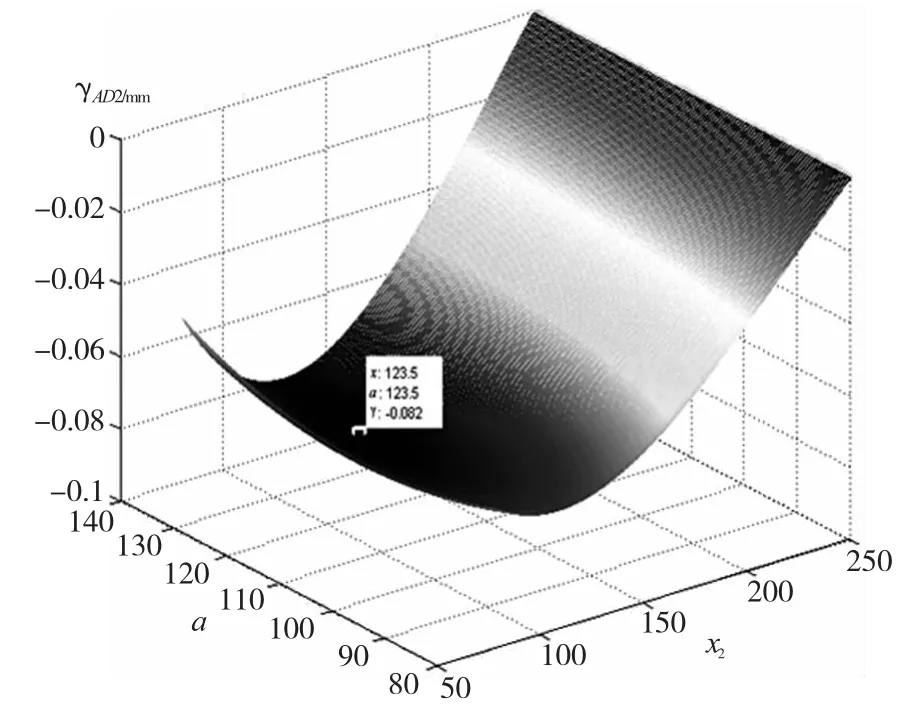
图8 目标方程13三维曲面图

由计算可知，在a≤x2条件下，当x2=123.5， a=123.5时，简支梁F2右侧挠度最大，= 0.08238mm，对应图8中的最低点。

3.4 导杆最优直径的确定

联合式（10），并将x2=123.5，a=123.5代入式（9）的任一计算方程中，得出导杆最大挠度与横截面直径的关系式

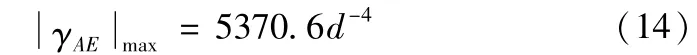
如图9所示，当d≥16.65mm时，丝杠滑台的导杆满足设计要求。

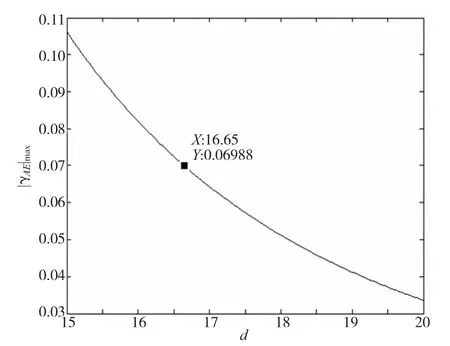
图9 导杆最大挠度与横截面直径关系

4 结束语

（1）简述强化研磨系统工作原理，并根据研磨喷射装置结构，利用5-why分析法得出该装置产生振动的原因是导杆弯曲变形；

（2）结合实际，建立了导杆受力模型，并利用Matlab计算出优化设计前导杆最大挠度为0.082mm，大于许用挠度［］γ=0.07mm，从而验证了因导杆弯曲变形过大使螺杆受力的推论；

（3）在计算导杆最大挠度的基础上，推导出当x2=123.5，a=123.5时，导杆最大挠度与横截面直径d的关系式，并得出了导杆直径d≥16.65mm时满足设计要求的结论。

［1］刘传剑，刘晓初，李文雄，等.轴承套圈沟道强化研磨加工中碰撞数值模拟分析［J］.轴承，2010（12）：21-24.

［2］刘晓初，黄骏，肖苏华，等.喷射时间对GCr15钢轴承套圈表面粗糙度的影响［J］.金属热处理，2014，39（7）：81-84.

［3］刘晓初，陈志斌，何铨鹏，等.强化研磨加工的仿真及试验［J］.轴承，2014（7）：35-37.

［4］濮良贵，纪名刚.机械设计［M］.北京：高等教育出版社，2006.

［5］吴宗泽，罗圣国.机械设计课程设计手册［M］.北京：高等教育出版社，2009.

［6］吴宗泽.机械设计禁忌1000例［M］.3版.北京：机械工业出版社，2011.

［7］林世袍.变截面钢管杆的挠度计算探析［J］.特种结构，2012，29（6）：26-29.

［8］刘鸿文.材料力学Ⅰ［M］.4版.北京：高等教育出版社，2004.

［9］邓训，徐元杰.材料力学［M］.湖北：武汉大学出版社，2002.

［10］刘衍，汪劲松，赵彤，等.滚珠丝杠传动系统的刚度模型［J］.清华大学学报（自然科学学报），2011，51（5）：601-606.

［11］陈杰.MATLAB宝典［M］.4版.北京：电子工业出版社，2013.

［12］赵继俊.优化技术与MATLAB［M］.北京：机械工业出版社，2011.

［13］王海宾，崔建昆.基于Matlab的齿轮泵的优化设计［J］.机械传动，2014，38（7）：93-96.

（编辑 赵蓉）

Optim ization Design of Abrasive Injection Device Based on MATLAB

LIU Xiao-chu1a，1b，HE Quan-peng1a，1b，GONGWei-wei1a，1b，TAN Shi-song1a，1b，GUO Ying-ying1a，WANG Hao1b，2
（1 a.School of Mechanical and Electrical Engineering；b.Key Laboratory of High-performance Metal Materials Reinforced Grinding Machining，Guangzhou University，Guangzhou 510006，China；2.Foshan Polytechnic，Foshan Guangdong 528000，China）

In order to improve the stability of abrasive injection devicewhen itmoves leftand right，the cause of vibration，based on researches on working principle of reinforced grinding system and structure of abrasive injection device，is deduced through themethod of 5-why analysis.Besides，the forcemodel of guide rod is established combined w ith the actual.In addition，themaximum deflection of guide rod in original design is calculated by Matlab and consequently the inference，screw bears force because of the excessive bending deformation of guide rod，is verified.The optimal diameter of guide rod is determ ined by the relationship between maximum deflection and cross sectional diameter of guide rod.

reinforced grinding；injection device；optim ization design；guide rod

TH123.1；TG65

A

1001-2265（2015）08-0059-04 DOI：10.13462/j.cnki.mmtamt.2015.08.015

2015-03-01

广州市科技计划项目（穗科信字［2013］163-19）；国家科技支撑计划子项目（2011BAF09B01）；广东省教育部产学研结合项目（2012B091000069）

刘晓初（1964-），男，湖南耒阳人，广州大学教授，博士，研究方向为智能装备及机器人、绿色设计与制造，（E-mail）gdliuxiaochu@163. com。