Nonlinear Resonance of the Rotating Circular Plate under Static Loads in Magnetic Field

HU Yuda* and WANG Tong

Hebei Provincial Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures，Yanshan University， Qinhuangdao 066004， China



Nonlinear Resonance of the Rotating Circular Plate under Static Loads in Magnetic Field

HU Yuda* and WANG Tong

Hebei Provincial Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures，Yanshan University， Qinhuangdao 066004， China

The rotating circular plate is widely used in mechanical engineering， meanwhile the plates are often in the electromagnetic field in modern industry with complex loads. In order to study the resonance of a rotating circular plate under static loads in magnetic field， the nonlinear vibration equation about the spinning circular plate is derived according to Hamilton principle. The algebraic expression of the initial deflection and the magneto elastic forced disturbance differential equation are obtained through the application of Galerkin integral method. By mean of modified Multiple scale method， the strongly nonlinear amplitude-frequency response equation in steady state is established. The amplitude frequency characteristic curve and the relationship curve of amplitude changing with the static loads and the excitation force of the plate are obtained according to the numerical calculation. The influence of magnetic induction intensity， the speed of rotation and the static loads on the amplitude and the nonlinear characteristics of the spinning plate are analyzed. The proposed research provides the theory reference for the research of nonlinear resonance of rotating plates in engineering.

circular plate， main resonance， magnetic filed， static load， modified multiple scale method

1 Introduction*

Plates have widespread applications in many fields. With the development of science and technology， rotating plates and electromagnetic structures have been more and more widely used in different fields of industry. The rotating velocity in some instances may has significant influence on the work of rotating plates［1］. Therefore， it is important to analyze the response of the plates.

ALIJANI， et al［2］， investigated the nonlinear vibration of the completely free sandwich rectangular plates subjected to harmonic excitation according to the experiments. And the nonlinear frequency response curves were obtained. The functionally graded plates with multiple circular and non-circular cutouts was analyzed by finite element method［3］. The nonlinear vibration and dynamic response of functionally graded material plates in thermal environments were researched based on general von Karman-type equation［4］， and then， ALLAHVERDIZADEH， et al［5］，developed a semi-analytical approach for nonlinear free and forced axisymmetric vibration research of a thin circular functionally graded plate. The large amplitude free vibration of corrugated circular plates with shallow sinusoidal corrugations was investigated［6］. The plate was subjected to uniformly static temperature changes. It is found that the rise in temperature will decrease the frequency and vice versa. RANJAN， et al［7］， analyzed the determination of the fundamental frequency of vibration of solid and annular circular plate using finite element analysis（FEA）. The plate was with different boundary conditions. and with point mass attached at an arbitrary position. Natural frequencies of a cylindrical gas cavity axially bounded at one end by a liquid interface and a thin elastic disc at the other end were calculated［8］. The hydro elastic vibration of two identical circular plates coupled with a bounded fluid was investigated based on the finite Fourier-Bessel series expansion and the Rayleigh-Ritz method［9］. There are also some researchers who have studied the vibration of circular plates with spinning velocity. HASHEMI， et al［10］， developed a finite element formulation for vibration analysis of rotating thick plates by applying Mindlin plate theory combined with second order strain-displacement assumptions and employing Kane dynamic method. MARETIC［11］investigated a thin circular plate rotating at constant angular speed around the axis perpendicular to the plane of the plate. The stresses and displacements in the plate's middle plane and the natural frequencies of the transverse vibration are determined. The transverse vibration of the circular plate was researched using the method of multiple scales［12］. The plate rotated with constant angular velocity which was clamped at the center and free at the periphery. BAUER， et al［13］，determined the lower approximate natural frequencies of a spinning circular plate with different boundary conditions rotating with constant speed of spin. Some researchers have paid much attention to the vibration of the plates under static loads. DU， et al［14-15］， analyzed the vibration of circular sandwich plate under uniformed load and obtained the amplitude frequency-load character relation of circular sandwich plate. YUAN， et al［16］， investigated the nonlinear forced vibration of a corrugated shallow shell under uniform load based on the large deflection dynamic equations of axisymmetric and obtained the amplitudefrequency response under harmonic force.

On the other hand， magneto-elastic structures were also paid attention gradually. An analytical solution was given for a conductive circular plate in a time-dependent magnetic field by using a T-method of the eddy current［17］. HU， et al［18-20］， studied the resonances of conducting thin plates in magnetic field or functionally graded plates and analyzed the influences of some parameters such as the electro-magnetic on the vibration of the plates. With the development of the research， the strongly nonlinear vibration has been analyzed in recent years. The stability of strongly nonlinear normal modes in multidegree of freedom systems were investigated by standard procedures［21］.

This paper deals with the nonlinear resonance of a conductive rotating thin circular plate under uniform static loads subjected to mechanical loads in magnetic field. By mean of modified Multiple scale method， the strongly nonlinear amplitude-frequency response equation in steady state is established. According to numerical analysis， the influences of different parameters on the amplitude and the nonlinear characteristics of the spinning plate are analyzed.

2 Magneto Elastic Vibration Equations

Consider the circular plate spinning at the speed of Ω in the magnetic field B0zwhich is subjected to the uniform static load Q and periodic excitationPz. The thickness of the plate is h， the radius is R， the modulus of elasticity is E， the passion ratio is μ and the mass density is ρ（see Fig. 1）.

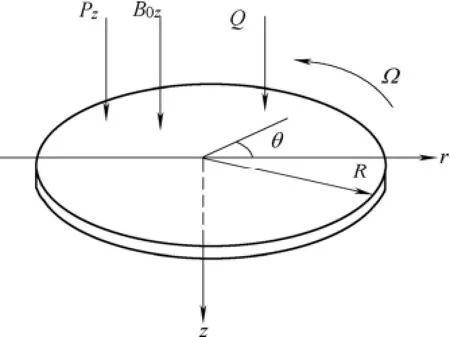
Fig. 1 Mechanical model of the rotating circular plate

The displacement vector at any point in the plate in three directions in cylindrical coordinates （r， θ， z） was assumed as follows:

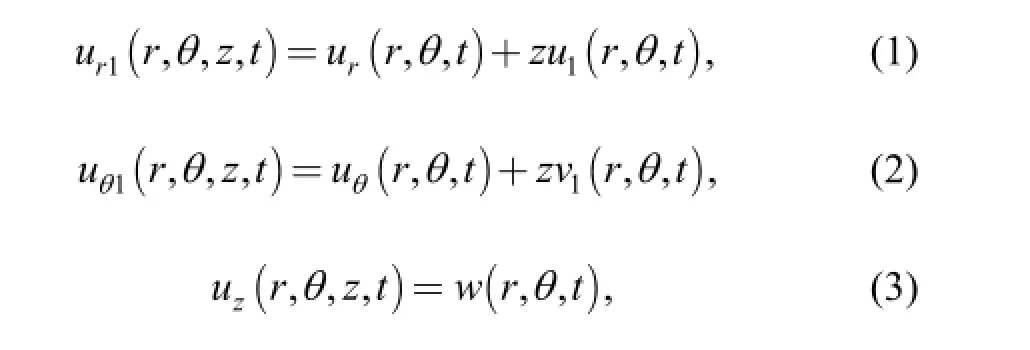
where ur， uθis the displacement in the middle plane， w is the transverse displacement，

are angular displacements， r， θ， z， respectively is radial，circumferential and normal coordinates， t is the time variable.

The expression of the kinetic energy of the rotating plate can be obtained:

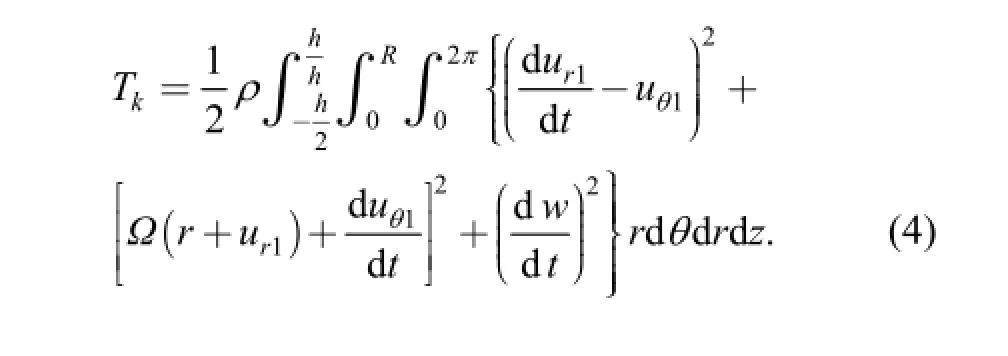
The deformation potential Uε1caused by bending deformation can be given by

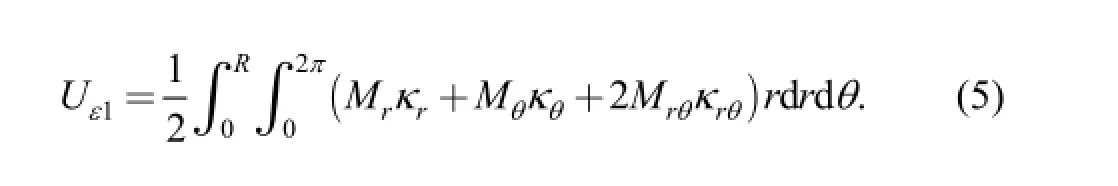
The potential energy of strain in the middle plane of the plate can be expressed by

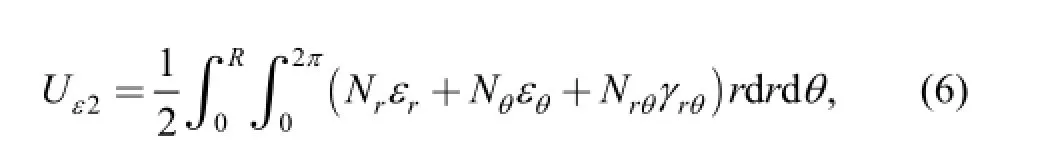
where Mr， Mθare bending moments， Mrθis torque， κr， κθ，are curvatures， κrθis torsion， Nr， Nθ， Nrθare inertial forces in the middle plane， εr， εθ， εrθ， are strains in the middle plane.

It is assumed that the transverse displacement w has occurrence of tiny change which is allowed by the displacement boundary condition， that is， the virtual displacementδw. So the virtual work of the static load Q and the periodic transverse forcezP subjected to the virtual displacement can be written as

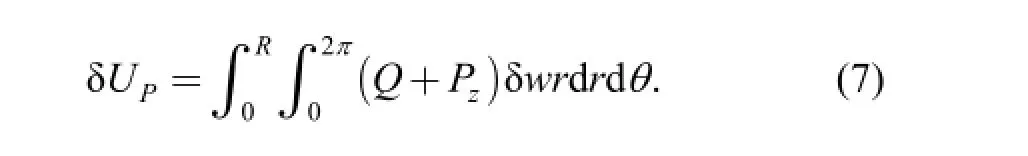
Based on Eqs. （4）-（7）， considering geometric nonlinear condition and symmetric vibration problem， using the Hamilton principle and neglecting the effect of the longitudinal displacement on the lateral vibration of the plate（ur=0， uθ=0）， the magneto elasticity symmetricvibration equation only about the deflection w can be obtained as follows:

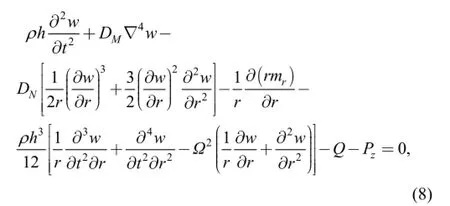
where

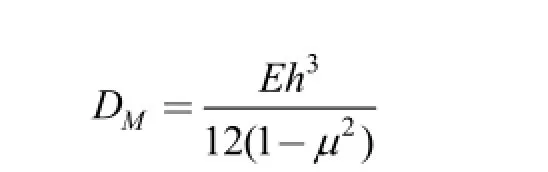
is the flexural rigidity，

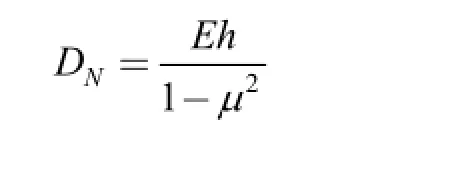
is the tensile rigidity， E is the modulus of elasticity， μ is the Poisson coefficient，is the amplitude of the excitation， ω is the frequency） is the transverse excitation and the electromagnetic torque［22］:

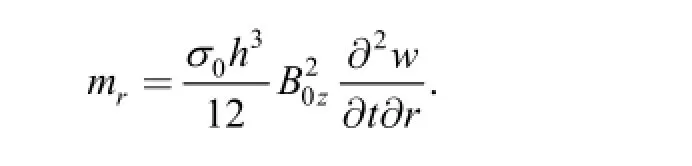
3 Disturbance Deferential Equation

It is assumed that the circular plate has a tiny static deflection w0under the static load Q and its deflection is w1when it vibrates. So the total deflection can be written as

Then Eq. （8） can be rewritten as

The initial deflection satisfies the equation

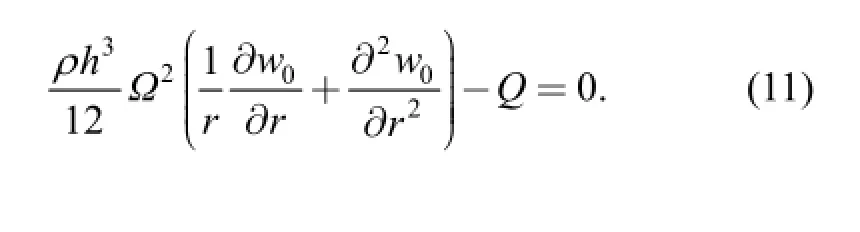
Eq. （11） can be solved by using the Galekin method. We assumed［22］

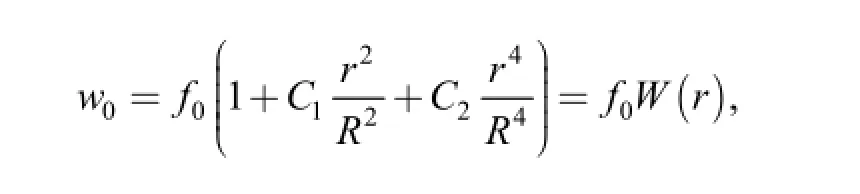
and then substituted w0into Eq. （11） and integrated

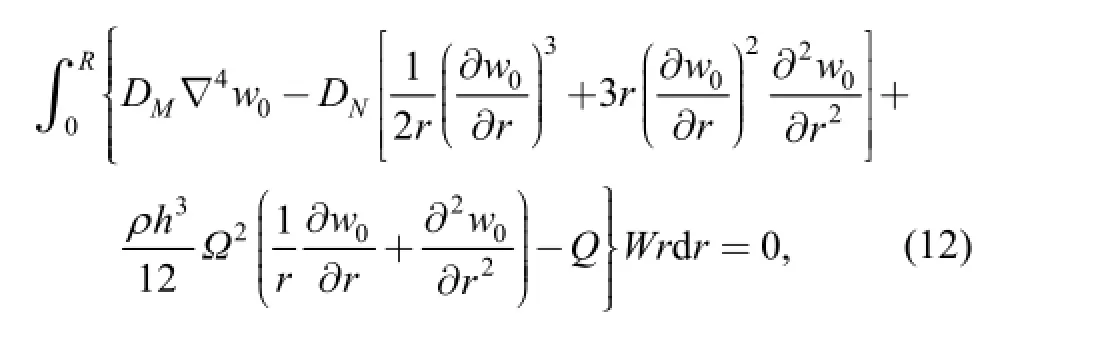
we can obtain

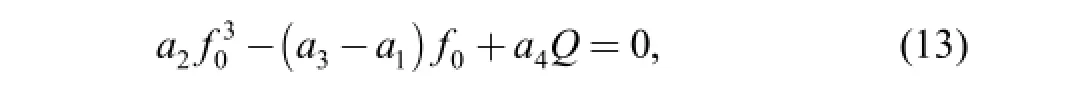
Therefore， we obtained

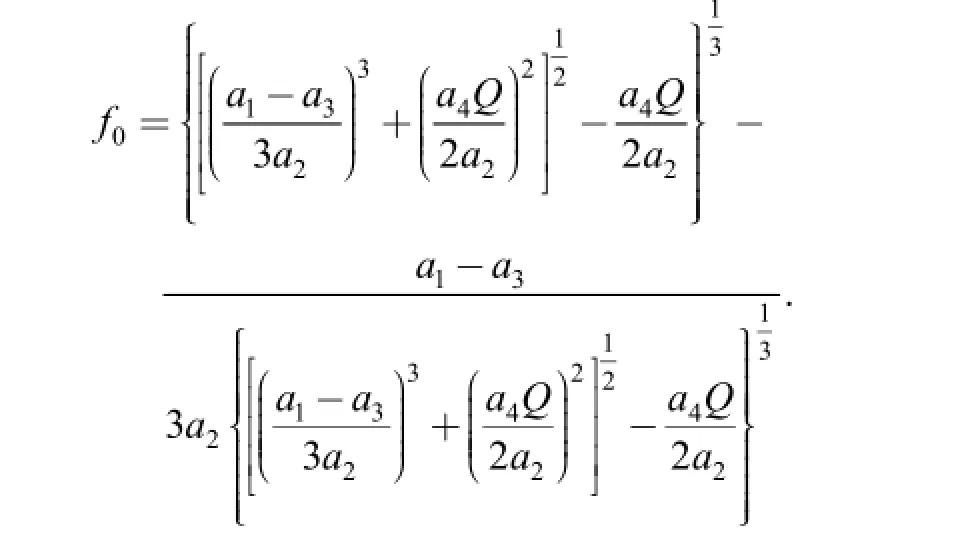
We assumed that the additional deflection1wcan be written as follows:

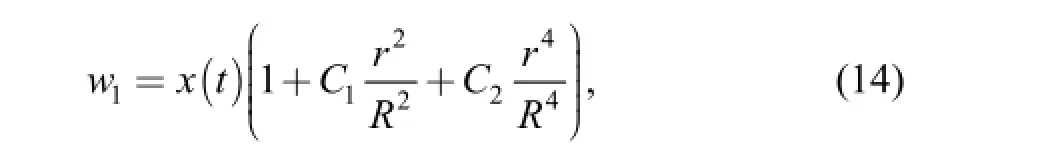
where R is the radius of the plate. The coefficients［23］are

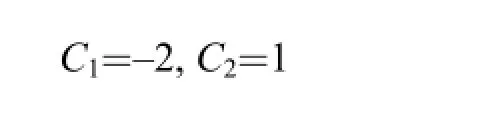
with fixed supported side，with simply supported side.

Substituting Eqs. （11）， （14） into Eq. （10） and using the Galerkin method， we derived the vibration differential equation as follows:

Eq. （15） can be rewritten as

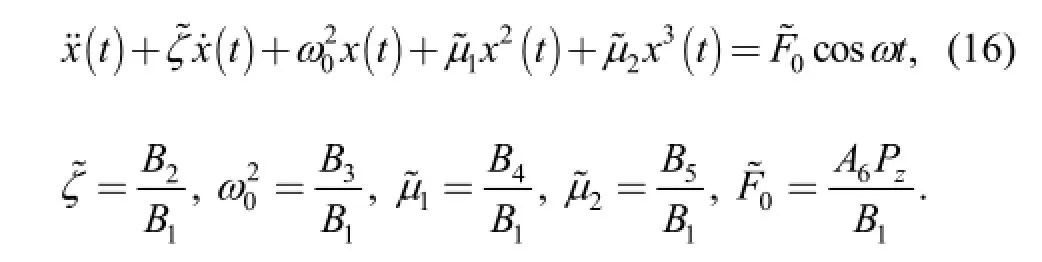
4 Modified Multiple Scales Method for Solution

In order to research the main resonance characteristics of the system， we analyzed the strongly nonlinear problem by using modified multiscale method. Introducing a small parameterε， Eq. （16） can be written in the form of

In order to solve the strong nonlinear problem， the transition was introduced as follows:

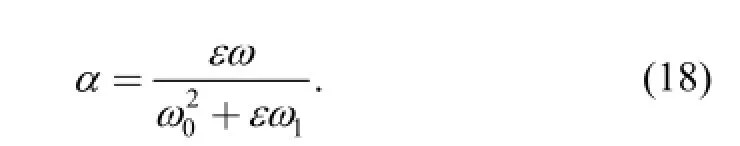
So we got

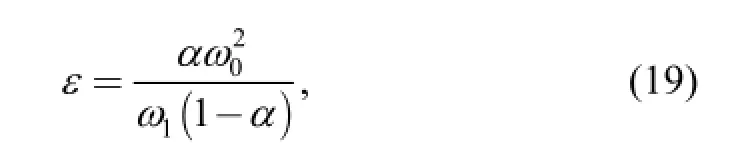
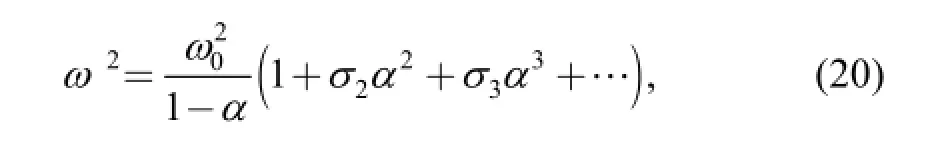
（ω， σjare the undetermined coefficients）or

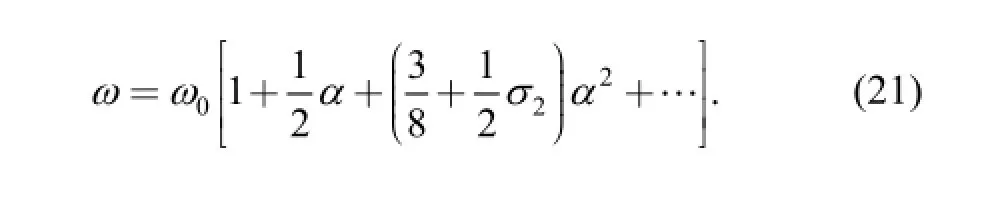
After transition， the strongly nonlinear system about the larger parameter ε has been transformed into the weak nonlinear system about the small parameter α. So， we can solve the problem by General Multi Scale method.

The general solution of Eq.（17） was assumed as follows:

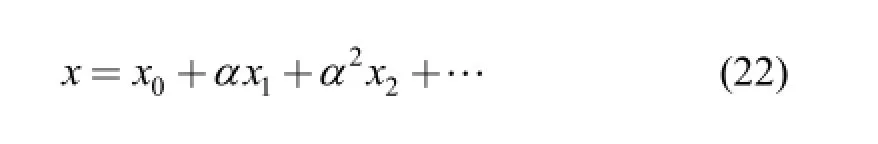
Substituting Eqs. （19）， （20） into Eq. （17）， we can get

After the transition， the strong nonlinear system about ε can be changed to the weak nonlinear system. So we can solve the problem using the general method of Multiple Scales.

The first-order approximate solution of Eq. （23） can be written as

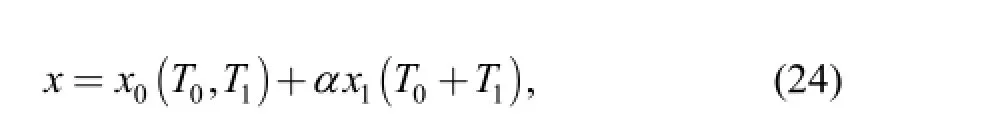
where T0=t， T1=αt.

Substituting Eqs. （22）-（24） into Eq. （23） and equating the coefficients of0α and1α on both sides， we obtained

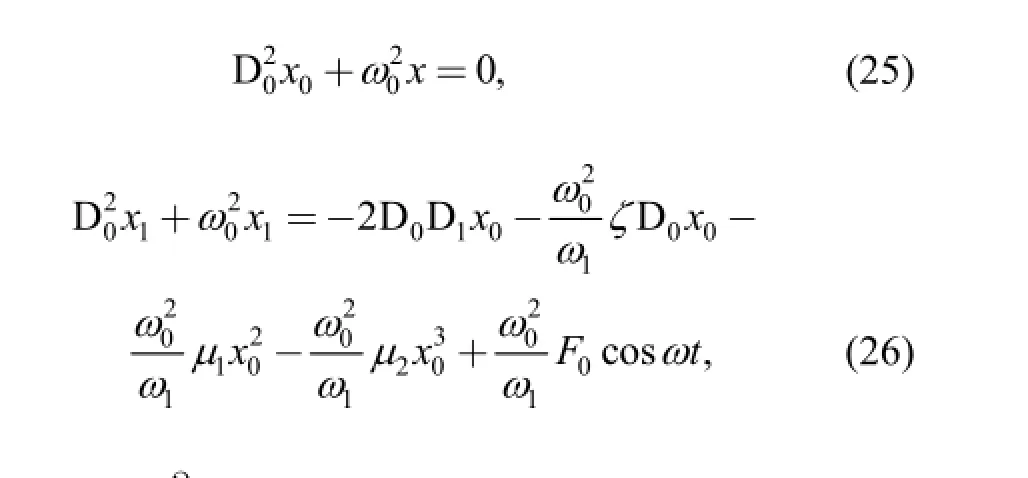
The general solution of Eq. （25） can be written in the form

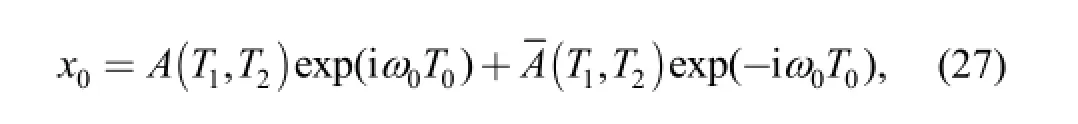
where i2=-1， A is unknown at this stage of the analysis，is the complex conjugate of A.

Substituting Eq. （27） into Eq. （26） and eliminating the secular term， we can obtain

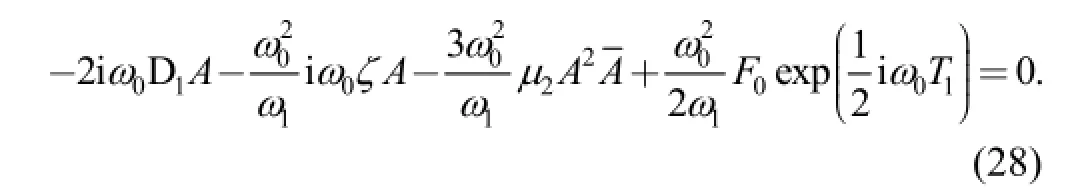
We wroteAin the polar form

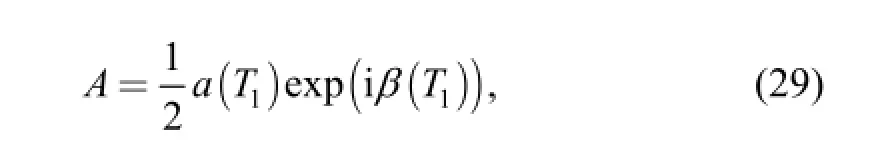
where α and β are real.

Substituting Eq. （29） into Eq. （28），we separated the equation into its real and imaginary parts and obtained

For the steady state motion of the system， we letand then eliminate γ according to Eq. （30）， so we can obtain the amplitude frequency equation:

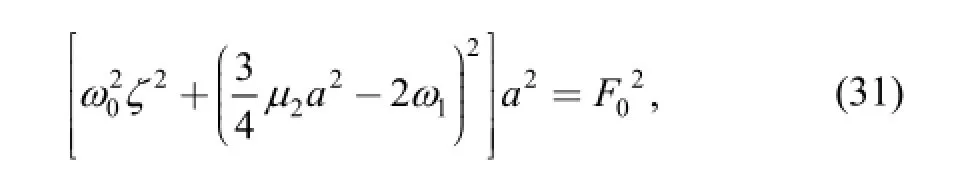
5 Analysis of Numerical Result

The rotating circular thin plate under the static load is made of aluminum. The material properties of the plate used in the present study are: mass density ρ=2670 kg/m3，Young's modulus E=71 GPa and Poisson's ratio μ=0.34.

Fig. 2 shows the curves of the amplitude changing with the tuning parameter. In Fig. 2（a）， 2（b）， 2（c）， R=0.3 m，h=0.004 m， and in Fig. 2（d）， R=0.6 m， h=0.008 m. In Fig. 2（a）， the curve exhibits a single solution when α≤0 and it has multiple solutions with the increase of α. As the magnetic induction intensity increases， the resonance region shows obvious retraction phenomenon and the amplitude decreases as the magnetic induction intensity increases. In Fig. 2（b）， the curve shows that the resonance region retracts obviously and exhibits multiple solutions. At the same time， the curve retracts obviously as the excitation force reduces. Fig. 2（c） and Fig. 2（d） represent the response curves of the amplitude-frequency with different static loads and spinning velocities respectively. In the resonance region， the amplitude increases obviously and has multiple solutions. We also note that there exist multiple points of intersection between the corresponding curves with different static loads or spinning velocities. So we can conclude that there are both increased area and decreased area for the resonance amplitude with the increase of static loads or the decrease of the spinning velocity.

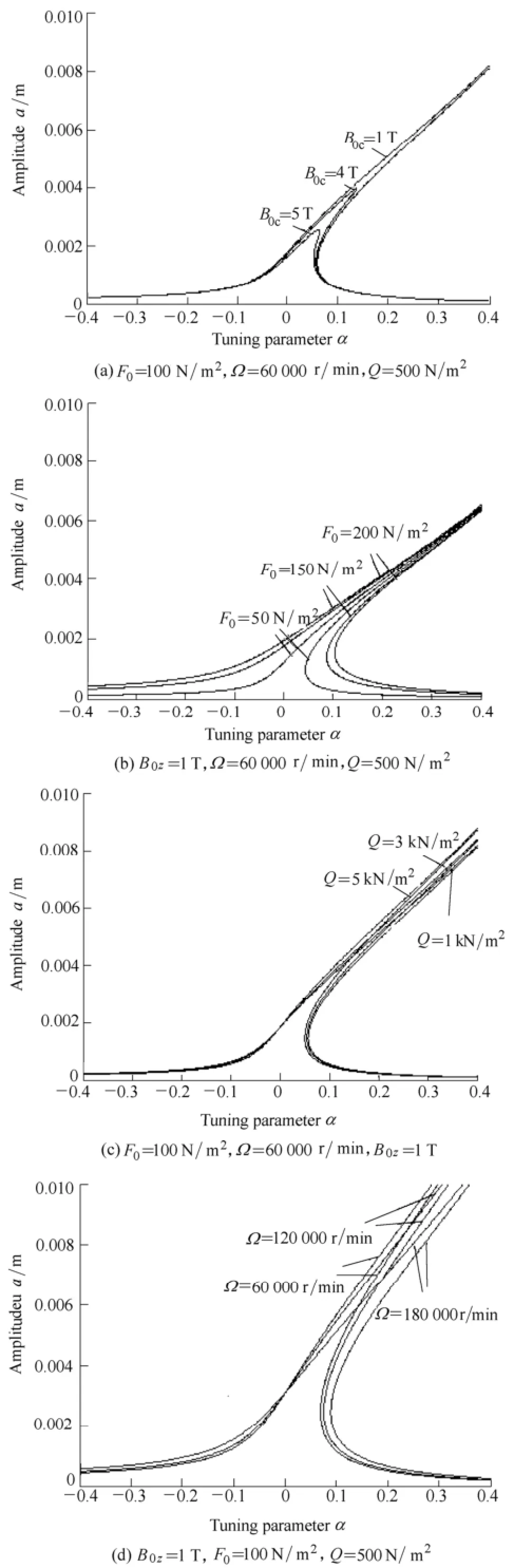
Fig. 2. Amplitude-frequency characteristic curves

Fig. 3 represents the variation of the response amplitude against the excitation force with different tuning parameters. In Fig. 3， R=0.3 m， h=0.004 m， F0=100 N/m2， Ω=60 000 r/min， B0z=1 T. Fig. 3 shows that， when the tuning parameter α is small， the amplitude varies from single solution to three solutions with the static load increasing. As α increasing， the amplitude exists three solutions all the way with the static load increasing. α=0.068 is the critical value. The value of the static load has impact on the multivalued characteristic of the curve.

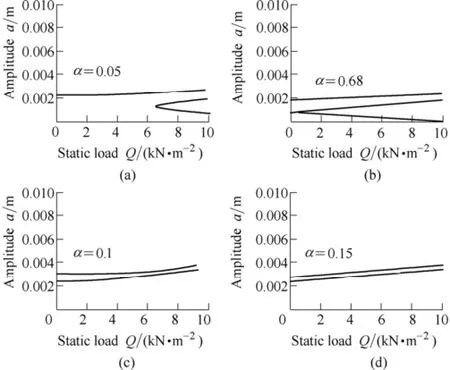
Fig. 3. Amplitude-static load curves for α

Fig. 4 represents the variation of the response amplitude against the excitation force with different static loads. In Fig. 4， R=0.3 m， h=0.004 m， α=0.1， Ω=60 000 r/min，B0z=1 T. From the figure we can see that the curve exists multiple solutions when the value of the excitation force is small. The amplitude increases with the value of the excitation force increasing. When F0=188 N/m2， the curve begin to appear single solution when Q≥0. When F0≥188 N/m2， the amplitude varies from multi-value to singular value as the static load increases.

Fig. 4. Amplitude-static load curves for F0

Fig. 5 represents the curve of the variation of the response amplitude against the value of the excitation force. In Fig. 5， R=0.3 m， h=0.004 m， Q=500 N/m2， Ω=60 000 r/min， B0z=1 T. The figure shows that， the small excitation force can cause the resonance of the system and there exist multiple solutions when the tuning parameter is small. The curve changes to exist a larger single solution with the increasing of the excitation force. Fig. 6 represents the variation of the response amplitude against the value of the excitation force with different values of magnetic induction intensity.

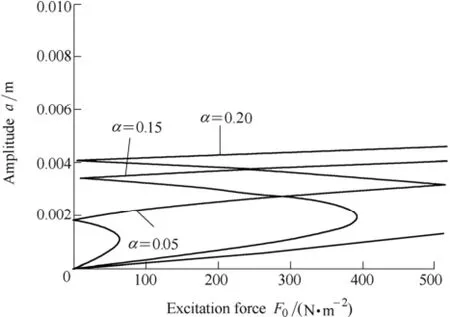
Fig. 5. Amplitude-excitation force curves for α

In Fig. 6， R=0.3 m， h=0.004 m， Q=500 N/m2， α=0.1，Ω=60 000 r/min. The greater the magnetic induction intensity is， the greater the amplitude of the excitation required by multiple solutions is.

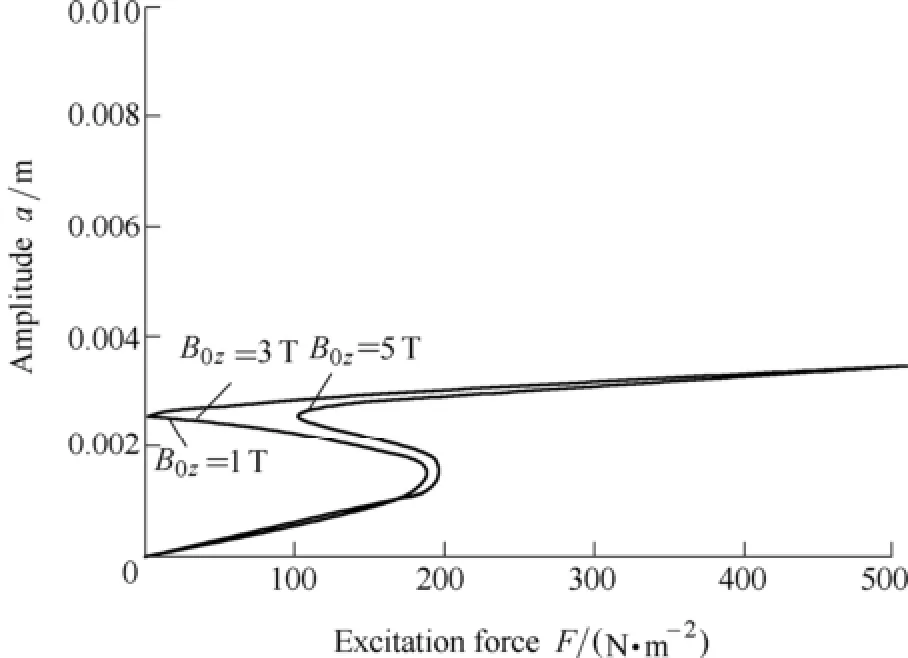
Fig. 6. Amplitude- excitation force curves for B0z

Fig. 7 represents the curves of the variation of the response amplitude against the value of the excitation force with different static loads. In Fig. 7， R=0.3 m， h=0.004 m，B0z=1 T， Ω=60 000 r/min， α=0.1. Fig. 8 represents the curves of the variation of the response amplitude against the value of the excitation force with different spinning velocities. In Fig. 8， R=0.6 m， h=0.008 m， B0z=1 T， α=0.1，Q=500 N/m2. There is not only single solution but also multiple solutions which have relation with the values of the static loads and the spinning velocity.

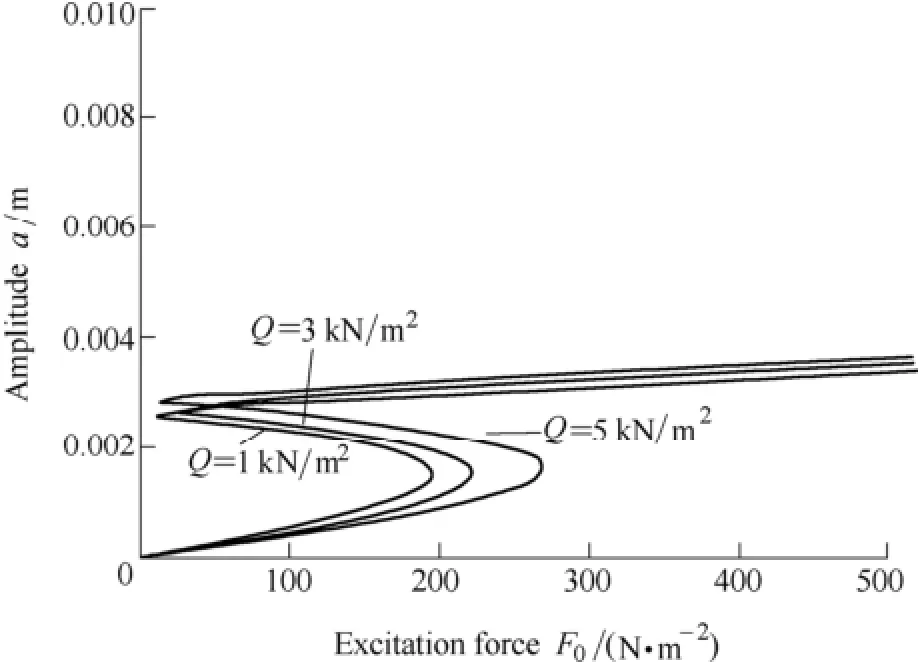
Fig. 7. Amplitude-excitation force curves for Q

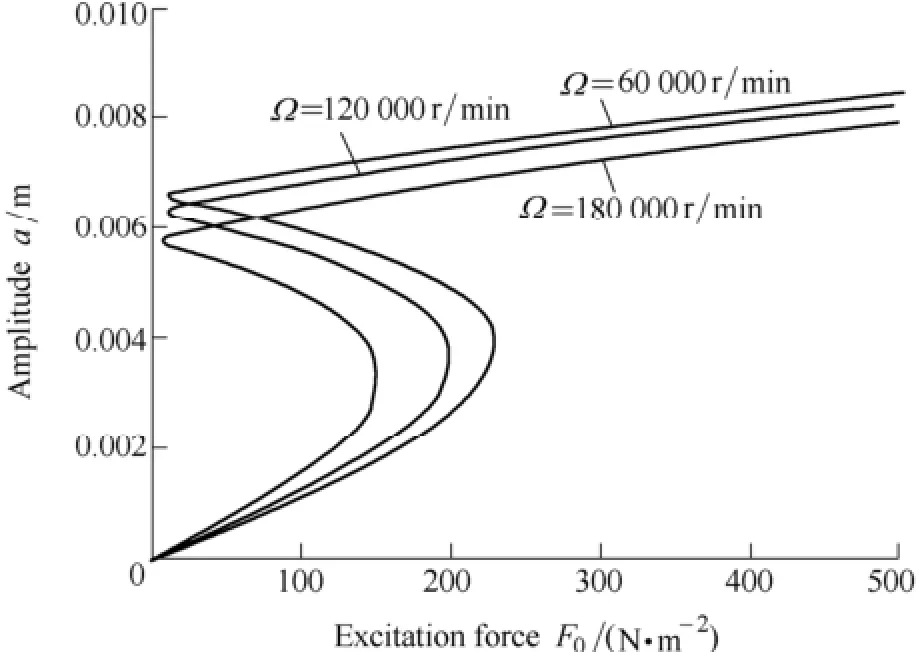
Fig. 8. Amplitude- excitation force curves for Ω

6 Conclusions

（1） The value of the amplitude of the resonance increases as the static load increases. The characteristic of the hard spring is obvious.

（2） The resonance amplitude decreases obviously with the magnetic induction intensity increasing. The vibration of the system can be controlled by choosing the proper value of the magnetic induction intensity.

（3） The amplitude increases obviously in the region of the resonance and has multiple solutions. Some parameters such as the spinning velocity have influence on the resonance of the system.

［1］ MARETIC R， GLAVERDANOV V， MITIC V M. Vibration and stability of rotating annular disks composed of different materials［J］. Archive of Applied Mechanics， 2015， 85（1）: 117-131.

［2］ ALIJANI F， AMABILI M， FERRARI G， et al. Nonlinear vibrations of laminated and sandwich rectangular plates with free edges. Part 2: Experiments & comparisons［J］. Composite Structures， 2013， 105: 437-445.

［3］ JANGHORBAN M， ROSTAMSOWLAT I. Free vibration analysis of functionally graded plates with multiple circular and non-circular cutouts［J］. Chinese Journal of Mechanical Engineering， 2012， 25（2）: 277-284.

［4］ HUANG X L， SHEN H S. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments［J］. International Journal of Solids and Structures， 2004， 41（9-10）: 2403-2427.

［5］ ALLAHVERDIZADEH A， NAEI M H， BAHRAMI M N. Nonlinear free and forced vibration analysis of thin circular functionally graded plates［J］. Journal of Sound and Vibration， 2008，310（4-5）: 966-984.

［6］ WANG Yongang， GAO Dan， WANG Xinzhi. On the nonlinear vibration of heated corrugated circular plates with shallow sinusoidal corrugations［J］. International Journal of Mechanical Sciences， 2008， 50（6）: 1082-1089.

［7］ RANJAN V， GHOSH M K. Transverse vibration of thin solid and annular circular plate with attached discrete masses［J］. Journal of Sound and Vibration， 2006， 292（3-5）: 999-1003.

［8］ GORMAN D G， LEE C K， REESE J. Vibration analysis of a thin circular plate influenced by liquid/gas interaction in a cylindrical cavity［J］. Journal of Sound and Vibration， 2005， 279（3-5）: 601-608.

［9］ JEONG K H. Free vibration of two identical circular plates coupled with bounded fluid［J］. Journal of Sound and Vibration， 2003，260（4）: 653-670.

［10］ HASHEMI S H， FARHAD S， CARRA S. Free vibration analysis of rotating thick plates［J］. Journal of Sound and Vibration， 2009，323（1-2）: 366-384.

［11］ MARETIC R. Transverse vibration and stability of an eccentric rotating circular plate［J］. Journal of Sound and Vibration， 2005，280（3-5）: 467-478.

［12］ NAYFEH A H， JILANII A， MANZIONE P. Transverse vibrations of a centrally clamped rotating circular disk［J］. Nonlinear Dynamics，2001， 26（2）: 163-178.

［13］ BAUER H F， EIDELW. Transverse vibration and stability of spinning circular plates of constant thickness and different boundary conditions［J］. Journal of Sound and Vibration， 2007， 300（3-5）: 877-895.

［14］ DU Guojun， MA Jianqing. Nonlinear vibration and buckling of circular sandwich plate under complex load［J］. Applied Mathematics and Mechanics（English Edition）， 2007， 28（8）: 1081-1091.

［15］ DU Guojun， LI Huijian. Nonlinear vibration of circular sandwich plate under the uniformed load［J］. Applied Mathematics and Mechanics（English Edition）， 2000， 21（2）: 217-226.

［16］ YUAN Hong， LIU Renhuai. Nonlinear vibration of corrugated shallow shells under uniform load［J］. Applied Mathematics and Mechanics（English Edition）， 2007， 28（5）: 514-520.

［17］ GAO Yuanwen， XU Bang， HUH H. Electromagneto-thermomechanical behaviors of conductive circular plate subject to time-dependent magnetic fields［J］. Acta Mechanica， 2010（1-2）， 210: 99-116.

［18］ HU Yuda， ZHANG Zhiqiang. The bifurcation analysis on the circular functionally graded plate with combination resonances［J］. Nonlinear Dynamics， 2012， 67（3）: 1779-1790.

［19］ HU Yuda， LI Jing. Magneto-elastic combination resonances analysis of current-conducting thin plate［J］. Applied Mathematics and Mechanics（English Edition）， 2008， 29（8）: 1053-1066.

［20］ HU Yuda， ZHANG Yiying. Analysis of magneto-elastic principal resonance of axially moving［J］. Journal of Mechanical Engineering，2013， 49（23）: 123-128.

［21］ RECKTENWALD G， RAND R. Stability of strongly nonlinear normal modes［J］. Communications in Nonlinear Science and Numerical Simulation， 2007， 12: 1128-1132.

［22］ HU Yuda， DU Guojun. Free vibration of a thin round plate in magnetic field［J］. Engineering Mechanics， 2007， 24（7）: 184-188.（in Chinese）

［23］ XU Zhilun. Elasticity［M］. Beijing: Higher Education Press， 2006.（in Chinese）

Biographical notes

HU Yuda， born in 1968， is currently a professor at Yanshan University， China. He received his PhD degree from Tianjin University， China. His research interests include magneto elastic dynamics.

Tel: +86-335-8074576； Email: huyuda03@163.com

WANG Tong， born in 1990， is currently a master candidate at Yanshan University， China. She received her bachelor degree from Yanshan University， China， in 2012. Her research interests include magneto elastic nonlinear vibration.

E-mail: 792729663@qq.com

10.3901/CJME.2015.0720.097， available online at www.springerlink.com； www.cjmenet.com； www.cjme.com.cn

* Corresponding author E-mail: huyuda03@163.com

Supported by National Natural Science Foundation of China（Grant No. 11472239）， Hebei Provincial Natural Science Foundation of China（Grant No. A2015203023）， and Key Project of Science and Technology Research of Higher Education of Hebei Province of China（Grant No. ZD20131055）

© Chinese Mechanical Engineering Society and Springer-Verlag Berlin Heidelberg 2015

April 7， 2015； revised July 16， 2015； accepted July 20， 2015