Singularity Analysis of a 3-RPS Parallel Manipulator Using Geometric Algebra

LI Qinchuan*， XIANG Ji'nan， CHAI Xinxue， and WU Chuanyu

Mechatronic Institute， Zhejiang Sci-Tech University， Hangzhou 310018， China



Singularity Analysis of a 3-RPS Parallel Manipulator Using Geometric Algebra

LI Qinchuan*， XIANG Ji'nan， CHAI Xinxue， and WU Chuanyu

Mechatronic Institute， Zhejiang Sci-Tech University， Hangzhou 310018， China

Singular configurations must be avoided in path planning and control of a parallel manipulator. However， most studies rarely focus on an overall singularity loci distribution of lower-mobility parallel mechanisms. Geometric algebra is employed in analysis of singularity of a 3-RPS parallel manipulator. Twist and wrench in screw theory are represented in geometric algebra. Linear dependency of twists and wrenches are described by outer product in geometric algebra. Reciprocity between twists and constraint wrenches are reflected by duality. To compute the positions of the three spherical joints of the 3-RPS parallel manipulator， Tilt-and-Torsion angles are used to describe the orientation of the moving platform. The outer product of twists and constraint wrenches is used as an index for closeness to singularity（ICS） of the 3-RPS parallel manipulator. An overall and thorough perspective of the singularity loci distribution of the 3-RPS parallel manipulator is disclosed， which is helpful to design， trajectory planning and control of this kind of parallel manipulator.

singularity， parallel manipulator， geometric algebra

1 Introduction*

A parallel mechanism is defined as a closed-loop system that consists of an end-effector and a fixed base， linked by several independent kinematic chains［1］. When the number of the degrees of freedom（DOF） of a parallel mechanism is less than six， it is called a lower-mobility parallel mechanism. Lower-mobility parallel manipulator gains growing concerns in recent years［2］because it has advantages of simple structure， low cost in manufacturing，and easier control over its counterparts with six DOFs.

Singularity is an inherent characteristic of parallel manipulators. In its singular configuration， a parallel manipulator loses its rigidity， and the end-effector becomes uncontrollable. Much progress has been obtained in terms of singularity analysis. GOSSELIN， et al［3］， investigated the singularity based on the deficiency of Jacobian matrices. ZLATANOV， et al［4］， expanded the approach proposed by GOSSELIN， et al［3］， divided singularity into six types. TSAI［5］made similar classification based on Jacobian matrix， and he named three different kinds of singularities，that is， inverse kinematic singularity， direct kinematic singularity， and combined singularity. CHOI， et al［6］，studied the singularity of a four-DOF H4 parallel manipulator using an expanded Jacobian matrix instead of a conventional one to achieve a better result. HUNT［7］laid the foundation for the methodology for analyzing parallel singularity via screw theory. MERLET［8］identified all singular configuration of a triangular simplified symmetric manipulator using Grassmann line geometry. Although this method obtains an exhaustive list of singular configurations，it is tough to express the geometric condition analytically. JOSHI， et al［9］， studied the Jacobian matrix derived by using screw theory and determined the singular configurations of the 3-RPS manipulator. PARK and KIM［10］， investigated singularities of closed kinematic chains by differential geometry using their geometric framework mainly for the manipulability of closed chains proposed in Refs. ［11-12］. HUANG， et al［13］， and LI， et al［14］， investigated the kinematic principle and geometric condition for general-linear-complex special configuration. Some researchers［15-17］studied singularity analysis of lower-mobility parallel mechanism using Grassmann-Cayley algebra.

In 1840s， Hermann Grassmann proposed geometric algebra［18］. In 1870s， William Clifford， standing on the shoulders of Hamilton and Grassmann， furthered their work. In Clifford's manuscript， it is found that the geometrical features of vector， plane， and high-dimensional objects are described by his algebra. However， after nearly a hundred years of silence， HESTENES［19］proposed it again in 1960s. And then， researchers， including D'ORANGEVILLE and LASENBY［20］， DORST， et al［21］，PERWASS， et al［22］， made valuable contributions to the development of geometric algebra.

Geometric algebra combines geometric conditions with algebraic equations， which is a distinct advantage of expressing the geometric relationship of the joints of a mechanism. One main property of geometric algebra is that subspaces can be added， subtracted and intersected in its framework. Geometric algebra has obvious interpretative advantages over other methods when dealing with geometric applications.

Application of geometric algebra covers physics， neural computing， robotics， signal and image processing，computer and robot vision. SELIG［23］lectured on the applications of Clifford algebra in engineering， especially in computer vision and robot kinematics. HIDENBRAND，et al［24］， computed 3-dimensional inverse kinematics in the 5-dimensional conformal algebra， which made use of the straightforward characteristic of geometric algebra. WANG，et al［25］， and FU， et al［26］， investigated the inverse kinematics of serial manipulators.

However， geometric algebra is seldom applied to singularity analysis of lower-mobility parallel manipulators. To the best of our knowledge， in 2006 and 2008，TANEV［27-28］proposed a methodology for deriving the singularity condition for lower-mobility parallel mechanism using geometric algebra， and then he analyzed the linear dependency of the blades of a mechanism qualitatively and identified the singularity. ZHANG［29］discussed the singularity of a 3-RPS parallel mechanism by analyzing its blades from a qualitative perspective based on TANEV's pioneering work［27］.

Employing TANEV's method［27-28］， this paper obtains the general singularity locus and the constraint singularity locus of the 3-RPS parallel manipulator from a quantitative perspective. The paper is structured as follows. Section 2 introduces the basics of geometric algebra. Section 3 introduces the singularity analysis based on geometric algebra in the lower-mobility parallel mechanism. Section 4 illustrates an example to adopt the methodology for analyzing singularity of lower-mobility parallel mechanism numerically. The inverse kinematics of HUNT's 3-RPS parallel manipulator is solved via Tilt-and-Torsion angles instead of traditional Euler or Tait-Bryan angles. Based on the coordinates of the three S joints， the screws are obtained and they are expressed in G6. Singular configurations of the 3-RPS manipulator are drawn in distribution loci generated in Maple. Finally， constraint singularity of the 3-RPS manipulator is analyzed by similar approach.

2 Basics of Geometric Algebra

Geometric algebra is the fusion of geometry and algebra. It can be more direct and efficient to solve mathematical problem than any other mathematical system， like tensor，vector algebra， complex algebra. Moreover， it integrates different kinds of algebraic systems to obtain a unified mathematical language， which not only preserves different special feature， but also has new features that other algebra does not have.

2.1 Geometric operators

The element of a geometric algebra G is called a multi-vector. It is assumed that G is closed under addition and multiplication between multi-vectors. A blade A for a k-dimensional subspace of Rnis a product of members of an orthogonal basis for the subspace， namely，A=a1a2⋅⋅⋅ak. We call A a blade of grade k. Every multi-vector A in G can be expressed as

The three fundamental operators are geometric product，inner product， and outer product. They are shown as follows， respectively:

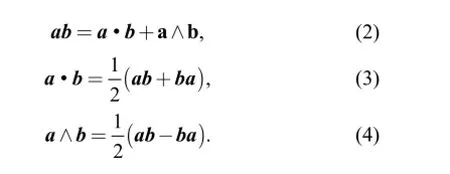
2.2 Properties of three products

The outer product is the anti-commutative， namely，

a∧b=-b∧a. It also satisfies the associative law and the distributive law， namely， a∧（b+c）=a∧b+a∧c， a∧（b∧c）=（a∧b）∧c.

Three vectors are linearly dependent if and only if their outer product is zero，

Thus， outer product makes linear dependency a computational property.

2.3 Duality

If Aris a blade， the dual of Aris the orthogonal complement of Ar. The dual of Aris spanned by the bases not contained in Ar［22］. Duality can be used to express the constraint space of a mechanism from its motion space. The dual of a multi-vector A is obtained by geometrically multiplying A with the inverse of a unit pseudoscalar. Here，in G3， the unit pseudoscalar is I3=e1e2e3； in G6， I6=e1e2e3e4e5e6is the unit pseudoscalar.is theinverse of I6. Let Ak=S1∧S2∧⋅⋅∧Sk， then in G6，denotes the dual of A.k

A directional line in space can be decided by its direction u and moment m:

where r is the position vector of any point on the line l.

A screw S can be expressed as a vector in G6with the basis ｛e1，e2，e3，e4，e5，e6｝ and

where k1， k2， and k3denote the three direction cosines of the vector and k4， k5， and k6denote the three components of the moment of the vector.

3 Method for Singularity Analysis of Lower-mobility Parallel Mechanisms

3.1 Blades of limb motion Sijis defined as the jth joint twist of the ith limb of a lower-mobility parallel mechanism. Let Aidenote the blade of the end motion of the ith limb. It can be defined as the outer product of all mitwists of the ith limb:

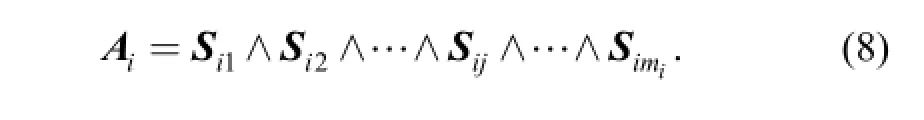
The blade of a limb motion Aican be interpreted as a subspace which is spanned by all the mitwists of the ith limb.

3.2 Blades of limb constraint

In G6， the dual of Aiis as

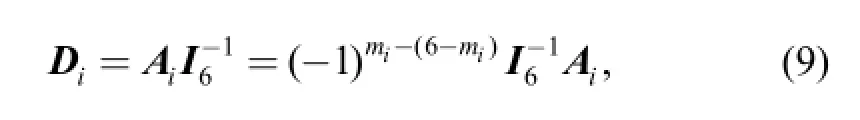
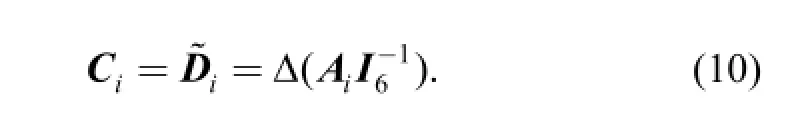
The blade of the constraint of the ith limb is defined asis obtained through a reciprocal transformation in G6that interchanges the order of the primary part and the secondary part of Di. According to Eq. （8） and the definition of duality， Ciis a blade of grade （6-mi） which denotes a subspace spanned by all the constraint wrenches of the ith limb. Obviously， it represents the constraint space of the ith limb.

3.3 Blades of platform constraint

Based on the blade of limb constraint， the blade of platform constraint is

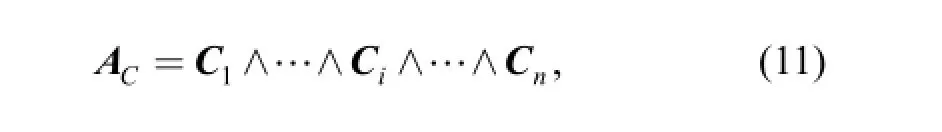
where ACis a p-blade representing the constraint subspace spanned by all the constraint wrenches of n limbs.

3.4 Dummy joint

Some legs of a lower mobility parallel mechanism may not have full mobility. In that case， it is supposed that the remaining DOFs are represented by dummy joints （or driven but locked joints） and associated with them dummy screws［27］.

3.5 Singular condition

The singular condition developed from the linear dependency of the blades representing active and dummy joints is proposed by TANEV［28］:

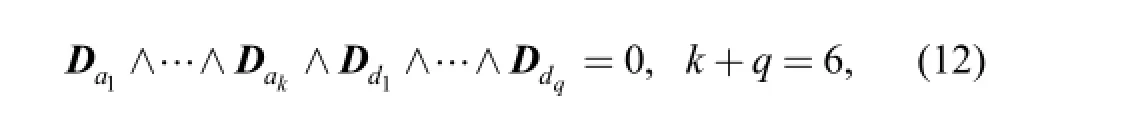
whereiaD is the dual vector associated with the ith actuated joint，idD is the dual vector associated with the ith dummy joint.

The result obtained from Eq. （12） contains kinematic singularities and constraint singularities. However， one cannot identify constraint singularities from the mixed results. In order to obtain the constraint singularity， Eq. （13）was used to achieve this goal. When constraint singularity occurs， we have

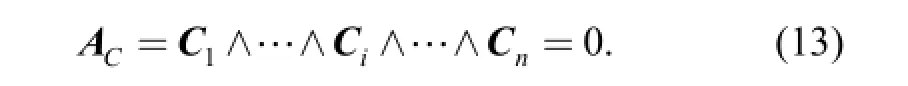
In fact，iC isidD defined by TANEV in Ref. ［27］.

4 Singularity of 3-RPS Parallel Manipulator

Fig. 1 shows the schematics of the 3-RPS parallel manipulator proposed by HUNT［30］in 1983. The three P joints are actuated. This manipulator has one translational and two rotational DOFs［31］.

4.1 Positions of three S joints

Tilt-and-Torsion angles［32-33］are adopted in the process of analyzing singularity. Tilt-and-Torsion angles are modified Euler angles. Because HUNT's 3-RPS parallel manipulator is without torsion angle， the number of rotation angles is reduced to two. The reduction of rotation angles simplifies the following expressions.

Coordinate frames are established as shown in Fig. 1. The origin of frame -o xyz′ is located at the center of the moving platform， and the origin of frame oXYZ- is located at the center of the base. The radius of the circumscribed circle of the moving platform and the baseare r=400 mm and r2=500 mm， respectively. The height of the moving platform is kept as constant at h=1300 mm. Note that the height can be any value. Here h=1300 mm is chosen as an example to illustrate the method.

Fig. 1. Schematics of a 3-RPS parallel manipulator

Let the rotation matrix of frame -o xyz′ with respect to frame oXYZ- be R:

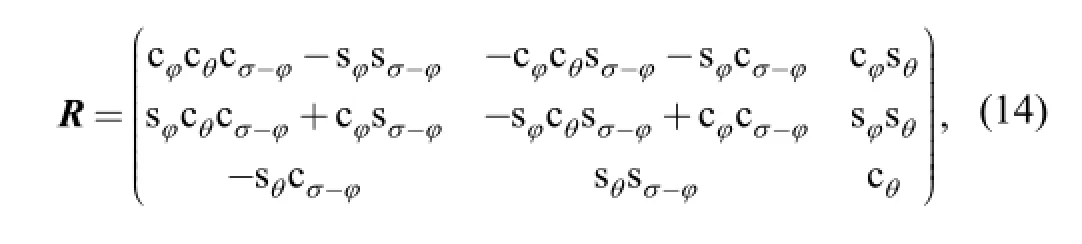
where c is shorthand for cosine， s for sine， and φ， θ， and σ are angles representing azimuth， tilt and torsion，respectively. Since the 3-RPS parallel manipulator has no torsion angle， σ equals zero.

The position vectors of S joints，1B，2B， and3B， with respect to the base frame oXYZ- are1R，2R， and3R，respectively:

4.2 Singularity analysis

From Eqs. （15）-（17）， the twist system of the 3-RPS parallel manipulator can be obtained in Plücker coordinates，and it is written in the form of a vector in G6with the basis｛e1，e2，e3，e4，e5，e6｝.

Each twist of limb i can be written as

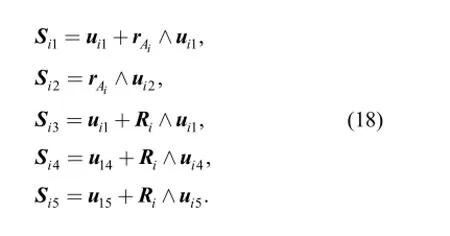
In Eq. （18）， uijdenotes the direction component of the jth twist of the ith limb， rA1， rA2， rA3are the position vectors of points A1， A2， A3， respectively.

It is self-evident that the expressions depend only on two rotation angles. Because of its symmetrical layout， we analyzed limb 1 first as shown in Fig. 2.

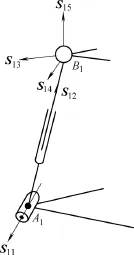
Fig. 2. First limb of the 3-RPS parallel manipulator

4.2.1 General singularity

The dual vector，2iD， associated to the actuated P joint and the dual vector，idD， associated to the dummy joint are as follows:

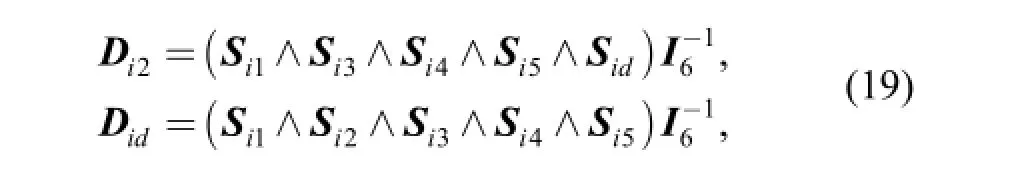
where subscript d represents dummy joint. The RPS leg has five DOFs and one extra dummy joint（denoted by a subscript d） is added to make it full mobility. The extra dummy joint can be considered as active but locked［30］.

For limb 1， the outer product of2iD andidD is

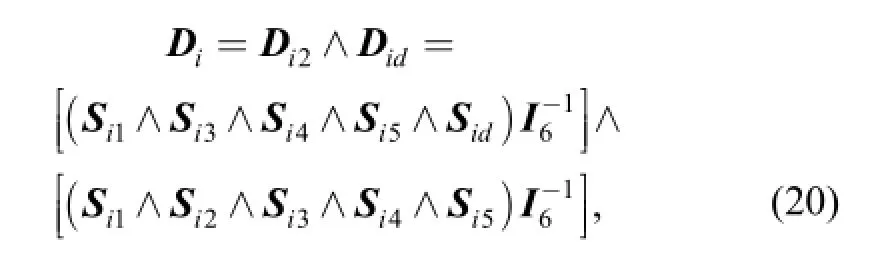
where 1i=.

Simplifying Eq. （20） gives

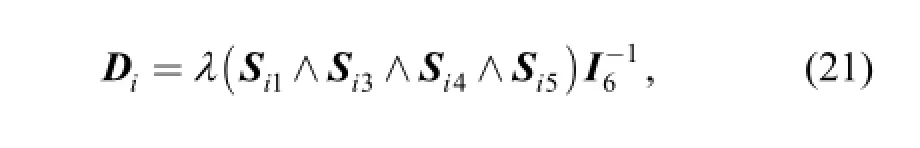
where i=1，and λ=（Si1∧Si3∧Si4∧Si5∧Sid∧Si2is a constant.

Based on the singular condition proposed in Eq. （12） by TANEV［28］，

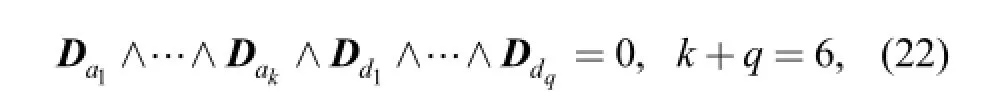
whereiaD is the dual vector associated to the ith actuated joint，idD is the dual vector associated to the ith dummy joint. The singular condition of the 3-RPS parallel manipulator is given as

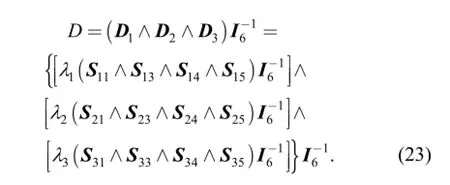
Then， programming and calculating is conducted instead of resorting to discussing the geometry of the twist system. When the height of the moving platform is at h=1300 mm ， the distribution of value D of every configuration is shown in Fig. 3. The manipulator is in its singular configuration if D=0 as shown in Fig. 3. Note that D actually describes the closeness of the 3-RPS parallel mechanism to the singularity. It is thus called index for closeness to singularity（ICS）.

Fig. 3. Distribution of value D of every configuration when h=1300 mm

Several points in Fig. 4（a） are taken as examples to illustrate the singular configurations. The coordinates are rounded to three decimal places. Constraint singularity in Fig. 4（a） is drawn red in Fig. 4（b）. This means that general singularity contains constraint singularity， which will be detailed in the next section.

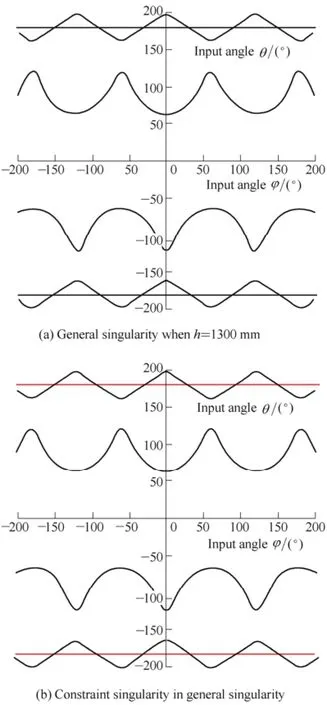
Fig. 4. Singularity distribution when h=1300 mm

Fig. 5 is the loci of singularity distribution for every height h of the moving platform， which ranges from 0 to 1300 mm. Moreover， Fig. 6 shows the singularity distribution for several heights of the moving platform，namely h=0.2 m ， h=0.4 m ， h=0.6 m， h=0.8 m ，h=1.0m， and h=1.2 m.

When φ=0.000，θ=180.023°， the position vectors of three S joints， R1， R2， and R3， are （-800.000 0.000 13）T，（-200.000 346.410 1300.000）T， （-200.000 -346.410 1300.000）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（a）. This is a constraint singularity， which will be further explained in the following.

When φ=0.000，θ=64.687°， the position vectors of three S joints， R1， R2， and R3， are （56.421 0.000 938.369）T，（-200.000 346.410 1480.815）T， （-200.000 -346.410 1480.815）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（b）. This is a 5b singular configuration in the classification of MERLET［8］and an RO-type singularity［34］.

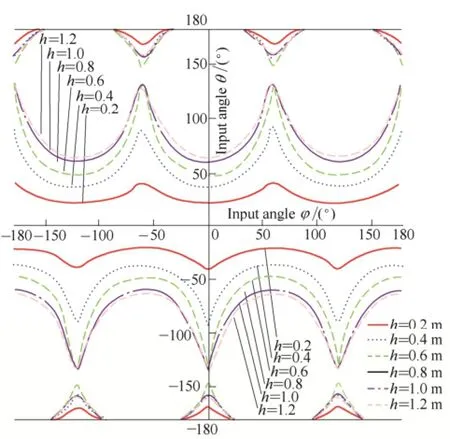
Fig. 6. Singularity distribution for several heights of the moving platform

When φ=0.000，θ=-121.754°， the position vectors of three S joints， R1， R2， and R3， are （-515.972 0.000 1640.040）T， （-200.000 346.410 1129.980）T， （-200.000 -346.410 1129.980）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（c）. This is similar to Fig. 7（b）. It is also a 5b singular configuration in the classification of MERLET［8］and an RO-type singularity［34］.

When φ=0.000，θ=-161.631°， the position vectors of three S joints， R1， R2， and R3， are （-769.429 0.000 1426.053）T， （-200.000 346.410 1236.974）T， （-200.000 -346.410 1236.974）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（d）. This is a 5b singular configuration in the classification of MERLET［8］and the sixth kind of singularity［35］.

When φ=28.648°，θ=-179.221°， the position vectors of three S joints， R1， R2， and R3， are （-432.205 0.000 1340.669）T， （-399.546 692.034 1299.874）T， （183.417 317.687 1295.456）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（e）. This is a 5b singular configuration in the classification of MERLET［8］.

When φ=40.107°，θ=90.069°， the position vectors of three S joints， R1， R2， and R3， are （131.764 0.000 994.063）T， （-287.763 498.420 1229.805）T， （53.924 97.398 1676.132）T， respectively. The schematic representation of the manipulator at this point is presented in Fig. 7（f）. In this configuration， the moving platform is perpendicular to the base. This is a 5a singular configuration in the classification of MERLET［8］.

Fig. 7. Part of the singular configurations when h=1300 mm

4.2.2 Constraint singularity

The definition of constraint singularity by ZLATANOV［34］is adopted to analyze the constraint singularity of the 3-RPS parallel manipulator. The procedure for constraint singularity analysis is explained as follows. The program flowchart is shown in Fig. 8.

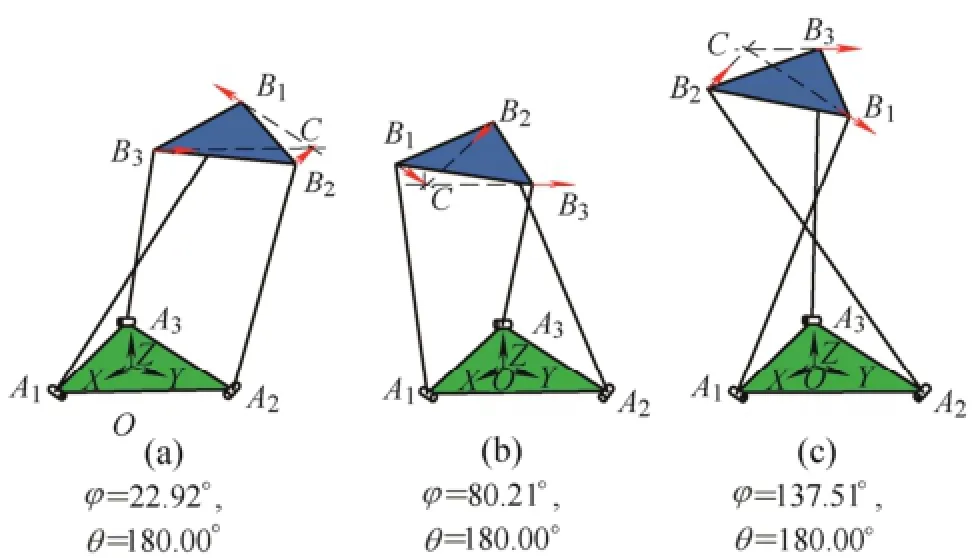
Fig. 8. Several constraint singularities when h=1300 mm

（1） Express all the twist of the ith limb and calculate the blade of limb motionof ith limb

Given the expressions of all the twists， we calculate the blade of limb motion of each limb by outer product

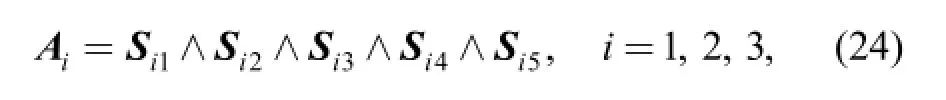
（2） Calculate the blade of the limb constraintof the ith limb

The dual of the blade of the ith limb motion is

Interchanging the order of the primary part and the secondary part ofyields

（3） Calculate the blade of platform constraint Ac

The outer product of the all the constraint wrenches of three limbs， namely， gives the blade of platform constraint Ac:

（4） Find the φ and θ of constraint singularity

If constraint singularity occurs， Acwill equal zero. Here，numerical search is used to obtain the result of singularity. From （3）， the coefficients of Acare obtained. If the absolute values of these coefficients are all smaller than a certain threshold and all near zero， then the corresponding configuration is in constraint singularity.

Two rotation angles， θ and φ， range from 0° to 360°. Several constraint singularities of the manipulator are shown in Fig. 9 where the big and green triangle denotes the base， and the small and blue triangle the moving platform. The red arrow represents a constraint force， and point C is the intersection of three constraint forces. The coordinates of three R joints in constraint singular configurations are shown in Table 1. Note that the height of the moving platform is h=1300 mm .

From Fig. 8 and Table 1， the result of constraint singularity analysis is consistent with Ref. ［34］， which turns out that if θ=180°， that is， the moving platform and the base are parallel and the moving platform is upside down，the manipulator is in its constraint singularity.

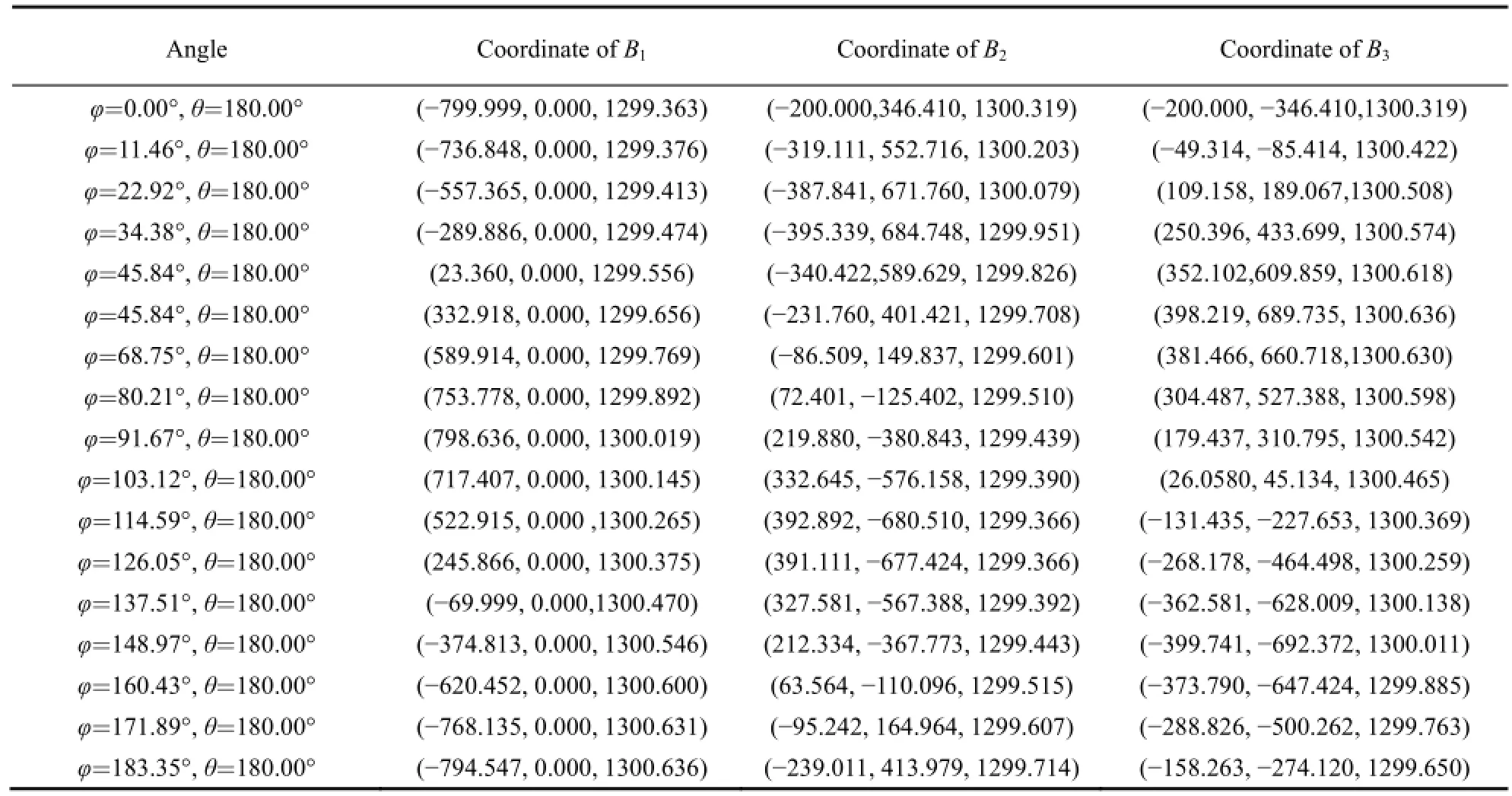
Table 1. Coordinates of three S joints in constraint singularity when h=1300 mm

5 Conclusions

（1） Overall kinematic and constraint singularity loci distributions of the 3-RPS parallel manipulator are obtained in the framework of geometric algebra. The results of singularity distribution provides a powerful tool in the context of design and application of such manipulators.

（2） Geometric algebra provides a complete representation of twist and wrench. The reciprocity between twist and wrench is reflected by their duality in geometric algebra. This method is computationally advantageous and can be applied to singularity analysis of other classes of parallel manipulators.

［1］ MERLET J P. Parallel robots［M］. Dordrecht: Springer， 2001.

［2］ LIU Xinjun， WANG Jinsong. Parallel kinematics: Type， kinematics，and optimal design［M］. Berlin: Springer Science & Business Media，2013.

［3］ GOSSELIN C， ANGELES J. Singularity analysis of closed-loop kinematic chains［J］. IEEE Transactions on Robotics and Automation， 1990， 6（3）: 281-290.

［4］ ZLATANOV D， FENTON R G， BENHABIB B.Singularity analysis of mechanisms and robots via velocity-equation model of the instantaneous kinematics［C］//Proceedings of the 1994 IEEE International Conference on Robotics and Automation， San Diego，California， USA， May 8-13， 1994: 980-985.

［5］ TSAI Lungwen. Robot analysis: the mechanics of serial and parallel manipulators［M］. New York: John Wiley & Sons， 1999.

［6 ］ CHOI H， RYU J. Singularity analysis of a four degree-of-freedom parallel manipulator based on an expanded 6 × 6 Jacobian matrix［J］. Mechanism and Machine Theory， 2012， 57（0）: 51-61.

［7］ HUNT K H. Kinematic geometry of mechanisms［M］. Oxford: Clarendon Press， 1990.

［8］ MERLET J P. Singular configurations of parallel manipulators and Grassmann geometry［J］. The International Journal of Robotics Research， 1989， 8（5）: 45-56.

［9］ JOSHI S A， TSAI L W. Jacobian analysis of limited-DOF parallel manipulators［J］. Journal of Mechanical Design， 2002: 341-348.

［10］ PARK F C， KIM J W. Singularity analysis of closed kinematic chains［J］. Journal of Mechanical Design， 1999， 121（1）: 32-38.

［11］ PARK F C， KIM J W. Manipulability of closed kinematic chains［J］. Journal of Mechanical Design， 1998， 120（4）: 542-548.

［12］ PARK F C， KIM J W. Kinematic manipulability of closed chains［M］//Recent Advances in Robot Kinematics. Netherlands: Springer， 1996: 99-108.

［13］ HUANG Z， ZHAO Y， WANG J， et al. Kinematic principle and geometrical condition of general-linear-complex special configuration of parallel manipulators［J］. Mechanism and Machine Theory，1999， 34（8）: 1171-1186.

［14］ LI Y， HUANG Z， WANG L. The singularity analysis of 3-RPS parallel manipulator［C］//Proceedings of the 2006 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference，Philadelphia， Pennsylvania， USA ， September 10-13， 2006: 949-955.

［15］ BEN-HORIN P， SHOHAM M. Singularity condition of six-degree-of-freedom three-legged parallel robots based on Grassmann-Cayley algebra［J］. IEEE Transactions on Robotics，2006， 22（4）: 577-590.

［16］ CARO S， MOROZ G， GAYRAL T， et al. Singularity analysis of a six-dof parallel manipulator using Grassmann-Cayley algebra and groebner bases［M］//Brain， Body and Machine. Berlin Heidelberg: Springer， 2010: 341-352.

［17］ KANAAN D， WENGER P， CHABLAT D. Singularity analysis of limited-DOF parallel manipulators using Grassmann-Cayley algebra［M］//Advances in robot kinematics: Analysis and design. Netherlands: Springer， 2008: 59-68.

［18］ CLIFFORD P. Applications of Grassmann's extensive algebra［J］. American Journal of Mathematics， 1878， 1（4）: 350-358.

［19］ HESTENES D. Space-time algebra［M］. New York: Gordon and Breach， 1966.

［20］ D'ORANGEVILLE C， LASENBY A N. Geometric algebra for physicists［M］. Cambridge : Cambridge University Press， 2003.

［21］ DORST L， FONTIJNE D， MANN S. Geometric algebra for computer science（revised edition）: An object-oriented approach to geometry［M］. Burlington: Morgan Kaufmann， 2009.

［22］ PERWASS C， EDELSBRUNNER H， KOBBELT L， et al. Geometric algebra with applications in engineering［M］. Berlin: Springer， 2009.

［23］ SELIG J M. Clifford Algebras in Engineering［M］//ABŁAMOWICZ R， SOBCZYK G. Lectures on Clifford（Geometric） Algebras and Applications. Boston: Birkhäuser， 2004: 135-156.

［24］ HILDENBRAND D， ZAMORA J， BAYRO-CORROCHANO E. Inverse kinematics computation in computer graphics and robotics using conformal geometric algebra［J］. Advances in Applied Clifford Algebras， 2008， 18（3-4）: 699-713.

［25］ WANG C， WU H， MIAO Q. Inverse kinematics computation in robotics using conformal geometric algebra［C］//Proceedings of the 2009 International Technology and Innovation Conference， Xi'an，China， October 12-14， 2009: 149.

［26］ FU Z， YANG W， YANG Z. Solution of inverse kinematics for 6R robot manipulators with offset wrist based on geometric algebra［J］. Journal of Mechanisms and Robotics， 2013， 5（3）: 031010.

［27］ TANEV T K， TANEV T K. Singularity analysis of a 4-DOF parallel manipulator using geometric algebra［M］//Advances in Robot Kinematics. Netherlands: Springer， 2006: 275-284.

［28］ TANEV T K. Geometric algebra approach to singularity of parallel manipulators with limited mobility［M］//Advances in Robot Kinematics: Analysis and Design. Netherlands: Springer， 2008: 39-48.

［29］ ZHANG L. Kinematics and character of mechanisms based on geometric algebra［D］. Qinhuangdao: Yanshan University， 2008. （in Chinese）

［30］ HUNT K H. Structural kinematics of in-parallel-actuated robotarms［J］. Journal of Mechanical Design， 1983， 105（4）: 705-712.

［31］ HUANG Z， LI Q， DING H. Theory of parallel mechanisms［M］. Dordrecht: Springer， 2012.

［32］ BONEV I A， ZLATANOV D， GOSSELIN C M. Advantages of the modified Euler angles in the design and control of PKMs［C］// Proceedings of the 2002 Parallel Kinematic Machines International Conference， Chemnitz， Germany， April 23-25， 2002: 171-188.

［33］ BONEV I A. Geometric analysis of parallel mechanisms［D］. Quebec: Laval University， 2002.

［34］ ZLATANOV D， BONEV I A， GOSSELIN C M. Constraint singularities of parallel mechanisms［C］//Proceedings of the 2002 IEEE International Conference on Robotics and Automation，Washington， D.C.， USA， May 11-15， 2002: 496-502.

［35］ LI Yanwen. On singularity of several kinds of spacial parallel manipulator［D］. Qinhuangdao: Yanshan University， 2005. （in Chinese）.

Biographical notes

LI Qinchuan， born in 1975， is currently a professor at Zhejiang Sci-Tech University， China. He received his PhD degree on mechanism design and theory from Yanshan University， China， in 2003. His research interests include mechanism theory of parallel manipulators and application.

Tel: +86-571-86843686； E-mail: lqchuan@zstu.edu.cn

XIANG Ji'nan， born in 1990， is currently a master candidate at Mechatronic Institute， Zhejiang Sci-Tech University， China.

E-mail: xjinan@163.com

CHAI Xinxue， born in 1988， is currently a PhD candidate at Mechatronic Institute， Zhejiang Sci-Tech University， China.

E-mail: jxcxx88@163.com

WU Chuanyu， born in 1976， is currently a professor at Zhejiang Sci-Tech University， China. He received his PhD degree on mechanism design and theory at Zhejiang University， China， in 2002. His research interests include intelligentized agricultural machinery and robotics.

Tel: +86-571-86843352； E-mail: cywu@zstu.edu.cn

10.3901/CJME.2015.0728.103， available online at www.springerlink.com； www.cjmenet.com； www.cjme.com.cn

* Corresponding author. E-mail: lqchuan@zstu.edu.cn

Supported by National Natural Science Foundation of China（Grant No. 51135008）， and Zhejiang Provincial Natural Science Foundation of China（Grant No. LZ14E050005）

© Chinese Mechanical Engineering Society and Springer-Verlag Berlin Heidelberg 2015

January 9， 2015； revised July 21， 2015； accepted July 28， 2015