Statistical Modification Analysis of Helical Planetary Gears based on Response Surface Method and Monte Carlo Simulation

ZHANG Jun* and GUO Fan

School of Mechanical Engineering， Anhui University of Technology， Ma'anshan 243032， China



Statistical Modification Analysis of Helical Planetary Gears based on Response Surface Method and Monte Carlo Simulation

ZHANG Jun* and GUO Fan

School of Mechanical Engineering， Anhui University of Technology， Ma'anshan 243032， China

Tooth modification technique is widely used in gear industry to improve the meshing performance of gearings. However， few of the present studies on tooth modification considers the influence of inevitable random errors on gear modification effects. In order to investigate the uncertainties of tooth modification amount variations on system's dynamic behaviors of a helical planetary gears， an analytical dynamic model including tooth modification parameters is proposed to carry out a deterministic analysis on the dynamics of a helical planetary gear. The dynamic meshing forces as well as the dynamic transmission errors of the sun-planet 1 gear pair with and without tooth modifications are computed and compared to show the effectiveness of tooth modifications on gear dynamics enhancement. By using response surface method， a fitted regression model for the dynamic transmission error（DTE） fluctuations is established to quantify the relationship between modification amounts and DTE fluctuations. By shifting the inevitable random errors arousing from manufacturing and installing process to tooth modification amount variations， a statistical tooth modification model is developed and a methodology combining Monte Carlo simulation and response surface method is presented for uncertainty analysis of tooth modifications. The uncertainly analysis reveals that the system's dynamic behaviors do not obey the normal distribution rule even though the design variables are normally distributed. In addition， a deterministic modification amount will not definitely achieve an optimal result for both static and dynamic transmission error fluctuation reduction simultaneously.

tooth modification， helical planetary gears， response surface method， Monte Carlo simulation

1 Introduction*

Tooth modification has been recognized as one of the most important and effective approaches to increase gear durability and reduce gear dynamic response and noise. Numerous studies have been conducted with concentration on the specific issue of determining tooth modification amounts and their effects on mesh performances such as bending and contact stresses， load distributions and static transmission error（STE） in different types of gear transmissions［1-5］. Compared with abundant investigations of modification effects on gear statics， the researches about influences of modification parameters on gear dynamics are quite scare， not mentioning that the studies focused on the relationship between modification amounts and dynamic responses in planetary gear trains are even fewer. BAHK and PARKER［6-7］revealed that tooth micro-geometry modifications were very influential on the dynamic performances of spur planetary gears. From the mechanics point of view， the dynamic response of a gear system can be regarded as the results of transmission error excitations. Therefore， the essence of tooth modification is to reduce the dynamic transmission error（DTE）， and to be more specific， the fluctuation of dynamic transmission error（ΔDTE） of a gear system. With this thought， some studies on gear dynamics including KAHRAMAN［8］，TAMMINANA［9］and HOTAIT［10］， et al， used DTE as a metric to quantify the gear dynamic behaviors. However，the determination of modification amounts is not an easy task in that the relationship between modification amounts and DTE is implicit due to the complex nonlinearity of a gear system. For such kind of dilema， the response surface method provides an effective way to estimate a complex unknown function or the actual but implicit limit state function with a first-order model or a second-order model. The response surface method has become a standard approach for most of the experimentations carried out in a variety of research fields［11-15］. For example， PARK［16］used this method to built a fitted regression model to predict the STE of a gear pair with modifications， based on which a robust tooth surface analysis was conducted. As to the author's best knowledge， quantitative relationship between modification amounts and STE or DTE in planetary gear trains has not yet been proposed or publically exposed.

Another point worthy to mention is that almost all of the above researches were based on deterministic methods and did not account for the inevitable randomness of process parameter variations of tooth modification amounts and shapes. As far as a real gear structures is concerned， tooth modification amounts and shapes are random variations due to manufacturing and installing errors as well as component deformations， which makes gear deterministic modification simplification generally impractical and thus may probably limit the effectiveness of tooth modifications on gear performances. Therefore， from a practical point of view a statistical modification model involving uncertainty analysis is of great necessary when evaluating the modification effects. Among many types of statistical methods mentioned in literatures， the Monte Carlo simulation is the most commonly used one. Monte Carlo simulation is often adopted for generating experimental random samples which are then used to evaluate failure probability and probability distributions of system response under the effects of the probabilistic properties of system variables［17-18］. The advantages of this method lie in their easy implementation， satisfactory estimation accuracy and convergence speed independent of problem dimensions， etc. On the contrary， the mainly drawback of Monte Carlo simulation is referred to the huge computational costs for most practical problems. Based on Monte Carlo simulation，BRUYèRE， et al［19］， presented a vectorial dimensioning and tolerancing model for quantitatively analyzing the tolerances. A very few statistical studies have been presented to figure out the probabilistic results of STE and design parameters［20-21］. For example， MAO， et al［20］，proposed a statistical analysis method to evaluate the STE of a mechanical watch movement.

From the above discussions， it can be found that there is a margin in the statistical analysis of the effects of modifications on planetary gear dynamics. Though an analytical tooth modification model for dynamic analysis of spur planetary gear train was proposed by BAHK， et al［6］，this model still belongs to deterministic study since the presence of uncertainties in tooth modification parameters were not taken into account. In order to achieve satisfactory dynamic performances and ensure transmission without failure， it is necessary to analyze and quantify uncertain characteristics of the system dynamic responses influenced by variations of manufacturing and installing errors. The present work has a different perspective in that it aims to explore the effect of tooth micro-geometry modifications on helical planetary gear dynamics with the consideration of uncertainties in tooth modification process. For this purpose， we assume to shift the variation of manufacturing and installing errors to the variation of modification amounts and then analyze the uncertainty of ΔDTE aroused by modification amounts variation. To do so， a nonlinear dynamic model of a helical planetary gear considering tooth modification is established firstly. With the deterministic model， the dynamic loads of the gear system can be calculated and further used to compute the DTE curves. And then the response surface method combining with the central composite design is applied to develop a fitted regression model about tooth modification parameters and system ΔDTEs. Finally， an uncertainty analysis is carried out to predict the probability distributions of limit state functions and failure probability of tooth modifications based on Monte Carlo simulation. The statistical results can provide useful information for gear designers to estimate the effects of tooth micro-geometry modifications on system dynamic performances with consideration of parameter uncertainties in tooth modification process.

2 Deterministic Modification Modeling and Dynamic Analysis

In this section， a three dimensional lumped-parameter dynamic model of a helical planetary gear train developed by KAHRAMAN［22］is adopted as the basic model. This basic model is then augmented with a tooth modification model to take account in the effect of micro-geometry modifications.

2.1 Dynamic model with consideration for tooth modifications

The schematic of the helical planetary gear dynamic model is demonstrated in Fig. 1.

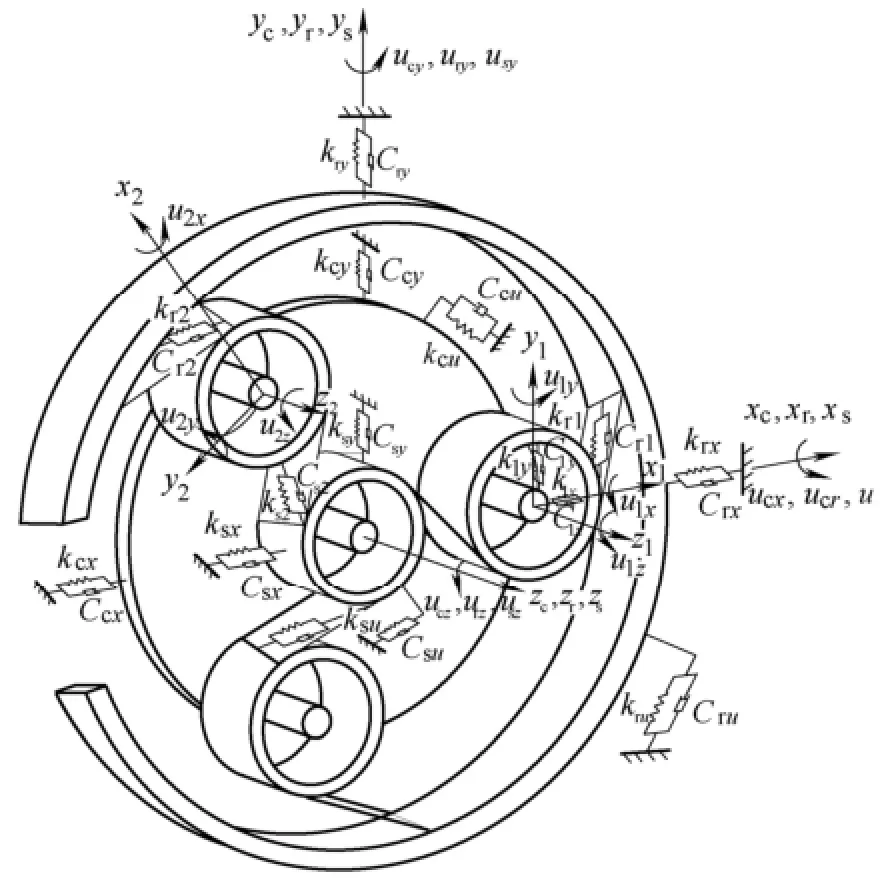
Fig. 1. Dynamic model of a helical planetary gear train

In Fig. 1， xj， yj， zjand ujx， ujy，ujz（ j=s， c， r， n） denote the three translational and three rotational deflections of each component where the subscript “s”， “c”， “r” and “n” stand for the sun gear， the carrier， the ring gear and the nth planet gear， respectively. kjiand cji（ j=s， c， r， p； i=x， y， u）represents the bearing stiffness and damping of corresponding component in related direction. ksn， krnand csn， crndenote the mesh stiffness and damping of the nth sun-planet（s-p） and ring-planet（r-p） gear pairs， respectively.

As addressed by KAHRAMAN in Ref. ［22］， the governing equation of motion for a helical planetary geartransmission system with Npplanets can be expressed as

where m， c and k represent the governing mass matrix，damping matrix and stiffness matrix， respectively； q and f are the general coordinates and excitations. The general coordinates can be written in the matrix format as

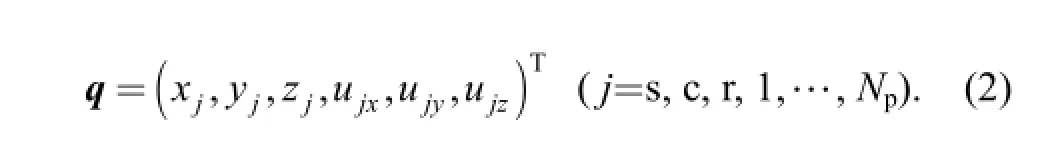
The stiffness matrix k can be further expressed as

where kbis a diagonal matrix of bearing stiffness； km（q， t） is mesh stiffness matrix consisting of nonlinear time-varying stiffness of sun-planet and ring-planet gear pairs. The uniform stiffness expression for the sun-planet and ring-planet gear pairs is

Note that unavoidable manufacturing and installing errors of gears， shafts and the housing as well as deflections of gears and supporting structures subject to load may alter gear transmission errors， which in turn increases the vibration and noise of the transmission system. For the purpose of vibration and noise suppression， tooth microgeometry modifications are often employed to eliminate， or at least decrease the fluctuation of dynamic transmission errors. In order to take account of the tooth modification in the above dynamic model， an additional excitation vector e（q， t） will be derived and added to the excitation vector f in Eq. （1）.

Fig. 2 shows a representative sketch of tooth helix angle modification function and tooth profile crowning modification function. Herein， CHβdenotes helix angle amount， b is face width， LAEis tooth depth， Cαdenotes profile crowning amount.

Fig. 2. Modification scheme

Assume the mesh deflection of the sun-planet pair and the ring-planet pair after micro-geometry modifications is

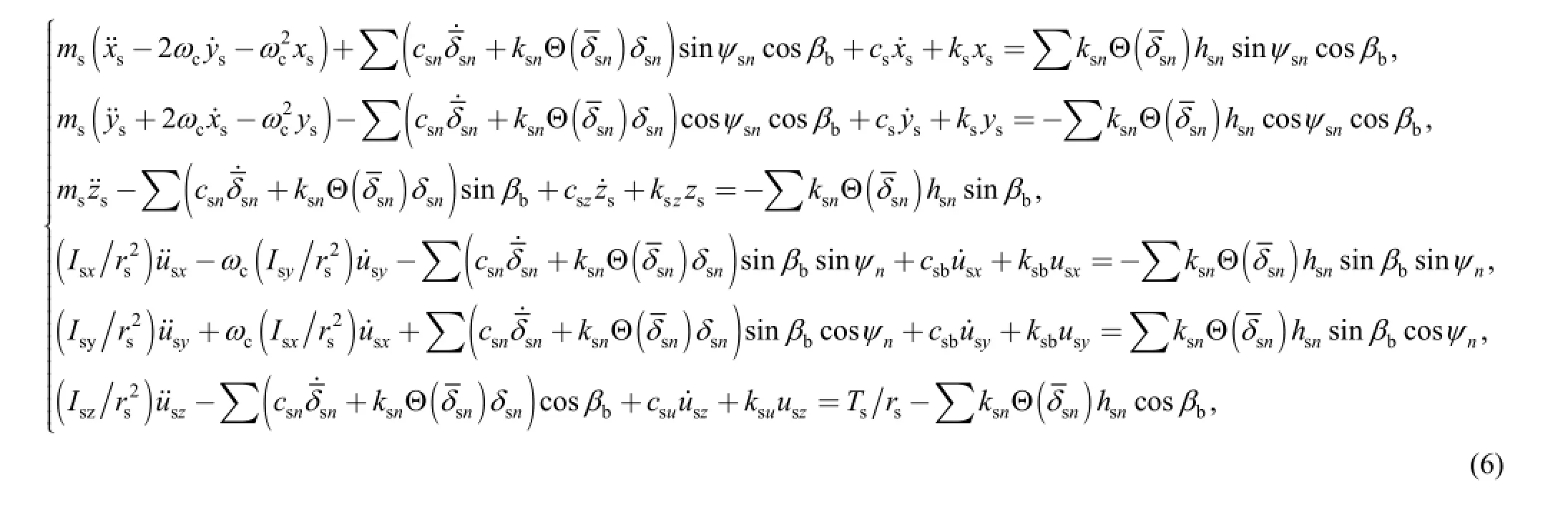
where ωcis rotation speed of the carrier； msis mass of the sun gear； βbishelical angle of the base circle； ψsn= αts+ψnwith ψnbeing the position angle of the nth planet gear and αtsbeing meshing angle of sun-planet gear pair at the end face； Isj（ j=x， y， z） is inertia of the sun gear in related direction measured in body-fixed reference frame； rsis radius of pitch circle of the sun gear； Tsis the external torque applying on the sun gear.

The right side of the Eq. （6） can be further expressed in the matrix form as

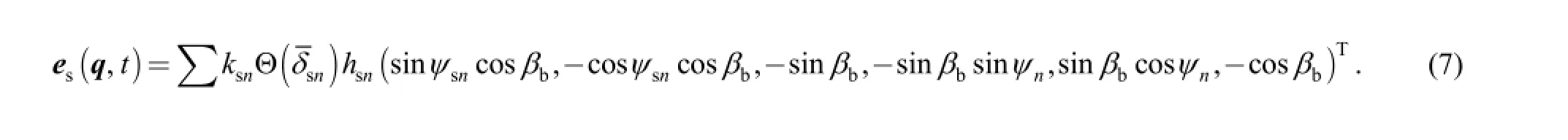
The physical interpretation for the above equation is the additional excitations aroused from tooth modifications.

Similarly， the additional excitations for the ring gear and planet gear can be formulated as

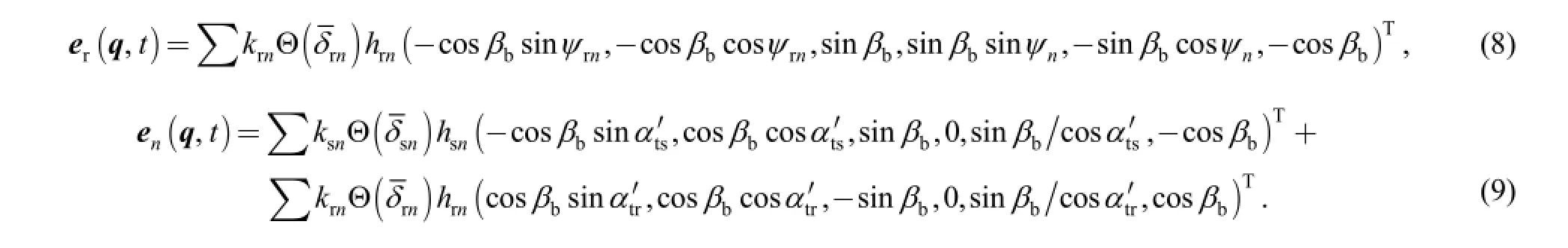
By assembling the additional excitations of each component， one can derive the global additional excitation matrix exerted by tooth modifications as

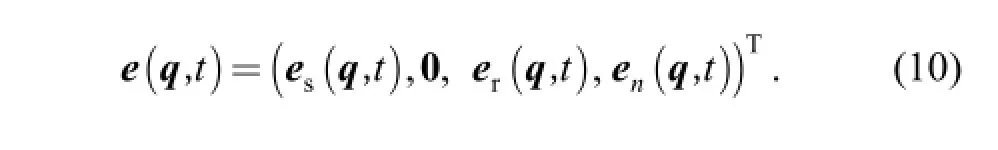
By introducing the additional excitations e（q， t） into the system's dynamic equations， Eq. （1） changes to

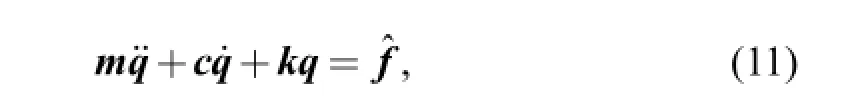
Eq. （11） is a second order differential equation set with variable coefficients whose dimension is （6Np+18）. For this kind of equation， it is very hard to obtain an analytical solution for the steady state dynamic responses. Therefore，a numerical method of variable step size forth order Runge-Kutta method is adopted here to compute the dynamic transmission errors and mesh forces of the helical planetary gears. For this purpose， the equations of motion as shown in Eq. （11） must be nondimensionalized firstly and is expressed in the matrix form as

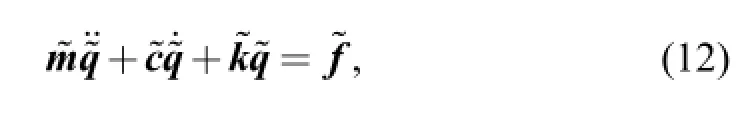
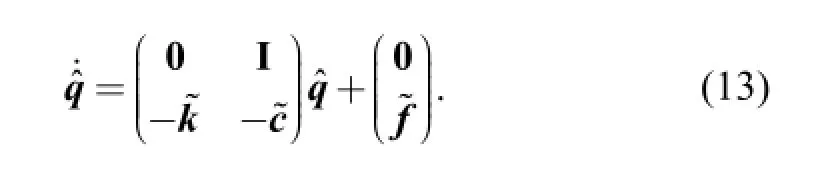
With the above transformation， the equations of motion of the system turns into a first order differential equation set with variable coefficients， which can be solved with variable step size fourth order Runge-Kutta method through numerical integration.

2.2 Dynamic analysis and discussions

The following will investigate the dynamic responses of an example helical planetary gear system with and without tooth modifications. This example system of helical planetary gear set is the lower-speed-stage transmission in a MW wind turbine gearbox. The major design variables of the example system are listed in Table 1.

Table 1. Design variables of the example system

For such a helical planetary gear train， a comprehensive tooth modification strategy was proposed with the aim of achieving minimal STE fluctuation by Guo， et al［23］. The study indicates that an amount of 88 μm for helical angle modification and an amount of 56 μm for profile crowning modification on the sun gear can effectively eliminate the STE fluctuation. For clarity， Fig. 3 demonstrates the modification scheme of the sun gear［23］.

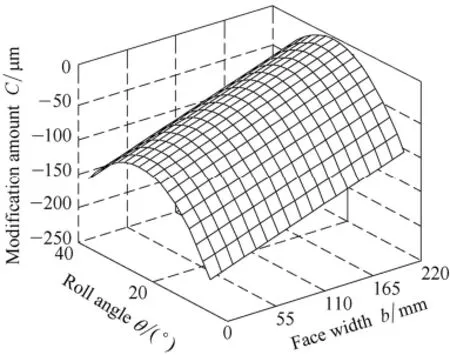
Fig. 3. Modification view of the sun gear

Based on the nonlinear dynamic model proposed in section 2.1， the steady state dynamic responses of the example system can be numerically computed through variable step size fourth order Runge-Kutta method. By solving the first order differential equation set of Eq. （13），the dimensionless dynamic displacementscan be obtained. This dimensionless dynamic displacementare then transformed back to the physical dynamic displacements q by multiplying the nondimensional coefficients. The dynamic displacement along the line of action of the sun-planet pair can be formulated as

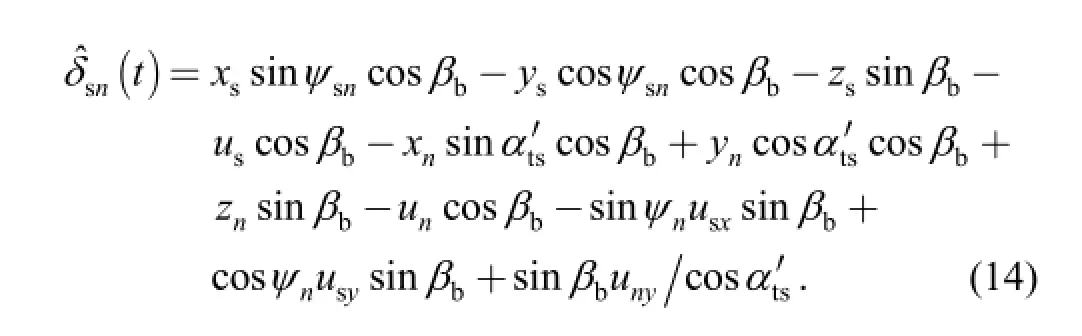
Eq. （14） gives the dynamic transmission error of the sun-planet gear pair in a mesh cycle. With this equation， the dynamic transmission error of the sun-planet gear pair can be computed either in time domain or frequency domain.

Furthermore， by multiplying the dynamic transmission error with time-varying mesh stiffness， the dynamic mesh force of the sun-planet gear pair can be computed through the following equation:

with the time-varying mesh stiffness being expressed as

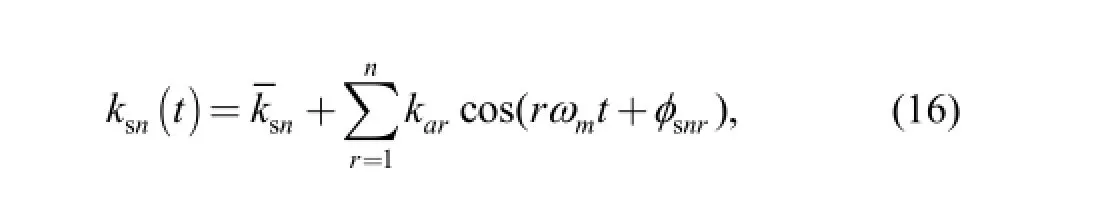
For the sake of simplicity， the following will only explore the dynamic transmission errors and dynamic mesh force of the sun-planet 1（s-p1） gear pair to demonstrate the deterministic dynamic analysis.

Based on Eq. （14） and Eq. （15）， one can use the fast Fourier transformation to compute the dynamic responses in frequency domain. Fig. 4 illustrate the first three orders harmonic components of the dynamic transmission error and dynamic mesh force of the s-p1gear pair without considering the effects of tooth modifications.

As observed from Fig. 4， the dynamic transmission error and dynamic mesh force share the same resonance peaks. The first resonance peak appears at 2213 Hz followed by three minor resonance peaks locating at 2857 Hz， 3018 Hz and 4087 Hz. Meanwhile， it can be observed that the amplitudes of the first order harmonic component of the dynamic responses are much higher than those of the other two orders harmonic components. This indicates that the first order resonance contributes a lot to the system's overall dynamics， thus should be paid more attention during the design stage.

Fig. 4. Dynamic responses of the s-p1gear pair without tooth modifications

Since the dynamic mesh force can be regarded as an excitation result from dynamic transmission error as shown in Eq. （15）， one may naturally think of reducing the dynamic mesh force and dynamic transmission error through tooth modifications. Bearing with this thought， a comprehensive tooth modification strategy shown in Fig. 3 is adopted here to reduce the dynamic responses of the example helical planetary gear system. Fig. 5 gives the first three orders of harmonic dynamic transmission error and dynamic mesh force of the s-p1gear pair after considering the influence of tooth modifications.

By comparing Fig. 5 with Fig. 4， it can be clearly observed that the dynamic responses of the s-p1gear pair decrease dramatically with the proposed micro-geometry modifications. To be specific， the amplitudes of the first three orders of the dynamic transmission error decrease from 26.73 μm， 5.86 μm and 2.26 μm to 0.64 μm， 0.26 μm and 0.07 μm at the first resonance peak. The amount of peak-to-peak variation for the first order harmonic DTE is 26.6 μm before tooth modifications while turns to 0.57 μm after tooth modifications. Meanwhile， the amplitudes of first three orders of dynamic mesh force decrease from103 240 N， 22 611.1 N and 7939.6 N to 2489 N， 1022.4 N and 282.7 N at the first resonance peak. The amplitudes of the first three orders dynamic force are decreased by 97.6%，95.4% and 96.4%， respectively. The amplitudes reduction of dynamic transmission error and mesh force manifests that the proposed tooth modification strategy can effectively improve the dynamic performance of the s-p1gear pair.

Fig. 5. Dynamic responses of the s-p1gear pair with tooth modifications

3 Statistical Modification Modeling and Uncertainty Analysis

As seen from section 2， the deterministic dynamic model with inclusion of modifications is quite complicated. The motion of equations of the system is a large dimensional nonlinear differential equations， which makes the solution for dynamic responses very difficult. The calculation of ΔDTEs requires heavy computational expense with high possibility of failure due to ill-conditioned sensitivity matrices. Therefore， a simple and cost-efficient mathematical fitted regression model based on response surface method to substitute for the actual nonlinear dynamic model is proposed in this section.

3.1 Fitted regression model

Considering the complex nonlinearity of ΔDTEs， it may be appropriate to adopt a second-order polynomial expression to describe the relationship between the modification parameters and the ΔDTEs. The structure of response surface function for modification parameters and ΔDTEs can be expressed as

where β denotes the regression coefficients to be determined by least squares estimation； xirepresents the main effect of parameter i and xixjgives the interaction effect between two parameters.

Our previous research indicates that a combining helix angle modification and profile crowning modification on the sun gear can effectively eliminate the static transmission error fluctuation（ΔSTE） of s-p1 pair［23］. Therefore， the helix angle modification amount x1， the profile crowning modification amount x2are chosen as the design variables.

The central composite design is adopted for fitting the second-order model shown in Eq. （18）. As known， a central composite design consists of 2kfactorial， 2k axis runs and at least one center runs. This means that it only needs（2k+2k+1） samples. Herein， the number of random variables k=2. In the central composite design， the distance between the axis points and the center point α should be reasonably selected to ensure all points are equidistance apart from the center point. Such a selection helps to achieve a same standard deviation when predict the system response with the RSM function. The distance α can be calculated throughwhere nfis the number of corner points and is decided by the number of random variables and the factor levels.

According to the gear quality grades and tolerance range，the exploration region to fit the second-order model is that helix angle modification amount is from 81.6 μm to 94.4 μm； profile crowning modification amount is from 49.6 μm to 62.4 μm. To simplify the calculation， independent variables are coded to the usual （-1， 1） interval， and the level of factors are shown in Table 2. Table 2 also gives the central composite design samples and the results of the ΔDTEs calculated by the nonlinear dynamic model proposed in section 2. Herein， the variables y1， y2and y3denote the first three orders of harmonic ΔDTEs， respectively.

Using the orthogonal experimental results from central composite design samples， the fitted regression expressions of ΔDTEs can be formulated through the following matrix notation:

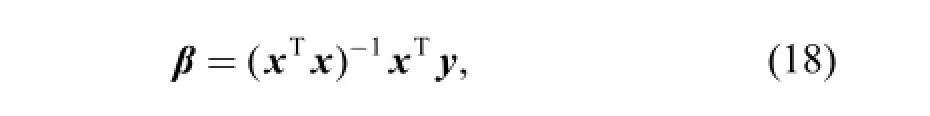
where β is the least squares estimator， x is the center composite sample points， y is the corresponding central composite responses. The three symbols of β， x and y can be further expressed in the matrix forms as follows:

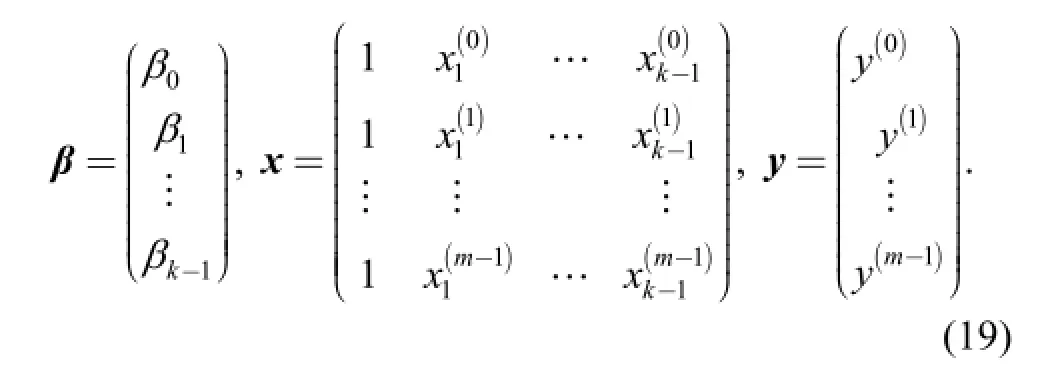
Substituting the central composite design sample values and the results of ΔDTEs into Eq. （19） yields the fitted regression expressions about ΔDTEs and modification variables. The response surface functions of ΔDTEs excited by the first three orders harmonic of modification parameters are obtained and listed in Table 3.

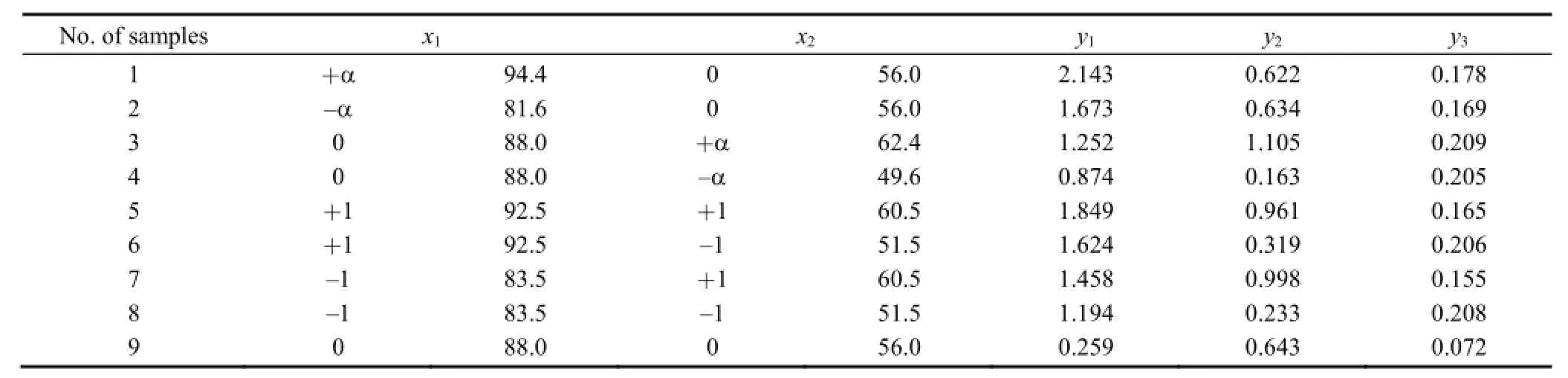
Table 2. Random variables level table and regression results of ΔDTEs

Table 3. Response surface functions of ΔDTEs

The usefulness of the obtained regression models needs to be evaluated with coefficient of multiple determination R2. If the coefficient of multiple determination R2approaches 1， it indicates that the obtained response surface function can replace the actual implicit limit state function without causing too much deviation. The coefficient of multiple determination R2can be calculated through the following formula:

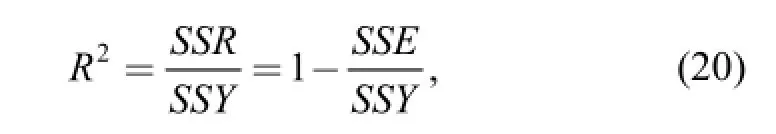
where SSR is the sum of squares of deviations of the response estimated value and response mean； SSY is the sum of squares of deviations of response value and response mean； SSE is the sum of squares of deviations of response value and response estimated value.

With Eq. （20）， the coefficient of multiple determination R2can be calculated and the results are listed in Table 3. From this table， it can be found that the coefficients R2of the three response surface models for three harmonic ΔDTEs are 0.997 0， 0.998 7 and 0.912 9， respectively. Obviously， the coefficients R2of the response surface models for the first two orders harmonic ΔDTEs are very close to the value of 1. Meanwhile， the coefficient R2of the response surface model for the third order harmonic ΔDTE also approaches 1 with a high value of 0.9129. This means that the obtained fitted regression models explain approximately 99.7%， 99.87% and 91.29% of the observed variability of the quantitative relationships between tooth modifications and system ΔDTEs. Thus， the usefulness of the proposed fitted regression models are confirmed， which can be further used for uncertainty analysis in the following subsection.

3.2 Uncertainty analysis with MCS

As aforementioned， the inevitable manufacturing and installing errors in real engineering situations will bring uncertainties to the calculation of DTEs（or ΔDTEs）. Therefore， an uncertainty analysis is needed to make sure the proposed modifications based on deterministic model can achieve desired design expectations. To do so， we assume that those unavoidable errors of the gear system can be shifted to the modification amounts， making the two modification amounts x1and x2become random variables. Then the uncertainty of ΔDTEs caused by errors can be regarded as similar uncertain events aroused from random variations of modification amounts， which can be analyzed through statistical analysis to predict the probability distribution and failure probability.

Before carried out an uncertainty analysis， one needs to determine the random variables distribution type（e.g.，normal， lognormal， uniform， etc.）， along with the mean value μ and standard deviation σ of each geometrical deviation. However， to determine random variables probability distribution type is not easy. In some specific instances， such as an industrial product or process，considerable amount of experiments and experience are required to determine each distribution type. Here we advocate a normal distribution type for ΔDTE according to previous studies. In order to control the vibration intensity of a gear system， the maximum ΔDTE is recommended not to exceed 4 μm. Therefore， the mean values μ of the first three orders of harmonic ΔDTEs are designated as 4 μm， 2 μm and 1 μm， respectively， while the standard deviation σis set as 0.5 μm. Using the same rule， we assign a normal distribution for modification parameters x1and x2， with mean values of 88 μm and 56 μm， respectively and a standard deviation of 4.5 μm.

With the determined normal distributions of ΔDTE and modification parameters x1and x2， a set of random samples ofcan be generated by Monte Carlo simulation. To ensure the approximation accuracy of Monte Carlo simulation， a large number of samples are needed. In the present Monte Carlo simulation，the number of samples is chosen as a large size of 90 000. However， it should be noted that it is extremely time-consuming to run such a large number of deterministic dynamic simulations（as described in section 1） for tooth modification variations. This drives the authors to propose a computational efficient method to deal with the problem. Bearing with this thought， a combining methodology of response surface method-based Monte Carlo simulation is proposed in this paper. The basic idea of the methodology is replacing the time-consuming dynamic model with fitted regression model to calculate the ΔDTEs yiunder random modification variables samplesThen we can define the limit state function as

With Eq. （21）， the limit state functions of the first three orders harmonic ΔDTEs can be calculated and their histograms as well as their means value and standard deviations are demonstrated in Fig. 6.

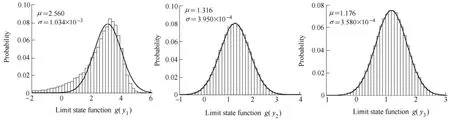
Fig. 6. Histograms of g（y） through Monte Carlo simulation

As can be observed from Fig. 6， the distribution of the limit state function g（y1） is no longer a normal distribution while the limit state functions g（y2） and g（y3） still keep the normal distribution status. This is quite interesting in that it implies a normal distribution samples of modification variables is not bounded to yield a normal distribution of ΔDTEs. And more precisely and specifically， if the error deviations in a planetary gear system is normal distributed，the dynamic transmission error fluctuations do not obey the normal distribution law. This may be explained by the strong nonlinearity of the gear transmission system. Other information can also be extracted from the above figures. For example， the mean values of three functions is 2.560 μm， 1.316 μm and 1.176 μm， respectively； the standard deviations of the three functions are very small with magnitudes of 10-3. The following will discuss the failure probability of the modifications by defining Pfas

Since Monte Carlo simulation is based on a very simple thinking of Large Number Law， the sample means can approximately replace the mathematical expectation of the failure indicates function. And the failure probability estimates can expressed as

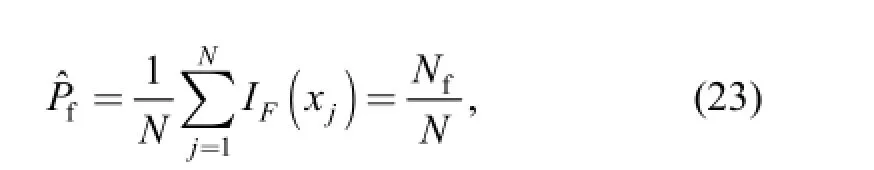
Fig. 7 gives the cumulative distribution functions of g（y）.

Fig. 7. Cumulative distribution functions

From Fig. 7 it can be clearly seen that the failure probability of the three limit state functions are 5.67%， 1.42% and 1.17%， respectively. This indicates that with the proposed deterministic modification amounts of x1=88 μm and x2=56 μm， there is a percentage of 5.67% ΔDTE of the first order harmonic exceeds fluctuation threshold value when take account in the random errors. Meanwhile， there are percentages of 1.42% and 1.17% ΔDTEs exceed threshold values for the second and the third orders of harmonics. And the modification amounts are determined by minimal ΔSTE， this means that a deterministic modification amount is not definitely to achieve an optimal result for both static and dynamic transmission error fluctuation reduction simultaneously.

For a statistical analysis， it is also necessary to carry out variance analysis of failure probability estimation to check its convergence. If the order of magnitude for variance coefficient of failure probability reaches 10-2， it means the Monte Carlo random samples are sufficiently to guarantee failure probability satisfy the convergence condition.

The estimated variance of failure probability is

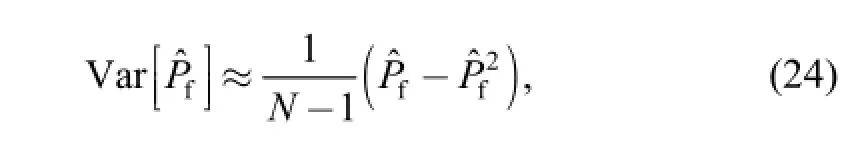
and the variation coefficientis

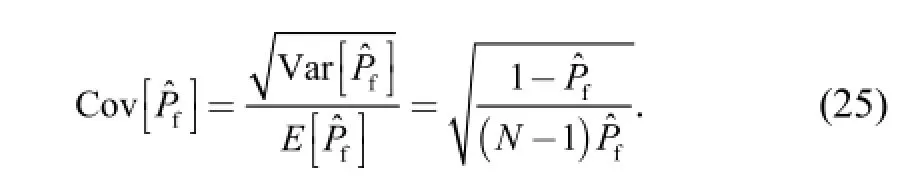
Further computation through Monte Carlo simulation revealed that the variation coefficients of failure probability are 0.018 2， 0.027 7 and 0.030 7. Since the order of magnitude for the three variance coefficients all reach 10-2，it means that the samples for statistical analysis are sufficient enough to guarantee failure probability satisfy the convergence condition.

4 Conclusions

（1） An deterministic analytical dynamic model with consideration of tooth modification for helical planetary gears is developed， based on which the influence of tooth modifications on gear dynamic behaviors are analyzed. The numerical simulation results proves that a proposed combining helix angle and profile crowing modifications can effectively decrease the dynamic responses of the gear system.

（2） A fitted regression model based on the response surface method and central composite design is presented to quantify the relationship between tooth modification amounts and dynamic transmission error fluctuations. The effectiveness of the obtained fitted regression model is validated and thus can be used to predict the dynamic transmission error fluctuation of a helical planetary gear set in a quick yet accurate manner.

（3） The uncertainty of the effects of tooth modification variations on ΔDTEs of planetary gears is analyzed through a statistical model. By combining the response surface method and Monte Carlo simulation， the probability distribution and failure probability of the defined limit state functions are predicted.

（4） The statistical analysis indicates that the system ΔDTEs do not obey the normal distributions even though the distribution of modification variables（or the errors） is normal. In addition， the deterministic modification amounts will not definitely achieve an optimal result for both static and dynamic transmission error fluctuation reduction simultaneously. This should be paid enough attention during the design stage of a gear transmission.

［1］ BONORI G， BARBIERI M， PELLICANO F. Optimum profile modifications of spur gears by means of genetic algorithms［J］. Journal of Sound and Vibration， 2008， 313（3）: 603-616.

［2］ JAO Huang K， WEI Su H. Approaches to parametric element constructions and dynamic analyses of spur/helical gears including modifications and undercutting［J］. Finite Elements in Analysis and Design， 2010， 46（12）: 1106-1113.

［3］ LI S. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors， assembly errors and tooth modifications［J］. Mechanism and Machine Theory，2007， 42（1）: 88-114.

［4］ GUILBAULT R， GOSSELIN C， CLOUTIER L. Helical gears，effects of tooth deviations and tooth modifications on load sharing and fillet stresses［J］. Journal of Mechanical Design， 2006， 128（2）: 444-456.

［5］ BRUYèRE J， VELEX P. A simplified multi-objective analysis of optimum profile modifications in spur and helical gears［J］. Mechanism and Machine Theory， 2014， 80: 70-83.

［6］ BAHK C J， PARKER R G. Analytical investigation of tooth profile modification effects on planetary gear dynamics［J］. Mechanism and Machine Theory， 2013， 70: 298-319.

［7］ BAHK C J， PARKER R G. A study on planetary gear dynamics with tooth profile modification［J］. ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference， American Society of Mechanical Engineers， 2011: 365-377.

［8］ KAHRAMAN A， BLANKENSHIP G W. Effect of involute contact ratio on spur gear dynamics［J］. Journal of Mechanical Design， 1999，121（1）: 112-118.

［9］ TAMMINANA V K， KAHRAMAN A， VIJAYAKAR S. A study of the relationship between the dynamic factors and the dynamic transmission error of spur gear pairs［J］. Journal of Mechanical Design， 2007， 129（1）: 75-84.

［10］ HOTAIT M A， KAHRAMAN A. Experiments on the relationship between the dynamic transmission error and the dynamic stress factor of spur gear pairs［J］. Mechanism and Machine Theory， 2013，70: 116-128.

［11］ MYERS R H， VINING G G， GIOVANNITTI-JENSEN A， et al. Variance dispersion properties of second-order response surface designs［J］. J. Quality Tech， 1992， 24: 1-11.

［12］ FARAVELLI L. Response surface approach for reliability analysis［J］. J Eng Mech， ASCE， 1989， 115（12）: 2763-2781.

［13］ RAJASHEKHAR M R， ELLINGWOOD B R. A new look at the response surface approach for reliability analysis［J］. Structural Safety， 1993， 12（3）: 205-220.

［14］ GUAN X L， MELCHERS R E. Effect of response surface parameter variation on structural reliability estimates［J］. Structural Safety， 2001， 23（4）: 429-444.

［15］ ANDERSON-COOK C M， BORROR C M， MONTGOMERY D C. Response surface design evaluation and comparison［J］. Journal of Statistical Planning and Inference， 2009， 139（2）: 629-641.

［16］ PARK C IL. Multi-objective optimization of the tooth surface in helical gears using design of experiment and the response surface method［J］. Journal of Mechanical Science and Technology， 2010，24（3）: 823-829.

［17］ SKOWRONSKI V J， TURNER J U. Using Monte-Carlo variance reduction in statistical tolerance synthesis［J］. Computer-Aided Design， 1997， 29（1）: 63-69.

［18］ FANG S E， REN W X， PERERA R. A stochastic model updating method for parameter variability quantification based on response surface models and Monte Carlo simulation［J］. Mechanical Systems and Signal Processing， 2012， 33: 83-96.

［19］ BRUYèRE J， DANTAN J Y， BIGOT R， et al. Statistical tolerance analysis of bevel gear by tooth contact analysis and Monte Carlo simulation［J］. Mechanism and Machine Theory， 2007， 42（10）: 1326-1351.

［20］ MAO J， CAO Y L， YANG J X. A transmission error analysis method using Monte Carlo simulation［J］. Advanced Science Letters，2011， 4（6-7）: 2474-2477.

［21］ DRIOT N， PERRET-LIAUDEt J. Variability of modal behavior in terms of critical speeds of a gear pair due to manufacturing errors and shaft misalignments［J］. Journal of Sound and Vibration， 2006，292（3）: 824-843.

［22］ KAHRAMAN A. Planetary gear train dynamics［J］. Journal of Mechanical Design， 1994， 116（3）: 713-720.

［23］ GUO F， ZHANG J. Analysis of the mesh characteristic and study on the modification reliability for planetary gear train with flexible carrier［J］. Journal of Mechanical Transmission， 2014， 38（9）: 1-4.（in Chinese）

Biographical notes

ZHANG Jun， born in 1981， is currently a professor and a MSc candidate supervisor at School of Mechanical Engineering， Anhui University， China. He received his PhD degree in mechanical design and theory from Tianjin University， China， in 2007. His research interests include mechanisms and machinery dynamics.

Tel: +86-188-555-21039； E-mail: zhang_jun@tju.edu.cn

GUO Fan， born in 1988， is currently a master candidate at School of Mechanical Engineering， Anhui University， China. She received her bachelor degree in mechatronics from Anhui University of Technology， China， in 2012. Her research interest is gear transmission.

E-mail: guofan197@163.com

10.3901/CJME.2015.0610.079， available online at www.springerlink.com； www.cjmenet.com； www.cjme.com.cn

* Corresponding author. E-mail: zhang_jun@tju.edu.cn

Supported by National Natural Science Foundation of China（Grant No. 51375013）， and Anhui Provincial Natural Science Foundation of China（Grant No. 1208085ME64）

© Chinese Mechanical Engineering Society and Springer-Verlag Berlin Heidelberg 2015

December 25， 2014； revised June 8， 2015； accepted June 10， 2015