铸型对镁合金铸造过程温度分布的影响

胡瑞霞, 袁训锋, 杨 燕, 刘宝盈, 李 英, 刘 院, 郝 强

( 商洛学院, 陕西商洛 726000 )

铸型对镁合金铸造过程温度分布的影响

胡瑞霞, 袁训锋, 杨 燕, 刘宝盈, 李 英, 刘 院, 郝 强

( 商洛学院, 陕西商洛 726000 )

采用直接差分法求解热传导方程，对镁合金铸造过程进行模拟，研究了铸型条件对温度分布和铸件质量的影响。结果表明：砂型铸造条件下，铸型导热系数小，铸件凝固速率慢，铸件铸型界面温度值突变小；金属型铸造条件下，铸型导热系数大，铸件凝固速率快，铸件铸型界面温度值突变大。在实际铸造工艺中，需选择合适导热系数的材料制作铸型，从而在避免较大热变形和热裂现象的同时提高铸造速度。

镁合金；铸造过程；温度分布；铸型

数值模拟技术研究铸件凝固过程，具有成本低、周期短的优势。自20世纪60年代提出以来，迅速成为铸造学科研究的热点。Forsund首次将有限差分法应用到传热计算中，开创了应用计算机数值模拟技术研究铸件凝固过程的先河［1］。随着计算机技术和数值方法的发展，凝固过程数值模拟逐渐从探索凝固规律、丰富凝固理论，发展到与工程问题相结合指导生产实践。

目前，众多学者采用PROCAST［2］、AutoCAD［3］、ANSYS［4-8］等商业软件对铸件凝固过程的温度场进行模拟研究，获得部分铸件凝固规律，为铸件工艺设计提供参考。但这些基于商业软件的温度场模拟研究，无法揭示凝固过程中的部分物理本质。赵鑫［9］、陈玲［10］、安晓卫［11］等采用有限元和有限差分方法求解温度场，在分析铸件和铸型间界面传热系数对铸件凝固温度场影响的基础上，提出了处理界面传热问题的有效方法。袁训锋［12］等采用直接差分法求解热传导方程，运用C++语言编写模拟程序，研究了铸件/铸型热阻对温度分布及拐角处凝固速率的影响。

本文在文献［12-13］基础上，对镁合金铸造过程进行模拟，探讨了砂型、金属型两种铸型条件下的温度分布情况，绘制了计算区域中心和中心轴位置的温度随时间变化曲线。

1　铸件计算模型

1.1T型铸件模型

T型铸件模型如图1所示，铸件结构尺寸如表1所示。

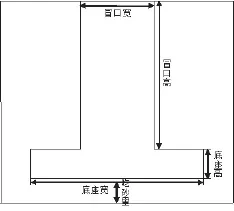
图1　T型铸件模型图

 表1 T型铸件模型结构尺寸图　　　　　　　　　　　cm

1.2参数值的选取

铸造外部条件如表2所示，材料AZ91合金和铸型的热物性参数如表3所示。

表2　铸造的外部条件

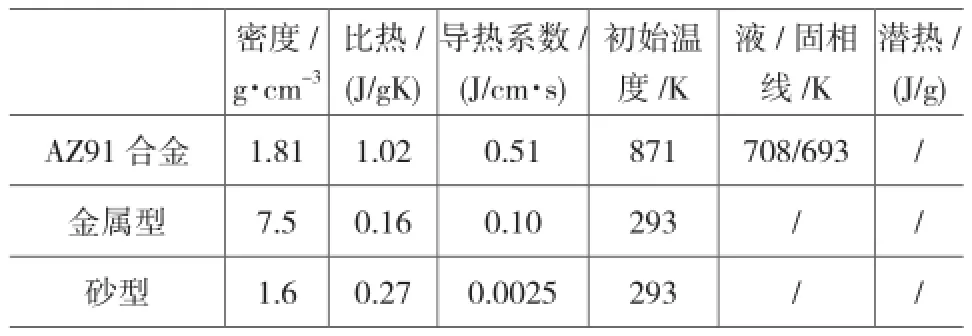
表3　热物性参数

1.3热传导微分方程

二维传热问题的热传导微分方程为：

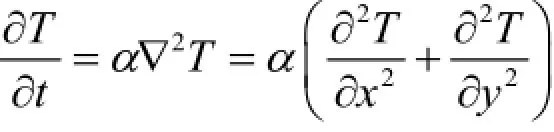
其中，热扩散系数α=λ/ρcp，λ为导热系数，ρ为密度，cp为比热，T为温度。

2　温度场模拟程序的实现

2.1网格剖分

网格大小设定为1 cm×1 cm，总网格数为82×82，离散化后的计算区域如图2所示。

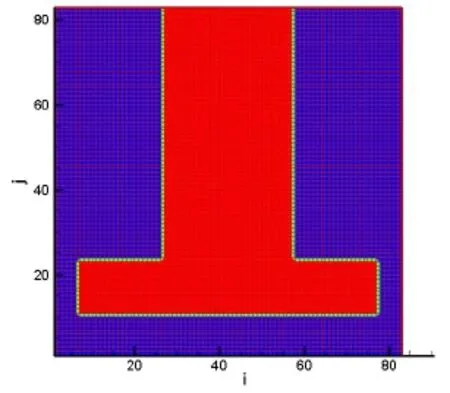
图2　离散化计算区域示意图

2.2程序实现过程

将热量守恒直接应用到差分单元上，根据传入热量等于热量积蓄，建立节点方程：

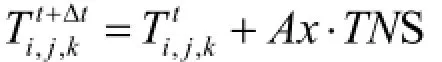
3　结果与分析

3.1镁合金砂型铸造过程中不同时刻的温度分布

镁合金砂型铸造过程中不同时刻温度分布如图3所示。从图中可以看出，在凝固初期，铸件内部大部分单元颜色为红色（图中心深色部分），温度值接近金属液的初始温度，铸型内部大部分单元颜色为蓝色（周边深色部分），温度值接近环境温度；在内部区域，热量通过铸件/铸型界面向铸型传递，在铸件/铸型界面前沿形成热扩散层；在冒口区域，热量通过铸件/空气界面向外部环境传递，由于铸件/空气界面热阻较小，热量传递快，迅速形成不同颜色的热扩散层“阶梯”，如图3.a所示。随着时间的推移，铸件/铸型界面前沿的热扩散层增厚，冒口区域的热扩散层“阶梯”以平面形式向内部推进，铸件冒口区域各单元颜色逐渐变浅先凝固并将铸件底座部分的金属液封闭起来，形成封闭的液相区，如图3.b、c所示。到达凝固后期，铸件底座部分颜色逐渐变浅，从液相向固相转变最后凝固，如图3.d所示。

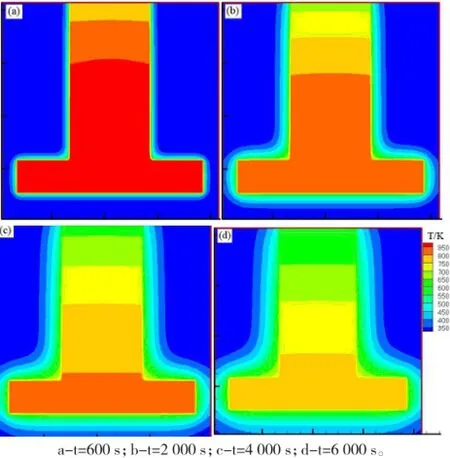
图3　镁合金砂型铸造过程中不同时刻温度分布

3.2镁合金金属型铸造过程中不同时刻的温度分布

镁合金金属型铸造过程中不同时刻温度分布如图4所示。从图中可以看出，热量通过铸件/铸型、铸件/空气界面分别向铸型和外部环境传递，由于金属铸型与砂型相比，具有更好的热传导能力，在冒口和底座区域均迅速形成不同颜色的热扩散层“阶梯”，但在铸件/铸型界面前沿未形成热扩散层，如图4.a所示。随着时间的推移，在底座下沿中心和底座与冒口的拐角位置形成热扩散层并不断扩展，底座区域不同颜色的热扩散层“阶梯”消失，冒口区域的热扩散层“阶梯”以球面形式向内部推进，铸件冒口区域各单元颜色逐渐变浅先凝固并将铸件底座部分的金属液封闭起来，形成封闭的液相区，如图4.b、c所示。到达凝固后期，铸件底座部分颜色逐渐变浅，从液相向固相转变最后凝固，整个铸型底部区域散热效果差，颜色深温度高，如图4.d所示。

3.3砂型和金属型铸造温度场分布定量分析

为了定量分析镁合金砂型和金属型铸造过程中的温度场分布情况，绘制了计算区域中心和中心轴位置的温度随时间变化曲线。图5为不同时刻横坐标i=41位置温度随纵向网格数的变化关系。从图中可以看出，在某时刻横坐标i=41位置，随着纵向网格数增加，首先经过底座下端的铸型，温度升高；再经过铸件铸型界面，温度发生急剧升高进入铸件；最后向冒口靠近，温度逐渐降低。比较图5.a、b发现，金属型底座下端部分的温度曲线比砂型条件下平坦，温度变化缓慢，金属型条件下铸件铸型界面位置的温度值突变比砂型条件下大。

图6为不同时刻纵坐标j=41位置温度随横向网格数的变化关系。从图中可以看出，在某时刻纵坐标j=41位置，温度曲线中间平坦部分对应于铸件部分，两端部分对应于铸型部分。比较图6.a、b发现，在铸型内部，金属型条件下的温度曲线比砂型条件下平坦，这是因为金属型导热系数大，在铸型内部温度变化缓慢，曲线斜率小，砂型导热系数小，在铸型内部温度变化快，曲线斜率大；在铸件铸型界面位置，金属型条件下的温度值突变比砂型条件下大。

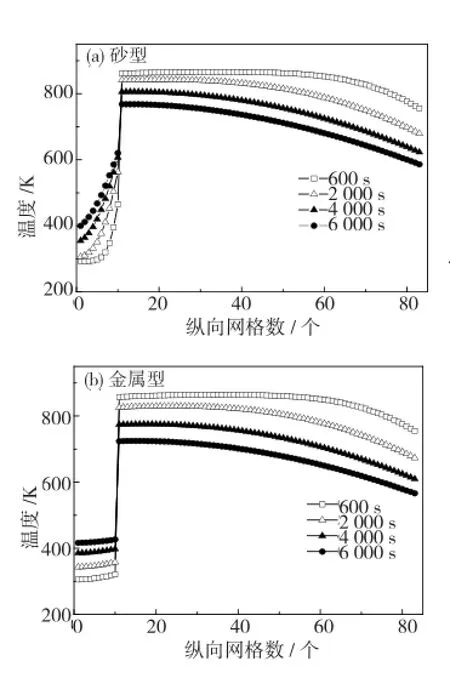
图5　i=41位置温度随纵向网格的变化

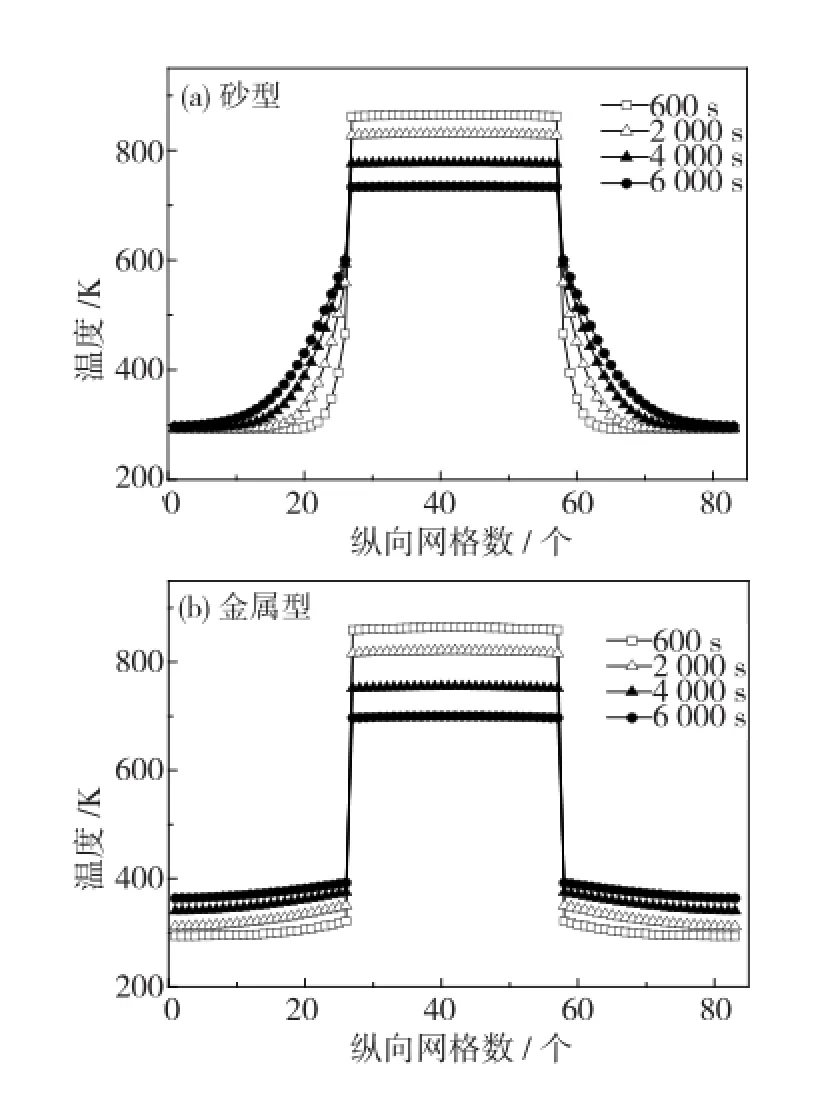
图6　 j=41位置温度随横向网格的变化

图7为计算区域中心位置i=41， j=41温度随时间的变化关系。从图中可以看出，计算区域中心位置的温度随凝固时间增加线性降低。金属型条件下，曲线斜率大，温度下降迅速，铸件凝固速率快；砂型条件下，曲线斜率小，温度下降缓慢，铸件凝固速率慢。

在实际铸造工艺中，一方面铸型宜选择大导热系数的材料加快铸造速度；另一方面，大导热系数材料制作的铸型，在铸件铸型界面上温度值突变大，容易产生较大的热变形和热裂现象。因此，需选择合适导热系数的材料制作铸型，从而在避免较大热变形和热裂现象的同时提高铸造速率。

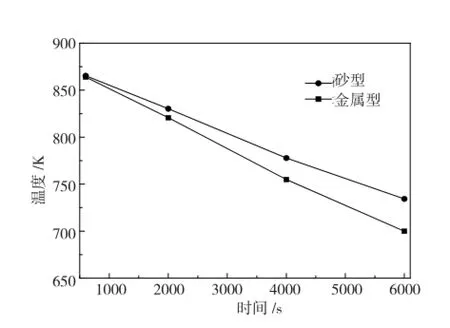
图7　 i=41，j=41位置温度随时间的变化关系

4　　　结论

（1） 在镁合金铸造过程中，铸件空气界面热阻小，散热效果好，冒口区域先凝固，铸件铸型界面热阻大，散热效果差，底座部分后凝固。

（2） 砂型铸造条件下，铸型导热系数小，铸件凝固速率慢，铸件铸型界面温度值突变小，冒口区域的热扩散层“阶梯”以平面形式向内部推进；金属型铸造条件下，铸型导热系数大，铸件凝固速率快，铸件铸型界面温度值突变大，冒口区域的热扩散层“阶梯”以球面形式向内部推进。

（3） 在实际铸造工艺中，需选择合适导热系数的材料制作铸型，从而在避免较大热变形和热裂现象的同时提高铸造速率。

[1] Bastian K M. A Look Back at the 20th Century Casting Process Simulation[J]. Modern Casting, 2000, (12):43-45.

[2] 宁向可, 邹景超, 钱力, 等. 农机犁铧铸件凝固温度场数值模拟[J].铸造技术,2009,30(11): 1393-1395.

[3] 孙建波, 夏春艳, 吕迎, 等. 基于AutoCAD的铸件凝固温度场数值模拟[J].佳木斯大学学报(自然科学版), 2013,31(2): 306-310.

[4] 刘广君. L形镁合金铸件凝固过程温度场的有限元模拟[J].热加工工艺,2011, 40(3):64-68.

[5] 刘艳明, 于静, 张安义.Π型铸件温度场模拟分析[J].山西大同大学学报(自然科学版),2012, 28(5):68-70.

[6] 牛晓武, 赵志龙, 刘林. Al-4%Cu合金铸件凝固过程温度场的数值模拟[J].铸造,2006,55(1):47- 50.

[7] 刘爱敏, 韩衍昭, 王含英.大型铸件凝固过程的温度场数值模拟[J].热加工工艺,2012, 41(15):65-67.

[8] 肖启瑞. 车辆前制动盘三维温度场模拟研究[J].西华大学学报(自然科学版), 2014,33(4):91-93.

[9] 赵鑫, 温泽峰, 金学松. 铸件凝固过程中温度场的数值模拟[J].西南交通大学学报,2006,41(1): 15-19.

[10] 陈玲, 钟蜀津, 殷飞. 铸件和铸型间界面传热系数的试验研究[J].机械设计,2011,28(12):78- 82.

[11] 安晓卫, 王承志, 宋广胜. 铸件凝固温度场有限元分析中界面热阻的处理[J].计算力学学报,2005,22(1): 100-103.

[12] Yuan X F, Hu R X, Li Y, et al. Simulation of Temperature Field in the Solidification Process of Cast[J]. Advanced Materials Research, 2015, 1088: 834-837.

[13] 李东南,汪先明. 铸型冷却速度对半固态镁合金浆料凝固组织的影响[J]. 中国铸造装备与技术,2005(4):34-36.

Infuence of Mould on Temperature Distribution in Casting Process of Magnesium Alloy

HU RuiXia， YUAN XunFeng， YANG Yan， LIU BaoYing， LI Ying， LIU Yuan， HAO Qiang
（Shangluo University， Shangluo 726000， Shaanxi，China）

The direct differential method for solving equations of heat conduction and simulate the casting process of magnesium alloy. The effect of the mould on distribution of temperature and the casting quality is studied. The results show that during the sand mold casting， due to coeffcient of conduction for mould is small， the solidification velocity of cast is slowly， the mutation of temperature in the interface of cast/mold is small. During the metal mold casting， due to coeffcient of conduction for mould is larger， the solidifcation velocity of cast is fast， the mutation of temperature in the interface of cast/mold is larger. In the actual casting process， we should choose the material with suitable thermal coeffcient conductivity to make mold， to avoid larger thermal deformation and cracking phenomenon while improve the casting speed.

Magnesium alloy； Casting process； Temperature distribution； Mould

TG244+.1;

A；

1006-9658（2015）04-0050-04

10.3969/j.issn.1006-9658.2015.04.014

商洛学院第六届大学生创新实践项目(15slcx132); 2015年陕西省大学生创新训练项目(2268)；陕西省教育厅专项科研计划资助项目(14JK1223); 陕西省教育科学“十二五”规划资助项目(SGH13401)

2015-03-02

稿件编号:1503-833

胡瑞霞(1993—), 女, 主要从事凝固过程微观组织形成的研究; 通讯作者：袁训锋(1984—), 男, 博士. 主要从事凝固过程微观组织形成的研究.