数控龙门铣床整机动态特性分析*
2015-10-31黄美发韦礼凯林振广李学聪
伍 伟,黄美发,韦礼凯,林振广,李学聪
(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;2.桂林机床股份有限公司 研发部,广西 桂林 541004)
数控龙门铣床整机动态特性分析*
伍伟1,黄美发1,韦礼凯2,林振广2,李学聪2
(1.桂林电子科技大学 机电工程学院,广西 桂林541004;2.桂林机床股份有限公司 研发部,广西 桂林541004)
某公司数控龙门铣床是采用经验设计,没有考虑到动态特性对整机加工的影响,而铣床的动态性能对零件的加工质量有重要影响。采用有限元分析软件ANSYS Workbench建立了整机的有限元模型,对龙门铣床进行模态分析,得到了前六阶固有频率和振型,发现第一阶固有频率较低,容易发生共振。并对龙门铣床进行了谐响应分析,获得动态切削力下刀具的振动响应,找到整机动态特性的薄弱环节,为结构改进提供理论依据。
数控龙门铣床;有限元;模态分析;谐响应分析
0 引言
随着我国经济的快速发展与科学的进步,数控机床作为新一代工作母机,被广泛应用于汽车、模具、航天、军工等机械领域[1]。精密加工技术的迅速发展和零件加工精度的不断提高对数控机床的精度也提出了更高的要求,因此对整机结构的动态性能有更高的要求。而数控机床在加工过程中,受到切削力以及机床内部不平衡旋转部件产生的激振力的作用,将会使机床产生振动,严重影响到工件的加工质量、刀具寿命和生产效率[2-4]。而目前大部分企业对机床的设计仍采用经验类比的方法,设计时只考虑了机床的静态特性,对机床的动态特性考虑的较少。因此对机床进行动态特性分析是很有必要的[5]。
本文利用有限元分析软件ANSYS Workbench建立了数控龙门铣床有限元模型,并进行了动态特性分析。通过模态分析和谐响应分析,得到数控龙门铣床的固有频率和振型,以及在实际切削作用下的动态响应,发现该铣床薄弱的共振频率,为结构优化改进提供理论支持。
1 铣床实体模型及有限元模型建立
1.1数控龙门铣床实体模型
某企业自主研发的数控龙门铣床,该铣床主要由左右两个立柱、横梁、滑枕、滑鞍、床身、工作台等组成。如图1所示为数控龙门铣床的三维装配图。在实体建模及装配过程中,对各个部件实际结构进行了适当的简化,将倒角、圆角简化成直角,忽略螺纹孔、键槽、退刀槽、去除了螺栓、螺母等零件。简化的模型不会影响到整机的刚度和强度,但可以提高计算效率[6]。
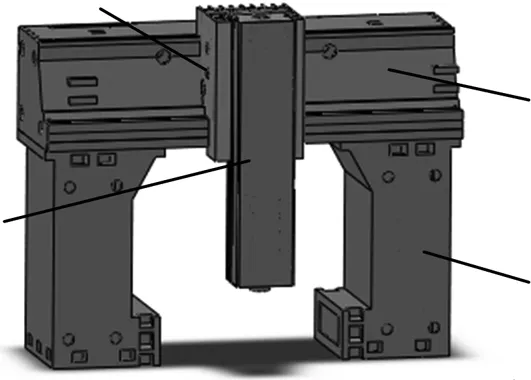
1.立柱 2.横梁 3.滑鞍 4.滑枕
1.2数控龙门铣床有限元模型
将三维实体模型导入到有限元分析软件ANSYS Workbench中,设置各个部件的材料属性,其中,立柱的材料是HT200,其密度是7200kg/m3,杨氏模量是1.48×1011Pa,泊松比是0.31。横梁、滑枕和滑鞍的材料是HT300,其密度是7300kg/m3,杨氏模量是1.43×1011Pa,泊松比是0.27。
接触面按照实际情况进行设置,对滑块导轨结合面采用No Separation不分离接触的接触单元,模仿滚动结合面。对螺栓结合面采用Bonded绑定接触的接触单元,模仿固定结合面[7]。
网格划分质量会对模型的计算精度产生较大影响,而ANSYS Workbench具有强大的自动划分网格的能力,因此采用自动网格划分功能进行网格划分,综合考虑到计算精度和计算时间,在mesh中进行网格划分参数的设置,将Relevance Center设置为“Fine”,Smoothing设置为“High”,Span Angle Center设置为“medium”,其他默认不变。划分后数控龙门铣床的节点数为325813个,单元数为177360个。
立柱的底部与地面是用螺栓连接,内侧面是与床身用螺栓连接,在这两个面施加固定约束。建立的有限元模型如图2所示。

图2 有限元模型
2 模态分析
2.1有限元模态分析的原理
对于一般多自由度的结构来说,任何运动都可以由其自由振动的模态来合成。有限元的模态分析就是建立相应的模态模型并进行数值计算过程[8]。
模态分析的实质是求解具有有限个自由度的无阻尼及无外载荷状态下的运动方程的模态矢量[9]。结构阻尼对模态频率和振型影响很小,可以忽略,因此求解振动频率与振型的矩阵表达式为:
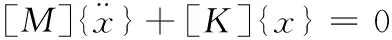
(1)
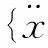
在系统自由振动中,假设所有质量均作简谐振动,则方程解的形式为:
{xi}={Ai}sin(wit+φi)
(2)
式中,wi、φi分别为第i阶振型的固有频率和相角;{xi}为第i阶振型的诸位移的列阵;{Ai}为第i阶振型中各点振幅向量。
将(2)带入(1),可以得到:
(3)
由(3)方程可以求得固有频率ωi和其相应的振型{Ai}。
2.2数控龙门铣床模态分析
模态分析的目的是获取整机的固有频率,从而指导实际加工过程中,外界激励远离数控龙门铣床的固有频率,保证零件加工质量。
由于高阶模态固有频率已远高于实际情况所能达到的激振频率,一般不会发生共振,故只提取前6阶固有频率,见表1所示。前6阶振型见图3所示。
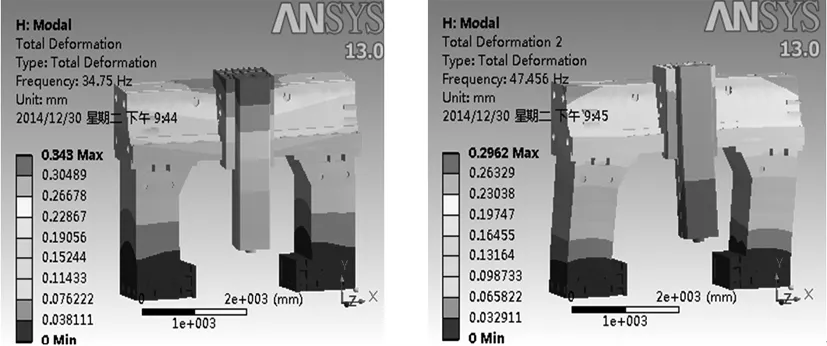
1阶振型 2阶振型

3阶振型 4阶振型

5阶振型 6阶振型

阶数123456频率34.7547.45667.3879.89118.2127.41
由动画显示可以得到,第1阶振型是龙门框架带动滑鞍、滑枕前后摆动,第2阶振型是龙门框架带动滑鞍、滑枕左右摆动,第3阶振型是龙门框架绕y轴扭转,第4阶振型是滑枕前后摆动,第5阶振型是滑鞍和滑枕一起前后摆动,第6阶振型是滑枕的左右摆动。该龙门铣床刀具转速为275r/min,刀具为8齿,由激振频率公式[10]:
式中:fr为激振频率;n为刀具的转速;z为刀具齿数。
计算可得,加工时铣床受到切削激振频率为36.7Hz,与铣床最小固有频率34.75Hz接近,容易激发共振,影响到加工质量。考虑到第一阶振型是龙门框架前后摆动,可以考虑在立柱前后加支撑板或者提高龙门框架前后方向的抗弯刚度。
3 谐响应分析
模态分析可以得到整机的各阶频率和振型,所得到的振型幅值并不是其真实幅值,而是表示铣床各部件的相对振动情况,而外力激励下各阶振型对整机振动作用大小是不同的,还需要对整机进行谐响应分析,研究铣床在动态切削力激振干扰下的抗振性能[11]。
铣床铣削功率P=28kW,电机转速n=1100r/min,常用刀具为8齿直径315mm的刀盘,传动比为1:4,传动效率为0.98,选择切削方式为平面铣。
(1)
(2)
Fx=0.25P,Fy=0.37P,Fz=1.1P
(3)
式中P为铣削功率,n为电机转速,i为传动比,η为传动效率,D为刀盘直径,M为铣削扭矩,F为圆周铣削力, Fx,Fy和Fz分别为x向切削力,y向切削力和z向切削力。
通过公式(1)、(2)、(3)计算得到x、y、z三个方向的切削力分别为1512.7N、2238.6N、6655.3N。将三个方向的力加载到铣刀上,根据模态分析得到的整机的固有频率,设置激振频率范围为0~140Hz,子步数为70,用此简谐力对整机进行激振。得到该激振频率范围下刀具的x、y、z三个方向的谐响应分析的幅频曲线,这是衡量机床动态性能的重要指标,如图4所示。
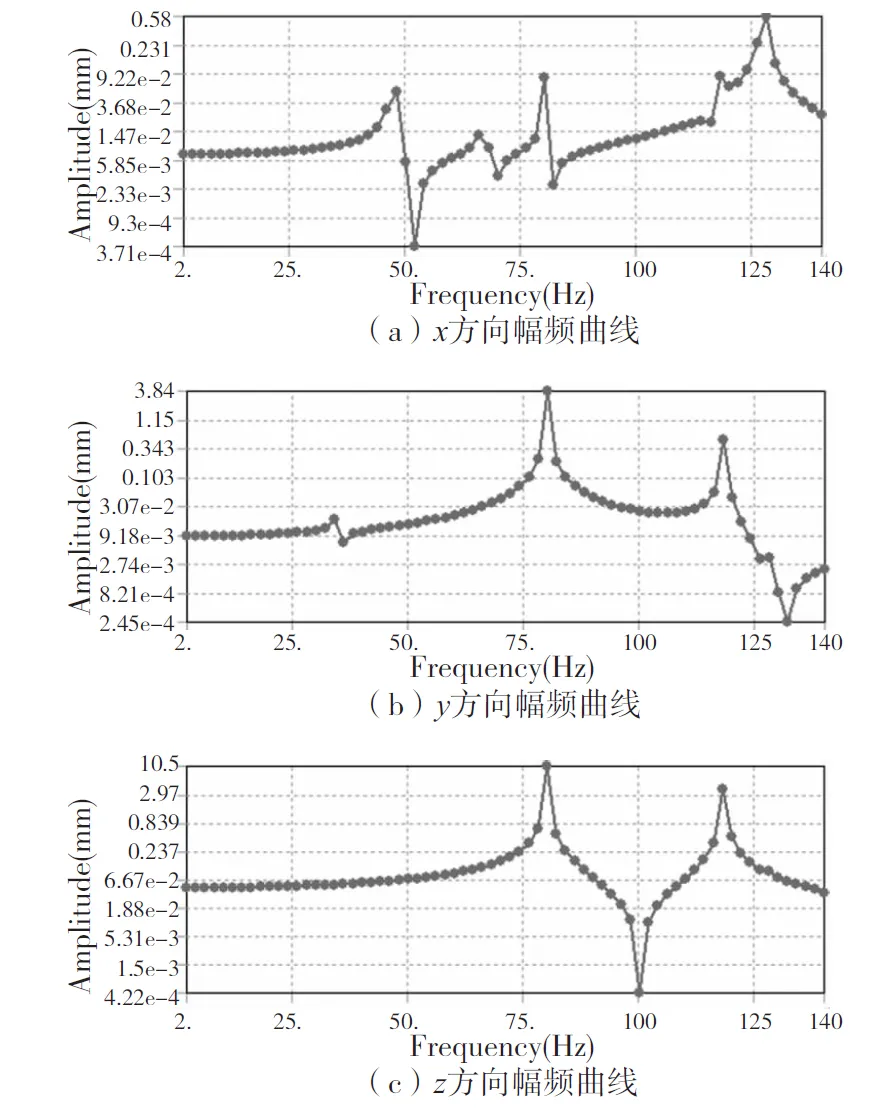
图4 x、y、z三方向的幅频特性曲线图
由刀具的幅频曲线图,可以得到x方向的幅值较大的激振力频率为47.456Hz、79.89Hz、118.2Hz、127.41Hz,y方向的幅值较大的激振力频率为34.75Hz、79.89Hz、118.2Hz,z方向的幅值较大的激振力频率为79.89Hz、118.2Hz。这些频率与模态分析得到的前六阶固有频率基本一致,从而也验证了模态分析结果的准确性。
从图中可以得到各个共振频率下的幅频响应。其中切削力的激振频率在34.75Hz、47.456Hz和79.89Hz时,引起的刀具振动响应在0.01mm级,所以仍然可以满足加工要求。而切削力的激振频率在79.89Hz、118.2Hz和127.41Hz下引起的振动响应分别是10.548mm,4.97mm和0.58mm,即外界激振力频率与铣床的三、五、六阶固有频率接近时,将严重影响铣床加工精度,因此在加工过程中避免外界激励频率在三、五、六阶固有频率附近。
4 结束语
(1)采用有限元软件ANSYS Workbench对数控龙门铣床进行了模态分析。通过模态分析得到了铣床的前6阶固有频率和振型,发现铣床的第1阶固有频率较低,且与外界激励频率较接近,有必要提高1阶固有频率。考虑到1阶振型为龙门框架前后摆动,可以考虑在立柱前后加支撑板或提高龙门框架前后方向的抗弯刚度。
(2)对铣床整机进行谐响应分析,得到了整机在x、y、z三方向的共振频率和峰值,共振峰值最大的频率值即为整机的薄弱的共振频率。
(3)通过对数控龙门铣床整机动态特性的分析,并找到了引起铣床共振的薄弱环节,为工程技术人员进行结构改进设计提供了方向。
[1] 梁铖,刘健群. 五轴联动数控机床技术现状与发展趋势[J]. 机械制造,2010,48(545):5-7.
[2] 何伯吹. 机床设计手册[M]. 北京:机械工业出版社,1979.
[3] 季彬彬,张森,杨玉萍,等. GMF3022龙门加工中心横梁的模态及谐响应分析[J]. 组合机床与自动化加工技术,2013(10):36-38.
[4] 孙峨,蒋书运,马青芬. 高速立式加工中心结构动态设计[J]. 制造技术与机床,2010(6):79-81.
[5] 叶佩青,王仁彻,赵彤,等. 机床整机动静态特性研究进展[J]. 清华大学学报,2012,52(12):1758-1763.
[6] 高东强,毛志云,张功学,等. DVG850工作台静、动态特性分析及结构改进[J]. 机械设计与制造,2011(3):146-147.
[7] 徐先勇,崇凯,严小林,等. 基于ANSYS Workbench的内螺纹磨削中心整机动态特性分析[J]. 组合机床与自动化加工技术,2012(12):23-25.
[8] 闻邦椿,刘树英,陈照波,等. 机械振动理论及应用[M]. 北京:高等教育出版社,2009.
[9] 凌桂龙,丁金滨,温正. ANSYS Workbench 13.0从入门到精通[M]. 北京:清华大学出版社,2012.
[10] 谭亚明. 基于微小型铣床的微细铣削加工试验研究[D]. 哈尔滨:哈尔滨工业大学,2006.
[11] 周军勇,金涛,赵万华,等. 高速数控车削中心动态特性分析及结构优化[J]. 机床与液压,2012,40(3):122-125.
(编辑李秀敏)
Dynamic Performance Analysis of CNC Planer Type Milling Machine
WU Wei1, HUANG Mei-fa1, WEI Li-kai2,LIN Zhen-guang2,LI Xue-cong2
(1.School of Mechanical & Electrical Engineering, Guilin University of Electronic Technology, Guilin Guangxi 541004, China; 2.Research & Development Department, Guilin Machine Tool Co., Ltd, Guilin Guangxi 541004, China)
CNC planer type milling machine in a certain company is designed by using empirical method and without considering the whole machine processing impacts of the dynamic characteristics. And the dynamic performance of the milling machine has important effect on the processing quality of parts. The whole machine finite element model is established by finite element analysis software ANSYS workbench. The first six nature frequencies and modes are obtained by modal analysis, and it is easy to resonate that the first nature frequency is low. The vibration response of cutter under dynamic cutting force is obtained by harmonic response analysis. The weakness link of the whole machine dynamical characteristics is found. It provides the theoretical for the structure improvement.
CNC planer type milling machine; finite element; modal analysis; harmonic analysis
1001-2265(2015)11-0019-03DOI:10.13462/j.cnki.mmtamt.2015.11.006
2015-02-06
国家自然科学基金(51365009);广西科学研究与技术开发计划项(桂科能1355012-5);广西硕士研究生科研创新项(YCSZ2014134)
伍伟(1988—),男,湖南永州人,桂林电子科技大学硕士研究生,研究方向为机床结构优化设计及轻量化,(E-mail)wuwei198812@163.com;黄美发(1962—),男,广西蒙山人,桂林电子科技大学教授,博导,研究方向为数控机床开发及机床精度、新一代GPS理论,(E-mail)hmhmf@guet.edu.cn。
TH166;TG506
A
