一种航空薄壁件铣削加工变形补偿算法
2015-10-31刘建宁李占锋
刘建宁,李占锋,司 宇
(1.烟台职业学院 机械工程系,山东 烟台 264670;2.北京航空航天大学 机械设计及自动化系,北京 100191)
一种航空薄壁件铣削加工变形补偿算法
刘建宁1,2,李占锋2,司宇2
(1.烟台职业学院 机械工程系,山东 烟台264670;2.北京航空航天大学 机械设计及自动化系,北京100191)
采用解析法与数值方法相结合,对铣刀和工件相互耦合作用下的铣削加工变形开展研究,分别获得铣削过程中铣刀与工件的变形量,绘制出薄壁件在不同约束下的加工变形曲线,揭示了在铣削过程中铣刀与工件的加工变形规律,提出高精密薄壁结构加工变形的补偿方案,优化铣削参数,研发铣削加工变形计算系统,提高加工精度和质量,为建立薄壁件铣削参数优化奠定理论基础。
航空薄壁件;铣削加工;误差补偿
0 引言
在航空航天、军工制造业中,为了减轻重量并提高结构强度和使用性能,飞机及发动机等的一些大型结构件通常采用整体结构设计,如整体壁板、整体翼肋和发动机的涡轮叶片等。大型结构件具有形状复杂,刚度弱,精度高等特征,在加工中多采用整体数控铣削成形。然而,在对深腔薄壁件进行高速铣削加工过程中,铣削力极易引起弱刚度薄壁件发生弹性变形,使得实际铣削参数不等于其设定值,出现所谓的“让刀”或“过切”等现象,降低了加工精度,影响了表面质量,甚至造成结构件报废。目前,典型特征结构件的切削工艺技术仍依赖于传统的试切法,即基于经验的工艺参数选择,进行小切削量多步切削加工,这些经验方法成本高、周期长,缺乏可操作性与量化分析,结构件加工质量也不能得到保证。因此,为了有效地控制加工变形,保证结构件加工精度,应开展有效的变形预测、误差补偿与工艺参数优化技术的研究。
近年来,国内外均对加工过程数值模拟技术展开了大量的研究,运用仿真方法对加工变形和表面误差进行计算和模拟[1-3],但目前对大型薄壁结构件铣削加工变形的有限元研究中,往往只单独考虑了工件或铣刀的变形对加工误差的影响,而忽略了加工过程中二者之间的相互变形对加工件精度的影响[4-6]。
本文对影响加工精度的物理量进行建模和分析,以铣刀和工件作为研究的对象,采用数值模拟二者之间的变形量,弥补二者之间相互变形所带来的加工误差。通过提取关键的影响因素,实现关键因素对工艺参数进行优化选取和控制,并提出加工过程的补偿方案,使整个加工过程处于最佳状态。
1建立铣削加工模型
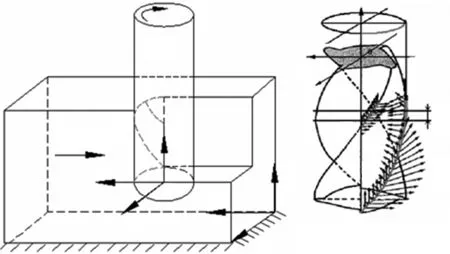
图1 三维铣削力模型
依据图1所示的三维铣削力模型, 在铣刀轴向方向取高度为dz的微元,那么在螺旋微元上的切向、径向和轴向的切削力可由式(1)表示。
(1)
式中:dFt,j(φ,z)、dFr,j(φ,z)和dFa,j(φ,z)分别代表切向力、径向力和轴向力的微元,N;j代表轴向切深积分,设定φ=0处j=0,其余j=1,2,3,…;n代表齿数;φ代表瞬时齿位角,°;z代表沿轴向的距离,mm;Ktc、Krc和Kac分别代表切向、径向和轴向铣削力系数,MPa;hj(φ,z)代表铣厚度,mm;Kte、Kre和Kae分别代表切向、径向和轴向刃口力系数,N·mm-1;dz代表轴向的切深微元,mm。
式(1)中的铣削厚度hj(φ,z):hj(φ,z)=csinφj(z)
式中:c代表进给率,mm/r。
如图2所示,将切向、径向、轴向的三个方向的铣削力在x,y,z轴上投影,并经坐标变换,可得式(2):
(2)
式中:Fx、Fy和Fz分别代表铣削力在x,y,z轴上的分量,N;Ft、Fr和Fa分别代表铣削力沿切向、径向和轴向的分量,N。
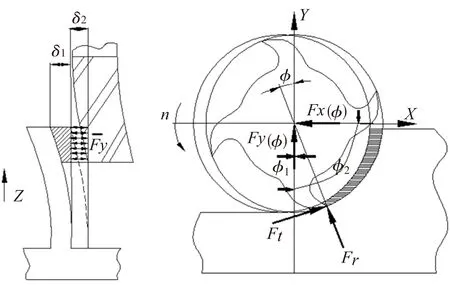
图2 铣刀与工件的变形与切削力
对铣刀沿着铣削刃长度积分后,切入角φ1到切出角φ2切削力为:
(3)
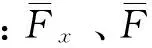
将切入角φ1=0°,切出角φ2=90°代入式(3),由于铣刀的切削刃比较复杂,切向、径向和轴向铣削力系数Ktc、Krc和Kac等求解复杂,故采用快速标定铣刀的实验方法。在固定接触和轴向切深下,改变进给率,并进行一组实验,测量每个刀齿的周期平均力。为了避免测量时刀偏心的影响,先测量主轴每转的总铣削力,再除以刀齿数。若实验测得的力与表达式的铣削力相等,则铣削力系数可以辨识。铣刀周期内切除的材料总量是一定的,平均铣削力与螺旋角无关,因此,各方向的平均铣削力为:
(4)
加工过程中,由于铣削力的作用,铣刀和工件均产生弹性变形。走刀过后弹性变形恢复,致使部分材料残留而未被切除,造成工件表面加工误差。沿被加工面法向的分力是决定工件表面加工误差的主要因素,薄壁件加工的变形主要由Fy产生。
2 建立铣削有限元模型
在有限元建模中,文献[7]将铣刀简化为圆柱体,虽可简化计算过程,但求解精度降低。考虑到铣刀结构的复杂性,本文建立铣刀-工件三维有限元模型时,对铣刀采用四面体单元,工件采用六面体单元划分网格,如图3所示。
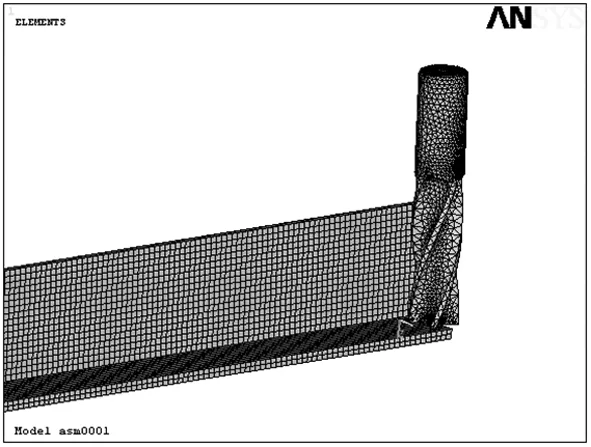
图3 铣刀-工件的有限元模型
3 铣刀与工件加工变形分析
由于铣削力作用,任意加工瞬间工件被加工表面生成点(刀齿螺旋线与工件被加工后形成表面的交点)的变形沿法向投影到被加工表面形成加工误差[8]。采用式(4)计算被加工表面生成点误差δ(i,j):
δ(i,j)=δT(i,j)+δw(i,j)
(5)
式中:δ(i,j)表示被加工表面生成点误差量,mm;δT(i,j)表示该点铣刀的加工点误差量,mm,δw(i,j)表示该点的工件的加工点误差量,mm。
3.1假设条件
铣削过程中造成薄壁件变形的因素较多,如残余应力、装夹应力、铣削热等,本文主要以铣削过程中,以铣削力造成铣刀和工件的变形开展研究。为了提高仿真过程的可靠性,对铣削过程做如下假设:
(1)工件材料为7075铝合金,忽略残余应力对变形的影响;
(2)假设铣刀无限锋利,切屑迅速从工件中脱落,并在加工过程中采用高压空冷,忽略铣削热变形的影响;
(3)忽略装夹变形的影响。
工件参数和加工参数如表1所示。
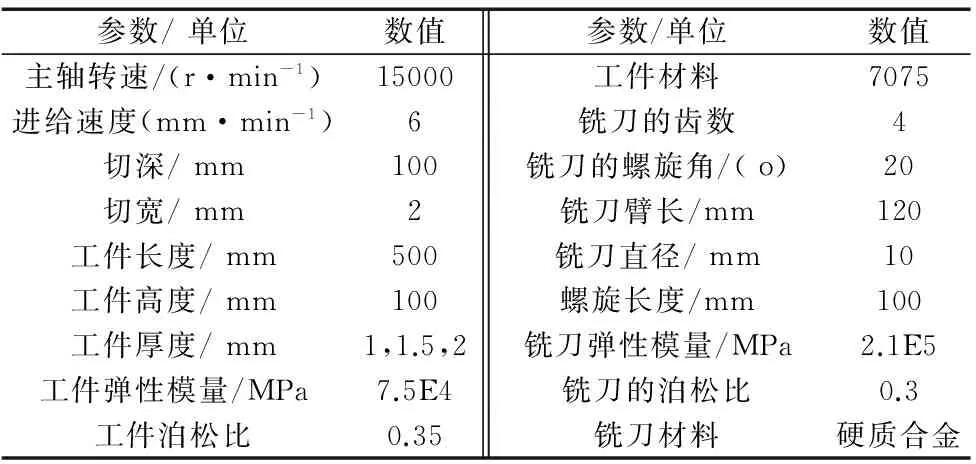
表1 工件参数和加工参数
3.2约束方式
薄壁件简化为三种约束方式:①仅底面约束,②底面和一侧面约束,③三面全部约束,如图4所示。

(a)仅底面约束 (b)底面和侧面约束 (c)三面全部约束
依据三种约束方式,对工件实施位移加载,将铣削力模型源程序,以迭代方式加载到工件侧壁,求解运算。某一瞬间的铣刀与工件的加工变形,如图5所示。
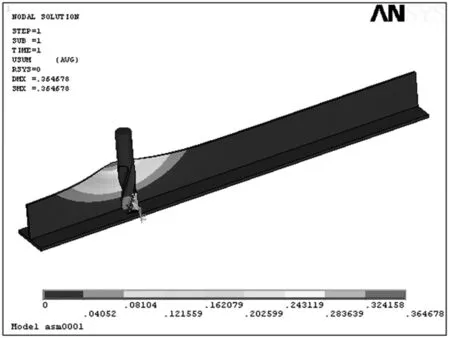
图5 某瞬态下铣刀与工件的仿真变形
不同约束下铣刀与工件的变形值,可从仿真的结果参数提取,并绘制不同约束条件下变形图,如图6所示。
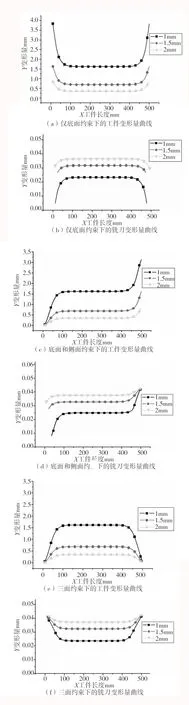
图6 不同约束条件下的变形图
3.3结果分析
分析图6可以得到如下结果:
(1)在铣削过程中,薄壁件厚度对薄壁变形的影响较大。从图6a、6c和6e均可看出,壁厚1mm,1.5mm,2mm时,薄壁的变形分别为1.6 mm,0.7mm,0.25 mm,呈显著降低趋势;从图6b、6d和6f可看出,铣刀变形对加工精度的影响却呈明显增大趋势,铣刀的变形量占加工变形总量的比例分别为1.25%,4.2%,12.5%。
(2)不同约束条件对铣刀与工件的变形均有影响。根据图6各曲线可知,沿着长度方向,在0~100mm开始位置和400~500mm结束位置时,约束条件使铣刀和工件的变形量发生剧增和骤减的现象;而在中间位置200~400mm时,二者变形趋于平稳,保持稳定的变形量。
(3)分别对比图6a和6b、图6c和6d、图6e和6f可知,铣刀与工件的变形量变化恰呈相反的趋势。薄壁件的变形使铣削参数发生了变化,改变了铣削力的大小,当工件的变形最大时,铣刀的变形量最小。同理反之,当工件的变形最小时,铣刀的变形量较大。
4 变形误差补偿方法
为了提高加工精度,结合文献[9]给出的变形控制误差补偿基本原理,依据仿真分析的结果,本文提出采用铣削力数学解析法与有限元变形分析相结合的补偿方法,具体步骤如下:
(1)建立铣削加工系统数学模型,设置加工条件与加工参数;
(2)根据加工条件、加工参数和数学模型,进行仿真,获得铣削力数值;
(3)通过有限元计算,将铣削力不断叠加到薄壁件侧壁和铣刀上,求解加工过程中铣刀与工件的变形量;
(4)通过有限元分析的变形量,确定薄壁件加工形状误差;
(5)进行误差补偿,确定优化铣削参数。进行循环叠加,直到结果满足精度要求,从而确定优化铣削参数;
(6)将优化铣削参数输入数控系统中,进行实际加工过程验证验证。具体的迭代步骤如图7所示。
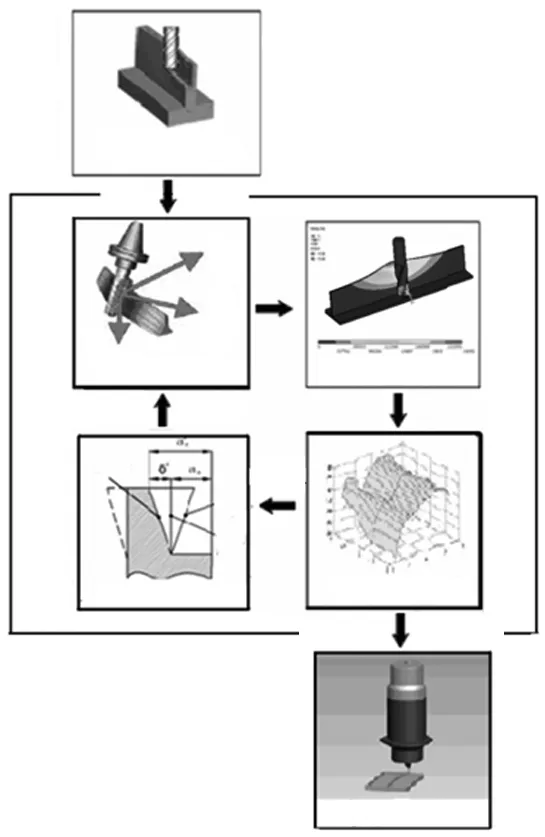
图7 加工系统误差补偿过程
5 铣削加工变形参数计算系统的应用
由于航空结构件具有大型、薄壁、结构复杂等特征,对整个结构进行有限元计算或分析时运算量极大、效率低、分析不方便。文献[10]已提出对应模型关系,即,在复杂薄壁零件加工时,弹性让刀变形主要发生在局部位置,基于整体模型局部特征关系参数化建立与之对应的简化薄壁模型。结合以上铣刀与工件加工变形控制补偿理论与方法,研发出铣削加工变形参数计算系统,具体界面如图8所示,通过输入铣削参数等信息,可快速计算出刀具与工件的加工变形量,计算结果如图9所示。
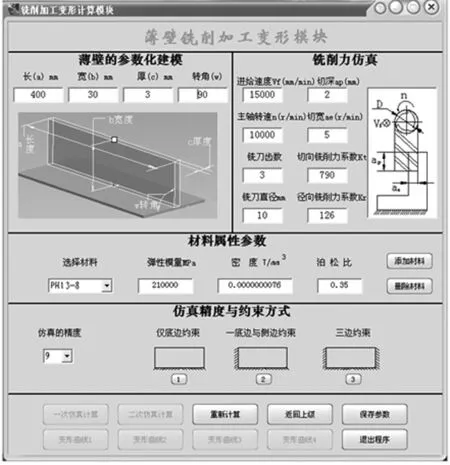
图8 铣削参数输入界面
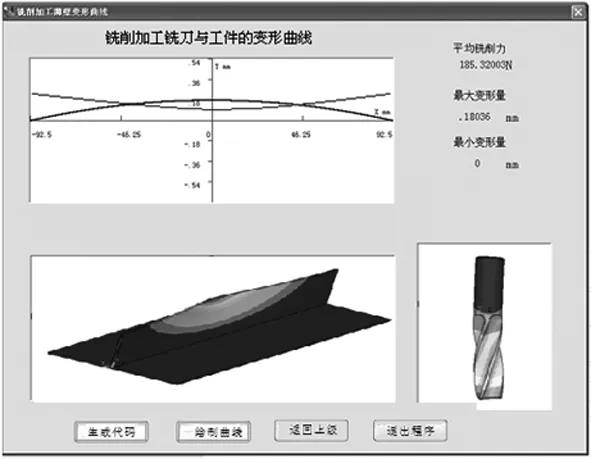
图9 计算变形结果输出界面
根据铣削仿真分析的结果,可直接输出二次插值变形补偿的数控程序代码(程序中逗号仅用以区分程序命令),实现整个铣削加工参数的优化,具体的局部参数优化代码如下:
…
N10,T1,D1;指定10mm立铣刀及刀具参数
N20,G17,G90,G54;调用绝对坐标,调用工件坐标
N30,S7000,M3 ;设定主轴转速,主轴正转
N40, R = DFM1;软件仿真的最大变形量DFM1赋值给R,
N50,G1,G91,Z5,F100 ;Z方向进给加工
N60, G1, G91, XL, YR, F300;第一段插值补偿直线进给加工
N70, G1, G91, XL, Y-R, F300;第二段插值补偿直线进给加工
…
6 结论
(1)本文采用了铣削力数学解析法与有限元法相互结合,分析薄壁结构件加工过程中铣刀与工件的变形量。实现铣削参数优化,减少加工误差,提高加工精度。
(2)根据铣刀与工件的变形曲线分析可知,对具有不同约束和壁厚的工件进行加工时,变形量有较大的差异。但变形曲线有着共同的规律,即:在加工过程的开始与结束时,铣削与工件的变形量随着长度方向呈现非线性的曲线关系。在加工过程的中间部分,变形量趋于稳定。
(3)将铣削力模型、加工变形模型和数控补偿模型集成后,为薄壁结构件的快速加工变形补偿系统提供理论,为铣削参数优化奠定基础。
[1] 陈双喜. 基于ABAQUS的薄壁圆筒零件车削加工变形补偿计算[J]. 组合机床与自动化加工技术, 2008(11):33-35.
[2] 吴琼,张以都,张洪伟,等. 航空薄壁件与铣刀的加工变形误差补偿研究[J] . 武汉理工大学学报, 2008, 30(9):116-119.
[3] 杜敏娟,李昊. 基于误差补偿的叶片铣削加工过程仿真研究[J]. 制造技术与机床, 2012(3):13-18.
[4] 黄泽华. 整体叶轮铣削加工弹性变形预测及误差补偿研究[D].北京:北京交通大学, 2013.
[5] 郭宏杰,孙敬阳,王晓枫, 等. 机床加工中的精度补偿技术[J].组合机床与自动化加工技术, 2014(5):133-134.
[6] Wang M, Sun Y. Error prediction and compensation based on interference-free tool paths in blade milling[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(5-8):1309-1318.
[7] 代军,汤立民,张以都,等. 航空薄壁件加工变形与动态特性分析[J] . 机械设计与制造, 2011(3):182-184.
[8] Wukai, Hening. The Application of the Thin-wall FEM Technology on the Deformation Analysis of the Work Piece Milling in Aerospace Industries [J].Journal of applied sciences.2003,21 (1):68-71.
[9] 吴琼. 飞机零件中典型结构的加工变形与动态特性研究[D].北京:北京航空航天大学, 2009.
[10] 张晓峰,周凯,陆俊百.基于B样条的航空薄壁件加工变形预测与控制[J]. 机械科学与技术, 2010, 27(4):44-46.
(编辑李秀敏)
A Method of Machining Deformation Compensation for Aeronautical Thin-walled Parts
LIU Jian-ning1,2,LI Zhan-feng2,SI Yu1
(1. Department of Mechanical Engineering,Yantai Vocational College, Yantai Shandong 264670, China;2.School of Mechanical Engineering and Automation,Beihang University ,Beijing 100191, China)
Based on combination between analytical method and numerical method, research on deformation of tools and work pieces is performed; The curve about deformation of tool and work piece is obtained in the different constraints. The factors and law about machining deformation is explored in the cutting process. Provide an error compensation scheme for thin-walled parts machining deformation. This scheme will optimize parameters of milling and improve accuracy and efficiency of milling. The computing system of milling deformation is developed. It is established basis for parametric optimization in thin-walled cutting process.
aeronautical thin-walled parts; milling machining;error compensation
1001-2265(2015)11-0033-04DOI:10.13462/j.cnki.mmtamt.2015.11.010
2014-12-15;
2015-03-16
刘建宁(1959—),男,山东蓬莱人,烟台职业学院教授,研究方向为机械制造,(E-mail)ljn_6666@126.com。
TH162;TG506
A
